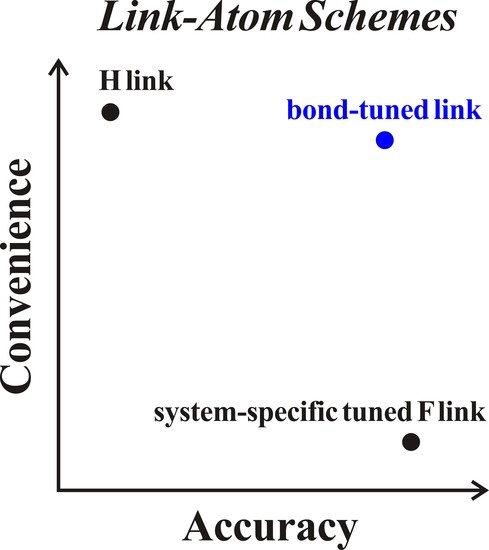
Parametrization of Combined Quantum Mechanical and Molecular Mechanical Methods: Bond-Tuned Link Atoms
Abstract
:1. Introduction
2. Method
3. Details of the Validation Calculations
4. Results and Discussion
4.1. Tuning Parameters
4.2. CM5 Charge Analyses
4.3. Deprotonation Energies
5. Concluding Remarks
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Gao, J.; Thompson, M.A. (Eds.) Combined Quantum Mechanical and Molecular Mechanical Methods; ACS Symposium Series 712; American Chemical Society: Washington, DC, USA, 1998. [Google Scholar]
- Sherwood, P. Modern Methods and Algorithms of Quantum Chemistry; Grotendorst, J., Ed.; John von Neumann Institute for Computing: Jülich, Germany, 2000; p. 285. [Google Scholar]
- Lin, H.; Truhlar, D.G. QM/MM: What have we learned, where are we, and where do we go from here? Theor. Chem. Acc. 2007, 117, 185–199. [Google Scholar] [CrossRef]
- Senn, H.M.; Thiel, W. QM/MM methods for biomolecular systems. Angew. Chem. Int. Ed. 2009, 48, 1198–1229. [Google Scholar] [CrossRef] [PubMed]
- Bernstein, N.; Kermode, J.R.; Csányi, G. Hybrid atomistic simulation methods for materials systems. Rep. Prog. Phys. 2009, 72, 026501. [Google Scholar] [CrossRef]
- Brunk, E.; Rothlisberger, U. Mixed quantum mechanical/molecular mechanical molecular dynamics simulations of biological systems in ground and electronically excited states. Chem. Rev. 2015, 115, 6217–6263. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.; Truhlar, D.G. Quantum mechanical methods for enzyme kinetics. Annu. Rev. Phys. Chem. 2002, 53, 467–505. [Google Scholar] [CrossRef] [PubMed]
- Nam, K.; Gao, J.; York, D.M. Quantum mechanical/molecular mechanical simulation study of the mechanism of hairpin ribozyme catalysis. J. Am. Chem. Soc. 2008, 130, 4680–4691. [Google Scholar] [CrossRef] [PubMed]
- Lundberg, M.; Kawatsu, T.; Vreven, T.; Frisch, M.J.; Morokuma, K. Transition states in a protein environment—ONIOM QM:MM modeling of isopenicillin N synthesis. J. Chem. Theory Comput. 2009, 5, 222–234. [Google Scholar] [CrossRef] [PubMed]
- Rosta, E.; Woodcock, H.L.; Brooks, B.R.; Hummer, G. Artificial reaction coordinate ‘‘tunneling’’ in free-energy calculations: The catalytic reaction of RNase H. J. Comput. Chem. 2009, 30, 1634–1641. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Yang, W. Development and application of ab initio QM/MM methods for mechanistic simulation of reactions in solution and in enzymes. J. Mol. Struct. Theochem. 2009, 898, 17–30. [Google Scholar] [CrossRef] [PubMed]
- Shaik, S.; Cohen, S.; Wang, Y.; Chen, H.; Kumar, D.; Thiel, W. P450 enzymes: Their structure, reactivity, and selectivity—Modeled by QM/MM calculations. Chem. Rev. 2010, 110, 949–1017. [Google Scholar] [CrossRef] [PubMed]
- Lonsdale, R.; Harvey, J.N.; Mulholland, A.J. Compound I reactivity defines alkene oxidation selectivity in cytochrome P450cam. J. Phys. Chem. B 2010, 114, 1156–1162. [Google Scholar] [CrossRef] [PubMed]
- Kanaan, N.; Ferrer, S.; Martí, S.; Garcia-Viloca, M.; Kohen, A.; Moliner, V. Temperature dependence of the kinetic isotope effects in thymidylate synthase: A theoretical study. J. Am. Chem. Soc. 2011, 133, 6692–6702. [Google Scholar] [CrossRef] [PubMed]
- Hou, G.; Cui, Q. QM/MM analysis suggests that alkaline phosphatase (AP) and nucleotide pyrophosphatase/phosphodiesterase slightly tighten the transition state for phosphate diester hydrolysis relative to solution: Implication for catalytic promiscuity in the AP superfamily. J. Am. Chem. Soc. 2012, 134, 229–246. [Google Scholar] [CrossRef] [PubMed]
- Layfield, J.P.; Hammes-Schiffer, S. Calculation of vibrational shifts of nitrile probes in the active site of ketosteroid isomerase upon ligand binding. J. Am. Chem. Soc. 2013, 135, 717–725. [Google Scholar] [CrossRef] [PubMed]
- Gómez, H.; Rojas, R.; Patel, D.; Tabak, L.A.; Lluch, J.M.; Masgrau, L. A computational and experimental study of O-glycosylation. catalysis by human UDP-GalNAc polypeptide:GalNAc transferase-T2. Org. Biomol. Chem. 2014, 12, 2645–2655. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Li, M.; Chen, N.; Wang, S.; Luo, H.-B.; Zhang, Y.; Wu, R. Computational design of a time-dependent histone deacetylase 2 selective inhibitor. ACS Chem. Biol. 2015, 10, 687–692. [Google Scholar] [CrossRef] [PubMed]
- Luk, L.Y.P.; Ruiz-Pernía, J.J.; Adesina, A.S.; Loveridge, E.J.; Tuñõn, I.; Moliner, V.; Allemann, R.K. Chemical ligation and isotope labeling to locate dynamic effects during catalysis by dihydrofolate reductase. Angew. Chem. Int. Ed. 2015, 54, 9016–9020. [Google Scholar] [CrossRef] [PubMed]
- Quesne, M.G.; Borowski, T.; De Visser, S.P. Quantum mechanics/molecular mechanics modeling of enzymatic processes: Caveats and breakthroughs. Chem. Eur. J. 2016, 22, 2562–2581. [Google Scholar] [CrossRef] [PubMed]
- Sousa, S.F.; Ribeiro, A.J.M.; Neves, R.P.P.; Brás, N.F.; Cerqueira, N.M.; Fernandes, P.A.; Ramos, M.J. Application of quantum mechanics/molecular mechanics methods in the study of enzymatic reaction mechanisms. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2017, 7, e1281. [Google Scholar] [CrossRef]
- Wang, B.; Johnston, E.M.; Li, P.; Shaik, S.; Davies, G.J.; Walton, P.H.; Rovira, C. QM/MM studies into the H2O2-dependent activity of lytic polysaccharide monooxygenases: Evidence for the formation of a caged hydroxyl radical intermediate. ACS Catal. 2018, 8, 1346–1351. [Google Scholar] [CrossRef]
- Choomwattana, S.; Maihom, T.; Khongpracha, P.; Probst, M.; Limtrakul, J. Structures and mechanisms of the carbonyl-ene reaction between MOF-11 encapsulated formaldehyde and propylene: An ONIOM study. J. Phys. Chem. C 2008, 112, 10855–10861. [Google Scholar] [CrossRef]
- Oxford, G.A.E.; Snurr, R.Q.; Broadbelt, L.J. Hybrid quantum mechanics/molecular mechanics investigation of (salen)Mn for use in metal−organic frameworks. Ind. Eng. Chem. Res. 2010, 49, 10965–10973. [Google Scholar] [CrossRef]
- Zheng, M.; Liu, Y.; Wang, C.; Liu, S.; Lin, W. Cavity-induced enantioselectivity reversal in a chiral metal-organic framework Brønsted acid catalyst. Chem. Sci. 2012, 3, 2623–2627. [Google Scholar] [CrossRef]
- Yu, D.; Yazaydin, A.O.; Lane, J.R.; Dietzel, P.D.C.; Snurr, R.Q. A combined experimental and quantum chemical study of CO2 adsorption in the metal-organic framework CPO-27 with different metals. Chem. Sci. 2013, 4, 3544–3556. [Google Scholar] [CrossRef]
- Hirao, H.; Ng, W.K.H.; Moeljadi, A.M.P.; Bureekaew, S. Multiscale model for a metal–organic framework: High-spin rebound mechanism in the reaction of the oxoiron(IV) species of Fe-MOF-74. ACS Catal. 2015, 5, 3287–3291. [Google Scholar] [CrossRef]
- Moeljadi, A.M.P.; Schmid, R.; Hirao, H. Dioxygen binding to Fe-MOF-74: Microscopic insights from periodic QM/MM calculations. Can. J. Chem. 2016, 94, 1144–1150. [Google Scholar] [CrossRef]
- Doitomi, K.; Xu, K.; Hirao, H. The mechanism of an asymmetric ring-opening reaction of epoxide with amine catalyzed by a metal-organic framework: Insights from combined quantum mechanics and molecular mechanics calculations. Dalton Trans. 2017, 46, 3470–3481. [Google Scholar] [CrossRef] [PubMed]
- Doitomi, K.; Hirao, H. Hybrid computational approaches for deriving quantum mechanical insights into metal–organic frameworks. Tetrahedron Lett. 2017, 58, 2309–2317. [Google Scholar] [CrossRef]
- Wu, X.-P.; Gagliardi, L.; Truhlar, D.G. Combined quantum mechanical and molecular mechanical method for metal–organic frameworks: Proton topologies of NU-1000. Phys. Chem. Chem. Phys. 2018, 20, 1778–1786. [Google Scholar] [CrossRef] [PubMed]
- Singh, U.C.; Kollman, P.A. A combined ab initio quantum mechanical and molecular mechanical method for carrying out simulations on complex molecular systems: Applications to the CH3Cl + Cl− exchange reaction and gas phase protonation of polyethers. J. Comput. Chem. 1986, 7, 718–730. [Google Scholar] [CrossRef]
- Koga, N.; Morokuma, K. A simple scheme of estimating substitution or substituent effects in the ab initio MO method based on the shift operator. Chem. Phys. Lett. 1990, 172, 243–248. [Google Scholar] [CrossRef]
- Bakowies, D.; Thiel, W. Hybrid models for combined quantum mechanical and molecular mechanical approaches. J. Phys. Chem. 1996, 100, 10580–10594. [Google Scholar] [CrossRef]
- Zhang, Y.; Lee, T.-S.; Yang, W. A pseudobond approach to combining quantum mechanical and molecular mechanical methods. J. Chem. Phys. 1999, 110, 46–54. [Google Scholar] [CrossRef]
- Antes, I.; Thiel, W. Adjusted connection atoms for combined quantum mechanical and molecular mechanical methods. J. Phys. Chem. A 1999, 103, 9290–9295. [Google Scholar] [CrossRef]
- Alary, F.; Poteau, R.; Heully, J.-L.; Barthelat, J.-C.; Daudey, J.-P. A new method for modelling spectator chemical groups in ab initio calculations: Effective group potentials. Theor. Chem. Acc. 2000, 104, 174–178. [Google Scholar] [CrossRef]
- DiLabio, G.A.; Hurley, M.M.; Christiansen, P.A. Simple one-electron quantum capping potentials for use in hybrid QM/MM studies of biological molecules. J. Chem. Phys. 2002, 116, 9578–9584. [Google Scholar] [CrossRef]
- Dumont, E.; Chaquin, P. The H* method: Hydrogen atoms with a fictitious nuclear charge: A versatile theoretical tool for study of atom and group properties as substituents: Electronegativity and partition of σ and π contributions. J. Mol. Struct. THEOCHEM 2004, 680, 99–106. [Google Scholar] [CrossRef]
- Von Lilienfeld, O.A.; Tavernelli, I.; Rothlisberger, U.; Sebastiani, D. Variational optimization of effective atom centered potentials for molecular properties. J. Chem. Phys. 2005, 122, 014113. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dumont, E.; Chaquin, P. Diels-Alder reaction: A theoretical comprehensive study of substituent effects using the ‘H* method’. J. Mol. Struct. THEOCHEM 2006, 758, 161–167. [Google Scholar] [CrossRef]
- Dumont, E.; Chaquin, P. Investigation of pure inductive effects on benzene ring by 13C NMR chemical shifts: A theoretical study using fictitious nuclear charges of hydrogen atoms (‘H* method’). Chem. Phys. Lett. 2007, 435, 354–357. [Google Scholar] [CrossRef]
- Ohnishi, Y.Y.; Nakao, Y.; Sato, H.; Sakaki, S. Frontier orbital consistent quantum capping potential (FOC-QCP) for bulky ligand of transition metal complexes. J. Phys. Chem. A 2008, 112, 1946–1955. [Google Scholar] [CrossRef] [PubMed]
- Lewin, J.L.; Cramer, C.J. Modified carbon pseudopotential for use in ONIOM calculations of alkyl-substituted metallocenes. J. Phys. Chem. A 2008, 112, 12754–12760. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Truhlar, D.G. Combined quantum mechanical and molecular mechanical methods for calculating potential energy surfaces: Tuned and balanced redistributed-charge algorithm. J. Chem. Theory Comput. 2010, 6, 359–369. [Google Scholar] [CrossRef] [PubMed]
- Théry, V.; Rinaldi, D.; Rivail, J.L.; Maigret, B.; Ferenczy, G.G. Quantum mechanical computations on very large molecular systems: The local self-consistent field method. J. Comput. Chem. 1994, 15, 269–282. [Google Scholar] [CrossRef]
- Gao, J.; Amara, P.; Alhambra, C.; Field, M.J. A generalized hybrid orbital (GHO) method for the treatment of boundary atoms in combined QM/MM calculations. J. Phys. Chem. A 1998, 102, 4714–4721. [Google Scholar] [CrossRef]
- Pu, J.; Gao, J.; Truhlar, D.G. Generalized hybrid orbital (GHO) method for combining ab initio Hartree−Fock wave functions with molecular mechanics. J. Phys. Chem. A 2004, 108, 632–650. [Google Scholar] [CrossRef]
- Monari, A.; Rivail, J.-L.; Assfeld, X. Theoretical modeling of large molecular systems. Advances in the local self consistent field method for mixed quantum mechanics/molecular mechanics calculations. Acc. Chem. Res. 2013, 46, 596–603. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Truhlar, D.G. Geometry optimization using tuned and balanced redistributed charge schemes for combined quantum mechanical and molecular mechanical calculations. Phys. Chem. Chem. Phys. 2011, 13, 10556–10564. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Truhlar, D.G. Tuned and balanced redistributed charge scheme for combined quantum mechanical and molecular mechanical (QM/MM) methods and fragment methods: Tuning based on the CM5 charge model. J. Chem. Theory Comput. 2013, 9, 1036–1042. [Google Scholar] [CrossRef] [PubMed]
- Pacios, L.F.; Christiansen, P.A. Ab initio relativistic effective potentials with spin-orbit operators. I. Li through Ar. J. Chem. Phys. 1985, 82, 2664–2671. [Google Scholar] [CrossRef]
- Antes, I.; Thiel, W. On the treatment of link atoms in hybrid methods. ACS Symp. Ser. 1998, 712, 50–65. [Google Scholar]
- Marenich, A.V.; Jerome, S.V.; Cramer, C.J.; Truhlar, D.G. Charge model 5: An extension of Hirshfeld population analysis for the accurate description of molecular interactions in gaseous and condensed phases. J. Chem. Theory Comput. 2012, 8, 527–541. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Truhlar, D.G. Redistributed charge and dipole schemes for combined quantum mechanical and molecular mechanical calculations. J. Phys. Chem. A 2005, 109, 3991–4004. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Zhang, Y.; Pezeshki, S.; Duster, A.W.; Wang, B.; Wu, X.-P.; Gagliardi, L.; Truhlar, D.G. QMMM 2017; University of Minnesota: Minneapolis, MN, USA, 2017. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Ponder, J.W. TINKER, Version 6.3; Washington University: St. Louis, MO, USA, 2014. [Google Scholar]
- Zhao, Y.; Truhlar, D.G. Density functionals with broad applicability in chemistry. Acc. Chem. Res. 2008, 41, 157–167. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Hehre, W.J.; Random, L.; Schleyer, P.v.R.; Pople, J.A. Ab Initio Molecular Orbital Theory; Wiley: New York, NY, USA, 1986. [Google Scholar]
- Halgren, T.A. Merck molecular force field. I. Basis, form, scope, parameterization, and performance of MMFF94. J. Comput. Chem. 1996, 17, 490–519. [Google Scholar] [CrossRef]
Sample Availability: Samples of the compounds are not available from the authors. |


| Cut bond | C−O | C−N | C−C | N−C | O−C |
| Molecule | H3C−OH | H3C−NH2 | H3C−CH3 | H2N−CH3 | HO−CH3 |
| Cut bond | C−S | S−S | S−C | C−Si | O−N |
| Molecule | H3C−SH | HS−SH | HS−CH3 | H3C−SiH3 | HO−NH2 |
| Bond | C−H | N−H | O−H | S−H |
| Distance | 1.09 | 1.01 | 0.95 | 1.34 |
| Bond | C−F* | N−F* | O−F* | S−F* |
| Distance | 1.33 | 1.41 | 1.41 | 1.65 |
| System-Specific | Bond-Tuned | |
|---|---|---|
| CO_1 | −0.0185 | 0.2256 |
| CO_2 | 0.2075 | 0.2256 |
| CO_3 | 0.2434 | 0.2256 |
| CO_4 | −0.0310 | 0.2256 |
| CO_5 | 0.1954 | 0.2256 |
| CO_6 | −0.2124 | 0.2256 |
| CO_7 | −0.2283 | 0.2256 |
| CO_8 | −0.2392 | 0.2256 |
| CN_1 | −0.0122 | 0.3181 |
| CC_1 | 0.6806 | 0.8463 |
| CC_2 | 0.7715 | 0.8463 |
| CC_3 | 0.7315 | 0.8463 |
| CC_4 | 0.5499 | 0.8463 |
| NC_1 | 1.0798 | 1.0966 |
| OC_1 | 0.8599 | 1.0625 |
| CS_1 | 0.6079 | 0.5888 |
| SS_1 | 0.8256 | 0.8108 |
| SC_1 | 0.9750 | 1.0658 |
| CSi_1 | 0.7520 | 0.9001 |
| ON_1 | 0.5766 | 0.6321 |
| Entire System | Capped QM Subsystem | Deviations | |||
|---|---|---|---|---|---|
| H Link | Bond-Tuned Link | H Link | Bond-Tuned Link | ||
| CO_1 | 0.185 | −0.083 | 0.130 | −0.27 | −0.06 |
| CO_2 | 0.131 | −0.085 | 0.127 | −0.22 | 0.00 |
| CO_3 | 0.107 | −0.103 | 0.111 | −0.21 | 0.00 |
| CO_4 | 0.189 | −0.084 | 0.131 | −0.27 | −0.06 |
| CO_5 | 0.078 | −0.122 | 0.071 | −0.20 | −0.01 |
| CO_6 | 0.229 | −0.082 | 0.131 | −0.31 | −0.10 |
| CO_7 | 0.233 | −0.083 | 0.132 | −0.32 | −0.10 |
| CO_8 | 0.238 | −0.080 | 0.135 | −0.32 | −0.10 |
| CN_1 | 0.157 | −0.112 | 0.081 | −0.27 | −0.08 |
| CC_1 | −0.003 | −0.112 | −0.043 | −0.11 | −0.04 |
| CC_2 | 0.003 | −0.085 | −0.014 | −0.09 | −0.02 |
| CC_3 | 0.000 | −0.102 | −0.027 | −0.10 | −0.03 |
| CC_4 | 0.054 | −0.085 | −0.015 | −0.14 | −0.07 |
| NC_1 | −0.154 | −0.304 | −0.158 | −0.15 | 0.00 |
| OC_1 | −0.109 | −0.342 | −0.157 | −0.23 | −0.05 |
| CS_1 | 0.041 | −0.084 | 0.046 | −0.13 | 0.01 |
| SS_1 | −0.009 | −0.120 | −0.006 | −0.11 | 0.00 |
| SC_1 | −0.049 | −0.120 | −0.073 | −0.07 | −0.02 |
| CSi_1 | 0.007 | −0.086 | −0.028 | −0.09 | −0.04 |
| ON_1 | −0.041 | −0.340 | −0.055 | −0.30 | −0.01 |
| average | −0.20 | −0.04 | |||
| Molecule 1 | DE | H Link | System-Specific Tuned F Link | Bond-Tuned Link | ||||
|---|---|---|---|---|---|---|---|---|
| BRC2 | BSRC | BRC2 | BSRC | BRC2 | BSRC | |||
| CO_1 | HOCH2CH2−OC(O)CH3 | 393.7 | 11.4 | 11.6 | 2.9 | 3.1 | 4.1 | 4.3 |
| CO_2 | HOCH2CH2−OCH2NH2 | 399.6 | 8.4 | 9.4 | 0.6 | 1.7 | 0.7 | 1.8 |
| CO_3 | HOOCCH2−OCHOHCH3 | 365.8 | 5.0 | 6.6 | −1.0 | 0.6 | −1.0 | 0.5 |
| CO_4 | HOCH2CH2CH2−OC(O)CH3 | 396.8 | 7.3 | 7.4 | 1.6 | 1.8 | 2.4 | 2.6 |
| CO_5 | HOCF2CF2−OC(O)CH3 | 356.7 | 6.3 | 7.2 | −0.1 | 0.9 | 0.1 | 1.1 |
| CO_6 | HOCH2CH2−OC(O)CF3 | 385.6 | 12.5 | 12.4 | 4.0 | 3.8 | 6.1 | 5.9 |
| CO_7 | HOCH2CH2CH2−OC(O)CF3 | 391.0 | 8.2 | 8.1 | 2.4 | 2.2 | 3.7 | 3.6 |
| CO_8 | HOCH2CH2CH2CH2−OC(O)CF3 | 393.4 | 6.1 | 6.0 | 1.4 | 1.2 | 2.4 | 2.2 |
| CN_1 | HOOCCH2−NHCOCH3 | 354.7 | 9.0 | 9.4 | −1.1 | −0.5 | 0.6 | 1.1 |
| CC_1 | HOOCCH2−CH2F | 360.8 | 4.6 | 4.7 | −1.9 | −1.8 | −0.9 | −0.9 |
| CC_2 | HOCH2CH2−CHNH2CONH2 | 404.2 | 6.2 | 6.2 | 0.3 | 0.3 | 0.8 | 0.7 |
| CC_3 | HOCH2−CH2OH | 400.8 | 14.7 | 14.8 | 1.8 | 2.0 | 2.9 | 3.0 |
| CC_4 | HOCH2CH2−CH2OC(O)CF3 | 391.0 | 5.7 | 5.6 | −0.9 | −1.0 | 0.6 | 0.6 |
| NC_1 | HOOCCH2NH−CH2CH2OH | 375.3 | 3.3 | 4.2 | −3.4 | −3.0 | −3.3 | −2.9 |
| OC_1 | HOCH2CH2O−CH2CONH2 | 397.8 | 3.6 | 4.0 | −7.1 | −7.0 | −5.7 | −5.6 |
| CS_1 | HOCH2CH2−SCH3 | 393.7 | 12.8 | 13.4 | 6.4 | 7.0 | 6.3 | 6.9 |
| SS_1 | HOCH2CH2S−SCH3 | 388.6 | 3.9 | 4.2 | 1.0 | 1.4 | 1.0 | 1.3 |
| SC_1 | HOCH2CH2S−CH2CH2OH | 392.7 | −0.8 | −0.4 | −2.4 | −2.2 | −1.9 | −1.7 |
| CSi_1 | HOCH2CH2−SiH2F | 394.5 | 7.7 | 6.4 | 1.6 | 0.2 | 2.4 | 1.1 |
| ON_1 | HOCH2CH2O−N(CH3)2 | 398.6 | 6.3 | 8.3 | −4.0 | −2.3 | −3.6 | −1.9 |
| MUE | 7.2 | 7.5 | 2.3 | 2.2 | 2.5 | 2.5 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.-P.; Gagliardi, L.; Truhlar, D.G. Parametrization of Combined Quantum Mechanical and Molecular Mechanical Methods: Bond-Tuned Link Atoms. Molecules 2018, 23, 1309. https://doi.org/10.3390/molecules23061309
Wu X-P, Gagliardi L, Truhlar DG. Parametrization of Combined Quantum Mechanical and Molecular Mechanical Methods: Bond-Tuned Link Atoms. Molecules. 2018; 23(6):1309. https://doi.org/10.3390/molecules23061309
Chicago/Turabian StyleWu, Xin-Ping, Laura Gagliardi, and Donald G. Truhlar. 2018. "Parametrization of Combined Quantum Mechanical and Molecular Mechanical Methods: Bond-Tuned Link Atoms" Molecules 23, no. 6: 1309. https://doi.org/10.3390/molecules23061309
APA StyleWu, X. -P., Gagliardi, L., & Truhlar, D. G. (2018). Parametrization of Combined Quantum Mechanical and Molecular Mechanical Methods: Bond-Tuned Link Atoms. Molecules, 23(6), 1309. https://doi.org/10.3390/molecules23061309