Investigation of Direct Model Transferability Using Miniature Near-Infrared Spectrometers
Abstract
:1. Introduction
2. Results
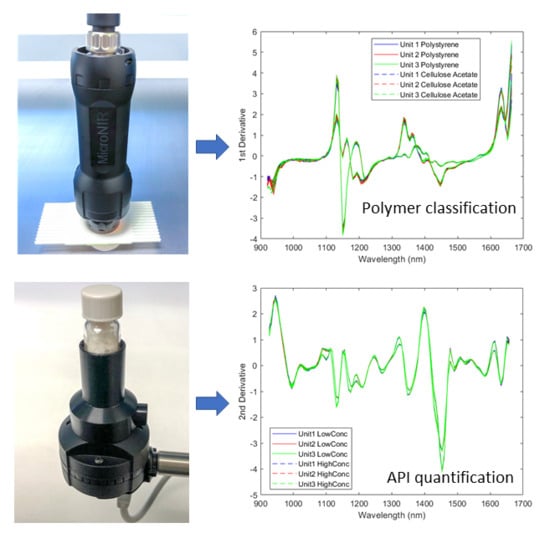
2.1. Classification of Polymers
2.1.1. Spectra of the Resin Samples
2.1.2. Direct Model Transferability of the Classification Models
2.2. Quantification of Active Pharmaceutical Ingredients
2.2.1. Spectra of the Pharmaceutical Samples
2.2.2. Direct Model Transferability of the Quantitative Models
2.2.3. Calibration Transfer
3. Discussion
4. Materials and Methods
4.1. Materials
4.2. Spectra Collection
4.2.1. Resin Samples
4.2.2. Pharmaceutical Samples
4.3. Data Processing and Multivariate Analysis
4.3.1. Polymer Classification
4.3.2. API Quantification
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yan, H.; Siesler, H.W. Hand-held near-infrared spectrometers: State-of-the-art instrumentation and practical applications. NIR News 2018, 29, 8–12. [Google Scholar] [CrossRef]
- Dos Santos, C.A.T.; Lopo, M.; Páscoa, R.N.M.J.; Lopes, J.A. A Review on the Applications of Portable Near-Infrared Spectrometers in the Agro-Food Industry. Appl. Spectrosc. 2013, 67, 1215–1233. [Google Scholar] [CrossRef]
- Santos, P.M.; Pereira-Filho, E.R.; Rodriguez-Saona, L.E. Application of Hand-Held and Portable Infrared Spectrometers in Bovine Milk Analysis. J. Agric. Food Chem. 2013, 61, 1205–1211. [Google Scholar] [CrossRef]
- Alcalà, M.; Blanco, M.; Moyano, D.; Broad, N.; O’Brien, N.; Friedrich, D.; Pfeifer, F.; Siesler, H. Qualitative and quantitative pharmaceutical analysis with a novel handheld miniature near-infrared spectrometer. J. Near Infrared Spectrosc. 2013, 21, 445. [Google Scholar] [CrossRef]
- Paiva, E.M.; Rohwedder, J.J.R.; Pasquini, C.; Pimentel, M.F.; Pereira, C.F. Quantification of biodiesel and adulteration with vegetable oils in diesel/biodiesel blends using portable near-infrared spectrometer. Fuel 2015, 160, 57–63. [Google Scholar] [CrossRef]
- Risoluti, R.; Gregori, A.; Schiavone, S.; Materazzi, S. “Click and Screen” Technology for the Detection of Explosives on Human Hands by a Portable MicroNIR–Chemometrics Platform. Anal. Chem. 2018, 90, 4288–4292. [Google Scholar] [CrossRef]
- Pederson, C.G.; Friedrich, D.M.; Hsiung, C.; von Gunten, M.; O’Brien, N.A.; Ramaker, H.-J.; van Sprang, E.; Dreischor, M. Pocket-size near-infrared spectrometer for narcotic materials identification. In Proceedings Volume 9101, Proceedings of the Next-Generation Spectroscopic Technologies VII, SPIE Sensing Technology + Applications, Baltimore, MD, USA, 10 June 2014; Druy, M.A., Crocombe, R.A., Eds.; International Society for Optics and Photonics: Bellingham, WA, USA, 2014; pp. 91010O-1–91010O-11. [Google Scholar] [CrossRef]
- Wu, S.; Panikar, S.S.; Singh, R.; Zhang, J.; Glasser, B.; Ramachandran, R. A systematic framework to monitor mulling processes using Near Infrared spectroscopy. Adv. Powder Technol. 2016, 27, 1115–1127. [Google Scholar] [CrossRef]
- Galaverna, R.; Ribessi, R.L.; Rohwedder, J.J.R.; Pastre, J.C. Coupling Continuous Flow Microreactors to MicroNIR Spectroscopy: Ultracompact Device for Facile In-Line Reaction Monitoring. Org. Process Res. Dev. 2018, 22, 780–788. [Google Scholar] [CrossRef]
- Feudale, R.N.; Woody, N.A.; Tan, H.; Myles, A.J.; Brown, S.D.; Ferré, J. Transfer of multivariate calibration models: A review. Chemom. Intell. Lab. Syst. 2002, 64, 181–192. [Google Scholar] [CrossRef]
- Workman, J.J. A Review of Calibration Transfer Practices and Instrument Differences in Spectroscopy. Appl. Spectrosc. 2018, 72, 340–365. [Google Scholar] [CrossRef]
- Wang, Y.; Veltkamp, D.J.; Kowalski, B.R. Multivariate instrument standardization. Anal. Chem. 1991, 63, 2750–2756. [Google Scholar] [CrossRef]
- Wang, Y.; Lysaght, M.J.; Kowalski, B.R. Improvement of multivariate calibration through instrument standardization. Anal. Chem. 1992, 64, 562–564. [Google Scholar] [CrossRef]
- Wang, Z.; Dean, T.; Kowalski, B.R. Additive Background Correction in Multivariate Instrument Standardization. Anal. Chem. 1995, 67, 2379–2385. [Google Scholar] [CrossRef]
- Du, W.; Chen, Z.-P.; Zhong, L.-J.; Wang, S.-X.; Yu, R.-Q.; Nordon, A.; Littlejohn, D.; Holden, M. Maintaining the predictive abilities of multivariate calibration models by spectral space transformation. Anal. Chim. Acta 2011, 690, 64–70. [Google Scholar] [CrossRef]
- Martens, H.; Høy, M.; Wise, B.M.; Bro, R.; Brockhoff, P.B. Pre-whitening of data by covariance-weighted pre-processing. J. Chemom. 2003, 17, 153–165. [Google Scholar] [CrossRef]
- Cogdill, R.P.; Anderson, C.A.; Drennen, J.K. Process analytical technology case study, part III: Calibration monitoring and transfer. AAPS Pharm. Sci. Tech. 2005, 6, E284–E297. [Google Scholar] [CrossRef] [Green Version]
- Shi, G.; Han, L.; Yang, Z.; Chen, L.; Liu, X. Near Infrared Spectroscopy Calibration Transfer for Quantitative Analysis of Fish Meal Mixed with Soybean Meal. J. Near Infrared Spectrosc. 2010, 18, 217–223. [Google Scholar] [CrossRef]
- Salguero-Chaparro, L.; Palagos, B.; Peña-Rodríguez, F.; Roger, J.M. Calibration transfer of intact olive NIR spectra between a pre-dispersive instrument and a portable spectrometer. Comput. Electron. Agric. 2013, 96, 202–208. [Google Scholar] [CrossRef] [Green Version]
- Krapf, L.C.; Nast, D.; Gronauer, A.; Schmidhalter, U.; Heuwinkel, H. Transfer of a near infrared spectroscopy laboratory application to an online process analyser for in situ monitoring of anaerobic digestion. Bioresour. Technol. 2013, 129, 39–50. [Google Scholar] [CrossRef]
- Myles, A.J.; Zimmerman, T.A.; Brown, S.D. Transfer of Multivariate Classification Models between Laboratory and Process Near-Infrared Spectrometers for the Discrimination of Green Arabica and Robusta Coffee Beans. Appl. Spectrosc. 2006, 60, 1198–1203. [Google Scholar] [CrossRef]
- Milanez, K.D.T.M.; Silva, A.C.; Paz, J.E.M.; Medeiros, E.P.; Pontes, M.J.C. Standardization of NIR data to identify adulteration in ethanol fuel. Microchem. J. 2016, 124, 121–126. [Google Scholar] [CrossRef]
- Ni, W.; Brown, S.D.; Man, R. Stacked PLS for calibration transfer without standards. J. Chemom. 2011, 25, 130–137. [Google Scholar] [CrossRef]
- Lin, Z.; Xu, B.; Li, Y.; Shi, X.; Qiao, Y. Application of orthogonal space regression to calibration transfer without standards. J. Chemom. 2013, 27, 406–413. [Google Scholar] [CrossRef]
- Kramer, K.E.; Morris, R.E.; Rose-Pehrsson, S.L. Comparison of two multiplicative signal correction strategies for calibration transfer without standards. Chemom. Intell. Lab. Syst. 2008, 92, 33–43. [Google Scholar] [CrossRef]
- Sun, L.; Hsiung, C.; Pederson, C.G.; Zou, P.; Smith, V.; von Gunten, M.; O’Brien, N.A. Pharmaceutical Raw Material Identification Using Miniature Near-Infrared (MicroNIR) Spectroscopy and Supervised Pattern Recognition Using Support Vector Machine. Appl. Spectrosc. 2016, 70, 816–825. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ståhle, L.; Wold, S. Partial least squares analysis with cross-validation for the two-class problem: A Monte Carlo study. J. Chemom. 1987, 1, 185–196. [Google Scholar] [CrossRef]
- Wold, S. Pattern recognition by means of disjoint principal components models. Pattern Recognit. 1976, 8, 127–139. [Google Scholar] [CrossRef]
- Breiman, L. Random Forrest. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A training algorithm for optimal margin classifiers. In Proceedings of the Fifth Annual Workshop on Computational Learning Theory-COLT′92, Pittsburgh, PA, USA, 27 July 1992; pp. 144–152. [Google Scholar]
- Blanco, M.; Bautista, M.; Alcalà, M. API Determination by NIR Spectroscopy Across Pharmaceutical Production Process. AAPS Pharm. Sci. Tech. 2008, 9, 1130–1135. [Google Scholar] [CrossRef] [Green Version]
- Swarbrick, B. The current state of near infrared spectroscopy application in the pharmaceutical industry. J. Near Infrared Spectrosc. 2014, 22, 153–156. [Google Scholar] [CrossRef]
- Gouveia, F.F.; Rahbek, J.P.; Mortensen, A.R.; Pedersen, M.T.; Felizardo, P.M.; Bro, R.; Mealy, M.J. Using PAT to accelerate the transition to continuous API manufacturing. Anal. Bioanal. Chem. 2017, 409, 821–832. [Google Scholar] [CrossRef]
- Kennard, R.W.; Stone, L.A. Computer Aided Design of Experiments. Technometrics 1969, 11, 137–148. [Google Scholar] [CrossRef]
- Sorak, D.; Herberholz, L.; Iwascek, S.; Altinpinar, S.; Pfeifer, F.; Siesler, H.W. New Developments and Applications of Handheld Raman, Mid-Infrared, and Near-Infrared Spectrometers. Appl. Spectrosc. Rev. 2011, 47, 83–115. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D.G. Measuring agreement in method comparison studies. Stat. Methods Med. Res. 1999, 8, 135–160. [Google Scholar] [CrossRef]
- Bennett, K.P.; Campbell, C. Support Vector Machines: Hype or Hallelujah? Sigkdd Explor. Newslett. 2000, 2, 1–13. [Google Scholar] [CrossRef]
- Briand, B.; Ducharme, G.R.; Parache, V.; Mercat-Rommens, C. A similarity measure to assess the stability of classification trees. Comput. Stat. Data Anal. 2009, 53, 1208–1217. [Google Scholar] [CrossRef]
- Wise, B.M.; Roginski, R.T. A Calibration Model Maintenance Roadmap. IFAC-PapersOnLine 2015, 48, 260–265. [Google Scholar] [CrossRef]
- Petersen, L.; Esbensen, K.H. Representative process sampling for reliable data analysis—A tutorial. J. Chemom. 2005, 19, 625–647. [Google Scholar] [CrossRef]
- Romañach, R.; Esbensen, K. Sampling in pharmaceutical manufacturing—Many opportunities to improve today’s practice through the Theory of Sampling (TOS). TOS Forum 2015, 4, 5–9. [Google Scholar] [CrossRef]
- The Effects of Sample Presentation in Near-Infrared (NIR) Spectroscopy. Available online: https://www.viavisolutions.com/en-us/literature/effects-sample-presentation-near-infrared-nir-spectroscopy-application-notes-en.pdf (accessed on 12 March 2019).
- MicroNIRTM Sampling Distance. Available online: https://www.viavisolutions.com/en-us/literature/micronir-sampling-distance-application-notes-en.pdf (accessed on 12 March 2019).
Sample Availability: Not available. |








| Algorithm | Unit# Kit# for Modeling | Unit# Kit# for Testing | |||||
|---|---|---|---|---|---|---|---|
| Unit1 K1 | Unit2 K1 | Unit3 K1 | Unit1 K2 | Unit2 K2 | Unit3 K3 | ||
| PLS-DA | Unit 1 K1 | 99.64 | 89.68 | 83.99 | 95.87 | 88.91 | 82.39 |
| Unit 2 K1 | 91.96 | 100 | 81.52 | 90.87 | 99.57 | 84.49 | |
| Unit 3 K1 | 76.74 | 75.32 | 100 | 75.07 | 73.12 | 99.20 | |
| SIMCA | Unit 1 K1 | 100 | 99.42 | 96.45 | 99.35 | 97.32 | 96.81 |
| Unit 2 K1 | 98.77 | 100 | 95.43 | 97.68 | 99.93 | 95.80 | |
| Unit 3 K1 | 96.30 | 93.29 | 100 | 96.09 | 92.17 | 100 | |
| TreeBagger | Unit 1 K1 | 100 | 97.11 | 95.80 | 98.04 | 95.94 | 96.30 |
| Unit 2 K1 | 97.83 | 100 | 93.55 | 94.49 | 98.26 | 96.16 | |
| Unit 3 K1 | 95.14 | 98.41 | 100 | 96.09 | 98.84 | 98.84 | |
| SVM | Unit 1 K1 | 100 | 99.86 | 97.54 | 98.26 | 97.90 | 97.83 |
| Unit 2 K1 | 98.70 | 100 | 97.03 | 94.93 | 98.26 | 98.26 | |
| Unit 3 K1 | 97.83 | 96.18 | 100 | 96.30 | 95.00 | 99.57 | |
| Hier-SVM | Unit 1 K1 | 100 | 100 | 97.97 | 97.83 | 97.83 | 97.25 |
| Unit 2 K1 | 99.93 | 100 | 98.26 | 98.26 | 99.13 | 99.13 | |
| Unit 3 K1 | 99.13 | 100 | 100 | 96.88 | 97.83 | 100 | |
| Algorithm | Unit# Kit# for Modeling | Unit# Kit# for Testing | |||||
|---|---|---|---|---|---|---|---|
| Unit1 K1 | Unit2 K1 | Unit3 K1 | Unit1 K2 | Unit2 K2 | Unit3 K3 | ||
| PLS-DA | Unit 1 K1 | 1/276 | 143/1386 | 221/1380 | 57/1380 | 153/1380 | 243/1380 |
| Unit 2 K1 | 111/1380 | 0/277 | 255/1380 | 126/1380 | 6/1380 | 214/1380 | |
| Unit 3 K1 | 321/1380 | 342/1386 | 0/276 | 344/1380 | 371/1380 | 11/1380 | |
| SIMCA | Unit 1 K1 | 0/276 | 8/1386 | 49/1380 | 9/1380 | 37/1380 | 44/1380 |
| Unit 2 K1 | 17/1380 | 0/277 | 63/1380 | 32/1380 | 1/1380 | 58/1380 | |
| Unit 3 K1 | 51/1380 | 93/1386 | 0/276 | 54/1380 | 108/1380 | 0/1380 | |
| TreeBagger | Unit 1 K1 | 0/276 | 40/1386 | 58/1380 | 27/1380 | 56/1380 | 51/1380 |
| Unit 2 K1 | 30/1380 | 0/277 | 89/1380 | 76/1380 | 24/1380 | 53/1380 | |
| Unit 3 K1 | 67/1380 | 22/1386 | 0/276 | 54/1380 | 16/1380 | 16/1380 | |
| SVM | Unit 1 K1 | 0/276 | 2/1386 | 34/1380 | 24/1380 | 29/1380 | 30/1380 |
| Unit 2 K1 | 18/1380 | 0/277 | 41/1380 | 70/1380 | 24/1380 | 24/1380 | |
| Unit 3 K1 | 30/1380 | 53/1386 | 0/276 | 51/1380 | 69/1380 | 6/1380 | |
| Hier-SVM | Unit 1 K1 | 0/276 | 0/1386 | 28/1380 | 30/1380 | 30/1380 | 38/1380 |
| Unit 2 K1 | 1/1380 | 0/277 | 24/1380 | 24/1380 | 12/1380 | 12/1380 | |
| Unit 3 K1 | 12/1380 | 0/1386 | 0/276 | 43/1380 | 30/1380 | 0/1380 | |
| Test Sets | No Correction | Bias | PDS | GLS | ||
|---|---|---|---|---|---|---|
| Unit 1 | Unit 2 | Unit 3 | Unit 1 | Unit 1 | Unit 1 | |
| Unit 1 | 3.4 | 3.5 | 3.5 | - | - | - |
| Unit 2 | 4.0 | 4.2 | 3.9 | 3.7 | 3.3 | 3.6 |
| Unit 3 | 4.3 | 4.5 | 4.2 | 4.1 | 3.5 | 4.4 |
| Test Sets | No Correction | Bias | PDS | GLS | ||
|---|---|---|---|---|---|---|
| Unit 1 | Unit 2 | Unit 3 | Unit 1 | Unit 1 | Unit 1 | |
| Unit 1 | 3.0 | 2.6 | 2.7 | - | - | - |
| Unit 2 | 2.7 | 2.7 | 2.6 | 2.3 | 3.5 | 2.6 |
| Unit 3 | 2.5 | 2.5 | 2.7 | 2.2 | 3.1 | 2.4 |
| Test Sets | No Correction | Bias | PDS | GLS | ||
|---|---|---|---|---|---|---|
| Unit 1 | Unit 2 | Unit 3 | Unit 1 | Unit 1 | Unit 1 | |
| Unit 1 | 4.0 | 4.6 | 3.7 | - | - | - |
| Unit 2 | 4.1 | 4.7 | 4.2 | 4.2 | 4.3 | 3.2 |
| Unit 3 | 4.2 | 4.9 | 4.0 | 4.1 | 6.2 | 3.9 |
| No. | Polymer Type | No. | Polymer Type |
|---|---|---|---|
| 1 | PolyStyrene-General Purpose | 24 | Polyethylene-High Density |
| 2 | PolyStyrene-High Impact | 25 | Polypropylene-Copolymer |
| 3 | Styrene-Acrylonitrile (SAN) | 26 | Polypropylene-Homopolymer |
| 4 | ABS-Transparent | 27 | Polyaryl-Ether |
| 5 | ABS-Medium Impact | 28 | Polyvinyl Chloride-Flexible |
| 6 | ABS-High Impact | 29 | Polyvinyl Chloride-Rigid |
| 7 | Styrene Butadiene | 30 | Acetal Resin-Homopolymer |
| 8 | Acrylic | 31 | Acetal Resin-Copolymer |
| 9 | Modified Acrylic | 32 | Polyphenylene Sulfide |
| 10 | Cellulose Acetate | 33 | Ethylene Vinyl Acetate |
| 11 | Cellulose Acetate Butyrate | 34 | Urethane Elastomer (Polyether) |
| 12 | Cellulose Acetate Propionate | 35 | Polypropylene-Flame Retardant |
| 13 | Nylon-Transparent | 36 | Polyester Elastomer |
| 14 | Nylon-Type 66 | 37 | ABS-Flame Retardant |
| 15 | Nylon-Type 6 (Homopolymer) | 38 | Polyallomer |
| 16 | Thermoplastic Polyester (PBT) | 39 | Styrenic Terpolymer |
| 17 | Thermoplastic Polyester (PETG) | 40 | Polymethyl Pentene |
| 18 | Phenylene Oxide | 41 | Talc-Reinforced Polypropylene |
| 19 | Polycarbonate | 42 | Calcium Carbonate-Reinforced Polypropylene |
| 20 | Polysulfone | 43 | Nylon (Type 66–33% Glass) |
| 21 | Polybutylene | 44 | Thermoplastic Rubber |
| 22 | Ionomer | 45 | Polyethylene (Medium Density) |
| 23 | Polyethylene-Low Density | 46 | ABS-Nylon Alloy |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, L.; Hsiung, C.; Smith, V. Investigation of Direct Model Transferability Using Miniature Near-Infrared Spectrometers. Molecules 2019, 24, 1997. https://doi.org/10.3390/molecules24101997
Sun L, Hsiung C, Smith V. Investigation of Direct Model Transferability Using Miniature Near-Infrared Spectrometers. Molecules. 2019; 24(10):1997. https://doi.org/10.3390/molecules24101997
Chicago/Turabian StyleSun, Lan, Chang Hsiung, and Valton Smith. 2019. "Investigation of Direct Model Transferability Using Miniature Near-Infrared Spectrometers" Molecules 24, no. 10: 1997. https://doi.org/10.3390/molecules24101997
APA StyleSun, L., Hsiung, C., & Smith, V. (2019). Investigation of Direct Model Transferability Using Miniature Near-Infrared Spectrometers. Molecules, 24(10), 1997. https://doi.org/10.3390/molecules24101997