Enhanced Near-Field Chirality in Periodic Arrays of Si Nanowires for Chiral Sensing
Abstract
:1. Introduction
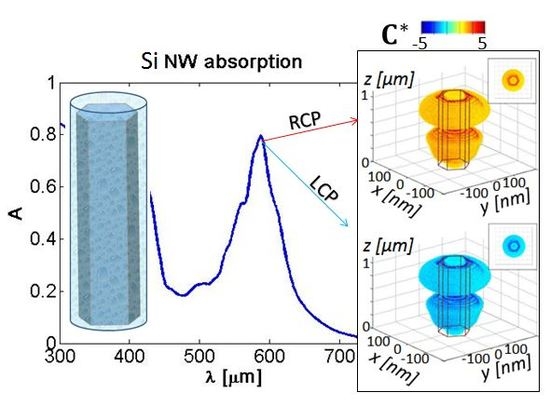
2. Results
2.1. Influence of the NW Core Radius
2.2. Influence of the NW Array Periodicity
2.3. Influence of the NW Length
3. Discussion
4. Materials and Methods
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kelvin, L. The Molecular Tactics of a Crystal; Clarendon Press: Oxford, UK, 1894. [Google Scholar]
- Nguyen, L.A.; He, H.; Pham-Huy, C. Chiral Drugs: An Overview. Int. J. Biomed. Sci. 2006, 2, 85–100. [Google Scholar] [PubMed]
- Hutt, A.J.; Tan, S.C. Drug chirality and its clinical significance. Drugs 1996, 52, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Smith, S.W. Chiral Toxicology: It’s the same thing… Only different. Toxicol. Sci. 2009, 110, 4–30. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.N.; Chen, P.-A.; Setthakarn, K.; May, J.A. Chiral Diol-Based Organocatalysts in Enantioselective Reactions. Molecules 2018, 23, 2317. [Google Scholar] [CrossRef] [PubMed]
- Teo, S.K.; Colburn, W.A.; Tracewell, W.; Kook, K.; Stirling, D.; Jaworsky, M.; Scheffler, M.; Thomas, S.; Laskin, O. Clinical pharmacokinetics of thalidomide. Clin. Pharmacokinet. 2004, 45, 311–327. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, C.; Santos, C.; Gonçalves, V.; Ramos, A.; Afonso, C.; Tiritan, M.E. Chiral Drug Analysis in Foresnic Chemistry: An Overview. Molecules 2018, 23, 262. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Li, M.; Liu, Y.; Wang, F.; Kong, Z.; Sun, Y.; Lu, J.; Jin, N.; Huang, Y.; Liu, J.; et al. Residue and Dietary Risk Assessment of Chiral Cyflumetofen in Apple. Molecules 2018, 23, 1060. [Google Scholar] [CrossRef] [PubMed]
- Rodger, A.; Nordén, B. Circular Dichroism and Linear Dichroism; Oxford Univ. Press: Oxford, UK, 1997. [Google Scholar]
- Valev, V.K.; Baumberg, J.J.; Sibilia, C.; Verbiest, T. Chirality and chiroptical effects in plasmonic nanostructures: Fundamentals, recent progress, and outlook. Adv. Mater. 2013, 25, 2517–2534. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Cheng, F.; Winsor, T.; Liu, Y. Optical chiral metamaterials: A review of the fundamentals, fabrication methods and applications. Nanotechnology 2016, 27, 412001. [Google Scholar] [CrossRef] [PubMed]
- Belardini, A.; Larciprete, M.C.; Centini, M.; Fazio, E.; Sibilia, C.; Chiappe, D.; Martella, C.; Toma, A.; Giordano, M.; Buatier de Mongeot, F. Circular dichroism in the optical second-harmonic emission of curved gold metal nanowires. Phys. Rev. Lett. 2011, 107, 257401. [Google Scholar] [CrossRef] [PubMed]
- Belardini, A.; Centini, M.; Leahu, G.; Fazio, E.; Sibilia, C.; Haus, J.W.; Sarangan, A. Second harmonic generation on self-assembled tilted gold nanowires. Faraday Discuss. 2015, 178, 357–362. [Google Scholar] [CrossRef] [PubMed]
- Belardini, A.; Centini, M.; Leahu, G.; Hooper, D.C.; Li Voti, R.; Fazio, E.; Haus, J.W.; Sarangan, A.; Valev, V.K.; Sibilia, C. Chiral light intrinsically couples to extrinsic/pseudo-chiral metasurfaces made of tilted gold nanowires. Sci. Rep. 2016, 6, 31796. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bertolotti, M.; Belardini, A.; Benedetti, A.; Sibilia, C. Second harmonic circular dichroism by self-assembled metasurfaces. J. Opt. Soc. Am. B 2015, 32, 1287–1293. [Google Scholar] [CrossRef]
- Ma, X.; Pu, M.; Li, X.; Guo, Y.; Gao, P.; Luo, X. Meta-Chirality: Fundamentals, Construction and Applications. Nanomaterials 2017, 7, 116. [Google Scholar] [Green Version]
- Leahu, G.; Petronijevic, E.; Belardini, A.; Centini, M.; Sibilia, C.; Hakkarainen, T.; Koivusalo, E.; Rizzo Piton, M.; Suomalainen, S.; Guina, M. Evidence of optical circular dichroism in GaAs-based nanowires partially covered with gold. Adv. Opt. Mater. 2017, 5, 1601063. [Google Scholar] [CrossRef]
- Petronijevic, E.; Leahu, G.; Belardini, A.; Centini, M.; Li Voti, R.; Hakkarainen, T.; Koivusalo, E.; Rizzo Piton, M.; Suomalainen, S.; Guina, M.; et al. Photo-Acoustic Spectroscopy Reveals Extrinsic Optical Chirality in GaAs-Based Nanowires Partially Covered with Gold. Int. J. Thermophys. 2018, 39, 46. [Google Scholar] [CrossRef]
- Petronijevic, E.; Leahu, G.; Li Voti, R.; Belardini, A.; Scian, C.; Michieli, N.; Cesca, T.; Mattei, G.; Sibilia, C. Photo-acoustic detection of chirality in metal-polystyrene metasurfaces. Appl. Phys. Lett. 2019, 114, 053101. [Google Scholar] [CrossRef]
- Kong, X.-T.; Besteiro, L.V.; Wang, Z.; Govorov, A.O. Plasmonic Chirality and Circular Dichroism in Bioassembled and Nonbiological Systems: Theoretical Background and Recent Progress. Adv. Mater. 2018, 1801790. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Askarpour, A.N.; Sun, L.; Shi, J.; Li, X.; Alù, A. Chirality detection of enantiomers using twisted optical metamaterials. Nat. Commun. 2017, 8, 14180. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hendry, E.; Carpy, T.; Johnston, J.; Popland, M.; Mikhaylovskiy, R.V.; Lapthorn, A.J.; Kelly, S.M.; Barron, L.D.; Gadegaard, N.; Kadodwala, M. Ultrasensitive detection and characterization of biomolecules using superchiral fields. Nat. Nanotechnol. 2010, 5, 783–787. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tang, Y.; Cohen, A.E. Enhanced enantioselectivity in excitation of chiral molecules by superchiral light. Science 2011, 332, 333–336. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Cohen, A.E. Optical chirality and its interaction with matter. Phys. Rev. Lett. 2010, 104, 163901. [Google Scholar] [CrossRef] [PubMed]
- Vázquez-Guardado, A.; Chanda, D. Superchiral Light Generation on Degenerate Achiral Surfaces. Phys. Rev. Lett. 2018, 120, 137601. [Google Scholar] [CrossRef] [PubMed]
- Petronijevic, E.; Centini, M.; Belardini, A.; Leahu, G.; Hakkarainen, T.; Sibilia, C. Chiral near-field manipulation in Au-GaAs hybrid hexagonal nanowires. Opt. Express 2017, 25, 17841–17848. [Google Scholar] [CrossRef] [PubMed]
- Schäferling, M.; Yin, X.; Giessen, H. Formation of chiral fields in a symmetric environment. Opt. Express 2012, 20, 26326–26336. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Davis, T.J.; Hendry, E. Superchiral electromagnetic fields created by surface plasmons in nonchiral metallic nanostructures. Phys. Rev. B 2013, 87, 085405. [Google Scholar] [CrossRef]
- Fountaine, K.T.; Whitney, W.S.; Atwater, H.A. Resonant absorption in semiconductor nanowires and nanowire arrays: Relating leaky waveguide modes to Bloch photonic crystal modes. J. Appl. Phys. 2014, 116, 153106. [Google Scholar] [CrossRef] [Green Version]
- Leahu, G.; Petronijevic, E.; Belardini, A.; Centini, M.; Li Voti, R.; Hakkarainen, T.; Koivusalo, E.; Guina, M.; Sibilia, C. Photo-acoustic spectroscopy revealing resonant absorption of self-assembled GaAs-based nanowires. Sci. Rep. 2017, 7, 2833. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Petronijevic, E.; Leahu, G.; Belardini, A.; Centini, M.; Li Voti, R.; Hakkarainen, T.; Koivusalo, E.; Guina, M.; Sibilia, C. Resonant Absorption in GaAs-Based Nanowires by Means of Photo-Acoustic Spectroscopy. Int. J. Thermophys. 2018, 39, 45. [Google Scholar] [CrossRef]
- Zhao, X.; Alizadeh, M.H.; Reinhard, B.M. Generating Optical Birefringence and Chirality in Silicon Nanowire Dimers. ACS Photonics 2017, 4, 2265–2273. [Google Scholar] [CrossRef]
- Seo, K.; Wober, M.; Steinvurzel, P.; Schonbrun, E.; Dan, Y.; Ellenbogen, T.; Crozier, K.B. Multicolored Vertical Silicon Nanowires. Nano Lett. 2011, 11, 1851–1856. [Google Scholar] [CrossRef] [PubMed]
- Lumerical Solutions, Inc. Available online: http://www.lumerical.com/tcad-products/fdtd/ (accessed on 20 February 2019).
- Azizur-Rahman, K.M.; LaPierre, R.R. Wavelength-selective absorptance in GaAs, InP and InAs nanowire arrays. Nanotechnology 2015, 26, 295202. [Google Scholar] [CrossRef] [PubMed]
- Cao, A.; Sudhölter, E.J.R.; de Smet, L.C.P.M. Silicon Nanowire-Based Devices for Gas-Phase Sensing. Sensors 2014, 14, 245–271. [Google Scholar] [CrossRef] [PubMed]
- Su, S.; Wei, X.; Zhong, Y.; Guo, Y.; Su, Y.; Huang, Q.; Lee, S.-T.; Fan, C.; He, Y. Silicon nanowire-based molecular beacons for high-sensitivity and sequence-specific DNA multiplexed analysis. ACS Nano 2012, 6, 2582–2590. [Google Scholar] [CrossRef] [PubMed]
- Ruizendaal, L.; Pujari, S.P.; Gevaerts, V.; Paulusse, J.M.J.; Zuilhof, H. Biofunctional Silicon Nanoparticles by Means of Thiol-Ene Click Chemistry. Chem. Asian J. 2011, 6, 2776–2786. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Sample Availability: Samples of the compounds are not available from the authors. |






© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petronijevic, E.; Sibilia, C. Enhanced Near-Field Chirality in Periodic Arrays of Si Nanowires for Chiral Sensing. Molecules 2019, 24, 853. https://doi.org/10.3390/molecules24050853
Petronijevic E, Sibilia C. Enhanced Near-Field Chirality in Periodic Arrays of Si Nanowires for Chiral Sensing. Molecules. 2019; 24(5):853. https://doi.org/10.3390/molecules24050853
Chicago/Turabian StylePetronijevic, Emilija, and Concita Sibilia. 2019. "Enhanced Near-Field Chirality in Periodic Arrays of Si Nanowires for Chiral Sensing" Molecules 24, no. 5: 853. https://doi.org/10.3390/molecules24050853
APA StylePetronijevic, E., & Sibilia, C. (2019). Enhanced Near-Field Chirality in Periodic Arrays of Si Nanowires for Chiral Sensing. Molecules, 24(5), 853. https://doi.org/10.3390/molecules24050853