Nanoindentation of Graphene-Reinforced Silica Aerogel: A Molecular Dynamics Study
Abstract
:1. Introduction
2. Methods and Materials
2.1. Creation of the All-Atom Silica Aerogel Model
2.2. Simulation Details
3. Results and Discussion
3.1. Indentation of Graphene
3.2. Indentation of Silica Aerogel
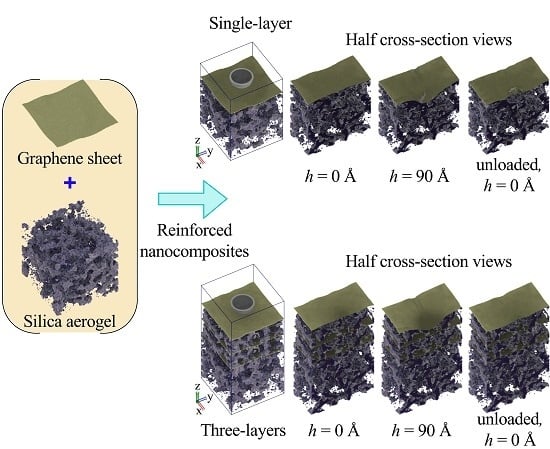
3.3. Single-Layer Graphene-Reinforced Silica Aerogel
3.4. Graphene-Reinforced Multilayered Silica Aerogel Nanocomposites
4. Conclusions
Supplementary Materials
Funding
Acknowledgments
Conflicts of Interest
References
- Hüsing, N.; Schubert, U. Aerogele–luftige materialien: Chemie, struktur und eigenschaften. Angew. Chem. 1998, 110, 22–47. [Google Scholar] [CrossRef]
- Hrubesh, L.W. Aerogel applications. J. Non-Cryst. Solids 1998, 225, 335–342. [Google Scholar] [CrossRef]
- Parale, V.G.; Lee, K.Y.; Park, H.H. Flexible and transparent silica aerogels: An overview. J. Korean Ceram. Soc. 2017, 54, 184–199. [Google Scholar] [CrossRef]
- Koebel, M.; Rigacci, A.; Achard, P. Aerogels Handbook; Springer: New York, NY, USA, 2011; pp. 607–633. [Google Scholar]
- Smirnova, I.; Gurikov, P. Aerogels in chemical engineering: Strategies toward tailor-made aerogels. Annu. Rev. Chem. Biomol. Eng. 2017, 8, 307–334. [Google Scholar] [CrossRef]
- In, E.; Naguib, H.E. Development of Mechanically Stable Polymer-Based Silica Aerogel. Cell. Polym. 2011, 30, 1–12. [Google Scholar] [CrossRef]
- Randall, J.P.; Meador, M.A.B.; Jana, S.C. Polymer reinforced silica aerogels: Effects of dimethyldiethoxysilane and bis (trimethoxysilylpropyl) amine as silane precursors. J. Mater. Chem. A 2013, 1, 6642–6652. [Google Scholar] [CrossRef]
- Wei, T.Y.; Lu, S.Y.; Chang, Y.C. A new class of opacified monolithic aerogels of ultralow high-temperature thermal conductivities. J. Phys. Chem. C 2009, 113, 7424–7428. [Google Scholar] [CrossRef]
- Ślosarczyk, A. Synthesis and characterization of silica aerogel-based nanocomposites with carbon fibers and carbon nanotubes in hybrid system. J. Sol-Gel Sci. Technol. 2017, 84, 16–22. [Google Scholar] [CrossRef]
- Wang, B.; Song, K.; Han, Y.; Zhang, T. Synthesis and characterization of multi-walled carbon nanotube doped silica aerogels. J. Wuhan Univ. Technol.-Mater. Sci. Ed. 2012, 27, 512–515. [Google Scholar] [CrossRef]
- Sun, T.; Zhuo, Q.; Liu, X.; Sun, Z.; Wu, Z.; Fan, H. Hydrophobic silica aerogel reinforced with carbon nanotube for oils removal. J. Porous Mater. 2014, 21, 967–973. [Google Scholar] [CrossRef]
- Loche, D.; Malfatti, L.; Carboni, D.; Alzari, V.; Mariani, A.; Casula, M.F. Incorporation of graphene into silica-based aerogels and application for water remediation. RSC Adv. 2016, 6, 66516–66523. [Google Scholar] [CrossRef] [Green Version]
- Lei, Y.; Hu, Z.; Cao, B.; Chen, X.; Song, H. Enhancements of thermal insulation and mechanical property of silica aerogel monoliths by mixing graphene oxide. Mater. Chem. Phys. 2017, 187, 183–190. [Google Scholar] [CrossRef]
- Dervin, S.; Lang, Y.; Perova, T.; Hinder, S.H.; Pillai, S.C. Graphene oxide reinforced high surface area silica aerogels. J. Non-Cryst. Solids 2017, 465, 31–38. [Google Scholar] [CrossRef] [Green Version]
- Gelb, L.D. Simulating silica aerogels with a coarse-grained flexible model and langevin dynamics. J. Phys. Chem. C 2007, 111, 15792–15802. [Google Scholar] [CrossRef]
- Murillo, J.S.R.; Bachlechner, M.E.; Campo, F.A.; Barbero, E.J. Structure and mechanical properties of silica aerogels and xerogels modeled by molecular dynamics simulation. J. Non-Cryst. Solids 2010, 356, 1325–1331. [Google Scholar] [CrossRef]
- Lei, J.; Liu, Z.; Yeo, J.; Ng, T.Y. Determination of the Young’s modulus of silica aerogels–an analytical–numerical approach. Soft Matter 2013, 9, 11367–11373. [Google Scholar] [CrossRef]
- Ferreiro-Rangel, C.A.; Gelb, L.D. Investigation of the bulk modulus of silica aerogel using molecular dynamics simulations of a coarse-grained model. J. Phys. Chem. B 2013, 117, 7095–7105. [Google Scholar] [CrossRef] [PubMed]
- Ferreiro-Rangel, C.A.; Gelb, L.D. Computational study of uniaxial deformations in silica aerogel using a coarse-grained model. J. Phys. Chem. B 2015, 119, 8640–8650. [Google Scholar] [CrossRef]
- Patil, S.P.; Rege, A.; Itskov, M.; Markert, B. Mechanics of Nanostructured Porous Silica Aerogel Resulting from Molecular Dynamics Simulations. J. Phys. Chem. B 2017, 121, 5660–5668. [Google Scholar] [CrossRef]
- Gonçalves, W.; Morthomas, J.; Chantrenne, P.; Perez, M.; Foray, G.; Martin, C.L. Elasticity and strength of silica aerogels: A molecular dynamics study on large volumes. Acta Mater. 2018, 145, 165–174. [Google Scholar] [CrossRef]
- Patil, S.P.; Rege, A.; Itskov, M.; Markert, B. Fracture of silica aerogels: An all-atom simulation study. J. Non-Cryst. Solids 2018, 498, 125–129. [Google Scholar] [CrossRef]
- Patil, S.P.; Parale, V.G.; Park, H.H.; Markert, B. Molecular dynamics and experimental studies of nanoindentation on nanoporous silica aerogels. Mater. Sci. Eng. A 2019, 742, 344–352. [Google Scholar] [CrossRef]
- Schuh, C.A. Nanoindentation studies of materials. Mater. Today 2006, 9, 32–40. [Google Scholar] [CrossRef]
- Parmenter, K.E.; Milstein, F. Mechanical properties of silica aerogels. J. Non-Cryst. Solids 1998, 223, 179–189. [Google Scholar] [CrossRef]
- Kucheyev, S.; Baumann, T.; Cox, C.; Wang, Y.; Satcher, J., Jr.; Hamza, A.; Bradby, J. Nanoengineering mechanically robust aerogels via control of foam morphology. Appl. Phys. Lett. 2006, 89, 041911. [Google Scholar] [CrossRef]
- Moner-Girona, M.; Martínez, E.; Esteve, J.; Roig, A.; Solanas, R.; Molins, E. Micromechanical properties of carbon–silica aerogel composites. Appl. Phys. A 2002, 74, 119–122. [Google Scholar] [CrossRef]
- Lucas, E.M.; Doescher, M.S.; Ebenstein, D.M.; Wahl, K.J.; Rolison, D.R. Silica aerogels with enhanced durability, 30-nm mean pore-size, and improved immersibility in liquids. J. Non-Cryst. Solids 2004, 350, 244–252. [Google Scholar] [CrossRef]
- De la Rosa-Fox, N.; Morales-Florez, V.; Toledo-Fernandez, J.A.; Pinero, M.; Mendoza-Serna, R.; Esquivias, L. Nanoindentation on hybrid organic/inorganic silica aerogels. J. Eur. Ceram. Soc. 2007, 27, 3311–3316. [Google Scholar] [CrossRef]
- Kucheyev, S.; Hamza, A.; Satcher, J., Jr.; Worsley, M. Depth-sensing indentation of low-density brittle nanoporous solids. Acta Mater. 2009, 57, 3472–3480. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO—The Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
- Vashishta, P.; Kalia, R.K.; Rino, J.P.; Ebbsjö, I. Interaction potential for SiO2: A molecular-dynamics study of structural correlations. Phys. Rev. B 1990, 41, 12197–12209. [Google Scholar] [CrossRef]
- Vashishta, P.; Kalia, R.K.; Nakano, A.; Li, W.; Ebbsjö, I. Molecular dynamics methods and large-scale simulations of amorphous materials. Amorph. Insul. Semicond. 1996, 33, 151–213. [Google Scholar]
- Wyckoff, R.W. Structure of Crystals; The Chemical Catalog Company, Inc.: New York, NY, USA, 1924. [Google Scholar]
- Stuart, S.J.; Tutein, A.B.; Harrison, J.A. A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 2000, 112, 6472–6486. [Google Scholar] [CrossRef]
- Dewapriya, M.; Arachchige, M. Molecular Dynamics Study of Effects of Geometric Defects on the Mechanical Properties of Graphene. Master’s Thesis, The University of British Columbia, Vancouver, BC, Canada, 2012. [Google Scholar]
- Zhang, B.; Mei, L.; Xiao, H. Nanofracture in graphene under complex mechanical stresses. Appl. Phys. Lett. 2012, 101, 121915. [Google Scholar] [CrossRef]
- Cao, A.; Qu, J. Atomistic simulation study of brittle failure in nanocrystalline graphene under uniaxial tension. Appl. Phys. Lett. 2013, 102, 071902. [Google Scholar] [CrossRef]
- Rappé, A.K.; Casewit, C.J.; Colwell, K.; Goddard, W., III; Skiff, W. UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. [Google Scholar] [CrossRef]
- Xiao, J.; Dunham, S.; Liu, P.; Zhang, Y.; Kocabas, C.; Moh, L.; Huang, Y.; Hwang, K.C.; Lu, C.; Huang, W.; et al. Alignment controlled growth of single-walled carbon nanotubes on quartz substrates. Nano Lett. 2009, 9, 4311–4319. [Google Scholar] [CrossRef]
- Ong, Z.Y.; Pop, E. Molecular dynamics simulation of thermal boundary conductance between carbon nanotubes and SiO2. Phys. Rev. B 2010, 81, 155408. [Google Scholar] [CrossRef]
- Haile, J.; Johnston, I.; Mallinckrodt, A.J.; McKay, S. Molecular dynamics simulation: Elementary methods. Comput. Phys. 1993, 7, 625. [Google Scholar] [CrossRef]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef] [PubMed]
- Schneider, T.; Stoll, E. Molecular-dynamics study of a three-dimensional one-component model for distortive phase transitions. Phys. Rev. B 1978, 17, 1302. [Google Scholar] [CrossRef]
Sample Availability: Samples of the compounds are not available from the authors. |






| Simulation System | Model Size | Number of Atoms (millions) | ||
|---|---|---|---|---|
| x × y × z (Å) | Graphene | Silica Aerogel | MD * Model | |
| Graphene | ∼407.0 × 407.0 × 3.4 | 0.127 | - | 0.127 |
| Native silica aerogel | ∼407.0 × 407.0 × 407.0 | - | 0.786 | 0.786 |
| 1G-SiO | ∼407.0 × 407.0 × 410.4 | 0.127 | 0.786 | 0.913 |
| 2G-1SL-I-SiO | ∼407.0 × 407.0 × 467.9 | 0.254 | 0.884 | 1.138 |
| 3G-2SL-I-SiO | ∼407.0 × 407.0 × 524.3 | 0.381 | 0.982 | 1.363 |
| 2G-1SL-II-SiO | ∼407.0 × 407.0 × 543.8 | 0.254 | 1.032 | 1.286 |
| 3G-2SL-II-SiO | ∼407.0 × 407.0 × 676.0 | 0.381 | 1.278 | 1.659 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patil, S.P. Nanoindentation of Graphene-Reinforced Silica Aerogel: A Molecular Dynamics Study. Molecules 2019, 24, 1336. https://doi.org/10.3390/molecules24071336
Patil SP. Nanoindentation of Graphene-Reinforced Silica Aerogel: A Molecular Dynamics Study. Molecules. 2019; 24(7):1336. https://doi.org/10.3390/molecules24071336
Chicago/Turabian StylePatil, Sandeep P. 2019. "Nanoindentation of Graphene-Reinforced Silica Aerogel: A Molecular Dynamics Study" Molecules 24, no. 7: 1336. https://doi.org/10.3390/molecules24071336
APA StylePatil, S. P. (2019). Nanoindentation of Graphene-Reinforced Silica Aerogel: A Molecular Dynamics Study. Molecules, 24(7), 1336. https://doi.org/10.3390/molecules24071336