Cryostructuring of Polymeric Systems †: Application of Deep Neural Networks for the Classification of Structural Features Peculiar to Macroporous Poly(vinyl alcohol) Cryogels Prepared without and with the Additives of Chaotropes or Kosmotropes †
Abstract
:1. Introduction
2. Results and Discussion
2.1. Physico-Mechanical Properties of PVACGs Prepared at Different Freezing Temperatures and in the Absence or the Presence of Chaotropic or Kosmotropic Additives
- (i)
- The ‘intensity’ of the increase or decrease of the ratios G0ac/G0af and G20ac/G20af depended on the chaotropic or kosmotropic properties of the additives, and such an ‘intensity’ was, as a rule, different with respect to the elastic and plastic characteristics of the PVACGs under study.
- (ii)
- This ‘intensity’ was also sensitive to the presence or absence of a charge in the molecules of a particular low-molecular additive.
- (iii)
- The character of the G0ac/G0af and G20ac/G20af variations with an increase in the additive amount was dependent on the cryogenic processing temperature (Tcp) which was used for the PVACGs preparation.
2.2. Heat Endurance of PVACGs Prepared at Different Freezing Temperatures in the Absence or Presence of Chaotropic or Kosmotropic Additives
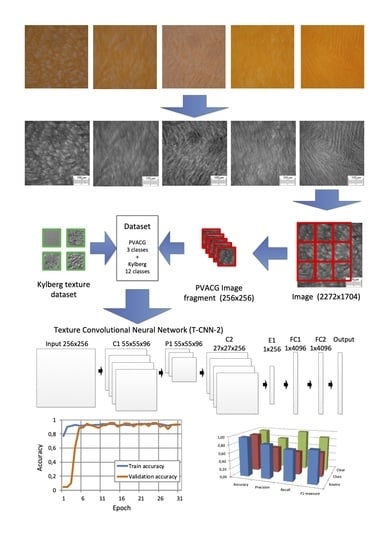
2.3. Morphometric Analysis of the Structural Features of PVACGs Prepared in Absence and Presence of Chaotropic or Kosmotropic Additives
3. Materials and Methods
3.1. Materials
3.2. Preparation of PVA Solutions with and without the Soluble Low-Molecular Additives
3.3. Preparation of Cryogel Samples
3.4. Physicochemical Characteristics of PVACG Samples
3.5. Optical Microscopy of PVACGs
3.6. Morphometric Analysis of the Microscopy Images
3.6.1. Classification
- (i)
- The presence of additives (two classes: there are additives, no additives).
- (ii)
- The type of additives (three classes: kosmotropes, chaotropes, no additives).
- (iii)
- Particular additives (five classes: four substances and without additives).
- (iv)
- Concentration of the additives (two classes).
- (v)
- Cryogenic processing temperature (four classes: −20 to −35 with 5 degree steps)
3.6.2. Creating a Dataset
3.6.3. Neural Network Architecture
3.6.4. Classification Quality Metrics
- Accuracy;
- Precision;
- Recall;
- F1-measure.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Okay, O. (Ed.) Polymeric Cryogels: Macroporous Gels with Remarkable Properties; Springer: Cham, Switzerland, 2014; p. 330. ISSN 0065-3195. [Google Scholar]
- Lozinsky, V.I. Cryostructuring of polymer systems. 50. Cryogels and cryotropic gel-formation: Terms and definitions. Gels 2018, 4, 77. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lozinsky, V.I. Cryogels on the basis of natural and synthetic polymers: Preparation, properties and areas of implementation. Russ. Chem. Rev. 2002, 71, 489–511. [Google Scholar] [CrossRef]
- Gun’ko, V.M.; Savina, I.N.; Mikhalovsky, S.V. Cryogels: Morphological, structural and adsorption characteristics. Adv. Coll. Interface Sci. 2013, 187–188, 1–46. [Google Scholar] [CrossRef] [Green Version]
- Lozinsky, V.I.; Okay, O. Basic principles of cryotropic gelation. Adv. Polym. Sci. 2014, 263, 49–102. [Google Scholar] [CrossRef]
- Reichelt, S. Introduction to macroporous cryogels. Meth. Molec. Biol. 2015, 1286, 173–181. [Google Scholar] [CrossRef]
- Raina, D.B.; Kumar, A. Cryogels and related research: A glance over the past few decades. In Supermacroporous Cryogels: Biomedical and Biotechnological Application; Kumar, A., Ed.; CRC Press: Boca Raton, FL, USA, 2016; pp. 3–34. ISBN 9781482228816. [Google Scholar]
- Zhang, H.; Cooper, A.I. Aligned porous structures by directional freezing. Adv. Mater. 2007, 19, 1529–1533. [Google Scholar] [CrossRef]
- Okay, O.; Lozinsky, V.I. Synthesis, structure-property relationships of cryogels. Adv. Polym. Sci. 2014, 263, 103–157. [Google Scholar] [CrossRef]
- Lozinsky, V.I. Cryostructuring of polymeric systems. 55. Retrospective view on the more than 40-years studies performed in the A.N.Nesmeyanov Institute of Organoelement Compounds with respect of the cryostructuring processes in polymeric systems. Gels 2020, 6, 29. [Google Scholar] [CrossRef]
- Varfolomeyev, S.D.; Rainina, E.I.; Lozinsky, V.I. Cryoimmobilized enzymes and cells in organic synthesis. Pure Appl. Chem. 1992, 64, 1193–1196. [Google Scholar] [CrossRef] [Green Version]
- Lozinsky, V.I.; Plieva, F.M.; Galaev, I.Y.; Mattiasson, B. The potential of polymeric cryogels in bioseparation. Bioseparation 2001, 10, 163–188. [Google Scholar] [CrossRef]
- Lozinsky, V.I.; Galaev, I.Y.; Plieva, F.M.; Savina, I.N.; Jungvid, H.; Mattiasson, B. Polymeric cryogels as promising materials of biotechnological interest. Trends Biotechnol. 2003, 21, 445–451. [Google Scholar] [CrossRef] [PubMed]
- Altunina, L.K.; Kuvshinov, V.A.; Dolgikh, S.N. Cryogels—A promising material for underground works in permafrost. In Advances in Geological Storage of Carbon Dioxide; Lombardi, S., Altunina, L.K., Beaubien, S.E., Eds.; NATO Science Series IV; Springer: Heidelberg, Germany, 2006; pp. 103–110. ISBN 13 978-1-4020-4469-4. [Google Scholar]
- Plieva, F.M.; Galaev, I.Y.; Noppe, W.; Mattiasson, B. Cryogel applications in microbiology. J. Microb. Meth. 2008, 16, 543–551. [Google Scholar] [CrossRef] [PubMed]
- Lozinsky, V.I. New generation of macroporous and supermacroporous materials of biotechnological interest—Polymeric cryogels. Russ. Chem. Bull. 2008, 57, 1015–1032. [Google Scholar] [CrossRef]
- Smith, T.J.; Kennedy, J.E.; Higginbotham, C.L. Rheological and thermal characteristics of a two phase hydrogel system for potential wound healing applications. J. Mater. Sci. 2010, 45, 2884–2891. [Google Scholar] [CrossRef]
- Mattiasson, B. Cryogels for biotechnological applications. Adv. Polym. Sci. 2014, 263, 245–282. [Google Scholar] [CrossRef]
- Vlakh, E.G.; Korzhikov, V.A.; Hubina, A.V.; Tennikova, T.B. Molecular imprinting: A tool of modern chemistry for the preparation of highly selective monolithic sorbents. Russ. Chem. Rev. 2015, 84, 952–980. [Google Scholar] [CrossRef]
- Vasiliev, N.K.; Pronk, A.D.C.; Shatalina, I.N.; Janssen, F.H.M.E.; Houben, R.W.G. A review on the development of reinforced ice for use as a building material in cold regions. Cold Reg. Sci. Technol. 2015, 115, 56–63. [Google Scholar] [CrossRef]
- Efremenko, E.N.; Lyagin, I.V.; Lozinsky, V.I. Enzymatic biocatalysts immobilized on/in the cryogel-type carriers. In Supermacroporous Cryogels: Biomedical and Biotechnological Applications; Kumar, A., Ed.; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group LLC.: Oxfordshire, UK, 2016; Chapter 11; pp. 301–324. ISBN 978-1-482-22881-6. [Google Scholar]
- Andaç, M.; Galaev, I.Y.; Denizli, A. Affinity based and molecularly imprinted cryogels: Application in biomacromolecule purification. J. Chromatogr. B. 2016, 1021, 69–80. [Google Scholar] [CrossRef]
- Hixon, K.R.; Lu, T.; Sell, S.A. A comprehensive review of cryogels and their roles in tissue engineering applications. Acta Biomaterialia 2017, 62, 29–41. [Google Scholar] [CrossRef]
- Gurikov, P.; Smirnova, I. Non-conventional methods for gelation of alginates. Gels 2018, 4, 14. [Google Scholar] [CrossRef] [Green Version]
- Wubneh, A.; Tsekoura, E.K.; Ayranci, C.; Uludağ, H. Current state of fabrication technologies and materials for bone tissue engineering. Acta Biomaterialia 2018, 80, 1–30. [Google Scholar] [CrossRef]
- Kudaibergenov, S.E. Physicochemical, complexation and catalytic properties of polyampholyte cryogels. Gels 2019, 5, 8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kudaibergenov, S.E.; Dzhardimalieva, G.I. Flow-through catalytic reactors based on metal nanoparticles immobilized within porous polymeric gels and surfaces/hollows of polymeric membranes. Polymers 2020, 12, 572. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nambu, M. Rubber-like poly(vinyl alcohol) gel. Kobunshi Ronbunshu 1990, 47, 695–703. [Google Scholar] [CrossRef]
- Peppas, N.A.; Stauffer, S.R. Reinforced uncross-linked poly(vinyl alcohol) gels produced by cyclic freezing-thawing processes: A short review. J. Contr. Release 1991, 16, 305–310. [Google Scholar] [CrossRef]
- Lozinsky, V.I. Cryotropic gelation of poly(vinyl alcohol). Russ. Chem. Rev. 1998, 67, 573–586. [Google Scholar] [CrossRef]
- Hassan, C.M.; Peppas, N.A. Structure and applications of poly(vinyl alcohol) hydrogels produced by conventional crosslinking or by freezing/thawing methods. Adv. Polym. Sci. 2000, 153, 37–65. [Google Scholar] [CrossRef]
- Gutiérrez, M.C.; Aranaz, I.; Ferrer, M.L.; del Monto, F. Production and properties of poly(vinyl alcohol) cryogels: Recent developments. In Macroporous Polymers: Production, Properties and Biological/Biomedical Applications; Mattiasson, B., Kumar, A., Galaev, I., Eds.; CRC Press: Boca Raton, FL, USA, 2010; pp. 83–115. ISBN 978-1-4200-8461-0. [Google Scholar]
- Lozinsky, V.I. A brief history of polymeric cryogels. Adv. Polym. Sci. 2014, 263, 1–48. [Google Scholar] [CrossRef]
- Ricciardi, R.; Auriemma, F.; De Rosa, C.; Di Girolamo, R. Investigation of the crystallinity of freeze/thaw hydrogels by different techniques. Macromolecules 2004, 37, 9510–9516. [Google Scholar] [CrossRef]
- De Rosa, C.; Auriemma, F.; Girolamo, R.D. Kinetic analysis of cryotropic gelation of poly(vinyl alcohol)/water solutions by small-angle neutron scattering. Adv. Polym. Sci. 2014, 263, 159–197. [Google Scholar] [CrossRef]
- Kobayashi, M.; Ando, I.; Ishii, T.; Amiya, S. Structural and dynamical studies of poly(vinyl alcohol) gels by high-resolution solid-state 13C NMR spectroscopy. J. Mol. Struct. 1998, 440, 155–164. [Google Scholar] [CrossRef]
- Kanekiyo, M.; Kobayashi, M.; Ando, I.; Kurosu, H.; Ishii, T.; Amiya, S. A structural and dynamic study of poly(vinyl alcohol) in the gel state by solid-state 13C NMR and 1H pulse NMR. J. Mol. Struct. 1998, 447, 49–59. [Google Scholar] [CrossRef]
- Lozinsky, V.I.; Vainerman, E.S.; Domotenko, L.V.; Mamtsis, A.M.; Titova, E.F.; Belavtseva, E.M.; Rogozhin, S.V. Study of cryostructurization of polymer systems. VII. Structure formation under freezing of poly(vinyl alcohol) aqueous solutions. Colloid Polym. Sci. 1986, 264, 19–24. [Google Scholar] [CrossRef]
- Yokoyama, F.; Masada, I.; Shimamura, K.; Ikawa, T.; Monobe, K. Morphology and structure of highly elastic poly(vinyl alcohol) hydrogel prepared by repeated freezing-and-melting. Colloid Polym. Sci. 1986, 264, 595–601. [Google Scholar] [CrossRef]
- Trieu, H.; Qutubuddin, S. Poly(vinyl alcohol) hydrogels. 2. Effects of processing parameters on structure and properties. Polymer 1995, 36, 2531–2539. [Google Scholar] [CrossRef]
- Mori, Y.; Tokura, H.; Yoshikawa, M. Properties of hydrogels synthesized by freezing and thawing aqueous poly(vinyl alcohol) solutions and their applications. J. Mater. Sci. 1997, 32, 491–496. [Google Scholar] [CrossRef]
- Willcox, P.J.; Howie, D.W.; Schmidt-Rohr, K.; Hoagland, D.A.; Gido, S.P.; Pudjijanto, S.; Kleiner, W.; Venkatraman, S. Microstructure of poly(vinyl alcohol) hydrogels produced by freeze/thaw cycling. J. Polym. Sci. B Polym. Phys. 1999, 37, 3438–3454. [Google Scholar] [CrossRef]
- Lozinsky, V.I.; Damshkaln, L.G.; Shaskol’skii, B.L.; Babushkina, T.A.; Kurochkin, I.N.; Kurochkin, I.I. Study of cryostructuring of polymer systems. 27. Physicochemical properties of poly(vinyl alcohol) cryogels and features of their macroporous morphology. Colloid, J. 2007, 69, 747–764. [Google Scholar] [CrossRef]
- Lozinsky, V.I.; Damshkaln, L.G.; Kurochkin, I.N.; Kurochkin, I.I. Study of cryostructuring of polymer systems. 28. Physicochemical properties and morphology of poly(vinyl alcohol) cryogels formed by multiple freezing-thawing. Colloid J. 2008, 70, 189–198. [Google Scholar] [CrossRef]
- Lozinsky, V.I.; Sakhno, N.G.; Damshkaln, L.G.; Bakeeva, I.V.; Zubov, V.P.; Kurochkin, I.N.; Kurochkin, I.I. Study of cryostructuring of polymer systems. 31. Influence of the additives of alkaline metals chlorides on physicochemical properties and morphology of poly(vinyl alcohol) cryogels. Colloid J. 2011, 73, 234–243. [Google Scholar] [CrossRef]
- Lozinsky, V.I.; Damshkaln, L.G.; Kurochkin, I.N.; Kurochkin, I.I. Study of cryostructuring of polymer systems. 33. Effect of rate of chilling aqueous poly(vinyl alcohol) solutions during their freezing on physicochemical properties and porous structure of resulting cryogels. Colloid J. 2012, 74, 319–327. [Google Scholar] [CrossRef]
- Lozinsky, V.I.; Damshkaln, L.G.; Kurochkin, I.N.; Kurochkin, I.I. Cryostructuring of polymeric systems. 36. Poly(vinyl alcohol) cryogels prepared from solutions of the polymer in water/low-molecular alcohol mixtures. Eur. Polym. J. 2014, 53, 189–205. [Google Scholar] [CrossRef]
- Asadi-Aghbolaghi, M.; Clapes, A.; Bellantonio, M.; Escalante, H.J.; Ponce-López, V.; Baró, X.; Escalera, S. A survey on deep learning based approaches for action and gesture recognition in image sequences. In Proceedings of the 2017 12th IEEE International Conference on Automatic Face & Gesture Recognition (FG 2017), Washington, DC, USA, 30 May–3 June 2017; pp. 476–483. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Chen, J.; Fieguth, P.; Zhao, G.; Chellappa, R.; Pietikäinen, M. From BoW to CNN: Two decades of texture representation for texture classification. Int. J. Comput. Vis. 2019, 127, 74–109. [Google Scholar] [CrossRef] [Green Version]
- Schmidhuber, J. Discovering neural nets with low Kolmogorov complexity and high generalization capability. Neural Netw. 1997, 10, 857–873. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Z.; Liu, X.; Zeng, N.; Liu, Y.; Alsaadi, F.E. A survey of deep neural network architectures and their applications. Neurocomputing 2017, 234, 11–26. [Google Scholar] [CrossRef]
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive subgradient methods for online learning and stochastic optimization. J. Mach. Learn. Res. 2011, 12, 2121–2159. [Google Scholar]
- Zhang, Z. Improved adam optimizer for deep neural networks. In Proceedings of the 2018 IEEE/ACM 26th International Symposium on Quality of Service (IWQoS), Banff, AB, Canada, 4–6 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–2. [Google Scholar] [CrossRef]
- Yuan, Z.W.; Zhang, J. Feature extraction and image retrieval based on AlexNet. In Proceedings of the Eighth International Conference on Digital Image Processing (ICDIP 2016), Chengu, China, 20–22 May 2016; Volume 10033, p. 100330E. [Google Scholar] [CrossRef]
- Marmanis, D.; Datcu, M.; Esch, T.; Stilla, U. Deep learning earth observation classification using ImageNet pre-trained networks. IEEE Geosci. Remote Sens. Lett. 2015, 13, 105–109. [Google Scholar] [CrossRef] [Green Version]
- Kieffer, B.; Babaie, M.; Kalra, S.; Tizhoosh, H.R. Convolutional neural networks for histopathology image classification: Training vs. using pre-trained networks. In Proceedings of the 2017 Seventh International Conference on Image Processing Theory, Tools and Applications (IPTA), Montreal, QC, Canada, 28 November–1 December 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Cavalin, P.; Oliveira, L.S. A review of texture classification methods and databases. In Proceedings of the 2017 30th SIBGRAPI Conference on Graphics, Patterns and Images Tutorials (SIBGRAPI-T), Niteroi, Brazil, 17–18 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–8. [Google Scholar] [CrossRef]
- Chaplin, M. Water Structure and Science. Available online: http://www1.lsbu.ac.uk/water/kosmotropes_chaotropes.html#r1567 (accessed on 29 August 2020).
- Kolosova, O.Y.; Kurochkin, I.N.; Kurochkin, I.I.; Lozinsky, V.I. Cryostructuring of polymeric systems. 48. Influence of organic non-ionic and ionic chaotropes or kosmotropes on the cryotropic gel-formation of aqueous poly(vinyl alcohol) solutions, as well as on the properties and microstructure of the resultant cryogels. Eur. Polym. J. 2018, 102, 169–177. [Google Scholar] [CrossRef]
- Segeev, G.B.; Batyuk, V.A. Reactions in frozen multicomponent systems. Russ. Chem. Rev. 1976, 45, 391–408. [Google Scholar] [CrossRef]
- Gusev, D.G.; Lozinsky, V.I.; Vainerman, E.S.; Bakhmutov, V.I. Study of the frozen water-poly(vinyl alcohol) system by 2H and 13C NMR spectroscopy. Magn. Reson. Chem. 1990, 28, 651–655. [Google Scholar] [CrossRef]
- Mikhalev, O.I.; Serpinski, M.; Lozinsky, V.I.; Kapanin, P.V.; Chkheidze, I.I.; Alfimov, M.V. Method for determination of liquid microphase volume: Application to the investigation of frozen H2O-poly(vinyl alcohol) system. Cryo-Letters 1991, 12, 197–206. [Google Scholar]
- Auriemma, F.; De Rosa, C.; Triolo, R. Slow crystallization kinetics of poly(vinyl alcohol) in confined environment during cryotropic gelation of aqueous solutions. Macromolecules 2006, 39, 9429–9434. [Google Scholar] [CrossRef]
- Timmermans, J. The Physico-Chemical Constants of Binary Systems in Concentrated Solutions; Interscience Publishers Inc.: New York, NY, USA, 1960; Volume 4. [Google Scholar]
- Hrouz, J.; Ilavsky, M.; Havliček, J.; Dušek, K. Comparison of the penetration, tensile and compression moduli of elasticity of poly(n-alkyl acrylate) networks in the rubberlike state. Collect. Czech. Chem. Comm. 1978, 43, 1999–2007. [Google Scholar] [CrossRef]
- Mark, J.E. The use of model polymer networks to elucidate molecular aspects of rubberlike elasticity. Adv. Polym. Sci. 1982, 44, 1–26. [Google Scholar] [CrossRef]
- Kazanskii, K.S.; Dubrovskii, S.A. Chemistry and physics of “agricultural” hydrogels. Adv. Polym. Sci. 1992, 104, 97–133. [Google Scholar] [CrossRef]
- Lozinsky, V.I.; Domotenko, L.V.; Vainerman, E.S.; Mamtsis, A.M.; Rogozhin, S.V. On the possibility of mechanodestruction of poly(vinyl alcohol) molecules under moderate freezing of its concentrated water solutions. Polym. Bull. 1986, 15, 333–340. [Google Scholar] [CrossRef]
- Nishinari, K.; Watase, M.; Tanaka, F. Structure of junction zones in poly(vinyl alcohol) gels by rheological and thermal studies. J. Chim. Phys. 1996, 93, 880–886. [Google Scholar] [CrossRef]
- Hatakeyema, T.; Uno, J.; Yamada, C.; Kishi, A.; Hatakeyama, H. Gel-sol transition of poly(vinyl alcohol) hydrogels formed by freezing and thawing. Thermochim. Acta 2005, 431, 144–148. [Google Scholar] [CrossRef]
- Eldridge, J.E.; Ferry, J.D. Studies of the cross-linking process in gelatin gels. III. Dependence of melting point on concentration and molecular weight. J. Phys. Chem. 1954, 58, 992–995. [Google Scholar] [CrossRef]
- Ross-Murphy, S.B.; McEvoy, H. Fundamentals of hydrogels and gelation. Brit. Polym. J. 1986, 18, 2–7. [Google Scholar] [CrossRef]
- Andrearczyk, V.; Whelan, P.F. Using filter banks in convolutional neural networks for texture classification. Pattern Recognit. Lett. 2016, 84, 63–69. [Google Scholar] [CrossRef]
- Kylberg, G. Kylberg Texture Dataset v. 1.0. Centre for Image Analysis, Swedish University of Agricultural Sciences and Uppsala University. 2011. Available online: http://www.cb.uu.se/~gustaf/texture/ (accessed on 29 August 2020).
- Akata, Z.; Perronnin, F.; Harchaoui, Z.; Schmid, C. Good practice in large-scale learning for image classification. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 36, 507–520. [Google Scholar] [CrossRef] [PubMed] [Green Version]





| Composition of Feed Solution | Physico-Mechanical | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Example Number | Low-Molecular Additive | Parameters | ||||||||
| PVA | Type | Charge | Substance | Concentration (mol/L) | Tcpa | G0 | G0ac/G0af | G20 | G20ac/G20af | |
| (g/L) | (°C) | (kPa) | (kPa) | |||||||
| 1a | 100 | - | - | none | - | −20 | 9.13 ± 0.40 | - | 5.77 ± 0.33 | - |
| b | - | - | - | −25 | 10.0 ± 0.80 | - | 6.20 ± 0.30 | - | ||
| c | - | - | - | −30 | 12.8 ± 0.30 | - | 11.1 ± 0.30 | - | ||
| d | - | - | - | −35 | 9.03 ± 0.21 | - | 6.94 ± 0.10 | - | ||
| 2a | chao- trope | non- ionic | URE | 0.05 | −20 | 6.41 ± 0.25 | 0.70 | 5.05 ± 0.11 | 0.88 | |
| b | 0.10 | 5.86 ± 0.16 | 0.64 | 4.93 ± 0.13 | 0.85 | |||||
| c | 0.20 | 3.17 ± 0.17 | 0.35 | 2.90 ± 0.08 | 0.50 | |||||
| d | 0.30 | 1.93 ± 0.13 | 0.21 | 1.29 ± 0.21 | 0.22 | |||||
| e | 0.40 | 1.67 ± 0.11 | 0.18 | ND | - | |||||
| f | 0.50 | 1.42 ± 0.12 | 0.16 | ND | - | |||||
| 3a | 0.05 | −25 | 6.21 ± 0.69 | 0.62 | 4.33 ± 0.41 | 0.70 | ||||
| b | 0.10 | 4.76 ± 0.10 | 0.48 | 3.79 ± 0.13 | 0.61 | |||||
| c | 0.20 | 3.54 ± 0.26 | 0.35 | 2.60 ± 0.28 | 0.42 | |||||
| d | 0.30 | 2.21 ± 0.19 | 0.22 | 1.58 ± 0.30 | 0.25 | |||||
| e | 0.40 | 1.65 ± 0.05 | 0.17 | 1.35 ± 0.13 | 0..22 | |||||
| f | 0.50 | 1.15 ± 0.09 | 0.12 | 1.04 ± 0.14 | 0.17 | |||||
| 4a | 0.05 | −30 | 5.01 ± 0.23 | 0.39 | 3.67 ± 0.39 | 0.33 | ||||
| b | 0.10 | 4.31 ± 0.25 | 0.34 | 3.60 ± 0.48 | 0.32 | |||||
| c | 0.20 | 3.14 ± 0.08 | 0.25 | 2.55 ± 0.15 | 0.23 | |||||
| d | 0.30 | 2.01 ± 0.15 | 0.16 | 1.50 ± 0.12 | 0.14 | |||||
| e | 0.40 | 1.57 ± 0.05 | 0.12 | 1.11 ± 0.15 | 0.10 | |||||
| f | 0.50 | 0.90 ± 0.10 | 0.07 | ND | - | |||||
| 5a | 0.05 | −35 | 8.67 ± 0.15 | 0.96 | 6.04 ± 0.20 | 0.87 | ||||
| b | 0.10 | 7.56 ± 0.80 | 0.83 | 4.93 ± 0.11 | 0.71 | |||||
| c | 0.20 | 6.25 ± 0.11 | 0.69 | 3.93 ± 0.19 | 0.57 | |||||
| d | 0.30 | 3.73 ± 0.09 | 0.41 | 2.80 ± 0.20 | 0.40 | |||||
| e | 0.40 | 3.05 ± 0.11 | 0.34 | 1.79 ± 0.13 | 0.26 | |||||
| f | 0.50 | 2.55 ± 0.15 | 0.28 | 1.71 ± 0.21 | 0.24 | |||||
| 6a | ionic | GHC | 0.05 | −20 | 5.57 ± 0.09 | 0.61 | 3.64 ± 0.08 | 0.63 | ||
| b | 0.10 | 3.83 ± 0.21 | 0.42 | 2.54 ± 0.08 | 0.44 | |||||
| c | 0.15 | 2.55 ± 0.07 | 0.28 | 1,79 ± 0.09 | 0.31 | |||||
| d | 0.20 | 2.06 ± 0.06 | 0.23 | 1.44 ± 0.12 | 0.25 | |||||
| e | 0.30 | ND | - | ND | - | |||||
| 7a | 0.05 | −25 | 7.35 ± 0.05 | 0.74 | 4.49 ± 0.47 | 0.72 | ||||
| b | 0.10 | 6.43 ± 0.09 | 0.64 | 3.35 ± 0.39 | 0.54 | |||||
| c | 0.15 | 3.86 ± 0.14 | 0.39 | 2.05 ± 0.31 | 0.33 | |||||
| d | 0.20 | 2.79 ± 0.07 | 0.28 | 1.49 ± 0.19 | 0.24 | |||||
| e | 0.25 | 2.00 ± 0.12 | 0.20 | 1.20 ± 0.12 | 0.19 | |||||
| f | 0.30 | 1.48 ± 0.04 | 0.15 | ND | - | |||||
| 8a | 100 | chao- trope | ionic | GHC | 0.05 | −30 | 8.08 ± 0.46 | 0.63 | 5.50 ± 0.18 | 0.50 |
| b | 0.10 | 7.11 ± 0.49 | 0.56 | 3.48 ± 0.40 | 0.31 | |||||
| c | 0.15 | 5.55 ± 0.51 | 0.43 | 2.88 ± 0.16 | 0.26 | |||||
| d | 0.20 | 4.20 ± 0.38 | 0.33 | 2.65 ± 0.15 | 0.24 | |||||
| e | 0.25 | 2.76 ± 0.20 | 0.22 | 1.86 ± 0.16 | 0.17 | |||||
| f | 0.30 | 2.29 ± 0.19 | 0.18 | 1.52 ± 0.18 | 0.14 | |||||
| 9a | 0.05 | −35 | 6.61 ± 0.09 | 0.73 | 4.65 ± 0.21 | 0.67 | ||||
| b | 0.10 | 4.52 ± 0.06 | 0.50 | 3.12 ± 0.30 | 0.45 | |||||
| c | 0.15 | 3.46 ± 0.04 | 0.38 | 2.59 ± 0.21 | 0.37 | |||||
| d | 0.20 | 2,29 ± 0.13 | 0.25 | 1.61 ± 0.25 | 0.23 | |||||
| e | 0.25 | 1.59 ± 0.11 | 0.18 | 1.25 ± 0.15 | 0.18 | |||||
| f | 0.30 | 1.22 ± 0.12 | 0.14 | ND | - | |||||
| 10a | kosmotrope | non-ionic | THL | 0.1 | −20 | 5.25 ± 0.59 | 0.58 | 4.40 ± 0.12 | 0.76 | |
| b | 0.2 | 4.85 ± 0.05 | 0.53 | 4.21 ± 0.07 | 0.73 | |||||
| c | 0.3 | 5.65 ± 0.15 | 0.62 | 4.38 ± 0.14 | 0.76 | |||||
| d | 0.5 | 7.40 ± 0.10 | 0.81 | 5.30 ± 0.10 | 0.92 | |||||
| e | 1.0 | 13.5 ± 0.60 | 1.48 | 10.0 ± 0.20 | 1.73 | |||||
| 11a | 0.1 | −25 | 7.40 ± 0.60 | 0.74 | 3.90 ± 0.10 | 0.63 | ||||
| b | 0.2 | 6.11 ± 0.29 | 0.61 | 3.70 ± 0.10 | 0.60 | |||||
| c | 0.3 | 7.32 ± 0.08 | 0.73 | 4.40 ± 0.12 | 0.71 | |||||
| d | 0.5 | 10.4 ± 0.20 | 1.04 | 6.04 ± 0.08 | 1.03 | |||||
| e | 1.0 | 16.7 ± 0.50 | 1.67 | 7.60 ± 0.10 | 1.23 | |||||
| 12a | 0.1 | −30 | 5.69 ± 0.19 | 0.44 | 5.27 ± 0.09 | 0.47 | ||||
| b | 0.2 | 5.80 ± 0.12 | 0.45 | 4.65 ± 0.21 | 0.42 | |||||
| c | 0.3 | 7.03 ± 0.21 | 0.55 | 4.51 ± 0.15 | 0.41 | |||||
| d | 0.5 | 11.7 ± 0.20 | 0.91 | 5.30 ± 0.28 | 0.45 | |||||
| e | 1.0 | 16.9 ± 0.90 | 1.32 | 10.0 ± 0.20 | 0.90 | |||||
| 13a | 0.1 | −35 | 7.88 ± 0.12 | 0.87 | 4.39 ± 0.21 | 0.63 | ||||
| b | 0.2 | 6.95 ± 0.45 | 0.77 | 3.07 ± 0.09 | 0.44 | |||||
| c | 0.3 | 6.90 ± 0.52 | 0.76 | 2.56 ± 0.40 | 0.37 | |||||
| d | 0.5 | 8.01 ± 0.87 | 0.89 | 4.39 ± 0.11 | 0.63 | |||||
| e | 1.0 | 15.0 ± 0.20 | 1.66 | 8.03 ± 0.29 | 1.16 | |||||
| 14a | ionic | HYP | 0.1 | −20 | 6.17 ± 0.32 | 0.68 | 4.80 ± 0.50 | 0.83 | ||
| b | 0.2 | 5.03 ± 0.35 | 0.55 | 4.65 ± 0.13 | 0.81 | |||||
| c | 0.3 | 5.98 ± 0.12 | 0.65 | 5.10 ± 0.22 | 0.88 | |||||
| d | 0.5 | 9.35 ± 1.03 | 1.02 | 7.00 ± 0.25 | 1.21 | |||||
| e | 1.0 | 12.4 ± 0.10 | 1.36 | 10.5 ± 0.50 | 1.82 | |||||
| 15a | 0.1 | −25 | 8.00 ± 0.12 | 0.80 | 5.05 ± 0.25 | 0.81 | ||||
| b | 0.2 | 6.68 ± 0.16 | 0.67 | 4.65 ± 0.11 | 0.75 | |||||
| c | 0.3 | 7.62 ± 0.10 | 0.76 | 5.27 ± 0.13 | 0.85 | |||||
| d | 0.5 | 10.7 ± 0.30 | 1.07 | 7.94 ± 0.32 | 1.28 | |||||
| e | 1.0 | 16.2 ± 0.40 | 1.62 | 12.4 ± 0.20 | 2.00 | |||||
| 16a | 100 | kosmotrope | ionic | HYP | 0.1 | −30 | 8.05 ± 0.21 | 0.63 | 5.27 ± 0.13 | 0.47 |
| b | 0.2 | 7.60 ± 0.40 | 0.59 | 4.93 ± 0.21 | 0.44 | |||||
| c | 0.3 | 9.30 ± 0.22 | 0.73 | 6.04 ± 0.20 | 0.54 | |||||
| d | 0.5 | 13.5 ± 0.40 | 1.05 | 9.08 ± 0.18 | 0.82 | |||||
| e | 1.0 | 18.1 ± 0.30 | 1.41 | 14.0 ± 0.20 | 1.26 | |||||
| 17a | 0.1 | −35 | 6.71 ± 0.11 | 0.74 | 4.50 ± 0.40 | 0.65 | ||||
| b | 0.2 | 6.62 ± 0.08 | 0.73 | 4.48 ± 0.12 | 0.65 | |||||
| c | 0.3 | 7.90 ± 0.60 | 0.87 | 4.65 ± 0.10 | 0.67 | |||||
| d | 0.5 | 8.40 ± 0.88 | 0.93 | 6.29 ± 0.11 | 0.91 | |||||
| e | 1.0 | 11.5 ± 0.50 | 1.27 | 6.80 ± 0.20 | 0.98 | |||||
| Name | Kosmo | Chao | Clear |
|---|---|---|---|
| Accuracy | 0.80 | 0.81 | 0.79 |
| Precision | 0.65 | 0.79 | 0.70 |
| Recall | 0.87 | 0.59 | 0.63 |
| F1-measure | 0.74 | 0.68 | 0.67 |
| Name | Kosmo | Chao | Clear |
|---|---|---|---|
| Accuracy | 0.97 | 0.95 | 0.98 |
| Precision | 0.84 | 0.65 | 0.79 |
| Recall | 0.76 | 0.58 | 1.00 |
| F1-measure | 0.8 | 0.61 | 0.88 |
| Name | Kosmo + Chao | Clear |
|---|---|---|
| Accuracy | 0.98 | 0.98 |
| Precision | 0.93 | 0.84 |
| Recall | 0.86 | 0.96 |
| F1-measure | 0.89 | 0.89 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kurochkin, I.I.; Kurochkin, I.N.; Kolosova, O.Y.; Lozinsky, V.I. Cryostructuring of Polymeric Systems †: Application of Deep Neural Networks for the Classification of Structural Features Peculiar to Macroporous Poly(vinyl alcohol) Cryogels Prepared without and with the Additives of Chaotropes or Kosmotropes. Molecules 2020, 25, 4480. https://doi.org/10.3390/molecules25194480
Kurochkin II, Kurochkin IN, Kolosova OY, Lozinsky VI. Cryostructuring of Polymeric Systems †: Application of Deep Neural Networks for the Classification of Structural Features Peculiar to Macroporous Poly(vinyl alcohol) Cryogels Prepared without and with the Additives of Chaotropes or Kosmotropes. Molecules. 2020; 25(19):4480. https://doi.org/10.3390/molecules25194480
Chicago/Turabian StyleKurochkin, Ilya I., Ilya N. Kurochkin, Olga Yu. Kolosova, and Vladimir I. Lozinsky. 2020. "Cryostructuring of Polymeric Systems †: Application of Deep Neural Networks for the Classification of Structural Features Peculiar to Macroporous Poly(vinyl alcohol) Cryogels Prepared without and with the Additives of Chaotropes or Kosmotropes" Molecules 25, no. 19: 4480. https://doi.org/10.3390/molecules25194480
APA StyleKurochkin, I. I., Kurochkin, I. N., Kolosova, O. Y., & Lozinsky, V. I. (2020). Cryostructuring of Polymeric Systems †: Application of Deep Neural Networks for the Classification of Structural Features Peculiar to Macroporous Poly(vinyl alcohol) Cryogels Prepared without and with the Additives of Chaotropes or Kosmotropes. Molecules, 25(19), 4480. https://doi.org/10.3390/molecules25194480