Inverse Solvent Isotope Effects in Enzyme-Catalyzed Reactions
Abstract
:1. Introduction
2. Theory of Solvent Isotope Effects
The Importance of pH Independence
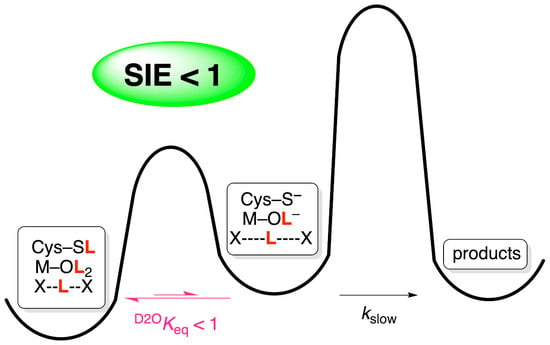
3. Cysteine Thiols
3.1. Cysteine Proteases: Papain and Cathepsin C
3.2. Protein Arginine Deiminase
3.3. Isocitrate Lyase
4. Metal-bound Water
4.1. Carbonic Anhydrase
4.2. Metal-Dependent Amidohydrolases: Thermolysin, Stromelysin, and Desuccinylase
4.3. Alcohol Dehydrogenase
4.4. Malate Synthase
4.5. Hypoxia-Inducible Factor-α (HIF) Hydroxylases: Prolyl Hydroxylase 2 (PDH2) and Factor-Inhibiting HIF (FIH)
4.6. Adenosine and AMP Deaminases
5. Low-Barrier Hydrogen Bonds
5.1. Aspartic Proteases
5.2. Alcohol Dehydrogenase
6. Medium Effects
6.1. β-Lactamase
6.2. Alkanesulfonate Monoxygenase
6.3. Glucokinase
7. Protein Conformational Changes
7.1. β-Lactam Synthetase
7.2. β-Ketoacyl Carrier Protein Reductase
8. Solvent Viscosity Effects vs. Solvent Isotope Effects
NAD-Malic Enzyme
9. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Schowen, B.K.; Schowen, R.L. Solvent isotope effects on enzyme systems. In Methods Enzymol; Purich, D.L., Ed.; Academic Press: Cambridge, MA, USA, 1982; Volume 87, pp. 551–606. [Google Scholar]
- Quinn, D. Theory and Practice of Solvent Isotope Effects. In Isotope Effects in Chemistry and Biology; Kohen, A., Limbach, H.-H., Eds.; CRC Press: Boca Raton, FL, USA, 2005; pp. 995–1018. [Google Scholar]
- Kresge, A.J.; Allred, A.L. Hydrogen Isotope Fractionation in Acidified Solutions of Protium and Deuterium Oxide. J. Am. Chem. Soc. 1963, 85, 1541. [Google Scholar] [CrossRef]
- Gold, V.; Grist, S. Deuterium solvent isotope effects on reactions involving the aqueous hydroxide ion. J. Chem. Soc. Perkin Trans. 1972, 2, 89–95. [Google Scholar] [CrossRef]
- Belasco, J.G.; Bruice, T.W.; Albery, W.J.; Knowles, J.R. Energetics of proline racemase: Fractionation factors for the essential catalytic groups in the enzyme-substrate complexes. Biochemistry 1986, 25, 2558–2564. [Google Scholar] [CrossRef]
- Jarret, R.M.; Saunders, M. A new method for obtaining isotopic fractionation data at multiple sites in rapidly exchanging systems. J. Am. Chem. Soc. 1985, 107, 2648–2654. [Google Scholar] [CrossRef]
- Salomaa, P.; Schaleger, L.L.; Long, F.A. Ionization of Some Weak Acids in Water—Heavy Water Mixtures1. J. Phys. Chem. 1964, 68, 410–411. [Google Scholar] [CrossRef]
- Kassebaum, J.W.; Silverman, D.N. Hydrogen/deuterium fractionation factors of the aqueous ligand of cobalt in Co(H2O)62+ and Co(II)-substituted carbonic anhydrase. J. Am. Chem. Soc. 1989, 111, 2691–2696. [Google Scholar] [CrossRef]
- Schneck, J.L.; Villa, J.P.; McDevitt, P.; McQueney, M.S.; Thrall, S.H.; Meek, T.D. Chemical Mechanism of a Cysteine Protease, Cathepsin C, As Revealed by Integration of both Steady-State and Pre-Steady-State Solvent Kinetic Isotope Effects. Biochemistry 2008, 47, 8697–8710. [Google Scholar] [CrossRef] [PubMed]
- Moynihan, M.M.; Murkin, A.S. Cysteine Is the General Base That Serves in Catalysis by Isocitrate Lyase and in Mechanism-Based Inhibition by 3-Nitropropionate. Biochemistry 2014, 53, 178–187. [Google Scholar] [CrossRef]
- Flagg, S.C.; Giri, N.; Pektas, S.; Maroney, M.J.; Knapp, M.J. Inverse Solvent Isotope Effects Demonstrate Slow Aquo Release from Hypoxia Inducible Factor-Prolyl Hydroxylase (PHD2). Biochemistry 2012, 51, 6654–6666. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Glasoe, P.K.; Long, F.A. Use of Glass Electrodes to Measure Acidities in Deuterium Oxide. J. Phys. Chem. 1960, 64, 188–190. [Google Scholar] [CrossRef]
- Cleland, W.W. Determining the Chemical Mechanisms of Enzyme-Catalyzed Reactions by Kinetic Studies. In Advances in Enzymology and Related Areas of Molecular Biology; Wiley: Hoboken, NJ, USA, 1977; Volume 45, pp. 273–387. [Google Scholar]
- Polgár, L. Deuterium Isotope Effects on Papain Acylation. Eur. J. Biochem. 1979, 98, 369–374. [Google Scholar] [CrossRef] [PubMed]
- Wandinger, A.; Creighton, D.J. Solvent isotope effects on the rates of alkylation of thiolamine models of papain. FEBS Lett. 1980, 116, 116–121. [Google Scholar] [CrossRef] [Green Version]
- Dreyton, C.J.; Knuckley, B.; Jones, J.E.; Lewallen, D.M.; Thompson, P.R. Mechanistic Studies of Protein Arginine Deiminase 2: Evidence for a Substrate-Assisted Mechanism. Biochemistry 2014, 53, 4426–4433. [Google Scholar] [CrossRef] [PubMed]
- Knuckley, B.; Bhatia, M.; Thompson, P.R. Protein Arginine Deiminase 4: Evidence for a Reverse Protonation Mechanism. Biochemistry 2007, 46, 6578–6587. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Weiss, P.M.; Cook, P.F.; Hermes, J.D.; Cleland, W.W. Evidence from nitrogen-15 and solvent deuterium isotope effects on the chemical mechanism of adenosine deaminase. Biochemistry 1987, 26, 7378–7384. [Google Scholar] [CrossRef] [PubMed]
- Creighton, D.J.; Schamp, D.J. Solvent isotope effects on tautomerization equilibria of papain and model thiolamines. FEBS Lett. 1980, 110, 313–318. [Google Scholar] [CrossRef] [Green Version]
- Zhai, X.; Meek, T.D. Catalytic Mechanism of Cruzain from Trypanosoma cruzi As Determined from Solvent Kinetic Isotope Effects of Steady-State and Pre-Steady-State Kinetics. Biochemistry 2018, 57, 3176–3190. [Google Scholar] [CrossRef]
- Ray, S.; Kreitler, D.F.; Gulick, A.M.; Murkin, A.S. The Nitro Group as a Masked Electrophile in Covalent Enzyme Inhibition. ACS Chem. Biol. 2018, 13, 1470–1473. [Google Scholar] [CrossRef]
- Steiner, H.; Jonsson, B.-H.; Lindskog, S. The Catalytic Mechanism of Carbonic Anhydrase. Eur. J. Biochem. 1975, 59, 253–259. [Google Scholar] [CrossRef]
- Stein, R.L. Transition-state structural features for the thermolysin-catalyzed hydrolysis of N-(3-[2-furyl]acryloyl)-Gly-LeuNH2. J. Am. Chem. Soc. 1988, 110, 7907–7908. [Google Scholar] [CrossRef]
- Izquierdo, M.C.; Stein, R.L. Mechanistic studies of thermolysin. J. Am. Chem. Soc. 1990, 112, 6054–6062. [Google Scholar] [CrossRef]
- Harrison, R.K.; Chang, B.; Niedzwiecki, L.; Stein, R.L. Mechanistic studies on the human matrix metalloproteinase stromelysin. Biochemistry 1992, 31, 10757–10762. [Google Scholar] [CrossRef]
- Born, T.L.; Zheng, R.; Blanchard, J.S. Hydrolysis of N-Succinyl-l,l-diaminopimelic Acid by the Haemophilus influenzae dapE-Encoded Desuccinylase: Metal Activation, Solvent Isotope Effects, and Kinetic Mechanism. Biochemistry 1998, 37, 10478–10487. [Google Scholar] [CrossRef]
- Welsh, K.M.; Creighton, D.J.; Klinman, J.P. Transition-state structure in the yeast alcohol dehydrogenase reaction: The magnitude of solvent and α-secondary hydrogen isotope effects. Biochemistry 1980, 19, 2005–2016. [Google Scholar] [CrossRef]
- Schmidt, J.; Chen, J.; DeTraglia, M.; Minkel, D.; McFarland, J.T. Solvent deuterium isotope effect on the liver alcohol dehydrogenase reaction. J. Am. Chem. Soc. 1979, 101, 3634–3640. [Google Scholar] [CrossRef]
- Quartararo, C.E.; Blanchard, J.S. Kinetic and Chemical Mechanism of Malate Synthase from Mycobacterium tuberculosis. Biochemistry 2011, 50, 6879–6887. [Google Scholar] [CrossRef] [Green Version]
- Hangasky, J.A.; Saban, E.; Knapp, M.J. Inverse Solvent Isotope Effects Arising from Substrate Triggering in the Factor Inhibiting Hypoxia Inducible Factor. Biochemistry 2013, 52, 1594–1602. [Google Scholar] [CrossRef] [Green Version]
- Merkler, D.J.; Schramm, V.L. Catalytic mechanism of yeast adenosine 5’-monophosphate deaminase. Zinc content, substrate specificity, pH studies, and solvent isotope effects. Biochemistry 1993, 32, 5792–5799. [Google Scholar] [CrossRef]
- Klinman, J.P. The mechanism of enzyme-catalyzed reduced nicotinamide adenine dinucleotide-dependent reductions. Substituent and isotope effects in the yeast alcohol dehydrogenase reaction. J. Biol. Chem. 1972, 247, 7977–7987. [Google Scholar]
- Wilson, D.K.; Rudolph, F.B.; Quiocho, F.A. Atomic structure of adenosine deaminase complexed with a transition-state analog: Understanding catalysis and immunodeficiency mutations. Science 1991, 252, 1278–1284. [Google Scholar] [CrossRef]
- Cleland, W.W. Low-barrier hydrogen bonds and low fractionation factor bases in enzymatic reactions. Biochemistry 1992, 31, 317–319. [Google Scholar] [CrossRef] [PubMed]
- Cleland, W.W.; Frey, P.A.; Gerlt, J.A. The Low Barrier Hydrogen Bond in Enzymatic Catalysis. J. Biol. Chem. 1998, 273, 25529–25532. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kreevoy, M.M.; Liang, T.M. Structures and isotopic fractionation factors of complexes, A1HA2. J. Am. Chem. Soc. 1980, 102, 3315–3322. [Google Scholar] [CrossRef]
- Rebholz, K.L.; Northrop, D.B. Slow step after bond-breaking by porcine pepsin identified using solvent deuterium isotope effects. Biochem. Biophys. Res. Commun. 1991, 176, 65–69. [Google Scholar] [CrossRef]
- Northrop, D.B. Follow the Protons: A Low-Barrier Hydrogen Bond Unifies the Mechanisms of the Aspartic Proteases. Acc. Chem. Res. 2001, 34, 790–797. [Google Scholar] [CrossRef]
- Raber, M.L.; Freeman, M.F.; Townsend, C.A. Dissection of the Stepwise Mechanism to β-Lactam Formation and Elucidation of a Rate-determining Conformational Change in β-Lactam Synthetase. J. Biol. Chem. 2009, 284, 207–217. [Google Scholar] [CrossRef] [Green Version]
- Sekhar, V.C.; Plapp, B.V. Rate constants for a mechanism including intermediates in the interconversion of ternary complexes by horse liver alcohol dehydrogenase. Biochemistry 1990, 29, 4289–4295. [Google Scholar] [CrossRef]
- Silva, R.G.; de Carvalho, L.P.S.; Blanchard, J.S.; Santos, D.S.; Basso, L.A. Mycobacterium tuberculosis β-Ketoacyl-Acyl Carrier Protein (ACP) Reductase: Kinetic and Chemical Mechanisms. Biochemistry 2006, 45, 13064–13073. [Google Scholar] [CrossRef]
- Pollard-Knight, D.; Cornish-Bowden, A. Solvent isotope effects on the glucokinase reaction. Eur. J. Biochem. 1984, 141, 157–163. [Google Scholar] [CrossRef]
- Pegan, S.D.; Rukseree, K.; Capodagli, G.C.; Baker, E.A.; Krasnykh, O.; Franzblau, S.G.; Mesecar, A.D. Active Site Loop Dynamics of a Class IIa Fructose 1,6-Bisphosphate Aldolase from Mycobacterium tuberculosis. Biochemistry 2013, 52, 912–925. [Google Scholar] [CrossRef] [Green Version]
- Adediran, S.A.; Deraniyagala, S.A.; Xu, Y.; Pratt, R.F. β-Secondary and Solvent Deuterium Kinetic Isotope Effects on β-Lactamase Catalysis. Biochemistry 1996, 35, 3604–3613. [Google Scholar] [CrossRef] [PubMed]
- Robbins, J.M.; Ellis, H.R. Steady-State Kinetic Isotope Effects Support a Complex Role of Arg226 in the Proposed Desulfonation Mechanism of Alkanesulfonate Monooxygenase. Biochemistry 2014, 53, 161–168. [Google Scholar] [CrossRef]
- Cleland, W.W. Low-Barrier Hydrogen Bonds and Enzymatic Catalysis. Arch. Biochem. Biophys. 2000, 382, 1–5. [Google Scholar] [CrossRef]
- Storer, A.C.; Cornish-Bowden, A. Kinetics of rat liver glucokinase. Co-operative interactions with glucose at physiologically significant concentrations. Biochem. J. 1976, 159, 7–14. [Google Scholar] [CrossRef] [Green Version]
- Parikh, S.; Moynihan, D.P.; Xiao, G.; Tonge, P.J. Roles of tyrosine 158 and lysine 165 in the catalytic mechanism of InhA, the enoyl-ACP reductase from Mycobacterium tuberculosis. Biochemistry 1999, 38, 13623–13634. [Google Scholar] [CrossRef]
- Cohen-Gonsaud, M.; Ducasse-Cabanot, S.; Quemard, A.; Labesse, G. Ligand-induced fit in mycobacterial MabA: The sequence-specific C-terminus locks the conformational change. Proteins 2005, 60, 392–400. [Google Scholar] [CrossRef]
- Karsten, W.E.; Lai, C.-J.; Cook, P.F. Inverse Solvent Isotope Effects in the NAD-Malic Enzyme Reaction Are the Result of the Viscosity Difference between D2O and H2O: Implications for Solvent Isotope Effect Studies. J. Am. Chem. Soc. 1995, 117, 5914–5918. [Google Scholar] [CrossRef]








| Exchangeable Group | ϕ | Reference |
|---|---|---|
| L3O+ | 0.69 | [3] |
| OL− | 0.43 | [4] |
| RSL (Cys) | 0.55 | [5] |
| ROL (Ser) | 1.04 | [6] |
| RCO2L (Asp, Glu) | 0.92 | [6] |
| RNL2 (His, Lys, Arg) | 1.13 | [6] |
| RNL3+ (His, Lys, Arg) | 1.08 | [7] |
| M–OL (M = Co2+) | 0.77 | [8] |
| M–OL2 (M = Co2+) | 0.81 | [8] |
| Enzyme | Varied Substrate/Agent | Inverse SKIE 1 | Reference |
|---|---|---|---|
| papain | Bz-Gly-OPh | D2Okac = 0.63 | [14] |
| Bz-Arg-NH2 | D2Okac = 0.58 | [14] | |
| Bz-Cit-NH2 | D2Okac = 0.46 | [14] | |
| Z-Phe-Gly-NH2 | D2Okac = 0.63 | [14] | |
| bromoacetamide | D2Okalk = 0.74 | [14] | |
| cysteine (papain model) | bromoacetate | D2Okalk = 0.70 ± 0.02 | [15] |
| chloroacetate | D2Okalk = 0.85 ± 0.10 | [15] | |
| bromoacetamide | D2Okalk = 0.69 ± 0.10 | [15] | |
| chloroacetamide | D2Okalk = 0.64 ± 0.04 | [15] | |
| methyl bromoacetate | D2Okalk = 0.53 ± 0.03 | [15] | |
| cathepsin C | Ser-Tyr-AMC | D2O(kcat/Km) = 0.71 ± 0.14 | [9] |
| protein arginine deiminase | Bz-Arg-OEt (PAD2) | D2O(kcat/Km) = 0.8 ± 0.1 | [16] |
| Bz-Arg-OEt (PAD4) | D2O(kcat/Km) = 0.43 | [17] | |
| isocitrate lyase | succinate | D2O(kcat/Km) = 0.56 ± 0.07 | [10] |
| adenosine deaminase | adenosine 7,8-dihydro-8-oxoadenosine | D2O(kcat/Km) = 0.77 ± 0.06 | [18] |
| D2O(kcat/Km) = 0.45 ± 0.04 | [18] |
| Enzyme Metal Cofactor | Varied Substrate/Condition | Inverse SKIE | Ref. |
|---|---|---|---|
| carbonic anhydrase C (esterase activity); Zn2+ | p-nitrophenyl acetate | D2O(kcat/Km) = 0.73 | [22] |
| thermolysin; Zn2+ | 3-(2-furyl)acrolyl-Gly-Leu-NH2 3-(2-furyl)acrolyl-Gly-Ala-NH2 3-(2-furyl)acrolyl-Gly-Abu-NH2 3-(2-furyl)acrolyl-Gly-Val-NH2 3-(2-furyl)acrolyl-Gly-Nva-NH2 3-(2-furyl)acrolyl-Gly-Phe-NH2 3-(2-furyl)acrolyl-Gly-Leu-NH2 3-(2-furyl)acrolyl-Gly-Leu-Ala | D2O(kcat/Km) = 0.80 ± 0.02 D2O(kcat/Km) = 0.80 ± 0.01 D2O(kcat/Km) = 0.73 ± 0.01 D2O(kcat/Km) = 0.76 ± 0.01 D2O(kcat/Km) = 0.73 ± 0.01 D2O(kcat/Km) = 0.73 ± 0.02 D2O(kcat/Km) = 0.69 ± 0.02 D2O(kcat/Km) = 0.72 ± 0.01 | [23] [24] [24] [24] [24] [24] [24] [24] |
| stromelysin; Zn2+ | pL 6.0 pL 7.5 pL 9.5 | D2O(kcat/Km) = 0.80 ± 0.03 D2O(kcat/Km) = 0.85 ± 0.06 D2O(kcat/Km) = 0.75 ± 0.02 | [25] [25] [25] |
| desuccinylase; Zn2+ | N-succinyl-L,L-diaminopimelate | D2O(kcat/Km) = 0.62 ± 0.06 | [26] |
| D2Okcat = 0.78 ± 0.05 | [26] | ||
| alcohol dehydrogenase; Zn2+ | NADH NADD | D2Okcat = 0.50 ± 0.05 D2Okcat = 0.58 ± 0.06 | [27] [27] |
| pL 8.75, single turnover | D2Okslow = 0.394 ± 0.005 | [28] | |
| malate synthase; Mg2+ | [methyl-2H3]acetyl-CoA | D2O(kcat/Km) = 0.6 ± 0.1 | [29] |
| prolyl hydroxylase 2; Fe2+ | acidic basic | D2Okcat = 0.91 ± 0.03 D2Okcat = 0.9 ± 0.1 | [11] [11] |
| factor-inhibiting hypoxia-inducible factor; Fe2+ | saturating CTAD, αKG CTAD αKG (high [CTAD]) αKG (low [CTAD]) | D2Okcat = 0.51 ± 0.07 D2O(kcat/Km) = 0.40 ± 0.07 D2O(kcat/Km) = 0.32 ± 0.08 D2O(kcat/Km) = 0.11 ± 0.03 | [30] [30] [30] [30] |
| adenosine deaminase; Zn2+ | adenosine 7,8-dihydro-8-oxoadenosine | D2O(kcat/Km) = 0.77 ± 0.06 D2O(kcat/Km) = 0.45 ± 0.04 | [18] [18] |
| AMP deaminase; Zn2+ | AMP, no ATP | D2O(kcat/Km) = 0.71 ± 0.07 | [31] |
| D2Okcat = 0.98 ± 0.04 | [31] | ||
| AMP, 0.1 mM ATP | D2O(kcat/Km) = 0.79 ± 0.11 | [31] | |
| D2Okcat = 0.75 ± 0.03 | [31] | ||
| 2′-dAMP, no ATP | D2O(kcat/Km) = 0.49 ± 0.04 | [31] | |
| D2Okcat = 0.62 ± 0.02 | [31] | ||
| 2′-dAMP, 0.1 mM ATP | D2O(kcat/Km) = 0.34 ± 0.02 | [31] | |
| D2Okcat = 0.63 ± 0.02 | [31] | ||
| 8-Br-AMP, 0.1 mM ATP | D2O(kcat/Km) = 0.33 ± 0.03 | [31] | |
| D2Okcat = 0.58 ± 0.03 | [31] |
| Enzyme | Substrate | Inverse SKIE | Ref. |
|---|---|---|---|
| pepsin | Leu-Ser-(p-NO2)-Phe-Nle-Ala-Leu-OMe | D2O(kcat/Km) = 0.84 ± 0.21 | [37] |
| HIV-1 protease | D2O(kcat/Km) = 0.85 ± 0.09 | [38] | |
| β-lactam synthetase | N2-(2-carboxyethyl)-l-arginine | D2O(kcat/Km) = 0.67 ± 0.15 | [39] |
| alcohol dehydrogenase | ethanol, saturating NAD+ | D2O(kobs) = 0.50 1 | [40] |
| ACP reductase | AcAcSCoA, NADPD | D2O(kcat/Km) = 0.58 | [41] |
| glucokinase | glucose, low ATP glucose, high ATP | D2O(kcat/Km) = 0.22 D2O(kcat/Km) = 0.29 | [42] [42] |
| fructose 1,6-bisphosphate aldolase | WT E168A D276A | D2O(kcat/Km) = 0.94 ± 0.07 D2O(kcat/Km) = 0.61 ± 0.07 D2O(kcat/Km) = 0.79 ± 0.06 | [43] [43] [43] |
| TEM (class A β-lactamase) | depsipeptide, 2 pL 7.0 depsipeptide, 2 pL 7.5 depsipeptide, 2 pL 8.0 | D2O(kcat/Km) = 0.72 ± 0.03 D2O(kcat/Km) = 0.70 ± 0.02 D2O(kcat/Km) = 0.61 ± 0.02 | [44] [44] [44] |
| P99 (class C, β-lactamase) | depsipeptide, 2 pL 7.5 | D2O(kcat/Km) = 0.79 ± 0.01 3 D2O(kcat/Km) = 0.85 ± 0.01 3 | [44] [44] |
| alkanesulfate monooxygenase | 1-octanesulfonate | D2O(kcat/Km) = 0.95 ± 0.07 | [45] |
| D2O(kcat) = 0.75 ± 0.04 | [45] | ||
| 1-[1,1-2H2]-octanesulfonate | D2O(kcat/Km) = 0.83 ± 0.17 | [45] | |
| D2O(kcat) = 0.79 ± 0.07 | [45] |
| Substrate | Fixed Substrate, Cofactor(s) | SKIE | Solvent Viscosity Effect 2 | ||
|---|---|---|---|---|---|
| D2O(kcat/Km) | D2Okcat | kcat/Km | kcat | ||
| malate | NAD+, Mg2+ | 0.5 ± 0.1 | 0.76 ± 0.02 | 0.6 ± 0.2 | 0.85 ± 0.07 |
| NAD+, Cd2+ | 0.37 ± 0.06 | 1.0 ± 0.2 | 0.61 ± 0.02 | 0.86 ± 0.08 | |
| NAD+, Mn2+ | 0.5 ± 0.3 | 1.272 ± 0.006 | 0.62 ± 0.05 | 1.0 ± 0.1 | |
| NAD+, Mg2+, fumarate | 0.47 ± 0.07 | 0.80 ± 0.02 | 0.46 ± 0.03 | 0.84 ± 0.01 | |
| APAD, 3 Mg2+ | 0.49 ± 0.06 | 0.91 ± 0.02 | 0.62 ± 0.06 | 0.82 ± 0.06 | |
| APAD, Mn2+ | 0.76 ± 0.03 | 0.99 ± 0.01 | 0.57 ± 0.01 | 0.78 ± 0.04 | |
| APAD, Mn2+, fumarate | 0.81 ± 0.03 | 1.07 ± 0.02 | 0.68 ± 0.02 | 0.85 ± 0.03 | |
| NAD+ | malate, Mg2+ | 0.57 ± 0.02 | 0.81 ± 0.06 | 0.689 ± 0.001 | 0.891 ± 0.001 |
| pyruvate | NADH, CO2, Mg2+ | 0.42 ± 0.01 | 0.35 ± 0.08 | 0.41 ± 0.02 | 0.44 ± 0.07 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernandez, P.L.; Murkin, A.S. Inverse Solvent Isotope Effects in Enzyme-Catalyzed Reactions. Molecules 2020, 25, 1933. https://doi.org/10.3390/molecules25081933
Fernandez PL, Murkin AS. Inverse Solvent Isotope Effects in Enzyme-Catalyzed Reactions. Molecules. 2020; 25(8):1933. https://doi.org/10.3390/molecules25081933
Chicago/Turabian StyleFernandez, Patrick L., and Andrew S. Murkin. 2020. "Inverse Solvent Isotope Effects in Enzyme-Catalyzed Reactions" Molecules 25, no. 8: 1933. https://doi.org/10.3390/molecules25081933
APA StyleFernandez, P. L., & Murkin, A. S. (2020). Inverse Solvent Isotope Effects in Enzyme-Catalyzed Reactions. Molecules, 25(8), 1933. https://doi.org/10.3390/molecules25081933