Force Field Parameters for Fe2+4S2−4 Clusters of Dihydropyrimidine Dehydrogenase, the 5-Fluorouracil Cancer Drug Deactivation Protein: A Step towards In Silico Pharmacogenomics Studies
Abstract
:1. Introduction
1.1. DPD Structure and Mechanism of Action
1.2. The Study
2. Results and Discussion
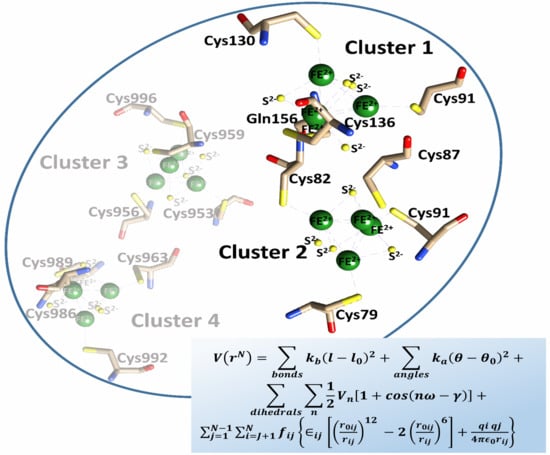
2.1. Human DPD 3D Wild Type (WT) Complete Structure Determined via Homology Modeling Approaches
2.2. AMBER Force Field Parameters Generated Using Bonded Approaches
2.2.1. Geometry Optimization
2.2.2. RESP Charges
2.2.3. Inferring the Generated QM Force Fields Parameters to the Corresponding Identical Clusters
2.3. Genereted Force Field Parameters Validated Using MD Simulations
2.3.1. Analysis of Protein Stability and Flexibility through RMSD, RMSF, and Rg
2.3.2. Fe2+4S2−4 Clusters Exhibited Stability during MD Simulations
2.3.3. Validation of Derived Parameters in IH7X Crystal Structure
2.4. Essential Motions of Protein in Phase Space
3. Materials and Methods
3.1. Software
3.2. Homology Modeling of Native DPD Protein.
3.3. Protonation of Titrarable Residues.
3.4. New Force Field Parameter Generation.
3.5. Force Field Parameters Validation and Analysis
3.5.1. Root Mean Square, Root Mean Square Fluctuation, and Radius of Gyration Analysis
3.5.2. Principal Component Analysis
3.5.3. Additional Analytical Approaches
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
Abbreviations
| 3D | Three-dimensional |
| 5-FU | Five-fluorouracil |
| ACPYPE | Ante-Chamber Python Parser interface |
| CHPC | Center for high performance computing |
| CPU | Central processing unit |
| DPD | Dihydropyrimidine dehydrogenase |
| FAD | Flavin adenine dinucleotide |
| FMN | Flavin mononucleotide |
| MCBP | Metal center parameter builder |
| MD | Molecular dynamics |
| MM | Molecular mechanics |
| NADP | Nicotinamide adenine dinucleotide phosphate |
| PBC | Periodic boundary conditions |
| PDB | Protein Data bank |
| PME | Particle mesh Ewald |
| RESP | Restricted electrostatic potential |
| QM | Quantum mechanics |
| URF | Five fluorouracil |
| VFFDT | Visual force field derivation toolkit |
| WT | Wild type |
References
- Dobritzsch, D.; Ricagno, S.; Schneider, G.; Schnackerz, K.D.; Lindqvist, Y. Crystal Structure of the Productive Ternary Complex of Dihydropyrimidine Dehydrogenase with NADPH and 5-Iodouracil. J. Biol. Chem. 2002, 277, 13155–13166. [Google Scholar] [CrossRef] [Green Version]
- Dobritzsch, R.; Schneider, G.; Schnackerz, K.D.; Lindqvist, Y. Crystal structure of dihydropyrimidine dehydrogenase, a major determinant of the pharmacokinetics of the anti-cancer drug 5-fluorouracil. EMBO J. 2001, 20, 650–660. [Google Scholar] [CrossRef] [Green Version]
- Miteva-Marcheva, N.N.; Ivanov, H.Y.; Dimitrov, D.K.; Stoyanova, V.K. Application of pharmacogenetics in oncology. Biomark. Res. 2020, 8, 1–10. [Google Scholar] [CrossRef]
- Mazzuca, F.; Borro, M.; Botticelli, A.; Mazzotti, E.; Marchetti, L.; Gentile, G.; La Torre, M.; Lionetto, L.; Simmaco, M.; Marchetti, P. Pre-treatment evaluation of 5-fluorouracil degradation rate: Association of poor and ultra-rapid metabolism with severe toxicity in a colorectal cancer patients cohort. Oncotarget 2016, 7, 20612–20620. [Google Scholar] [CrossRef] [Green Version]
- Wigle, T.J.; Tsvetkova, E.V.; Welch, S.A.; Kim, R.B. DPYD and Fluorouracil-Based Chemotherapy: Mini Review and Case Report. Pharmaceutics 2019, 11, 199. [Google Scholar] [CrossRef] [Green Version]
- García-González, X.; Kaczmarczyk, B.; Abarca-Zabalía, J.; Thomas, F.; García-Alfonso, P.; Robles, L.; Pachón, V.; Vaz, Á.; Salvador-Martín, S.; Sanjurjo-Sáez, M.; et al. New DPYD variants causing DPD deficiency in patients treated with fluoropyrimidine. Cancer Chemother. Pharmacol. 2020, 86, 45–54. [Google Scholar] [CrossRef] [PubMed]
- Tozer, T.; Heale, K.; Chagas, C.M.; Barros, A.L.B.; Alisaraie, L. Interdomain twists of human thymidine phosphorylase and its active–inactive conformations: Binding of 5-FU and its analogues to human thymidine phosphorylase versus dihydropyrimidine dehydrogenase. Chem. Biol. Drug Des. 2019, 94, 1956–1972. [Google Scholar] [CrossRef] [PubMed]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The Protein Data Bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mander, L.; Liu, H.-W. Comprehensive Natural Products II: Chemistry and Biology; Elsevier: Oxford, UK, 2010; Volume 3, pp. 205–236. [Google Scholar]
- Fagan, R.L.; Palfey, B.A. Flavin-Dependent Enzymes; Elsevier Ltd.: New York, NY, USA, 2010; pp. 38–43. [Google Scholar]
- Schnackerz, K.D.; Dobritzsch, D.; Lindqvist, Y.; Cook, P.F. Dihydropyrimidine dehydrogenase: A flavoprotein with four iron–sulfur clusters. Biochim. Biophys. Acta (BBA) Proteins Proteom. 2004, 1701, 61–74. [Google Scholar] [CrossRef]
- Lohkamp, B.; Voevodskaya, N.; Lindqvist, Y.; Dobritzsch, D. Insights into the mechanism of dihydropyrimidine dehydrogenase from site-directed mutagenesis targeting the active site loop and redox cofactor coordination. Biochim. Biophys. Acta (BBA) Proteins Proteom. 2010, 1804, 2198–2206. [Google Scholar] [CrossRef]
- Podschun, B.; Wahler, G.; Schnackerz, K.D. Purification and characterization of dihydropyrimidine dehydrogenase from pig liver. JBIC J. Biol. Inorg. Chem. 1989, 185, 219–224. [Google Scholar] [CrossRef]
- Podschun, B.; Cook, P.F.; Schnackerz, K.D. Kinetic mechanism of dihydropyrimidine dehydrogenase from pig liver. J. Biol. Chem. 1990, 265, 12966–12972. [Google Scholar] [CrossRef]
- Dudev, T.; Lim, C. Metal Binding Affinity and Selectivity in Metalloproteins: Insights from Computational Studies. Annu. Rev. Biophys. 2008, 37, 97–116. [Google Scholar] [CrossRef] [PubMed]
- Ziller, A.; Yadav, R.K.; Capdevila, M.; Reddy, M.S.; Vallon, L.; Marmeisse, R.; Atrian, S.; Palacios, Ò.; Fraissinet-Tachet, L. Metagenomics analysis reveals a new metallothionein family: Sequence and metal-binding features of new environmental cysteine-rich proteins. J. Inorg. Biochem. 2017, 167, 1–11. [Google Scholar] [CrossRef]
- Jing, Z.; Liu, C.; Qi, R.; Ren, P. Many-body effect determines the selectivity for Ca2+ and Mg2+ in proteins. Proc. Natl. Acad. Sci. USA 2018, 115, E7495–E7501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Valasatava, Y.; Rosato, A.; Furnham, N.; Thornton, J.M.; Andreini, C. To what extent do structural changes in catalytic metal sites affect enzyme function? J. Inorg. Biochem. 2018, 179, 40–53. [Google Scholar] [CrossRef]
- Barber-Zucker, S.; Shaanan, B.; Zarivach, R. Transition metal binding selectivity in proteins and its correlation with the phylogenomic classification of the cation diffusion facilitator protein family. Sci. Rep. 2017, 7, 16381. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lopes, P.E.M.; Guvench, O.; MacKerell, A.D. Current Status of Protein Force Fields for Molecular Dynamics Simulations. Methods Mol. Biol. 2015, 1215, 47–71. [Google Scholar] [CrossRef] [Green Version]
- Robustelli, P.; Piana, S.; Shaw, D.E. Developing a molecular dynamics force field for both folded and disordered protein states. Proc. Natl. Acad. Sci. USA 2018, 115, E4758–E4766. [Google Scholar] [CrossRef] [Green Version]
- Singh, S.; Singh, V.K. Molecular Dynamics Simulation: Methods and Application. In Frontiers in Protein Structure, Function, and Dynamics; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2020; pp. 213–238. [Google Scholar]
- Shi, W.; Chance, M.R. Metalloproteomics: Forward and reverse approaches in metalloprotein structural and functional characterization. Curr. Opin. Chem. Biol. 2011, 15, 144–148. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Musyoka, T.; Bishop, Ö.T.; Lobb, K.; Moses, V. The determination of CHARMM force field parameters for the Mg2+ containing HIV-1 integrase. Chem. Phys. Lett. 2018, 711, 1–7. [Google Scholar] [CrossRef]
- Bray, S.; Furriols, M. Notch pathway: Making sense of Suppressor of Hairless. Curr. Biol. 2001, 11, R217–R221. [Google Scholar] [CrossRef] [Green Version]
- Carloni, P.; Rothlisberger, U.; Parrinello, M. The Role and Perspective of Ab Initio Molecular Dynamics in the Study of Biological Systems. Accounts Chem. Res. 2002, 35, 455–464. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Merz, J.K.M. Metal Ion Modeling Using Classical Mechanics. Chem. Rev. 2017, 117, 1564–1686. [Google Scholar] [CrossRef] [PubMed]
- Durell, S.R.; Brooks, B.R.; Ben-Naim, A. Solvent-Induced Forces between Two Hydrophilic Groups. J. Phys. Chem. 1994, 98, 2198–2202. [Google Scholar] [CrossRef]
- Oostenbrink, C.; Villa, A.; Mark, A.E.; Van Gunsteren, W.F. A biomolecular force field based on the free enthalpy of hydration and solvation: The GROMOS force-field parameter sets 53A5 and 53A6. J. Comput. Chem. 2004, 25, 1656–1676. [Google Scholar] [CrossRef]
- Best, R.B.; Zhu, X.; Shim, J.; Lopes, P.E.M.; Mittal, J.; Feig, M.; MacKerell, J.A.D. Optimization of the Additive CHARMM All-Atom Protein Force Field Targeting Improved Sampling of the Backbone ϕ, ψ and Side-Chain χ1 and χ2 Dihedral Angles. J. Chem. Theory Comput. 2012, 8, 3257–3273. [Google Scholar] [CrossRef] [Green Version]
- MacKerell, A.D.; Bashford, D.; Bellott, M.; Dunbrack, R.L.; Evanseck, J.D.; Field, M.J.; Fischer, S.; Gao, J.; Guo, H.; Ha, S.; et al. All-Atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [Google Scholar] [CrossRef]
- Cornell, W.D.; Cieplak, P.; Bayly, C.I.; Gould, I.R.; Merz, K.M.; Ferguson, D.M.; Spellmeyer, D.C.; Fox, T.; Caldwell, J.W.; Kollman, P.A. A Second Generation Force Field for the Simulation of Proteins, Nucleic Acids, and Organic Molecules. J. Am. Chem. Soc. 1995, 117, 5179–5197. [Google Scholar] [CrossRef] [Green Version]
- Guvench, O.; MacKerell, A.D., Jr. Comparison of Protein Force Fields for Molecular Dynamics Simulations. Adv. Struct. Saf. Stud. 2008, 443, 63–88. [Google Scholar] [CrossRef]
- Vanommeslaeghe, K.; Guvench, O. Molecular mechanics. Curr. Pharm. Des. 2014, 20, 3281–3292. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kaminski, G.A.; Friesner, R.A.; Tirado-Rives, J.; Jorgensen, W.L. Evaluation and Reparametrization of the OPLS-AA Force Field for Proteins via Comparison with Accurate Quantum Chemical Calculations on Peptides. J. Phys. Chem. B 2001, 105, 6474–6487. [Google Scholar] [CrossRef]
- Price, M.L.P.; Ostrovsky, D.; Jorgensen, W.L. Gas-phase and liquid-state properties of esters, nitriles, and nitro compounds with the OPLS-AA force field. J. Comput. Chem. 2001, 22, 1340–1352. [Google Scholar] [CrossRef]
- Mohamadi, F.; Richards, N.G.J.; Guida, W.C.; Liskamp, R.; Lipton, M.; Caufield, C.; Chang, G.; Hendrickson, T.; Still, W.C. Macromodel?an integrated software system for modeling organic and bioorganic molecules using molecular mechanics. J. Comput. Chem. 1990, 11, 440–467. [Google Scholar] [CrossRef]
- Vanommeslaeghe, K.; Hatcher, E.; Acharya, C.; Kundu, S.; Zhong, S.; Shim, J.; Darian, E.; Guvench, O.; Lopes, P.; Vorobyov, I.; et al. CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput. Chem. 2009, 31, 671–690. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, W.; He, X.; Vanommeslaeghe, K.; MacKerell, A.D. Extension of the CHARMM general force field to sulfonyl-containing compounds and its utility in biomolecular simulations. J. Comput. Chem. 2012, 33, 2451–2468. [Google Scholar] [CrossRef] [Green Version]
- Vanommeslaeghe, K.; MacKerell, A.D. Automation of the CHARMM General Force Field (CGenFF) I: Bond Perception and Atom Typing. J. Chem. Inf. Model. 2012, 52, 3144–3154. [Google Scholar] [CrossRef]
- Vanommeslaeghe, K.; Raman, E.P.; MacKerell, A.D. Automation of the CHARMM General Force Field (CGenFF) II: Assignment of Bonded Parameters and Partial Atomic Charges. J. Chem. Inf. Model. 2012, 52, 3155–3168. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef] [PubMed]
- Hancock, R.D. Molecular mechanics calculations and metal ion recognition. Accounts Chem. Res. 1990, 23, 253–257. [Google Scholar] [CrossRef]
- Stote, R.H.; Karplus, M. Zinc binding in proteins and solution. a simple but accurate nonbonded representation. Proteins 1995, 23, 12–31. [Google Scholar] [CrossRef] [PubMed]
- Case, D.; Darden, T.; Cheatham, T.; Simmerling, C.; Wang, J.; Duke, R.; Luo, R.; Crowley, M.; Walker, R.; Zhang, W. AMBER 12. University of California, San Francisco; University of California, San Francisco: San Francisco, CA, USA, 2012. [Google Scholar]
- Li, P.; Merz, J.K.M. MCPB.py: A Python Based Metal Center Parameter Builder. J. Chem. Inf. Model. 2016, 56, 599–604. [Google Scholar] [CrossRef]
- Pang, Y.P. Novel Zinc Protein Molecular Dynamics Simulations: Steps Toward Antiangiogenesis for Cancer Treatment. J. Mol. Model. 1999, 5, 196–202. [Google Scholar] [CrossRef]
- Åqvist, J. Modelling of ion-ligand interactions in solutions and biomolecules. J. Mol. Struct. THEOCHEM 1992, 256, 135–152. [Google Scholar] [CrossRef]
- Sakharov, D.V.; Lim, C. Zn Protein Simulations Including Charge Transfer and Local Polarization Effects. J. Am. Chem. Soc. 2005, 127, 4921–4929. [Google Scholar] [CrossRef]
- Peraro, M.D.; Spiegel, K.; Lamoureux, G.; De Vivo, M.; DeGrado, W.F.; Klein, M.L. Modeling the charge distribution at metal sites in proteins for molecular dynamics simulations. J. Struct. Biol. 2007, 157, 444–453. [Google Scholar] [CrossRef] [PubMed]
- Zhu, T.; Xiao, X.; Ji, C.; Zhang, J.Z.H. A New Quantum Calibrated Force Field for Zinc–Protein Complex. J. Chem. Theory Comput. 2013, 9, 1788–1798. [Google Scholar] [CrossRef]
- Teixeira, M.H.; Curtolo, F.; Camilo, S.R.G.; Field, M.J.; Zheng, P.; Li, H.; Arantes, G.M. Modeling the Hydrolysis of Iron–Sulfur Clusters. J. Chem. Inf. Model. 2019, 60, 653–660. [Google Scholar] [CrossRef]
- Oda, A.; Yamaotsu, N.; Hirono, S. New AMBER force field parameters of heme iron for cytochrome P450s determined by quantum chemical calculations of simplified models. J. Comput. Chem. 2005, 26, 818–826. [Google Scholar] [CrossRef]
- Carvalho, A.T.P.; Teixeira, A.F.S.; Ramos, M.J. Parameters for molecular dynamics simulations of iron-sulfur proteins. J. Comput. Chem. 2013, 34, 1540–1548. [Google Scholar] [CrossRef]
- Sheik Amamuddy, O.S.; Musyoka, T.M.; Boateng, R.A.; Zabo, S.; Bishop, Ö.T. Determining the unbinding events and conserved motions associated with the pyrazinamide release due to resistance mutations of Mycobacterium tuberculosis pyrazinamidase. Comput. Struct. Biotechnol. J. 2020, 18, 1103–1120. [Google Scholar] [CrossRef] [PubMed]
- Seminario, J.M. Calculation of intramolecular force fields from second-derivative tensors. Int. J. Quantum Chem. 1996, 60, 1271–1277. [Google Scholar] [CrossRef]
- Zheng, S.; Tang, Q.; He, J.; Du, S.; Xu, S.; Wang, C.; Xu, Y.; Lin, F. VFFDT: A New Software for Preparing AMBER Force Field Parameters for Metal-Containing Molecular Systems. J. Chem. Inf. Model. 2016, 56, 811–818. [Google Scholar] [CrossRef] [PubMed]
- Kelm, S.; Shi, J.; Deane, C.M. MEDELLER: Homology-based coordinate generation for membrane proteins. Bioinformatics 2010, 26, 2833–2840. [Google Scholar] [CrossRef] [Green Version]
- BIOVIA, Dassault Systèmes. Discovery Studio Modeling Environment, Release 2019; Dassault Systèmes: San Diego, CA, USA, 2019. [Google Scholar]
- Shen, M.-Y.; Sali, A. Statistical potential for assessment and prediction of protein structures. Protein Sci. 2006, 15, 2507–2524. [Google Scholar] [CrossRef] [Green Version]
- Eramian, D.; Eswar, N.; Shen, M.-Y.; Sali, A. How well can the accuracy of comparative protein structure models be predicted? Protein Sci. 2008, 17, 1881–1893. [Google Scholar] [CrossRef] [Green Version]
- Eisenberg, D.; Lüthy, R.; Bowie, J.U. VERIFY3D: Assessment of protein models with three-dimensional profiles. Methods Enzymol. 1997, 277, 396–404. [Google Scholar] [CrossRef]
- Benkert, P.; Künzli, M.; Schwede, T. QMEAN server for protein model quality estimation. Nucleic Acids Res. 2009, 37, W510–W514. [Google Scholar] [CrossRef] [Green Version]
- Wiederstein, M.; Sippl, M.J. ProSA-web: Interactive web service for the recognition of errors in three-dimensional structures of proteins. Nucleic Acids Res. 2007, 35 (Suppl. 2), W407–W410. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Laskowski, R.A.; MacArthur, M.W.; Thornton, J.M. Validation of protein models derived from experiment. Curr. Opin. Struct. Biol. 1998, 8, 631–639. [Google Scholar] [CrossRef]
- Van Der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J.C. GROMACS: Fast, flexible, and free. J. Comput. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef] [PubMed]
- Anandakrishnan, R.; Aguilar, B.; Onufriev, A.V. H++ 3.0: Automating pK prediction and the preparation of biomolecular structures for atomistic molecular modeling and simulations. Nucleic Acids Res. 2012, 40, W537–W541. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bowers, K.J.; Sacerdoti, F.D.; Salmon, J.K.; Shan, Y.; Shaw, D.E.; Chow, E.; Xu, H.; Dror, R.O.; Eastwood, M.P.; Gregersen, B.A.; et al. Molecular Dynamics-Scalable Algorithms for Molecular Dynamics Simulations on Commodity Clusters. In Proceedings of the 2006 ACM/IEEE Conference on Supercomputing, Tampa, FL, USA, 11–17 November 2006; p. 84. [Google Scholar]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Semiempirical hybrid density functional with perturbative second-order correlation. J. Chem. Phys. 2006, 124, 034108. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Weaver, M.N.; Merz, J.K.M. Assessment of the “6-31+G** + LANL2DZ” Mixed Basis Set Coupled with Density Functional Theory Methods and the Effective Core Potential: Prediction of Heats of Formation and Ionization Potentials for First-Row-Transition-Metal Complexes. J. Phys. Chem. A 2009, 113, 9843–9851. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bannwarth, C.; Ehlert, S.; Grimme, S. GFN2-xTB—An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions. J. Chem. Theory Comput. 2019, 15, 1652–1671. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grimme, S.; Bannwarth, C.; Shushkov, P. A Robust and Accurate Tight-Binding Quantum Chemical Method for Structures, Vibrational Frequencies, and Noncovalent Interactions of Large Molecular Systems Parametrized for All spd-Block Elements (Z = 1–86). J. Chem. Theory Comput. 2017, 13, 1989–2009. [Google Scholar] [CrossRef]
- Khairallah, A.; Bishop, Ö.T.; Moses, V. AMBER force field parameters for the Zn (II) ions of the tunneling-fold enzymes GTP cyclohydrolase I and 6-pyruvoyl tetrahydropterin synthase. J. Biomol. Struct. Dyn. 2020, 28, 1–18. [Google Scholar] [CrossRef]
- Li, X.; Hayik, S.A.; Merz, K.M. QM/MM X-ray refinement of zinc metalloenzymes. J. Inorg. Biochem. 2010, 104, 512–522. [Google Scholar] [CrossRef] [Green Version]
- Harding, M. M The geometry of metal–ligand interactions relevant to proteins. Acta Crystallogr. Sect. D Biol. Crystallogr. 1999, 55, 1432–1443. [Google Scholar] [CrossRef] [PubMed]
- Harding, M.M. Small revisions to predicted distances around metal sites in proteins. Acta Crystallogr D Biol. 2006, 62, 678–682. [Google Scholar] [CrossRef]
- Wei, C.; Lazim, R.; Zhang, D. Importance of polarization effect in the study of metalloproteins: Application of polarized protein specific charge scheme in predicting the reduction potential of azurin. Proteins Struct. Funct. Bioinform. 2014, 82, 2209–2219. [Google Scholar] [CrossRef] [PubMed]
- Tuccinardi, T.; Martinelli, A.; Nuti, E.; Carelli, P.; Balzano, F.; Uccello-Barretta, G.; Murphy, G.; Rossello, A. Amber force field implementation, molecular modelling study, synthesis and MMP-1/MMP-2 inhibition profile of (R)- and (S)-N-hydroxy-2-(N-isopropoxybiphenyl-4-ylsulfonamido)-3-methylbutanamides. Bioorganic Med. Chem. 2006, 14, 4260–4276. [Google Scholar] [CrossRef]
- Smith, D.M.A.; Xiong, Y.; Straatsma, T.P.; Rosso, K.M.; Squier, T.C. Force-Field Development and Molecular Dynamics of [NiFe] Hydrogenase. J. Chem. Theory Comput. 2012, 8, 2103–2114. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Haspel, N.; Moll, M.; Baker, M.L.; Chiu, W.; Kavraki, L.E. Tracing conformational changes in proteins. BMC Struct. Biol. 2010, 10, S1. [Google Scholar] [CrossRef] [Green Version]
- Orellana, L. Large-Scale Conformational Changes and Protein Function: Breaking the in silico Barrier. Front. Mol. Biosci. 2019, 6, 117–136. [Google Scholar] [CrossRef]
- Sheik Amamuddy, O.S.; Glenister, M.; Tastan Bishop, Ö. MDM-TASK-web: A web platform for protein dynamic residue networks and modal analysis. bioRxiv 2021, 2021.01.29.428734, 1–8. [Google Scholar] [CrossRef]
- Bishop, A.; De Beer, T.A.; Joubert, F. Protein homology modelling and its use in South Africa. S. Afr. J. Sci. 2008, 104, 2–6. [Google Scholar]
- Apweiler R, Bairoch A, Wu C: The universal protein resource (UniProt). Nucleic Acids Res. 2007, 36, D190–D195. [CrossRef]
- Söding, J.; Biegert, A.; Lupas, A.N. The HHpred interactive server for protein homology detection and structure prediction. Nucleic Acids Res. 2005, 33, W244–W248. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hatherley, R.; Brown, D.K.; Glenister, M.; Tastan Bishop, Ö. PRIMO: An interactive homology modeling pipeline. PLoS ONE 2016, 11, e0166698. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- ŠAli, A.; Overington, J.P. Derivation of rules for comparative protein modeling from a database of protein structure alignments. Protein Sci. 1994, 3, 1582–1596. [Google Scholar] [CrossRef] [Green Version]
- Ryde, U. Molecular dynamics simulations of alcohol dehydrogenase with a four- or five-coordinate catalytic zinc ion. Proteins Struct. Funct. Bioinform. 1995, 21, 40–56. [Google Scholar] [CrossRef] [Green Version]
- Ryde, U. Combined quantum and molecular mechanics calculations on metalloproteins. Curr. Opin. Chem. Biol. 2003, 7, 136–142. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Rev. A.03; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Bayly, C.I.; Cieplak, P.; Cornell, W.; Kollman, P.A. A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: The RESP model. J. Phys. Chem. 1993, 97, 10269–10280. [Google Scholar] [CrossRef]
- Schafmeister, C.; Ross, W.; Romanovski, V. LEaP; University of California, San Francisco: San Francisco, CA, USA, 1995. [Google Scholar]
- Maier, J.A.; Martinez, C.; Kasavajhala, K.; Wickstrom, L.; Hauser, K.E.; Simmerling, C. ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. [Google Scholar] [CrossRef] [Green Version]
- Da Silva, A.W.S.; Vranken, W.F. ACPYPE—AnteChamber PYthon Parser interfacE. BMC Res. Notes 2012, 5, 367. [Google Scholar] [CrossRef] [Green Version]
- Glättli, A.; Daura, X.; Van Gunsteren, W.F. Derivation of an improved simple point charge model for liquid water: SPC/A and SPC/L. J. Chem. Phys. 2002, 116, 9811–9828. [Google Scholar] [CrossRef]
- Hockney, R.; Goel, S.; Eastwood, J. Quiet high-resolution computer models of a plasma. J. Comput. Phys. 1974, 14, 148–158. [Google Scholar] [CrossRef]
- Petersen, H.G. Accuracy and efficiency of the particle mesh Ewald method. J. Chem. Phys. 1995, 103, 3668–3679. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef] [Green Version]
- Ryckaert, J.-P.; Ciccotti, G.; Berendsen, H.J.C. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef] [Green Version]
- Team R. RStudio. Integrated Development for R. RStudio; RStudio Inc.: Boston, MA, USA, 2015; Volume 42, p. 14. Available online: https://www.rstudio.com (accessed on 20 May 2020.).
- Brown, D.K.; Penkler, D.L.; Amamuddy, O.S.; Ross, C.; Atilgan, A.R.; Atilgan, C.; Bishop, Ö.T. MD-TASK: A software suite for analyzing molecular dynamics trajectories. Bioinformatics 2017, 33, 2768–2771. [Google Scholar] [CrossRef] [Green Version]
- Schrodinger, L. The PyMOL Molecular Graphics System. In BioLuminate; Version 1.8; Schrödinger, LLC.: New York, NY, USA, 2015. [Google Scholar]
- Kluyver, T.; Ragan-Kelley, B.; Pérez, F.; Granger, B.E.; Bussonnier, M.; Frederic, J.; Kelley, K.; Hamrick, J.B.; Grout, J.; Corlay, S. Jupyter Notebooks-A Publishing Format for Reproducible Computational Workflows; IOS Press: Amsterdam, The Netherlands, 2016; pp. 87–90. [Google Scholar]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- McKinney, W. Data Structures for Statistical Computing in Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; pp. 51–56. [Google Scholar]
- Van Der Walt, S.; Colbert, S.C.; Varoquaux, G. The NumPy Array: A Structure for Efficient Numerical Computation. Comput. Sci. Eng. 2011, 13, 22–30. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, H.; Case, D.A.; Rose, A.S. NGLview–interactive molecular graphics for Jupyter notebooks. Bioinformatics 2017, 34, 1241–1242. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sara, J.D.; Kaur, J.; Khodadadi, R.; Rehman, M.; Lobo, R.; Chakrabarti, S.; Herrmann, J.; Lerman, A.; Grothey, A. 5-fluorouracil and cardiotoxicity: A review. Ther. Adv. Med. Oncol. 2018, 10. [Google Scholar] [CrossRef] [Green Version]
- Lonsdale, R.; Harvey, J.N.; Mulholland, A.J. Effects of Dispersion in Density Functional Based Quantum Mechanical/Molecular Mechanical Calculations on Cytochrome P450 Catalyzed Reactions. J. Chem. Theory Comput. 2012, 8, 4637–4645. [Google Scholar] [CrossRef]
- Smith, D.G.A.; Burns, L.A.; Patkowski, K.; Sherrill, C.D. Revised Damping Parameters for the D3 Dispersion Correction to Density Functional Theory. J. Phys. Chem. Lett. 2016, 7, 2197–2203. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef] [PubMed]








| Residue Name | AMBER Protonated Residue Name | Residue Number | pKa Value |
|---|---|---|---|
| Glutamine (Gln) | 1 GLH | 156 | 0.00 |
| Cysteine (Cys) 2 CYM | 79 | 8.37 | |
| 82 | >12.00 | ||
| 87 | >12.00 | ||
| 91 | 8.92 | ||
| 130 | >12.00 | ||
| 136 | >12.00 | ||
| 140 | >5.55 | ||
| 953 | >12.00 | ||
| 956 | 1.93 | ||
| 959 | <0.00 | ||
| 963 | 11.69 | ||
| 986 | >12.00 | ||
| 989 | 8.92 | ||
| 992 | <0.00 | ||
| 996 | 10.50 | ||
| Fe2+4S2−4 Cluster Number | Geometry | Bond Length (Å) | ||||||
|---|---|---|---|---|---|---|---|---|
| Model System | Fe2+4S2−4(S-Cys)3(O-Gln) and ([Fe2+4S2−4(S-Cys)4]) Clusters | |||||||
| Bond | X-ray | 1 QM (2 DFT) | AFTER 3 MD | |||||
| Bond Description | 1H7X | 4 B3LYP (Model 1) | 5 LSDA (Model 2) | Model 1 | Model 2 | |||
| Average Bond Length (Å) | Average Equilibrium Bond Length [req] (Å) | Force Constant [Kr] (kcal·mol−1·Å−2) | Average Equilibrium Bond Length [req] (Å) | Force Constant [Kr] (kcal·mol−1·Å−2) | Bond Length (Å) Mean and6 SD | Bond Length (Å) Mean and 6 SD | ||
| Cluster 1026A | FE-S | 2.54 | 2.24 | 58.63 | 2.22 | 89.23 | 2.24 ± 0.21 | 2.23 ± 0.22 |
| FE-SG (Cys) | 2.35 | 2.37 | 48.72 | 2.33 | 39.77 | 2.37 ± 0.01 | 2.33 ± 0.01 | |
| FE-OE (Gln) | 1.89 | 1.92 | 60.40 | 1.93 | 54.97 | 1.91 ± 0.01 | 1.93 ± 0.04 | |
| Cluster 1027A | FE-S | 2.46 | 2.24 | 57.11 | 2.22 | 89.23 | 2.25 ± 0.15 | 2.23 ± 0.16 |
| FE-SG(Cys) | 2.31 | 2.38 | 40.85 | 2.33 | 39.77 | 2.38 ± 0.05 | 2.33 ± 0.01 | |
| FE-S | 2.58 | 2.24 | 57.11 | 2.22 | 89.23 | 2.25 ± 0.23 | 2.23 ± 0.25 | |
| Cluster 1028B | FE-SG (Cys) | 2.36 | 2.38 | 40.85 | 2.33 | 39.77 | 2.38 ± 0.01 | 2.33 ± 0.02 |
| FE-S | 2.48 | 2.24 | 57.11 | 2.22 | 89.23 | 2.23 ± 0.18 | 2.23 ± 0.18 | |
| FE-SG (Cys) | 2.32 | 2.38 | 40.85 | 2.33 | 39.77 | 2.38 ± 0.04 | 2.33 ± 0.00 | |
| Cluster 1029B | FE-S | 2.54 | 2.24 | 58.63 | 2.22 | 89.23 | 2.24 ± 0.21 | 2.23 ± 0.22 |
| FE-SG (Cys) | 2.35 | 2.37 | 48.72 | 2.33 | 39.77 | 2.37 ± 0.01 | 2.33 ± 0.01 | |
| FE-OE (Gln) | 1.89 | 1.92 | 60.40 | 1.93 | 54.97 | 1.91 ± 0.01 | 1.93 ± 0.04 | |
| Fe2+4S2−4 Cluster Number | Geometry | Angle (°) | ||||||
|---|---|---|---|---|---|---|---|---|
| Model System | Fe2+4S2−4(S-Cys)3(O-Gln) and ([Fe2+4S2−4(S-Cys)4]) Clusters | |||||||
| Angle | X-ray | 1 QM (2 DFT) | AFTER 3 MD | |||||
| Angle Description | 1H7X | 4 B3LYP (Model 1) | 5 LSDA (Model 2) | Model 1 | Model 2 | |||
| Average Angle (°) | Average Equilibrium Angle [Ꝋeq] (°) | Force Constant [KꝊ] (kcal·mol−1·rad−2) | Average Equilibrium Angle[θeq](°) | Force Constant [KꝊ] (kcal·mol−1·rad−2) | Angle (°) Mean and 6 SD | Angle (°) Mean and 6 SD | ||
| Cluster 1026A | FE-S-FE | 67.98 | 67.32 | 52.64 | 66.28 | 26.86 | 62.91 ± 3.59 | 68.10 ± 0.08 |
| S-FE-S | 106.03 | 108.50 | 39.12 | 109.21 | 39.52 | 109.25 ± 2.28 | 106.99 ± 0.68 | |
| Cluster 1027A | FE-S-FE | 68.39 | 67.61 | 49.30 | 66.28 | 26.86 | 64.55 ± 2.72 | 68.24 ± 0.11 |
| S-FE-S | 107.21 | 108.14 | 40.39 | 109.21 | 39.52 | 110.0 ± 1.98 | 108.07 ± 0.61 | |
| Cluster 1028B | FE-S-FE | 68.22 | 67.61 | 49.30 | 66.28 | 26.86 | 66.13 ± 1.48 | 68.30 ± 0.06 |
| S-FE-S | 106.51 | 108.14 | 40.39 | 109.21 | 39.52 | 107.02 ± 0.36 | 106.97 ± 0.33 | |
| Cluster 1029B | FE-S-FE | 67.97 | 67.61 | 49.30 | 66.28 | 26.86 | 65.15 ± 1.99 | 67.48 ± 0.35 |
| S-FE-S | 107.62 | 108.14 | 40.39 | 109.21 | 39.52 | 106.74 ± 0.62 | 107.30 ± 0.23 | |
| Fe2+4S2−4 Cluster Number | Geometry | Angle (°) | ||||||
|---|---|---|---|---|---|---|---|---|
| Model System | Fe2+4S2−4(S-Cys)3(O-Gln) and ([Fe2+4S2−4(S-Cys)4]) Clusters | |||||||
| Bond | X-ray | 1 QM (2 DFT) | AFTER 3 MD | |||||
| Bond Description | 1H7X | 4 B3LYP (Model 1) | 5 GFN1-xTB (Model 2) | Model 1 | Model 2 | |||
| Average Angle (°) | Average Equilibrium Angle (°) | Force constant (kcal·mol−1·rad−2) | Average Equilibrium Angle (°) | Force Constant (kcal·mol−1·rad−2) | Angle (°) Mean and 6 SD | Angle (°) Mean and 6 SD | ||
| Cluster 1026A | C-Gln(OE)-FE | 117.29 | 130.30 | 75.86 | 115.32 | 41.23 | 115.29 ± 1.41 | 114.42 ± 2.02 |
| C-Gln(OE)-H | 104.50 | 122.90 | 80.00 | 118.02 | 44.55 | 113.34 ± 6.25 | 116.93 ± 8.78 | |
| Gln(OE)-FE-S | 107.18 | 109.53 | 48.56 | 113.08 | 40.55 | 111.10 ± 2.77 | 112.09 ± 3.47 | |
| Cluster 1027A | CT-Cys(SG)-FE | 106.87 | 106.27 | 102.22 | 107.39 | 100.90 | 107.56 ± 0.49 | 109.52 ± 1.87 |
| Cys(SG)-CT-H | 108.92 | 109.50 | 50.80 | 104.33 | 23.56 | 101.39 ± 5.32 | 106.06 ± 2.02 | |
| Cys(SG)-FE-S | 110.17 | 110.68 | 53.74 | 113.28 | 36.14 | 108.84 ± 0.94 | 112.60 ± 1.72 | |
| Cluster 1028B | CT-Cys(SG)-FE | 106.72 | 106.27 | 102.22 | 107.39 | 100.90 | 111.35 ± 3.27 | 115.99 ± 6.55 |
| Cys(SG)-CT-H | 107.42 | 109.50 | 50.80 | 104.33 | 23.56 | 106.53 ± 0.63 | 104.94 ± 1.75 | |
| Cys(SG)-FE-S | 110.37 | 110.68 | 53.74 | 113.28 | 36.14 | 110.89 ± 0.37 | 112.35 ± 1.40 | |
| Cluster 1029B | CT-Cys(SG)-FE | 110.70 | 106.27 | 102.22 | 107.39 | 100.90 | 105.99 ± 3.33 | 116.21 ± 3.90 |
| Cys(SG)-CT-H | 110.45 | 109.50 | 50.80 | 104.33 | 36.14 | 105.07 ± 3.80 | 103.38 ± 5.00 | |
| Cys(SG)-FE-S | 110.02 | 110.68 | 53.74 | 113.28 | 36.14 | 110.58 ± 0.40 | 111.20 ± 0.83 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tendwa, M.B.; Chebon-Bore, L.; Lobb, K.; Musyoka, T.M.; Tastan Bishop, Ö. Force Field Parameters for Fe2+4S2−4 Clusters of Dihydropyrimidine Dehydrogenase, the 5-Fluorouracil Cancer Drug Deactivation Protein: A Step towards In Silico Pharmacogenomics Studies. Molecules 2021, 26, 2929. https://doi.org/10.3390/molecules26102929
Tendwa MB, Chebon-Bore L, Lobb K, Musyoka TM, Tastan Bishop Ö. Force Field Parameters for Fe2+4S2−4 Clusters of Dihydropyrimidine Dehydrogenase, the 5-Fluorouracil Cancer Drug Deactivation Protein: A Step towards In Silico Pharmacogenomics Studies. Molecules. 2021; 26(10):2929. https://doi.org/10.3390/molecules26102929
Chicago/Turabian StyleTendwa, Maureen Bilinga, Lorna Chebon-Bore, Kevin Lobb, Thommas Mutemi Musyoka, and Özlem Tastan Bishop. 2021. "Force Field Parameters for Fe2+4S2−4 Clusters of Dihydropyrimidine Dehydrogenase, the 5-Fluorouracil Cancer Drug Deactivation Protein: A Step towards In Silico Pharmacogenomics Studies" Molecules 26, no. 10: 2929. https://doi.org/10.3390/molecules26102929
APA StyleTendwa, M. B., Chebon-Bore, L., Lobb, K., Musyoka, T. M., & Tastan Bishop, Ö. (2021). Force Field Parameters for Fe2+4S2−4 Clusters of Dihydropyrimidine Dehydrogenase, the 5-Fluorouracil Cancer Drug Deactivation Protein: A Step towards In Silico Pharmacogenomics Studies. Molecules, 26(10), 2929. https://doi.org/10.3390/molecules26102929