Equilibrium and Kinetic Study of l- and d-Valine Adsorption in Supramolecular-Templated Chiral Mesoporous Materials
Abstract
:1. Introduction
2. Materials and Methods
2.1. Synthesis of NFM-1
2.2. Synthesis of NGM-1
2.3. Adsorption Equilibrium Measurements
2.4. Freundlich Isotherm
2.5. Langmuir Isotherm
2.6. Circular Dichroism Spectroscopy (CD)
2.7. Low-Angle Powder XRD
2.8. Nitrogen Sorption Isotherms
2.9. Thermogravimetric Analysis
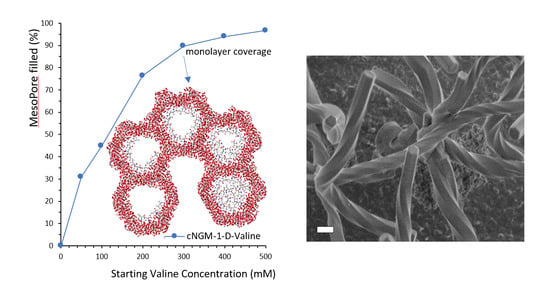
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Cairns-Smith, A.G. Seven Clues to the Origin of Life: A Scientific Detective Story; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Engel, K.-H. Chirality: An Important Phenomenon Regarding Biosynthesis, Perception, and Authenticity of Flavor Compounds. J. Agric. Food Chem. 2020, 68, 10265–10274. [Google Scholar] [CrossRef] [PubMed]
- Morris, R.E.; Bu, X. Induction of chiral porous solids containing only achiral building blocks. Nat. Chem. 2010, 2, 353–361. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Xu, J.; Wang, Y.; Chen, H. Emerging chirality in nanoscience. Chem. Soc. Rev. 2013, 42, 2930–2962. [Google Scholar] [CrossRef] [PubMed]
- Geva, M.; Frolow, F.; Eisenstein, M.; Addadi, L. Antibody recognition of chiral surfaces. Enantiomorphous crystals of leucine-leucine-tyrosine. J. Am. Chem. Soc. 2003, 125, 696–704. [Google Scholar] [CrossRef]
- Somorjai, G.A.; Frei, H.; Park, J.Y. Advancing the frontiers in nanocatalysis, biointerfaces, and renewable energy conversion by innovations of surface techniques. J. Am. Chem. Soc. 2009, 131, 16589–16605. [Google Scholar] [CrossRef] [Green Version]
- Hynes, R.O. The extracellular matrix: Not just pretty fibrils. Science 2009, 326, 1216–1219. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Gan, H.; Sun, T.; Su, B.; Fuchs, H.; Vestweber, D.; Butz, S. Stereochemistry triggered differential cell behaviours on chiral polymer surfaces. Soft Matter 2010, 6, 3851–3855. [Google Scholar] [CrossRef]
- Zhou, F.; Yuan, L.; Li, D.; Huang, H.; Sun, T.; Chen, H. Cell adhesion on chiral surface: The role of protein adsorption. Coll. Surf. Biointerfaces 2012, 90, 97–101. [Google Scholar] [CrossRef]
- El-Gindi, J.; Benson, K.; De Cola, L.; Galla, H.; Kehr, N.S. Cell Adhesion Behavior on Enantiomerically Functionalized Zeolite L Monolayers. Angew. Chem. Int. Ed. 2012, 51, 3716–3720. [Google Scholar] [CrossRef]
- Zhang, M.; Qing, G.; Sun, T. Chiral biointerface materials. Chem. Soc. Rev. 2012, 41, 1972–1984. [Google Scholar] [CrossRef]
- González-Campo, A.; Amabilino, D.B. Biomolecules at Interfaces: Chiral, Naturally. In Topics in Current Chemistry; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2013; Volume 333, pp. 109–156. [Google Scholar]
- Sheldon, R.A. Chirotechnology: Industrial Synthesis of Optically Active Compounds; CRC Press: Boca Raton, FL, USA, 1993. [Google Scholar]
- Xue, M.; Li, B.; Qiu, S.; Chen, B. Emerging functional chiral microporous materials: Synthetic strategies and enantioselective separations. Mater. Today 2016, 19, 503–515. [Google Scholar] [CrossRef]
- Che, S.; Liu, Z.; Ohsuna, T.; Sakamoto, K.; Terasaki, O.; Tatsumi, T. Synthesis and characterization of chiral mesoporous silica. Nat. Cell Biol. 2004, 429, 281–284. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Che, S. Chiral Mesoporous Silica Materials. In Chiral Nanomaterials; Wiley-VCH Verlag GmbH & Co: Weinheim, Germany, 2018; pp. 121–177. [Google Scholar]
- Yokoi, T.; Ogawa, K.; Lu, D.; Kondo, J.N.; Kubota, Y.; Tatsumi, T. Preparation of Chiral Mesoporous Materials with Helicity Perfectly Controlled. Chem. Mater. 2011, 23, 2014–2016. [Google Scholar] [CrossRef]
- Matsukizono, H.; Jin, R.-H. High-Temperature-Resistant Chiral Silica Generated on Chiral Crystalline Templates at Neutral pH and Ambient Conditions. Angew. Chem. Int. Ed. 2012, 51, 5862–5865. [Google Scholar] [CrossRef] [PubMed]
- Ward, T.J.; Baker, B.A. Chiral Separations. Anal. Chem. 2008, 80, 4363–4372. [Google Scholar] [CrossRef] [PubMed]
- Stalcup, A.M. Chiral separations. Annu. Rev. 2010, 3, 341–363. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, L.; Cheng, B.; Zhou, R.; Cao, Z.; Zeng, C.; Li, L. Preparation and evaluation of a novel N-benzyl-phenethylamino-β-cyclodextrin-bonded chiral stationary phase for HPLC. Talanta 2017, 174, 179–191. [Google Scholar] [CrossRef]
- Huang, Y.; Vidal, X.; Garcia-Bennett, A.E. Chiral Resolution using Supramolecular-Templated Mesostructured Materials. Angew. Chem. Int. Ed. 2019, 58, 10859–10862. [Google Scholar] [CrossRef]
- Atluri, R.; Hedin, N.; Garcia-Bennett, A.E. Nonsurfactant Supramolecular Synthesis of Ordered Mesoporous Silica. J. Am. Chem. Soc. 2009, 131, 3189–3191. [Google Scholar] [CrossRef]
- Atluri, R.; Iqbal, M.N.; Bacsik, Z.; Hedin, N.; Villaescusa, L.A.; Garcia-Bennett, A.E. Self-Assembly Mechanism of Folate-Templated Mesoporous Silica. Langmuir 2013, 29, 12003–12012. [Google Scholar] [CrossRef]
- Bueno-Alejo, C.J.; Villaescusa, L.A.; Garcia-Bennett, A.E. Supramolecular transcription of guanosine monophosphate into mesostructured silica. Angew. Chem. Int. Ed. Engl 2014, 53, 12106–12110. [Google Scholar] [CrossRef] [PubMed]
- Care, A.; Bergquist, P.L.; Sunna, A. Solid-binding peptides: Smart tools for nanobiotechnology. Trends Biotechnol. 2015, 33, 259–268. [Google Scholar] [CrossRef] [PubMed]
- Freundlich, H. Über die adsorption in lösungen. Z. Phys. Chem. 1907, 57, 385–470. [Google Scholar] [CrossRef]
- Ho, Y.S.; Porter, J.F.; McKay, G. Equilibrium Isotherm Studies for the Sorption of Divalent Metal Ions onto Peat: Copper, Nickel and Lead Single Component Systems. Water Air Soil Pollut. 2002, 141, 1–33. [Google Scholar] [CrossRef]
- Langmuir, I. The constitution and fundamental properties of solids and liquids. Part I: Solids. J. Am. Chem. Soc. 1916, 38, 2221–2295. [Google Scholar] [CrossRef] [Green Version]
- Umpleby, R.J.; Baxter, S.C.; Chen, Y.; Shah, R.N.; Shimizu, K.D. Characterization of Molecularly Imprinted Polymers with the Langmuir-Freundlich Isotherm. Anal. Chem. 2001, 73, 4584–4591. [Google Scholar] [CrossRef]
- Langmuir, I. The adsorption of gases on plane surfaces of glass, mica and platinum. J. Am. Chem. Soc. 1918, 40, 1361–1403. [Google Scholar] [CrossRef] [Green Version]
- Hall, K.R.; Eagleton, L.C.; Acrivos, A.; Vermeulen, T. Pore- and Solid-Diffusion Kinetics in Fixed-Bed Adsorption under Constant-Pattern Conditions. Ind. Eng. Chem. Fundam. 1966, 5, 212–223. [Google Scholar] [CrossRef]
- McKay, G. Adsorption of dyestuffs from aqueous solutions with activated carbon I: Equilibrium and batch contact-time studies. J. Chem. Tech. Biotech. 1982, 32, 759–772. [Google Scholar] [CrossRef]
- Weber, T.W.; Chakravorti, R.K. Pore and solid diffusion models for fixed-bed adsorbers. AIChE J. 1974, 20, 228–238. [Google Scholar] [CrossRef]
- Atluri, R.; Hedin, N.; Garcia-Bennett, A.E. Hydrothermal Phase Transformation of Bicontinuous Cubic Mesoporous Material AMS-6. Chem. Mater. 2008, 20, 3857–3866. [Google Scholar] [CrossRef]
- Lund, K.; Muroyama, N.; Terasaki, O. Accidental extinction in powder XRD intensity of porous crystals: Mesoporous carbon crystal CMK-5 and layered zeolite-nanosheets. Microporous Mesoporous Mater. 2010, 128, 71–77. [Google Scholar] [CrossRef]
- Torii, K.; Iitaka, Y. The crystal structure of L-valine. Acta Cryst. 1970, 26, 1317–1326. [Google Scholar] [CrossRef] [PubMed]
- Gao, Q.; Xu, W.; Xu, Y.; Wu, D.; Sun, Y.; Deng, F.; Shen, W. Amino Acid Adsorption on Mesoporous Materials: Influence of Types of Amino Acids, Modification of Mesoporous Materials, and Solution Conditions. J. Phys. Chem. B 2008, 112, 2261–2267. [Google Scholar] [CrossRef]
- Goscianska, J.; Olejnik, A.; Pietrzak, R. Comparison of ordered mesoporous materials sorption properties towards amino acids. Adsorption 2013, 19, 581–588. [Google Scholar] [CrossRef] [Green Version]
- Wei, L.; Shi, D.; Zhou, Z.; Ye, P.; Wang, J.; Zhao, J.; Liu, L.; Chen, C.; Yang, Z. Functionalized self-assembled monolayers on mesoporous silica nanoparticles with high surface coverage. Nanoscale Res. Lett. 2012, 7, 334. [Google Scholar] [CrossRef] [Green Version]
- Ayawei, N.; Ebelegi, A.N.; Wankasi, D. Modelling and Interpretation of Adsorption Isotherms. J. Chem. 2017, 2017, 1–11. [Google Scholar] [CrossRef]







| cNGM-1 (d-Valine) | cNFM-1 (l-Valine) | |||
|---|---|---|---|---|
| Parameters | R2 | Parameters | R2 | |
| Freundlich | KF = 8.97 L/g nF = 2.96 | 0.99 | KF = 3.47 L/g nF = 2.44 | 0.95 |
| Langmuir | qmax = 0.36 g/g KL = 0.057 L/g aL = 2 × 10−4 L/mg RL = 0.09–0.5 | 0.99 | qmax = 0.26 g/g KL = 0.055 L/g aL = 2 × 10−4 L/mg RL = 0.20–0.73 | 0.99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Garcia-Bennett, A.E. Equilibrium and Kinetic Study of l- and d-Valine Adsorption in Supramolecular-Templated Chiral Mesoporous Materials. Molecules 2021, 26, 338. https://doi.org/10.3390/molecules26020338
Huang Y, Garcia-Bennett AE. Equilibrium and Kinetic Study of l- and d-Valine Adsorption in Supramolecular-Templated Chiral Mesoporous Materials. Molecules. 2021; 26(2):338. https://doi.org/10.3390/molecules26020338
Chicago/Turabian StyleHuang, Yanan, and Alfonso E. Garcia-Bennett. 2021. "Equilibrium and Kinetic Study of l- and d-Valine Adsorption in Supramolecular-Templated Chiral Mesoporous Materials" Molecules 26, no. 2: 338. https://doi.org/10.3390/molecules26020338
APA StyleHuang, Y., & Garcia-Bennett, A. E. (2021). Equilibrium and Kinetic Study of l- and d-Valine Adsorption in Supramolecular-Templated Chiral Mesoporous Materials. Molecules, 26(2), 338. https://doi.org/10.3390/molecules26020338