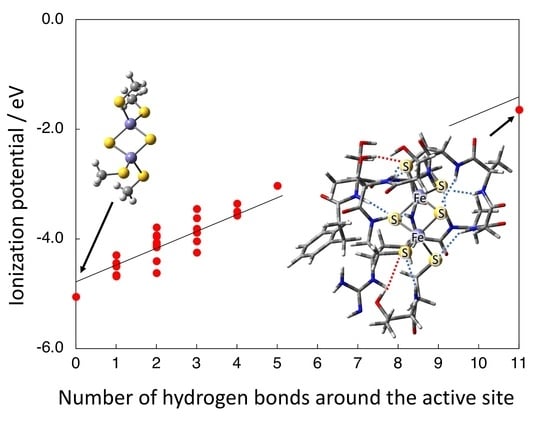
Theoretical Study on Redox Potential Control of Iron-Sulfur Cluster by Hydrogen Bonds: A Possibility of Redox Potential Programming
Abstract
:1. Introduction
2. Computational Models
2.1. Calculated Model Structures
2.2. Calculation of the Vertical Ionization Potential of the Reduced State (IP(red))
3. Results and Discussion
3.1. Electronic Structures of the Oxidized and Reduced States
3.2. Calculated Vertical Ionization Potential (IP(red)) of 1H and 1N
3.3. Effect of [N-H…S] Hydrogen Bond from the Peptide on IP(red)
3.4. Effect of [O-H…S] Hydrogen Bond from the Side Chains on IP(red)
3.5. Possible Mechanism for the Effect of Hydrogen Bond on IP(red)
4. Materials and Methods
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Messerschmidt, A.; Huber, R.; Poulos, T.; Wieghardt, K. (Eds.) Handbook of Metalloproteins; John Wiley & Sons, Ltd.: Chichester, UK, 2001. [Google Scholar]
- Liu, J.; Chakraborty, S.; Hosseinzadeh, P.; Yu, Y.; Tian, S.; Petrik, I.; Bhagi, A.; Lu, Y. Metalloproteins Containing Cytochrome, Iron–Sulfur, or Copper Redox Centers. Chem. Rev. 2014, 114, 4366–4469. [Google Scholar]
- Lippard, S.J.; Berg, J.M. Principles of Bioinorganic Chemistry; University Science Books: Sausalito, CA, USA, 1994; Chapter 12. [Google Scholar]
- Fee, J.A.; Castagenetto, J.M.; Case, D.A.; Noodleman, L.; Stout, C.D.; Torres, R.A. The circumsphere as a tool to assess distortion in [4Fe–4S] atom clusters. J. Biol. Inorg. Chem. 2003, 8, 519–526. [Google Scholar] [CrossRef]
- Li, J.; Nelson, M.R.; Peng, C.Y.; Bashford, D.; Noodleman, L. Incorporating Protein Environments in Density Functional Theory: A Self-Consistent Reaction Field Calculation of Redox Potentials of [2Fe2S] Clusters in Ferredoxin and Phthalate Dioxygenase Reductase. J. Phys. Chem. A 1998, 102, 6311–6324. [Google Scholar] [CrossRef]
- Liu, L.; Nogi, T.; Kobayashi, M.; Nozawa, T.; Miki, K. Ultrahigh-resolution structure of high-potential iron-sulfur protein from Thermochromatium tepidum. Acta. Cryst. 2002, 58, 1085–1091. [Google Scholar]
- Torres, R.A.; Lovell, T.; Noodleman, L.; Case, D.A. Density Functional and Reduction Potential Calculations of Fe4S4 Clusters. J. Am. Chem. Soc. 2003, 125, 1923–1936. [Google Scholar] [CrossRef] [PubMed]
- Mouesca, J.M.; Chen, J.L.; Noodleman, L.; Bashford, D.; Case, D. Density Functional/Poisson-Boltzmann Calculations of Redox Potentials for Iron-Sulfur Clusters. J. Am. Chem. Soc. 1994, 116, 11898–11914. [Google Scholar] [CrossRef]
- Glaser, T.; Bertini, I.; Moura, J.J.G.; Hedman, B.; Hodgson, K.O.; Solomon, E.I. Protein Effects on the Electronic Structure of the [Fe4S4]2+ Cluster in Ferredoxin and HiPIP. J. Am. Chem. Soc. 2001, 123, 4859–4860. [Google Scholar] [CrossRef] [PubMed]
- Dey, A.; Jenny, F.E., Jr.; Adams, M.W.W.; Babini, E.; Takahashi, Y.; Fukuyama, K.; Hodgson, K.O.; Hedman, B.; Solomon, E.I. Solvent Tuning of Electrochemical Potentials in the Active Sites of HiPIP Versus Ferredoxin. Science 2007, 318, 1464–1468. [Google Scholar] [CrossRef] [PubMed]
- Kerfeld, C.A.; Salmeen, A.E.; Yeates, T.O. Crystal structure and possible dimerization of the high-potential iron-sulfur protein from Chromatium purpuratum. Biochemistry 1998, 37, 13911–13917. [Google Scholar] [CrossRef]
- Fukuyama, K.; Okada, T.; Kakuda, Y.; Takahashi, Y. Atomic resolution structures of oxidized [4Fe-4S] ferredoxin from Bacillus thermoproteolyticus in two crystal forms: Systematic distortion of [4Fe-4S] cluster in the protein. J. Mol. Biol. 2002, 315, 1155–1166. [Google Scholar] [CrossRef]
- Gámiz-Hernández, A.P.; Galstyan, A.S.; Knapp, E.-W. Understanding Rubredoxin Redox Potentials: Role of H-Bonds on Model Complexes. J. Chem. Theory Comput. 2009, 5, 2898–2908. [Google Scholar] [CrossRef] [PubMed]
- Szilagyi, R.K.; Winslow, M.A. On the accuracy of density functional theory for iron-sulfur clusters. J. Comput. Chem. 2006, 27, 1385–1397. [Google Scholar] [CrossRef] [PubMed]
- Kurniawan, I.; Kawaguchi, K.; Shoji, M.; Matsui, T.; Shigeta, Y.; Nagao, H. A Theoretical Study on Redox Potential and pKa of [2Fe-2S] Cluster Model from Iron-Sulfur Proteins. Bull. Chem. Soc. Jpn. 2018, 91, 1451–1456. [Google Scholar] [CrossRef]
- Matsui, T.; Kitagawa, Y.; Shigeta, Y.; Okumura, M. A Density Functional Theory Based Protocol to Compute the Redox Potential of Transition Metal Complex with the Correction of Pseudo-Counterion: General Theory and Applications. J. Chem. Theory Comput. 2013, 9, 2974–2980. [Google Scholar] [CrossRef]
- Shoji, M.; Koizumi, K.; Taniguchi, T.; Kitagawa, Y.; Kawakami, T.; Yamanaka, S.; Okumura, M.; Yamaguchi, K. Theory of chemical bonds in metalloenzymes III: Full geometry optimization and vibration analysis of ferredoxin-type [2Fe-2S] cluster. Int. J. Quant. Chem. 2007, 107, 116–133. [Google Scholar] [CrossRef]
- Shoji, M.; Koizumi, K.; Kitagawa, Y.; Yamanaka, S.; Okumura, M.; Yamaguchi, K. Theory of chemical bonds in metalloenzymes IV: Hybrid-DFT study of Rieske-type [2Fe-2S] clusters. Int. J. Quant. Chem. 2007, 107, 609–627. [Google Scholar] [CrossRef]
- Kitagawa, Y.; Shoji, M.; Nakanishi, Y.; Koizumi, K.; Kawakami, T.; Okumura, M.; Yamaguchi, K. Theoretical studies on effects of hydrogen bonds attaching to cysteine ligands on 4Fe-4S clusters. Int. J. Quant. Chem. 2008, 108, 2881–2887. [Google Scholar] [CrossRef]
- Noodleman, L.; Case, D. Density-Functional Theory of Spin Polarization and Spin Coupling in Iron-Sulfur Clusters. Adv. Inorg. Chem. 1992, 38, 423–470. [Google Scholar]
- Ohki, Y.; Uchida, K.; Tada, M.; Cramer, R.E.; Ogura, T.; Ohta, T. N2 activation on a molybdenum-titanium-sulfur cluster. Nat. Comm. 2018, 9, 3200. [Google Scholar] [CrossRef] [PubMed]
- Holm, R.H.; Lo, W. Structural Conversions of Synthetic and Protein-Bound Iron−Sulfur Clusters. Chem. Rev. 2016, 116, 13685–13713. [Google Scholar] [CrossRef]
- Ohta, S.; Ohki, Y. Impact of ligands and media on the structure and properties of biological and biomimetic iron-sulfur clusters. Coord. Chem. Rev. 2017, 338, 207–225. [Google Scholar] [CrossRef]
- Hanke, G.T.; Kimata-Ariga, Y.; Taniguchi, I.; Hase, T. A Post Genomic Characterization of Arabidopsis Ferredoxins. Plant Physiol. 2004, 134, 255–264. [Google Scholar] [CrossRef] [Green Version]
- Ewen, K.M.; Ringle, M.; Bernhardt, R. Adrenodoxin—A versatile ferredoxin. IUBMB Life 2012, 64, 506–512. [Google Scholar] [CrossRef]
- Morales, R.; Charon, M.-H.; Hudry-Clergeon, G.; Pétillot, Y.; Norager, S.; Medina, M.; Frey, M. Refined X-ray Structures of the Oxidized, at 1.3 Å, and Reduced, at 1.17 Å, [2Fe−2S] Ferredoxin from the Cyanobacterium Anabaena PCC7119 Show Redox-Linked Conformational Changes. Biochemistry 1999, 38, 15764–15773. [Google Scholar] [CrossRef]
- Mavros, M.G.; Tsuchimochi, T.; Kowalczyk, T.; McIsaac, A.; Wang, L.-P.; Voorhis, T.V. What Can Density Functional Theory Tell Us about Artificial Catalytic Water Splitting? Inorg. Chem. 2014, 53, 6386–6397. [Google Scholar] [CrossRef] [PubMed]
- Cerón-Carrasco, J.P.; Jacquemin, D.; Laurent, A.D. First computational step towards the understanding of the antioxidant activity of the Phycocyanobilin:Ferredoxin Oxidoreductase in complex with biliverdin IXα. Comput. Theoret. Chem. 2016, 1077, 58–64. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision C.01; Gaussian: Wallingford, CT, USA, 2009. [Google Scholar]
- Baik, M.-H.; Frisner, R.A. Computing redox potentials in solution: Density functional theory as a tool for rational design of redox agents. J. Phys. Chem. A 2002, 106, 7407–7412. [Google Scholar] [CrossRef]





| Type of Hydrogen Bond | Proton Donor (D) | Sulfur (S) | D-S Distance/Å | rH–S/Å | ∠D-H⋯S/deg | Group |
|---|---|---|---|---|---|---|
| [N-H…S] | Cys41 | 46Sγ | 3.94 | 2.93 | 172.0 | Group 1 |
| Ala43 | 41Sγ | 3.28 | 2.29 | 154.1 | ||
| Ala45 | 41Sγ | 3.39 | 2.46 | 146.6 | ||
| Thr48 | 46Sγ | 3.40 | 2.40 | 165.6 | ||
| Ser40 | S1 | 3.28 | 2.26 | 176.4 | Group 2 | |
| Arg42 | S1 | 3.29 | 2.32 | 160.7 | ||
| Cys46 | S2 | 3.35 | 2.49 | 142.4 | ||
| Gly44 | 79Sγ | 3.54 | 2.63 | 148.8 | Group 3 | |
| Cys79 | 49Sγ | 3.55 | 2.56 | 163.9 | ||
| [O-H…S] a) | Thr48 | 46Sγ | 3.49 | 2.59 | 153.8 | Group 1 |
| Thr78 b) | 49Sγ | 3.95 | 3.16 | 139.0 | Group 3 |
| States | Atoms b) | |||||||
|---|---|---|---|---|---|---|---|---|
| Fe1 | Fe2 | S1 | S2 | 41Sγ | 46Sγ | 49Sγ | 79Sγ | |
| ox | −3.82 (−3.75) | 3.75 (3.72) | −0.06 (0.02) | −0.07 (0.01) | −0.16 (−0.22) | −0.19 (−0.25) | 0.26 (0.23) | 0.28 (0.24) |
| red | −3.68 (−3.52) | 3.79 (3.72) | 0.17 (0.28) | 0.29 (0.31) | −0.03 (−0.07) | −0.03 (−0.10) | 0.22 (0.19) | 0.21 (0.18) |
| Model | Total Energy/Hartree | IP(red)/eV | |
|---|---|---|---|
| ox State | red State | ||
| 1N | −5076.2451 | −5076.0590 | −5.06 |
| 1H | −8648.4040 | −8648.3435 | −1.65 |
| 1H’a) | −7440.6109 | −7440.5334 | −2.11 |
| Number of Hydrogen Bonds | Donor | Group | Total Energy/Hartree | IP(red)/eV | |
|---|---|---|---|---|---|
| ox State | red State | ||||
| 1 | Cys41 | Group 1 | −5323.5846 | −5323.4139 | −4.65 |
| Ala43 | −5324.7894 | −5324.6185 | −4.65 | ||
| Ala45 | −5324.7805 | −5324.6077 | −4.70 | ||
| Thr48 | −5324.7866 | −5324.6139 | −4.70 | ||
| Ser40 | Group 2 | −5324.7890 | −5324.6200 | −4.60 | |
| Arg42 | −5323.5841 | −5323.4138 | −4.63 | ||
| Cys46 | −5323.5845 | −5323.4120 | −4.69 | ||
| Gly44 | Group 3 | −5324.7886 | −5324.6168 | −4.68 | |
| Cys79 | −5323.5894 | −5323.4159 | −4.72 | ||
| 2 | Cys41, Ala43 | Group 1 | −5572.1223 | −5571.9652 | −4.28 |
| Cys41, Ala45 | −5572.1153 | −5571.9569 | −4.31 | ||
| Cys41, Thr48 | −5572.1213 | −5571.9633 | −4.30 | ||
| Ala43, Ala45 | −5573.3182 | −5573.1597 | −4.31 | ||
| Ala43, Thr48 | −5573.3266 | −5573.1689 | −4.29 | ||
| Ala45, Thr48 | −5573.3180 | −5573.1584 | −4.34 | ||
| Ser40, Arg42 | Group 2 | −5572.1189 | −5571.9645 | −4.20 | |
| Ser40, Cys46 | −5572.1239 | −5571.9679 | −4.25 | ||
| Ser40, Cys46 | −5570.9203 | −5570.7632 | −4.27 | ||
| Gly44, Cys79 | Group 3 | −5572.1282 | −5571.9683 | −4.35 | |
| 3 | Cys41, Ala43, Ala45 | Group 1 | −5820.6497 | −5820.5042 | −3.96 |
| Cys41, Ala43, Thr48 | −5820.6581 | −5820.5136 | −3.93 | ||
| Cys41, Ala45, Thr48 | −5820.6508 | −5820.5048 | −3.97 | ||
| Ala43, Ala45, Thr48 | −5821.8544 | −5821.7086 | −3.97 | ||
| Ser40, Arg42, Cys46 | Group 2 | −5819.4560 | −5819.3141 | −3.86 | |
| 4 | Cys41, Ala43, Ala45, Thr48 | Group 1 | −6069.1848 | −6069.0517 | −3.62 |
| 9 | 1H’ | −7440.6109 | −7440.5334 | −2.11 | |
| 0 | 1N | −5076.2451 | −5076.0590 | −5.06 | |
| Number of Hydrogen Bonds | Donor | Group | Total Energy/Hartree | IP(red)/eV | |
|---|---|---|---|---|---|
| ox State | red State | ||||
| 1 | Cys41 | Group 1 | −5438.1031 | −5437.9377 | −4.50 |
| 1 | Ala43 | −5686.1898 | −5686.0264 | −4.45 | |
| 1 | Ala45 | −5364.0965 | −5363.9243 | −4.68 | |
| 2 | Thr48 a) | −5593.1554 | −5592.9936 | −4.40 | |
| 1 | Ser40 | Group 2 | −5709.6638 | −5709.5060 | −4.29 |
| 1 | Arg42 | −5645.6609 | −5645.4976 | −4.44 | |
| 1 | Cys46 | −5362.8987 | −5362.7272 | −4.67 | |
| 1 | Gly44 | Group 3 | −5364.1027 | −5363.9314 | −4.66 |
| 2 | [Cys79 + Thr78] b) | −5477.4287 | −5477.2587 | −4.62 | |
| 2 | Cys41, Ala43 | Group 1 | −6048.0384 | −6047.8936 | −3.94 |
| 2 | Cys41, Ala45 | −5725.9494 | −5725.7968 | −4.15 | |
| 3 | Cys41, Thr48 a) | −5955.0059 | −5954.8629 | −3.89 | |
| 2 | Ala43, Ala45 | −5974.0329 | −5973.8819 | −4.11 | |
| 3 | Ala43, Thr48 a) | −6203.0941 | −6202.9540 | −3.81 | |
| 3 | Ala45, Thr48 a) | −5881.0021 | −5880.8534 | −4.05 | |
| 2 | Ser40, Arg42 | Group 2 | −6279.0694 | −6278.9301 | −3.79 |
| 2 | Ser40, Cys46 | −5996.3130 | −5996.1675 | −3.96 | |
| 2 | Ser40, Cys46 | −5932.3110 | −5932.1615 | −4.07 | |
| 3 | Gly44, [Cys79 + Thr78] b) | Group 3 | −5765.2810 | −5765.1250 | −4.24 |
| 3 | Cys41, Ala43, Ala45 | Group 1 | −6335.8810 | −6335.7479 | −3.62 |
| 4 | Cys41, Ala43, Thr48 a) | −6564.9397 | −6564.8166 | −3.35 | |
| 4 | Cys41, Ala45, Thr48 a) | −6242.8505 | −6242.7194 | −3.57 | |
| 4 | Ala43, Ala45, Thr48 a) | −6490.9357 | −6490.8073 | −3.50 | |
| 3 | Ser40, Arg42, Cys46 | Group 2 | −6565.7175 | −6565.5907 | −3.45 |
| 5 | Cys41, Ala43, Ala45, Thr48 a) | Group 1 | −6852.7799 | −6852.6688 | −3.03 |
| 11 | 1H | −8648.4040 [−8648.6202] | −8648.3435 [−8648.7427] | −1.65 [3.32] | |
| 0 | 1N | −5076.2451 [−5076.5020] | −5076.0590 [−5076.6082] | −5.06 [2.89] | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Era, I.; Kitagawa, Y.; Yasuda, N.; Kamimura, T.; Amamizu, N.; Sato, H.; Cho, K.; Okumura, M.; Nakano, M. Theoretical Study on Redox Potential Control of Iron-Sulfur Cluster by Hydrogen Bonds: A Possibility of Redox Potential Programming. Molecules 2021, 26, 6129. https://doi.org/10.3390/molecules26206129
Era I, Kitagawa Y, Yasuda N, Kamimura T, Amamizu N, Sato H, Cho K, Okumura M, Nakano M. Theoretical Study on Redox Potential Control of Iron-Sulfur Cluster by Hydrogen Bonds: A Possibility of Redox Potential Programming. Molecules. 2021; 26(20):6129. https://doi.org/10.3390/molecules26206129
Chicago/Turabian StyleEra, Iori, Yasutaka Kitagawa, Natsumi Yasuda, Taigo Kamimura, Naoka Amamizu, Hiromasa Sato, Keigo Cho, Mitsutaka Okumura, and Masayoshi Nakano. 2021. "Theoretical Study on Redox Potential Control of Iron-Sulfur Cluster by Hydrogen Bonds: A Possibility of Redox Potential Programming" Molecules 26, no. 20: 6129. https://doi.org/10.3390/molecules26206129
APA StyleEra, I., Kitagawa, Y., Yasuda, N., Kamimura, T., Amamizu, N., Sato, H., Cho, K., Okumura, M., & Nakano, M. (2021). Theoretical Study on Redox Potential Control of Iron-Sulfur Cluster by Hydrogen Bonds: A Possibility of Redox Potential Programming. Molecules, 26(20), 6129. https://doi.org/10.3390/molecules26206129