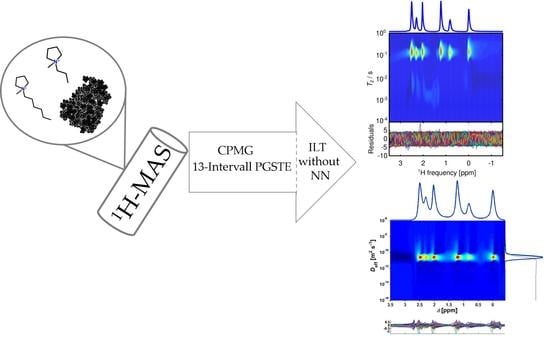
MAS-NMR of [Pyr13][Tf2N] and [Pyr16][Tf2N] Ionic Liquids Confined to Carbon Black: Insights and Pitfalls
Abstract
:1. Introduction
2. Results and Discussion
2.1. IL Loading Dependence of 1H NMR Spectra
2.2. 1H-T2,app Time Distributions
2.3. Diffusion Measurements
2.4. Technical Aspects
2.5. Influence of Centrifugal Forces
2.6. Influence of Sample Preparation and NMR Parameters on MAS Measurements
3. Materials and Methods
3.1. Sample Preparation and Characterization
3.2. 1H-NMR Measurements
3.3. Data Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Li, M.; Wang, C.; Chen, Z.; Xu, K.; Lu, J. New Concepts in Electrolytes. Chem. Rev. 2020, 120, 6783–6819. [Google Scholar] [CrossRef] [PubMed]
- Gouverneur, M.; Kopp, J.; van Wullen, L.; Schonhoff, M. Direct determination of ionic transference numbers in ionic liquids by electrophoretic NMR. Phys. Chem. Chem. Phys. 2015, 17, 30680–30686. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karger, J.; Ruthven, D.M. Diffusion in nanoporous materials: Fundamental principles, insights and challenges. New J. Chem. 2016, 40, 4027–4048. [Google Scholar] [CrossRef] [Green Version]
- Hardy, E.H. NMR Methods for the Investigation of Structure and Transport; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
- Abragam, A. The Principles of Nuclear Magnetism; Oxford University Press: Clarendon, TX, USA, 1961. [Google Scholar]
- Keeler, J. Understanding NMR Spectroscopy; Wiley: Chichester, UK, 2005. [Google Scholar]
- Markley, J.L.; Opella, S.J. Biological NMR Spectroscopy; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Günther, H. NMR Spectroscopy: Basic Principles, Concepts and Applications in Chemistry; Wiley: Weinheim, Germany, 2013. [Google Scholar]
- Ernst, R.R.; Bodenhausen, G.; Wokaun, A. Principles of Nuclear Magnetic Resonance in One and Two Dimensions; Clerendon Press: Oxford, UK, 1987. [Google Scholar]
- Jeener, J.; Meier, B.H.; Bachmann, P.; Ernst, R.R. Investigation of exchange processes by two-dimensional NMR spectroscopy. J. Chem. Phys. 1979, 71, 4546–4553. [Google Scholar] [CrossRef]
- Callaghan, P.T.; Furó, I. Diffusion-diffusion correlation and exchange as a signature for local order and dynamics. J. Chem. Phys. 2004, 120, 4032–4038. [Google Scholar] [CrossRef]
- Stallmach, F.; Galvosas, P. Spin echo NMR diffusion studies. Annual Reports on NMR Spectroscopy; Webb, G.A., Ed.; Academic Press: London, UK, 2007; Volume 61, pp. 51–131. [Google Scholar]
- Stejskal, E.O.; Tanner, J.E. Spin Diffusion Measurements: Spin Echoes in the Presence of a Time-Dependent Field Gradient. J. Chem. Phys. 1965, 42, 288–292. [Google Scholar] [CrossRef] [Green Version]
- Andrew, E.R.; Bradbury, A.; Eades, R.G. Removal of Dipolar Broadening of Nuclear Magnetic Resonance Spectra of Solids by Specimen Rotation. Nature 1959, 183, 1802–1803. [Google Scholar] [CrossRef]
- Reif, B.; Ashbrook, S.E.; Emsley, L.; Hong, M. Solid-state NMR spectroscopy. Nat. Rev. Methods Primers 2021, 1, 2. [Google Scholar] [CrossRef]
- Pampel, A.; Michel, D.; Reszka, R. Pulsed field gradient MAS-NMR studies of the mobility of carboplatin in cubic liquid-crystalline phases. Chem. Phys. Lett. 2002, 357, 131–136. [Google Scholar] [CrossRef]
- Gratz, M.; Hertel, S.; Wehring, M.; Stallmach, F.; Galvosas, P. Mixture diffusion of adsorbed organic compounds in metal-organic frameworks as studied by magic-angle spinning pulsed-field gradient nuclear magnetic resonance. New J. Phys. 2011, 13, 45016. [Google Scholar] [CrossRef] [Green Version]
- Taylor, A.J.; Granwehr, J.; Lesbats, C.; Krupa, J.L.; Six, J.S.; Pavlovskaya, G.E.; Thomas, N.R.; Auer, D.P.; Meersmann, T.; Faas, H.M. Probe-Specific Procedure to Estimate Sensitivity and Detection Limits for 19F Magnetic Resonance Imaging. PLoS ONE 2016, 11, e163704. [Google Scholar] [CrossRef] [Green Version]
- Asano, A.; Hori, S.; Kitamura, M.; Nakazawa, C.T.; Kurotsu, T. Influence of magic angle spinning on T1H of SBR studied by solid state 1H NMR. Polym. J. 2012, 44, 706–712. [Google Scholar] [CrossRef] [Green Version]
- Patrick, J.W. Porosity in Carbons: Characterization and Applications; Edward Arnold: London, UK, 1995. [Google Scholar]
- Schröder, A.; Klüppel, M.; Schuster, R.H.; Heidberg, J. Surface energy distribution of carbon black measured by static gas adsorption. Carbon 2002, 40, 207–210. [Google Scholar] [CrossRef]
- Sebok, E.B.; Taylor, R.L. Carbon Blacks. In Encyclopedia of Materials: Science and Technology; Buschow, K.H.J., Cahn, R.W., Flemings, M.C., Ilschner, B., Kramer, E.J., Mahajan, S., Veyssière, P., Eds.; Elsevier: Oxford, UK, 2001; pp. 902–906. [Google Scholar]
- Dicks, A.L. The role of carbon in fuel cells. J. Power Sources 2006, 156, 128–141. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, H.; Ji, S.; Goh, J.; Feng, H.; Wang, R. Highly active Vulcan carbon composite for oxygen reduction reaction in alkaline medium. Electrochim. Acta 2014, 133, 391–398. [Google Scholar] [CrossRef]
- Pan, Y.; Xu, K.; Wu, C. Recent progress in supercapacitors based on the advanced carbon electrodes. Nanotechnol. Rev. 2019, 8, 299–314. [Google Scholar] [CrossRef]
- Liu, R.; Wang, Y.; Li, B.; Liu, B.; Ma, H.; Li, D.; Dong, L.; Li, F.; Chen, X.; Yin, X. VXC-72R/ZrO2/GCE-Based Electrochemical Sensor for the High-Sensitivity Detection of Methyl Parathion. Materials 2019, 12, 3637. [Google Scholar] [CrossRef] [Green Version]
- El Khatib, K.; Hameed, R. Development of Cu2O/Carbon Vulcan XC-72 as non-enzymatic sensor for glucose determination. Biosens. Bioelectron. 2011, 26, 3542–3548. [Google Scholar] [CrossRef]
- Khodabakhshi, S.; Fulvio, P.F.; Andreoli, E. Carbon black reborn: Structure and chemistry for renewable energy harnessing. Carbon 2020, 162, 604–649. [Google Scholar] [CrossRef] [Green Version]
- Wissler, M. Graphite and carbon powders for electrochemical applications. J. Power Sources 2006, 156, 142–150. [Google Scholar] [CrossRef]
- Manickam, M.; Takata, M. Electrochemical and X-ray photoelectron spectroscopy studies of carbon black as an additive in Li batteries. J. Power Sources 2002, 112, 116–120. [Google Scholar] [CrossRef]
- Fransson, L.; Eriksson, T.; Edström, K.; Gustafsson, T.; Thomas, J.O. Influence of carbon black and binder on Li-ion batteries. J. Power Sources 2001, 101, 1–9. [Google Scholar] [CrossRef]
- Kaisheva, A.; Iliev, I. Application of Carbon-Based Materials in Metal-Air Batteries: Research, Development, Commercialization. In New Carbon Based Materials for Electrochemical Energy Storage Systems: Batteries, Supercapacitors and Fuel Cells; Springer: Dordrecht, Netherland, 2006; pp. 117–136. [Google Scholar]
- Hayes, R.; Warr, G.G.; Atkin, R. Structure and Nanostructure in Ionic Liquids. Chem. Rev. 2015, 115, 6357–6426. [Google Scholar] [CrossRef] [Green Version]
- Tiago, G.; Matias, I.; Ribeiro, A.; Martins, L. Application of Ionic Liquids in Electrochemistry-Recent Advances. Molecules 2020, 25, 5812. [Google Scholar] [CrossRef]
- Torriero, A. Electrochemistry in Ionic Liquids: Volume 1: Fundamentals; Springer: Cham, Switzerland, 2015; pp. 1–351. [Google Scholar]
- Torriero, A. Electrochemistry in Ionic Liquids: Volume 2: Applications; Springer: Cham, Switzerland, 2015; pp. 1–623. [Google Scholar]
- MacFarlane, D.; Kar, M.; Pringle, J.M. Fundamentals of Ionic Liquids: From Chemistry to Applications; Wiley: Weinheim, Germany, 2017. [Google Scholar]
- Smith, A.; Lovelock, K.; Gosvami, N.; Licence, P.; Dolan, A.; Welton, T.; Perkin, S. Monolayer to Bilayer Structural Transition in Confined Pyrrolidinium-Based Ionic Liquids. J. Phys. Chem. Lett. 2013, 4, 378–382. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Zhang, J.; Zhang, Y.; Deng, Y. Nanoconfined Ionic Liquids. Chem. Rev. 2017, 117, 6755–6833. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Ma, L.; Zhao, Y.; Pan, H.; Tang, H.; Zhang, H. Porous structural effect of carbon electrode formed through one-pot strategy on performance of ionic liquid-based supercapacitors. Chem. Eng. J. 2021, 411, 128573. [Google Scholar] [CrossRef]
- Sharma, S.; Dhattarwal, H.; Kashyap, H. Molecular dynamics investigation of electrostatic properties of pyrrolidinium cation based ionic liquids near electrified carbon electrodes. J. Mol. Liq. 2019, 291, 111269. [Google Scholar] [CrossRef]
- Sharma, S.; Kashyap, H. Interfacial Structure of Pyrrolidinium Cation Based Ionic Liquids at Charged Carbon Electrodes: The Role of Linear and Nonlinear Alkyl Tails. J. Phys. Chem. C 2017, 121, 13202–13210. [Google Scholar] [CrossRef]
- Begic, S.; Jonsson, E.; Chen, F.; Forsyth, M. Molecular dynamics simulations of pyrrolidinium and imidazolium ionic liquids at graphene interfaces. Phys. Chem. Chem. Phys. 2017, 19, 30010–30020. [Google Scholar] [CrossRef]
- Di Lecce, S.; Kornyshev, A.; Urbakh, M.; Bresme, F. Lateral Ordering in Nanoscale Ionic Liquid Films between Charged Surfaces Enhances Lubricity. ACS Nano 2020, 14, 13256–13267. [Google Scholar] [CrossRef]
- Borghi, F.; Podestà, A. Ionic liquids under nanoscale confinement. Adv. Phys. X 2020, 5, 1736949. [Google Scholar] [CrossRef] [Green Version]
- Anaredy, R.S.; Shaw, S.K. Long-Range Ordering of Ionic Liquid Fluid Films. Langmuir 2016, 32, 5147–5154. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Rutland, M.W.; Luo, J.; Atkin, R.; Li, H. Potential-Dependent Superlubricity of Ionic Liquids on a Graphite Surface. J. Phys. Chem. C 2021, 125, 3940–3947. [Google Scholar] [CrossRef]
- Borghi, F.; Piazzoni, C.; Ghidelli, M.; Milani, P.; Podestà, A. Nanoconfinement of Ionic Liquid into Porous Carbon Electrodes. J. Phys. Chem. C 2021, 125, 1292–1303. [Google Scholar] [CrossRef]
- Brutti, S. Pyr1,xTFSI Ionic Liquids (x = 1–8): A Computational Chemistry Study. Appl. Sci. 2020, 10, 8552. [Google Scholar] [CrossRef]
- Cao, X.; He, X.; Wang, J.; Liu, H.; Roser, S.; Rad, B.; Evertz, M.; Streipert, B.; Li, J.; Wagner, R.; et al. High Voltage LiNi0.5Mn1.5O4/Li4Ti5O12 Lithium Ion Cells at Elevated Temperatures: Carbonate- versus Ionic Liquid-Based Electrolytes. ACS Appl. Mater. Interfaces 2016, 8, 25971–25978. [Google Scholar] [CrossRef]
- Banerjee, A.; Shah, J.K. Elucidating the effect of the ionic liquid type and alkyl chain length on the stability of ionic liquid–iron porphyrin complexes. J. Chem. Phys. 2020, 153, 034306. [Google Scholar] [CrossRef]
- Sanchora, P.; Pandey, D.K.; Kagdada, H.L.; Materny, A.; Singh, D.K. Impact of alkyl chain length and water on the structure and properties of 1-alkyl-3-methylimidazolium chloride ionic liquids. Phys. Chem. Chem. Phys. 2020, 22, 17687–17704. [Google Scholar] [CrossRef]
- Garaga, M.N.; Nayeri, M.; Martinelli, A. Effect of the alkyl chain length in 1-alkyl-3-methylimidazolium ionic liquids on inter-molecular interactions and rotational dynamics: A combined vibrational and NMR spectroscopic study. J. Mol. Liq. 2015, 210, 169–177. [Google Scholar] [CrossRef]
- Canongia Lopes, J.N.A.; Pádua, A.A.H. Nanostructural Organization in Ionic Liquids. J. Phys. Chem. B 2006, 110, 3330–3335. [Google Scholar] [CrossRef]
- Holstein, P.; Bender, M.; Galvosas, P.; Geschke, D.; Kärger, J. Anisotropic Diffusion in a Nematic Liquid Crystal—An Electric Field PFG NMR Approach. J. Magn. Reson. 2000, 143, 427–430. [Google Scholar] [CrossRef]
- Umecky, T.; Saito, Y.; Matsumoto, H. Direct Measurements of Ionic Mobility of Ionic Liquids Using the Electric Field Applying Pulsed Gradient Spin−Echo NMR. J. Phys. Chem. B 2009, 113, 8466–8468. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y. Disordering and Reordering of Ionic Liquids under an External Electric Field. J. Phys. Chem. B 2009, 113, 11058–11060. [Google Scholar] [CrossRef] [PubMed]
- Saito, Y.; Hirai, K.; Murata, S.; Kishii, Y.; Kii, K.; Yoshio, M.; Kato, T. Ionic Diffusion and Salt Dissociation Conditions of Lithium Liquid Crystal Electrolytes. J. Phys. Chem. B 2005, 109, 11563–11571. [Google Scholar] [CrossRef] [PubMed]
- Merz, S.; Jakes, P.; Taranenko, S.; Eichel, R.-A.; Granwehr, J. Dynamics of [Pyr13][Tf2N] ionic liquid confined to carbon black. Phys. Chem. Chem. Phys. 2019, 21, 17018–17028. [Google Scholar] [CrossRef]
- Zhu, H.; O’Dell, L.A. Nuclear magnetic resonance characterisation of ionic liquids and organic ionic plastic crystals: Common approaches and recent advances. Chem. Commun. 2021, 57, 5609–5625. [Google Scholar] [CrossRef]
- Forse, A.C.; Griffin, J.M.; Merlet, C.; Bayley, P.M.; Wang, H.; Simon, P.; Grey, C.P. NMR Study of Ion Dynamics and Charge Storage in Ionic Liquid Supercapacitors. J. Am. Chem. Soc. 2015, 137, 7231–7242. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-González, J.; Macías-García, A.; Alexandre-Franco, M.; Mez-Serrano, V. Electrical conductivity of carbon blacks under compression. Carbon 2005, 43, 741. [Google Scholar] [CrossRef]
- Falcon, E.; Castaing, B. Electrical conductivity in granular media and Branly’s coherer: A simple experiment. Am. J. Phys. 2005, 73, 302–307. [Google Scholar] [CrossRef] [Green Version]
- Creyssels, M.; Falcon, E.; Castaing, B. Experiment and Theory of the Electrical Conductivity of a Compressed Granular Metal. AIP Conf. Proc. 2009, 1145, 123–126. [Google Scholar] [CrossRef]
- Watson, A.T.; Chang, C.T.P. Characterizing porous media with NMR methods. Prog. Nucl. Magn. Reson. Spectrosc. 1997, 31, 343–386. [Google Scholar] [CrossRef]
- Haigh, C.W.; Mallion, R.B. Ring current theories in nuclear magnetic resonance. Prog. Nucl. Magn. Reson. Spectrosc. 1979, 13, 303–344. [Google Scholar] [CrossRef]
- Forse, A.C.; Griffin, J.M.; Presser, V.; Gogotsi, Y.; Grey, C.P. Ring Current Effects: Factors Affecting the NMR Chemical Shift of Molecules Adsorbed on Porous Carbons. J. Phys. Chem. C 2014, 118, 7508–7514. [Google Scholar] [CrossRef] [Green Version]
- Kunze, M.; Jeong, S.; Paillard, E.; Schönhoff, M.; Winter, M.; Passerini, S. New Insights to Self-Aggregation in Ionic Liquid Electrolytes for High-Energy Electrochemical Devices. Adv. Energy Mater. 2011, 1, 274–281. [Google Scholar] [CrossRef]
- Ravula, S.; Larm, N.E.; Mottaleb, M.A.; Heitz, M.P.; Baker, G.A. Vapor Pressure Mapping of Ionic Liquids and Low-Volatility Fluids Using Graded Isothermal Thermogravimetric Analysis. ChemEngineering 2019, 3, 42. [Google Scholar] [CrossRef] [Green Version]
- Veroutis, E.; Merz, S.; Eichel, R.A.; Granwehr, J. Intra- and inter-molecular interactions in choline-based ionic liquids studied by 1D and 2D NMR. J. Mol. Liq. 2020, 322, 114934. [Google Scholar] [CrossRef]
- Palumbo, O.; Trequattrini, F.; Appetecchi, G.B.; Paolone, A. Influence of Alkyl Chain Length on Microscopic Configurations of the Anion in the Crystalline Phases of PYR1A-TFSI. J. Phys. Chem. C 2017, 121, 11129–11135. [Google Scholar] [CrossRef]
- Bazant, M.Z.; Storey, B.D.; Kornyshev, A.A. Double Layer in Ionic Liquids: Overscreening versus Crowding. Phys. Rev. Lett. 2011, 106, 046102. [Google Scholar] [CrossRef] [Green Version]
- de Souza, J.P.; Goodwin, Z.A.H.; McEldrew, M.; Kornyshev, A.A.; Bazant, M.Z. Interfacial Layering in the Electric Double Layer of Ionic Liquids. Phys. Rev. Lett. 2020, 125, 116001. [Google Scholar] [CrossRef]
- Bytchenkoff, D.; Rodts, S. Structure of the two-dimensional relaxation spectra seen within the eigenmode perturbation theory and the two-site exchange model. J. Magn. Reson. 2011, 208, 4–19. [Google Scholar] [CrossRef]
- Granwehr, J. Multiplicative or t1 Noise in NMR Spectroscopy. Appl. Magn. Reson. 2007, 32, 113–156. [Google Scholar] [CrossRef]
- Ostroff, E.D.; Waugh, J.S. Multiple Spin Echoes and Spin Locking in Solids. Phys. Rev. Lett. 1966, 16, 1097–1098. [Google Scholar] [CrossRef]
- Borgia, G.C.; Brown, R.J.S.; Fantazzini, P. Uniform-Penalty Inversion of Multiexponential Decay Data. J. Magn. Reson. 1998, 132, 65–77. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Granwehr, J.; Roberts, P.J. Inverse Laplace Transform of Multidimensional Relaxation Data Without Non-Negativity Constraint. J. Chem. Theory Comput. 2012, 8, 3473–3482. [Google Scholar] [CrossRef]
- Washburn, K.E.; Eccles, C.D.; Callaghan, P.T. The dependence on magnetic field strength of correlated internal gradient relaxation time distributions in heterogeneous materials. J. Magn. Reson. 2008, 194, 33–40. [Google Scholar] [CrossRef]
- Carvalho, P.J.; Neves, C.M.S.S.; Coutinho, J.A.P. Surface Tensions of Bis(trifluoromethylsulfonyl)imide Anion-Based Ionic Liquids. J. Chem. Eng. Data 2010, 55, 3807–3812. [Google Scholar] [CrossRef]
- Kolbeck, C.; Lehmann, J.; Lovelock, K.R.J.; Cremer, T.; Paape, N.; Wasserscheid, P.; Fröba, A.P.; Maier, F.; Steinrück, H.P. Density and Surface Tension of Ionic Liquids. J. Phys. Chem. B 2010, 114, 17025–17036. [Google Scholar] [CrossRef] [PubMed]
- Stefan, C.S.; Lemordant, D.; Claude-Montigny, B.; Violleau, D. Are ionic liquids based on pyrrolidinium imide able to wet separators and electrodes used for Li-ion batteries? J. Power Sources 2009, 189, 1174–1178. [Google Scholar] [CrossRef]
- Liu, J.; Song, P.; Ruan, M.; Xu, W. Catalytic properties of graphitic and pyridinic nitrogen doped on carbon black for oxygen reduction reaction. Chin. J. Catal. 2016, 37, 1119–1126. [Google Scholar] [CrossRef]
- Xie, J.; More, K.L.; Zawodzinski, T.A.; Smith, W.H. Porosimetry of MEAs Made by “Thin Film Decal” Method and Its Effect on Performance of PEFCs. J. Electrochem. Soc. 2004, 151, 1841. [Google Scholar] [CrossRef]
- Malinowski, M.; Iwan, A.; Hreniak, A.; Tazbir, I. An anode catalyst support for polymer electrolyte membrane fuel cells: Application of organically modified titanium and silicon dioxide. RSC Adv. 2019, 9, 24428–24439. [Google Scholar] [CrossRef] [Green Version]
- Sepp, S.; Härk, E.; Valk, P.; Vaarmets, K.; Nerut, J.; Jäger, R.; Lust, E. Impact of the Pt catalyst on the oxygen electroreduction reaction kinetics on various carbon supports. J. Solid State Electrochem. 2014, 18, 1223–1229. [Google Scholar] [CrossRef]
- Antxustegi, M.M.; Pierna, A.R.; Ruiz, N. Chemical activation of Vulcan® XC72R to be used as support for NiNbPtRu catalysts in PEM fuel cells. Int. J. Hydrogen Energy 2014, 39, 3978–3983. [Google Scholar] [CrossRef]
- Takasu, Y.; Kawaguchi, T.; Sugimoto, W.; Murakami, Y. Effects of the surface area of carbon support on the characteristics of highly-dispersed Pt-Ru particles as catalysts for methanol oxidation. Electrochim. Acta 2003, 48, 3861–3868. [Google Scholar] [CrossRef]
- Ehrburger-Dolle, F.; Lahaye, J.; Misono, S. Percolation in carbon black powders. Carbon 1994, 32, 1363–1368. [Google Scholar] [CrossRef]
- Pantea, D.; Darmstadt, H.; Kaliaguine, S.; Sümmchen, L.; Roy, C. Electrical conductivity of thermal carbon blacks: Influence of surface chemistry. Carbon 2001, 39, 1147–1158. [Google Scholar] [CrossRef]
- Aubert, G.; Jacquinot, J.F.; Sakellariou, D. Eddy current effects in plain and hollow cylinders spinning inside homogeneous magnetic fields: Application to magnetic resonance. J. Chem. Phys. 2012, 137, 154201. [Google Scholar] [CrossRef]
- Yesinowski, J.P.; Ladouceur, H.D.; Purdy, A.P.; Miller, J.B. Electrical and ionic conductivity effects on magic-angle spinning nuclear magnetic resonance parameters of CuI. J. Chem. Phys. 2010, 133, 234509. [Google Scholar] [CrossRef]
- Alam, T. HR-MAS NMR Spectroscopy in Material Science. Adv. Aspects Spectrosc. 2012, 10, 279–306. [Google Scholar]
- Hayamizu, K.; Tsuzuki, S.; Seki, S.; Fujii, K.; Suenaga, M.; Umebayashi, Y. Studies on the translational and rotational motions of ionic liquids composed of N-methyl-N-propyl-pyrrolidinium (P13) cation and bis(trifluoromethanesulfonyl)amide and bis(fluorosulfonyl)amide anions and their binary systems including lithium salts. J. Chem. Phys. 2010, 133, 194505. [Google Scholar] [CrossRef] [PubMed]
- Senthil Kumar, S.M.; Soler Herrero, J.; Irusta, S.; Scott, K. The effect of pretreatment of Vulcan XC-72R carbon on morphology and electrochemical oxygen reduction kinetics of supported Pd nano-particle in acidic electrolyte. J. Electroanal. Chem. 2010, 647, 211–221. [Google Scholar] [CrossRef]
- Shukla, S.; Bhattacharjee, S.; Weber, A.Z.; Secanell, M. Experimental and Theoretical Analysis of Ink Dispersion Stability for Polymer Electrolyte Fuel Cell Applications. J. Electrochem. Soc. 2017, 164, 600–609. [Google Scholar] [CrossRef]
- Meiboom, S.; Gill, D. Modified Spin-Echo Method for Measuring Nuclear Relaxation Times. Rev. Sci. Instrum. 1958, 29, 688–691. [Google Scholar] [CrossRef] [Green Version]
- Galvosas, P.; Stallmach, F.; Kärger, J. Background gradient suppression in stimulated echo NMR diffusion studies using magic pulsed field gradient ratios. J. Magn. Reson. 2004, 166, 164–173. [Google Scholar] [CrossRef]
- Cotts, R.M.; Hoch, M.J.R.; Sun, T.; Markert, J.T. Pulsed field gradient stimulated echo methods for improved NMR diffusion measurements in heterogeneous systems. J. Magn. Reson. 1989, 83, 252–266. [Google Scholar] [CrossRef]
- Nicotera, I.; Oliviero, C.; Henderson, W.A.; Appetecchi, G.B.; Passerini, S. NMR Investigation of Ionic Liquid−LiX Mixtures: Pyrrolidinium Cations and TFSI- Anions. J. Phys. Chem. B 2005, 109, 22814–22819. [Google Scholar] [CrossRef]
- Callaghan, P.T. Translational Dynamics and Magnetic Resonance: Principles of Pulsed Gradient Spin Echo NMR; Oxford University Press: New York, NY, USA, 2011. [Google Scholar]
- Sørland, G. Dynamic Pulsed-Field-Gradient NMR; Springer: Berlin, Germany, 2014. [Google Scholar]
- Grebenkov, D.S. NMR survey of reflected Brownian motion. Rev. Mod. Phys. 2007, 79, 1077–1137. [Google Scholar] [CrossRef] [Green Version]
- Graf, M.F.; Tempel, H.; Kocher, S.S.; Schierholz, R.; Scheurer, C.; Kungl, H.; Eichel, R.-A.; Granwehr, J. Observing different modes of mobility in lithium titanate spinel by nuclear magnetic resonance. RSC Adv. 2017, 7, 25276–25284. [Google Scholar] [CrossRef] [Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Merz, S.; Wang, J.; Galvosas, P.; Granwehr, J. MAS-NMR of [Pyr13][Tf2N] and [Pyr16][Tf2N] Ionic Liquids Confined to Carbon Black: Insights and Pitfalls. Molecules 2021, 26, 6690. https://doi.org/10.3390/molecules26216690
Merz S, Wang J, Galvosas P, Granwehr J. MAS-NMR of [Pyr13][Tf2N] and [Pyr16][Tf2N] Ionic Liquids Confined to Carbon Black: Insights and Pitfalls. Molecules. 2021; 26(21):6690. https://doi.org/10.3390/molecules26216690
Chicago/Turabian StyleMerz, Steffen, Jie Wang, Petrik Galvosas, and Josef Granwehr. 2021. "MAS-NMR of [Pyr13][Tf2N] and [Pyr16][Tf2N] Ionic Liquids Confined to Carbon Black: Insights and Pitfalls" Molecules 26, no. 21: 6690. https://doi.org/10.3390/molecules26216690
APA StyleMerz, S., Wang, J., Galvosas, P., & Granwehr, J. (2021). MAS-NMR of [Pyr13][Tf2N] and [Pyr16][Tf2N] Ionic Liquids Confined to Carbon Black: Insights and Pitfalls. Molecules, 26(21), 6690. https://doi.org/10.3390/molecules26216690