Pore Development during the Carbonization Process of Lignin Microparticles Investigated by Small Angle X-ray Scattering
Abstract
:1. Introduction
2. Results
2.1. Scanning Electron Microscopy (SEM)
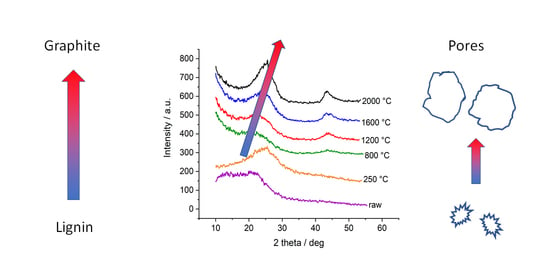
2.2. Wide-Angle X-ray Diffraction (WAXD)
2.3. Small-Angle X-ray Scattering (SAXS)
2.3.1. Submicron Pores, the USAXS Regime
2.3.2. Nanometer-Sized Pores, Classical SAXS Evaluation Strategy
2.3.3. Kratky Plots
2.3.4. Guinier Evaluation
2.3.5. Specific Inner Surface: Porod Evaluation
2.3.6. Nanopore Size Evaluation in Real Space: Radial Distribution Function
2.4. Fourier-Transform Infrared Spectroscopy (FTIR)
3. Discussion
4. Materials and Methods
4.1. Materials
4.2. Lignin Carbonisation
4.3. Characterization of Samples
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Bajwa, D.; Pourhashem, G.; Ullah, A.; Bajwa, S. A concise review of current lignin production, applications, products and their environmental impact. Ind. Crop. Prod. 2019, 139, 111526. [Google Scholar] [CrossRef]
- El Mansouri, N.-E.; Salvadó, J. Analytical methods for determining functional groups in various technical lignins. Ind. Crop. Prod. 2007, 26, 116–124. [Google Scholar] [CrossRef]
- Lora, J.H.; Glasser, W.G. Recent Industrial Applications of Lignin: A Sustainable Alternative to Nonrenewable Materials. J. Polym. Environ. 2002, 10, 39–48. [Google Scholar] [CrossRef]
- Liao, J.J.; Latif, N.H.A.; Trache, D.; Brosse, N.; Hussin, M.H. Current advancement on the isolation, characterization and application of lignin. Int. J. Biol. Macromol. 2020, 162, 985–1024. [Google Scholar] [CrossRef]
- Domínguez-Robles, J.; Cárcamo-Martínez, Á.; Stewart, S.A.; Donnelly, R.F.; Larrañeta, E.; Borrega, M. Lignin for pharmaceutical and biomedical applications-Could this become a reality? Sustain. Chem. Pharm. 2020, 18, 100320. [Google Scholar] [CrossRef]
- Gil-Chávez, J.; Padhi, S.S.P.; Leopold, C.S.; Smirnova, I. Application of Aquasolv Lignin in ibuprofen-loaded pharmaceutical formulations obtained via direct compression and wet granulation. Int. J. Biol. Macromol. 2021, 174, 229–239. [Google Scholar] [CrossRef] [PubMed]
- Baker, D.A.; Rials, T.G. Recent advances in low-cost carbon fiber manufacture from lignin. J. Appl. Polym. Sci. 2013, 130, 713–728. [Google Scholar] [CrossRef]
- Gindl-Altmutter, W.; Köhnke, J.; Unterweger, C.; Gierlinger, N.; Keckes, J.; Zalesak, J.; Rojas, O.J. Lignin-based multiwall carbon nanotubes. Compos. Part. A Appl. Sci. Manuf. 2019, 121, 175–179. [Google Scholar] [CrossRef]
- Han, L.; Nie, X.; Wei, J.; Gu, M.; Wu, W.; Chen, M. Effects of feedstock biopolymer compositions on the physiochemical characteristics of dissolved black carbon from lignocellulose-based biochar. Sci. Total Environ. 2021, 751, 141491. [Google Scholar] [CrossRef] [PubMed]
- Jiang, C.; Bo, J.; Xiao, X.; Zhang, S.; Wang, Z.; Yan, G.; Wu, Y.; Wong, C.; He, H. Converting waste lignin into nano-biochar as a renewable substitute of carbon black for reinforcing styrene-butadiene rubber. Waste Manag. 2020, 102, 732–742. [Google Scholar] [CrossRef] [PubMed]
- Khodabakhshi, S.; Fulvio, P.F.; Andreoli, E. Carbon black reborn: Structure and chemistry for renewable energy harnessing. Carbon 2020, 162, 604–649. [Google Scholar] [CrossRef] [Green Version]
- Härk, E.; Petzold, A.; Goerigk, G.; Risse, S.; Tallo, I.; Härmas, R.; Lust, E.; Ballauff, M. Carbide derived carbons investigated by small angle X-ray scattering: Inner surface and porosity vs. graphitization. Carbon 2019, 146, 284–292. [Google Scholar] [CrossRef]
- Balberg, I. A comprehensive picture of the electrical phenomena in carbon black–polymer composites. Carbon 2002, 40, 139–143. [Google Scholar] [CrossRef]
- Kondrat, S.; Pérez, C.R.; Presser, V.; Gogotsi, Y.; Kornyshev, A.A. Effect of pore size and its dispersity on the energy storage in nanoporous supercapacitors. Energy Environ. Sci. 2012, 5, 6474–6479. [Google Scholar] [CrossRef]
- El Mansouri, N.-E.; Salvadó, J. Structural characterization of technical lignins for the production of adhesives: Application to lignosulfonate, kraft, soda-anthraquinone, organosolv and ethanol process lignins. Ind. Crop. Prod. 2006, 24, 8–16. [Google Scholar] [CrossRef]
- Ma, Y.-Z.; Zheng, D.-F.; Mo, Z.-Y.; Dong, R.-J.; Qiu, X.-Q. Magnetic lignin-based carbon nanoparticles and the adsorption for removal of methyl orange. Colloids Surfaces A Physicochem. Eng. Asp. 2018, 559, 226–234. [Google Scholar] [CrossRef]
- Rodriguez-Mirasol, J.; Cordero, T.; Rodriguez, J.J. Activated carbons from carbon dioxide partial gasification of eucalyptus kraft lignin. Energy Fuels 1993, 7, 133–138. [Google Scholar] [CrossRef]
- Moulefera, I.; García-Mateos, F.J.; Benyoucef, A.; Rosas, J.M.; Rodríguez-Mirasol, J.; Cordero, T. Effect of Co-solution of Carbon Precursor and Activating Agent on the Textural Properties of Highly Porous Activated Carbon Obtained by Chemical Activation of Lignin with H3PO4. Front. Mater. 2020, 7. [Google Scholar] [CrossRef]
- Panduro, E.A.C.; Beuvier, T.; Martínez, M.F.; Hassani, L.; Calvignac, B.; Boury, F.; Gibaud, A. Small-angle X-ray scattering analysis of porous powders of CaCO3. J. Appl. Crystallogr. 2012, 45, 881–889. [Google Scholar] [CrossRef]
- Jafta, C.J.; Petzold, A.; Risse, S.; Clemens, D.; Wallacher, D.; Goerigk, G.; Ballauff, M. Correlating pore size and shape to local disorder in microporous carbon: A combined small angle neutron and X-ray scattering study. Carbon 2017, 123, 440–447. [Google Scholar] [CrossRef]
- Saurel, D.; Segalini, J.; Jauregui, M.; Pendashteh, A.; Daffos, B.; Simon, P.; Casas-Cabanas, M. A SAXS outlook on disordered carbonaceous materials for electrochemical energy storage. Energy Storage Mater. 2019, 21, 162–173. [Google Scholar] [CrossRef]
- Wacha, A.; Varga, Z.; Vainio, U.; Hoell, A.; Bóta, A. Small-angle X-ray scattering experiments and computer simulations to characterise anisotropy of activated carbons prepared from wood. Carbon 2011, 49, 3958–3971. [Google Scholar] [CrossRef] [Green Version]
- Rechberger, M.V.; Kloss, S.; Rennhofer, H.; Tintner, J.; Watzinger, A.; Soja, G.; Lichtenegger, H.; Zehetner, F. Changes in biochar physical and chemical properties: Accelerated biochar aging in an acidic soil. Carbon 2017, 115, 209–219. [Google Scholar] [CrossRef]
- Tintner, J.; Preimesberger, C.; Pfeifer, C.; Soldo, D.; Ottner, F.; Wriessnig, K.; Rennhofer, H.; Lichtenegger, H.C.; Novotny, E.H.; Smidt, E. Impact of Pyrolysis Temperature on Charcoal Characteristics. Ind. Eng. Chem. Res. 2018, 57, 15613–15619. [Google Scholar] [CrossRef]
- Jiang, J.-S.; Guo, R.H.; Chiu, Y.S.; Hua, C.-C. Percolation behaviors of model carbon black pastes. Soft Matter 2018, 14, 9786–9797. [Google Scholar] [CrossRef]
- Köhnke, J.; Fürst, C.; Unterweger, C.; Rennhofer, H.; Lichtenegger, H.C.; Keckes, J.; Emsenhuber, G.; Mahendran, A.R.; Liebner, F.; Gindl-Altmutter, W. Carbon Microparticles from Organosolv Lignin as Filler for Conducting Poly (Lactic Acid). Polymers 2016, 8, 205. [Google Scholar] [CrossRef] [Green Version]
- Köhnke, J.; Rennhofer, H.; Lichtenegger, H.C.; Mahendran, A.R.; Unterweger, C.; Prats-Mateu, B.; Gierlinger, N.; Schwaiger, E.; Mahler, A.K.; Potthast, A.; et al. Electrically Conducting Carbon Microparticles by Direct Carbonization of Spent Wood Pulping Liquor. ACS Sustain. Chem. Eng. 2018, 6, 3385–3391. [Google Scholar] [CrossRef]
- Köhnke, J.; Gierlinger, N.; Prats-Mateu, B.; Unterweger, C.; Solt, P.; Mahler, A.K.; Schwaiger, E.; Liebner, F.; Gindl-Altmutter, W. Comparison of four technical lignins as a resource for electrically conductive carbon particles. BioResources 2018, 14, 1091–1109. [Google Scholar] [CrossRef]
- Hammouda, B. A new Guinier–Porod model. J. Appl. Crystallogr. 2010, 43, 716–719. [Google Scholar] [CrossRef]
- Paris, O.; Peterlik, H. The structure of carbon fibres. In Handbook of Textile Fibre Structure; Springer: Wien, Austria, 2009; pp. 353–377. [Google Scholar]
- Botas, C.; Álvarez, P.; Blanco, C.; Santamaría, R.; Granda, M.; Gutiérrez, M.D.; Rodríguez-Reinoso, F.; Menéndez, R. Critical temperatures in the synthesis of graphene-like materials by thermal exfoliation–reduction of graphite oxide. Carbon 2013, 52, 476–485. [Google Scholar] [CrossRef] [Green Version]
- Ruland, W. Apparent fractal dimensions obtained from small-angle scattering of carbon materials. Carbon 2001, 39, 323–324. [Google Scholar] [CrossRef]
- Svergun, D. Determination of the regularization parameter in indirect-transform methods using perceptual criteria. J. Appl. Crystallogr. 1992, 25, 495–503. [Google Scholar] [CrossRef]
- Franke, D.; Petoukhov, M.V.; Konarev, P.V.; Panjkovich, A.; Tuukkanen, A.; Mertens, H.D.T.; Kikhney, A.G.; Hajizadeh, N.R.; Franklin, J.M.; Jeffries, C.M.; et al. ATSAS 2.8: A comprehensive data analysis suite for small-angle scattering from macromolecular solutions. J. Appl. Crystallogr. 2017, 50, 1212–1225. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feigin, L.A.; Svergun, D.I. Structure Analysis by Small-Angle X-ray and Neutron Scattering; Springer Science and Business Media LLC: New York, NY, USA, 1987; Volume 8, p. 335. [Google Scholar]
- Seehra, M.S.; Pyapalli, S.K.; Poston, J.; Atta-Obeng, E.; Dawson-Andoh, B. Hydrothermal conversion of commercial lignin to carbonaceous materials. J. Indian Acad. Wood Sci. 2015, 12, 29–36. [Google Scholar] [CrossRef]
- Liu, C.; Xu, J.; Hu, J.; Zhang, H.; Xiao, R. Metal Ion-Catalyzed Hydrothermal Liquefaction of Calcium Lignosulfonate in Subcritical Water. Chem. Eng. Technol. 2017, 40, 1092–1100. [Google Scholar] [CrossRef]
- Schwanninger, M.; Rodrigues, J.; Pereira, H.; Hinterstoisser, B. Effects of short-time vibratory ball milling on the shape of FT-IR spectra of wood and cellulose. Vib. Spectrosc. 2004, 36, 23–40. [Google Scholar] [CrossRef]
- Smith, B. Infrared Spectral Interpretation; Apple Academic Press: Boca Raton, FL, USA, 2018; p. 288. [Google Scholar]
- Guo, Y.; Bustin, R. FTIR spectroscopy and reflectance of modern charcoals and fungal decayed woods: Implications for studies of inertinite in coals. Int. J. Coal Geol. 1998, 37, 29–53. [Google Scholar] [CrossRef]
- Gutmann, P.; Moosburger-Will, J.; Kurt, S.; Xu, Y.; Horn, S. Carbonization of polyacrylonitrile-based fibers under defined tensile load: Influence on shrinkage behavior, microstructure, and mechanical properties. Polym. Degrad. Stab. 2019, 163, 174–184. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, G.; Li, Y.; Yao, Y.; Liu, Q.; Xing, B.; Jia, J.; Zhang, C. Structural evolution of porous graphitic carbon nanosheets based on quinonyl decomposition for supercapacitor electrodes. Appl. Surf. Sci. 2021, 537, 147824. [Google Scholar] [CrossRef]
- Belenkov, E.A. Formation of Graphite Structure in Carbon Crystallites. Inorg. Mater. 2001, 37, 928–934. [Google Scholar] [CrossRef]
- Smidt, E.; Meissl, K.; Tintner, J.; Ottner, F. Interferences of carbonate quantification in municipal solid waste incinerator bottom ash: Evaluation of different methods. Environ. Chem. Lett. 2009, 8, 217–222. [Google Scholar] [CrossRef]










| Organosolv | Lignosulfonate | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HTT | 2θ | FWHM | d002 | D002 | S | 2θ | FWHM | d002 | D002 | S |
| °C | ° | ° | Å | nm | ° | ° | Å | nm | ||
| 800 | 22.5 | 10.0 | 3.96 | 0.78 | 2.0 | 22.8 | 9.1 | 3.90 | 0.86 | 2.2 |
| 1200 | 22.7 | 9.7 | 3.92 | 0.80 | 2.0 | 23.2 | 8.8 | 3.84 | 0.88 | 2.3 |
| 1600 | 24.2 | 8.7 | 3.69 | 0.90 | 2.4 | 24.6 | 8.7 | 3.62 | 0.89 | 2.5 |
| 2000 | 25.1 | 6.0 | 3.55 | 1.32 | 3.7 | 25.4 | 6.5 | 3.50 | 1.21 | 3.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rennhofer, H.; Köhnke, J.; Keckes, J.; Tintner, J.; Unterweger, C.; Zinn, T.; Deix, K.; Lichtenegger, H.; Gindl-Altmutter, W. Pore Development during the Carbonization Process of Lignin Microparticles Investigated by Small Angle X-ray Scattering. Molecules 2021, 26, 2087. https://doi.org/10.3390/molecules26072087
Rennhofer H, Köhnke J, Keckes J, Tintner J, Unterweger C, Zinn T, Deix K, Lichtenegger H, Gindl-Altmutter W. Pore Development during the Carbonization Process of Lignin Microparticles Investigated by Small Angle X-ray Scattering. Molecules. 2021; 26(7):2087. https://doi.org/10.3390/molecules26072087
Chicago/Turabian StyleRennhofer, Harald, Janea Köhnke, Jozef Keckes, Johannes Tintner, Christoph Unterweger, Thomas Zinn, Karl Deix, Helga Lichtenegger, and Wolfgang Gindl-Altmutter. 2021. "Pore Development during the Carbonization Process of Lignin Microparticles Investigated by Small Angle X-ray Scattering" Molecules 26, no. 7: 2087. https://doi.org/10.3390/molecules26072087
APA StyleRennhofer, H., Köhnke, J., Keckes, J., Tintner, J., Unterweger, C., Zinn, T., Deix, K., Lichtenegger, H., & Gindl-Altmutter, W. (2021). Pore Development during the Carbonization Process of Lignin Microparticles Investigated by Small Angle X-ray Scattering. Molecules, 26(7), 2087. https://doi.org/10.3390/molecules26072087