Next Article in Journal
Flavonoid Composition and Antibacterial Properties of Crocus sativus L. Petal Extracts
Next Article in Special Issue
Trivalent Polyhedra as Duals of Borane Deltahedra: From Molecular Endohedral Germanium Clusters to the Smallest Fullerenes
Previous Article in Journal
Kukhtin–Ramirez-Reaction-Inspired Deprotection of Sulfamidates for the Synthesis of Amino Sugars
Previous Article in Special Issue
Selenoxides as Excellent Chalcogen Bond Donors: Effect of Metal Coordination
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 28
Issue 1
10.3390/molecules28010183
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Theoretical Investigation of Geometries and Bonding of Indium Hydrides in the In2Hx and In3Hy (x = 0–4,6; y = 0–5) Series

by
Anton S. Pozdeev
,
Pavel Rublev
,
Steve Scheiner
and
Alexander I. Boldyrev
*
Department of Chemistry and Biochemistry, Utah State University, 0300 Old Main Hill, Logan, UT 84322-0300, USA
*
Author to whom correspondence should be addressed.
Molecules 2023, 28(1), 183; https://doi.org/10.3390/molecules28010183
Submission received: 23 November 2022 / Revised: 21 December 2022 / Accepted: 23 December 2022 / Published: 26 December 2022
(This article belongs to the Special Issue Fundamental Aspects of Chemical Bonding)
Browse Figures
Versions Notes

Abstract

:
Boron hydrides have been an object of intensive theoretical and experimental investigation for many decades due to their unusual and somewhat unique bonding patterns. Despite boron being a neighboring element to carbon, boron hydrides almost always form non-classical structures with multi-center bonds. However, we expect indium to form its interesting molecules with non-classical patterns, though such molecules still need to be extensively studied theoretically. In this work, we investigated indium hydrides of In2Hx (x = 0–4,6) and In3Hy (y = 0–5) series via DFT and ab initio quantum chemistry methods, performing a global minimum search, chemical bonding analysis, and studies of their thermodynamical stability. We found that the bonding pattern of indium hydrides differs from the classical structures composed of 1c-2e lone pairs and 2c-2e bonds and the bonding pattern of earlier investigated boron hydrides of the BnHn+2 series. The studied stoichiometries are characterized by multi-center bonds, aromaticity, and the tendency for indium to preserve the 1c-2e lone pair.

Graphical Abstract

1. Introduction

Classical organic chemistry is based on a carbon atom in a valence state of IV. This element usually tends to form 2c-2e bonds with carbon and other elements. Despite boron and carbon being neighboring elements, boron tends to form multi-center bonds [1,2,3]. In particular, it was shown [4] that the BnHn+2 classical structures become less stable along the series because boron avoids expected sp2-hybridization. Despite the rich chemistry of boron hydrides being well-studied [5,6,7,8,9], our knowledge of indium hydride compounds is minimal. Only a small number of indium hydrides and their derivatives have been previously synthesized [10,11] or theoretically investigated [12,13,14]. To our knowledge, almost no conformational search procedures have been applied for indium hydrides with several indium atoms; therefore, the possible non-trivial properties of indium hydrides have been missed.
Being a relatively heavy element, indium atoms have less preference for any type of sp hybridization in hydrogen compounds compared to boron and aluminum. One of the main reasons for this is related to weaker hydrogen–indium orbital overlaps and, therefore, lower interaction: dissociation energies are 3.42 eV and 2.48 eV for B-H and In-H bonds, respectively [15]. Another important reason is a more significant energy gap between 5s and 5p orbitals induced by complete electronic 4d-subshell and the subsequent nucleus charge screening effect. It can be vividly seen from the difference between excitation energies 2Po → 4P of boron and indium atoms [16,17].
Thus, are the indium and boron hydride structures similar or different? Are classical arrangements with only 1c-2e lone pairs and 2c-2e bonds possible for indium hydrides? In this work, we investigated the nature of In2Hx (x = 0–4,6) and In3Hy (y = 0–5) compounds using the Coalescence Kick global optimization techniques, chemical bonding AdNDP analysis, thermodynamic stability toward H2 dissociation to answer the abovementioned questions.

2. Results and Discussions

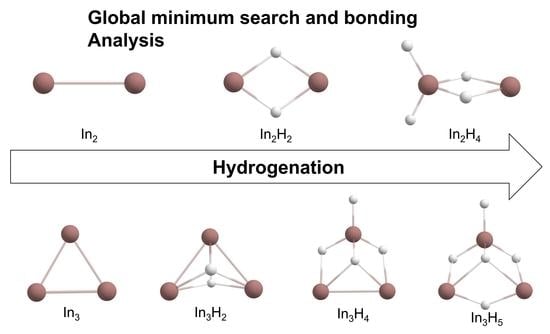
2.1. Global Geometry Optimization and Bonding Analysis

Initially, we performed the CK search for In2Hx and In3Hy (x = 0–4; y = 0–5). The investigated global minima structures are shown in Figure 1. The obtained geometry of the global minimum and energy ordering for low-lying isomers of In2H2 stoichiometry is in entire agreement with the previous investigation [18]. Other low-lying geometries are given in the SI file (Figures S1–S11).
According to the AdNDP analysis, completely unsaturated structures In2 and In3 have similar bonding patterns. In the case of the In2 molecule in the first triplet state, we found two 1c-2e lone pairs, one 2c-1e σ-bond with ON = 0.99e, and one 2c-1e π-bond with ON = 0.99e, where “ON” stands for occupancy number, and “e” reflects that occupancy number is related to the number of electrons.
For In3, we investigated three 1c-2e lone pairs with ON = 1.80e, 3c-2e π-bond with ON = 2.00e, and 3c-1e σ-bond with ON = 0.98e for an unpaired electron. We assign a molecule as being doubly aromatic (i.e., π and σ aromatic; Figure 2). Negative NICSZZ values at different distances from XY-plane can be considered another argument for the aromaticity of In3 [19]. For example, in the case of benzene NICSZZ(0) = −15.199 ppm, NICSZZ(1) = −29.517 ppm, NICSZZ(2) = −17.315 ppm, NICSZZ(3) = −8.014 ppm showing the presence of π-aromaticity. In the case of In3 NICSZZ(0) = −2.146 ppm, NICSZZ(1) = −17.565 ppm, NICSZZ(2) = −17.139 ppm, NICSZZ(3) = −9.760 ppm. For the In3 cluster, the absolute values of NICSZZ(0) and NICSZZ(1) are much smaller than those for benzene. However, the values of NICSZZ(2) and NICSZZ(3) are similar for both molecules; an explanation of the difference may be based on the types of involved orbitals. Benzene is a π aromatic molecule, but In3 is a doubly π and σ aromatic, which indicates the significant difference of NICSZZ(0) and NICSZZ(1) values near the molecular plane, where σ orbitals influence more significantly. It is worth mentioning that an unpaired electron on a σ-like orbital provides a more energetically stable state than a state with an unpaired electron on a π-like orbital. The difference between those electronic states is 4.12 kcal/mol and was obtained using the Δ-CCSD(T)/cc-pVTZ(-PP) level of theory. The same procedure was performed for the In2 molecule. An alternative electronic state with two occupied perpendicular single-occupied 2c-1e π-bonds in the Slater determinant was investigated. This state was less stable by 5.8 kcal/mol at the Δ-CCSD(T)/cc-pVTZ(-PP) level of theory.
Further “hydrogenation” evolution of the In2Hx series reveals some features of indium hydride compounds. Besides 1c-2e lone pairs, in In2H1, we observed 3c-2e In-H-In σ-bond with occupation number ON = 2.00e and 2c-1e In-In σ-bond with ON = 0.98e, but in In2H2 we did not find 2c-2e bonds—only two 1c-2e lone pairs and two 3c-2e In-H-In σ-bonds with ON = 2.00e (Figure 3). Thus, upon “hydrogenation,” indium saves its lone pair instead, forming the 2e-2c classical In-In σ-bond.
In the case of the In2H3 molecule, the AdNDP algorithm allowed us to describe the bonding pattern as three 3c-2e In-H-In σ-bonds with ON = 1.98 e, one 1c-1e unpaired electron with ON = 0.99e on one indium atom, and a 1c-2e lone pair on another indium atom with ON = 1.99e (Figure 4).
According to [4], structure a in Figure 5 is the global minimum of B2H4. In the present study, structure b (Figure 5) is the global minimum for In2H4. Among others, one significant difference between these two molecules is that in the case of B2H4, there is one B-B 2c-2e σ-bond and no 1c-2e lone pairs, but In2H4 has two 3c-2e In-H-In σ-bonds with ON = 1.98e, one 1c-2e lone pair on one indium atom, and no In-In 2c-2e σ-bonds (Figure 6). Moreover, our attempts to find a similar In2H4 structure to the structure in Figure 5a at different theoretical levels were unsuccessful. Thus, this direct comparison of the global minimum structures of B2H4 and In2H4 demonstrates the difference in indium and boron hydride bonding patterns. Both have non-classical structures (i.e., they have delocalized multi-center 2e bonds). However, all boron valence electrons participate in bonding, whereas indium tends to save its lone pair.
An earlier theoretical study of classical and non-classical structures of B2H4 in [4] showed that the non-classical structure is more stable by 2.9 kcal/mol. In this work, the CK search allowed us to find a classical structure for In2H4. The AdNDP analysis reveals that both indium atoms are connected via 2c-2e σ-bonds with ON = 2.00e, and all other In-H bonds are 2c-2e σ-bonds with ON = 1.99e. The energy difference between the classical and non-classical structures is 10.8 kcal/mol at the QRO-CCSD(T)/cc-pVTZ(-PP)//U-TPSSh/def2-TZVPP level of theory. The energy difference is too big to suggest a competition of the classical structure with the global minimum structure. The bonding analysis of the two structures is shown in Figure 6.
Additionally, we decided to investigate the In2H6 species as an analog of the famous diborane molecule. The CK algorithm found only one non-dissociated structure of this stoichiometry; it totally resembles the structure of B2H6. It indicates the stability of the motif. The structure and bonding analysis are presented in Figure 7. We found four 2c-2e In-H σ-bonds with ON = 2.00e and two 3c-2e In-H-In σ-bonds with ON = 1.97e.
In the In3Hy series, we observed the gradual “modification” of the In3 triangular cluster upon “hydrogenation”. In3H and In3H2 have similar structures where each hydrogen is connected with the In3 cluster via 4c-2e In-In-In-H σ -bond with ON = 1.99e (Figure 8). In3H retains σ-aromaticity with an occupation number close to ideal 2.00e. Calculated values of NICSZZ for In3H1 are NICSZZ(0) = +3.804 ppm, NICSZZ(1) = −12.155 ppm, NICSZZ(2) = −14.271 ppm, NICSZZ(3) = −8.235 ppm. A positive value near the center of a molecule with a rapid decrease of NICSzz value as the distance increases can be evidence of σ-aromaticity [20]. Due to hydrogen atom incorporation, the absolute values of NICSzz of In3H1 are smaller than for In3. For In3H2, we found an interesting bonding pattern of 3c-1e In-In-In σ-bond with ON = 1.00e; the AdNDP analysis reveals that it consists of two px orbitals and one perpendicular py orbital.
The 4c-2e In-In-In-H σ-bond appeared to be stable for the In3Hy series. In the In3H3 cluster, the bonding motif of the In3H2 structure was saved, and the third H atom was introduced in the cluster as a bridged atom in a 3c-2e In-H-In σ-bond with ON = 1.99e. This bonding pattern allowed In3H3 to keep three 1c-2e lone pairs on each indium atom with ON = 1.98–1.85e. Further “hydrogenation” leads to In3H4 losing one 4c-2e In-In-In-H σ-bond and one 1c-2e lone pair. It has two 1c-2e lone pairs, one 2c-1e In-In σ-bond with ON = 0.99e, one 2c-1e In-H σ-bond with ON = 0.99e, two 3c-2e In-H-In σ-bonds with ON = 1.99e, and one 4c-2e In-In-In-H σ-bond with ON = 1.97e (Figure 9).
As in the case of In2H4 and B2H4, the global minimum structures of In3H5 and B3H5 [4] are different. Both systems are presented in Figure 10. B3H5 has three 2c-2e B-H terminal σ-bonds, two bridged B-H-B σ-bonds, and three B atoms that are bonded via 3c-2e B-B-B σ-bond and a 3c-2e B-B-B π-bond, so there are no 1c-2e lone pairs again. In In3H5, two indium atoms save 1c-2e lone pairs; there is one In-H 2c-2e terminal σ- bond with ON = 1.99e, three bridged 3c-2e In-H-In σ-bonds with ON = 1.98–1.97e, and one 4c-2e In-In-In-H σ-bond with ON = 1.96e (Figure 11). Thus, for boron clusters, aromaticity is found for both saturated and non-saturated structures [21], but for indium, we observed aromaticity only for the most unsaturated hydrides. It is another demonstration of the difference between the patterns of boron and indium hydrides.
The low-lying classical In3H5 structure (Figure 11) is about 17.2 kcal/mol higher than the global minimum structure; this corresponds to the trend previously observed for BnHn+2 series [4] (i.e., classical structures become progressively less stable along the series). The bonding pattern of the classical structure of In3H5 is similar to what was observed for the classical structure of In2H4; it has two types of bonds—2c-2e In-H σ-bond with ON = 1.99e and 2c-2e In-In σ bond with ON = 1.99e.

2.2. Thermodynamic Stability Observation

To estimate the thermodynamics stability of the indium hydrides toward H2 dissociation, we calculated the potential energy difference of locally reoptimized structures at QRO-CCSD(T)/cc-pVTZ(-PP)//U-TPSSh/def2-TZVPP level of theory. The results of these calculations are shown in Table 1.
According to the data, almost all indium hydrides are stable toward H2 dissociation, except In2H3, In2H6, and In3H4. However, even in the case of these molecules, the ΔE of the dissociation reaction is very small.

3. Theoretical Methods

The global minimum search was carried out using the Coalescence Kick (CK) algorithm written by Averkiev [22,23] to find a global minimum and corresponding low-lying isomers for In2Hx and In3Hy (x = 0–4,6; y = 0–5). The basic workflow of the CK algorithm consists of (1) the random placing of atoms in a sizeable Cartesian box, (2) the shift of atoms toward the center of mass until they coalesce up to the pairwise sums of pre-defined covalent radii of atoms, (3) the standard local geometry optimization using Ab Initio, DFT, or semi-empirical approach. The CK procedure is repeated several thousand times to obtain an adequate statistic, and the most stable structure is implied to be a global minimum. The CK original code is available online at the open repository [24].
All calculations utilizing the CK procedure were carried out using unrestricted Kohn–Sham formalism with density functional MN-15. It was chosen for its appropriate applicability to various electronic structure problems, including multireference behavior [25]. The LANL2DZ basis set was chosen for its balance of speed and accuracy [26]; additionally, the Hay–Wadt pseudopotential was applied to indium atoms to account for scalar relativity correction [27]. The specific generation size of random structures for the CK method for each stoichiometry is shown in the SI file (Table S1). Gaussian 16 was used as the main driver for the local optimization step [28] in the CK algorithm.
After the CK global minimum search, all obtained low-lying isomers in the 15 kcal/mol energy window from the global minimum were reoptimized with a more accurate def2-TZVPP basis set [29] and TPSSh density functional [30], which tends to provide better energy ordering of isomers but cannot be generously applied to any electronic problem. Obtained local minima were verified by nuclear Hessian calculation with the same method and basis set. The re-optimization step and all subsequent single-point calculations utilized the ORCA 5.03 suite [31,32].
Using obtained local minima geometries, single point energies were recalculated at the CCSD(T) level of theory with the cc-pVTZ [33] basis set on hydrogen atoms and the cc-pVTZ-PP basis set on indium atoms complemented with the SK-MCDHF-RSC pseudopotential [34,35]. The CCSD(T) approach is a gold standard for the accurate prediction of energy ordering and provides meaningful results only in conjunction with large basis sets. Quasi-restricted orbitals formalism (QRO-CCSD(T)) was employed to eliminate the influence of spin-contamination in the open-shell coupled clusters calculations. In addition, all CCSD(T) reference UHF wavefunctions were tested using UHF/UHF stability analysis based on the CIS method [36].
Thus, the final energy ordering of low-lying isomers was estimated using QRO-CCSD(T)/cc-pVTZ energies and U-TPSSh/def2-TZVPP geometries and corresponding zero-point energy corrections (ZPE). This calculation scheme will be denoted as “QRO-CCSD(T)/cc-pVTZ(-PP)//U-TPSSh/def2-TZVPP”.
It should be outlined that, due to the adiabatic treatment of the potential energy surface, the CK algorithm can be applied only for one spin state at a time. For stoichiometry with an even number of electrons, we chose a singlet multiplicity in the algorithm; for an odd number of electrons, we decided to use a doublet multiplicity. To verify that other spin states are not global minima, they were locally reoptimized in the corresponding triplet or quartet multiplicities at the U-TPSSh/def2-TZVPP level of theory. Further single point energy calculations at the QRO-CCSD(T)/cc-pVTZ(-PP) theoretical level demonstrated that in the case of all stoichiometries, except In2 and In3H1, the energy difference between a global minimum structure in the lowest spin multiplicity and a corresponding low-lying structure in triplet (or quartet) multiplicity was at least 15–30 kcal/mol. That allowed us to justify the choice of multiplicity in the CK algorithm.
In the case of In2, we found the triplet state to be more stable than the singlet state by 6.8 kcal/mol, which is in accordance with previous findings [37]. For In3H1, the singlet state is more stable than the locally reoptimized triplet state; however, the energy difference between them is relatively small (~2.5 kcal/mol). Therefore, we carried out an additional CK search to find the actual global minimum of the triplet state. In this way, we found the singlet state still to be more stable than the triplet state by 1.4 kcal/mol at the QRO-CCSD(T)/cc-pVTZ(-PP) level of theory. The energy differences between spin states are provided in the SI file (Table S2).
Chemical bonding for all global minimum isomers for each stoichiometry was analyzed using the adaptive natural density partitioning (AdNDP) algorithm implemented in AdNDP 2.0 [38,39] as an effective method of deciphering bonding in molecular clusters with untrivial electron delocalization. This approach is based on the Lewis idea that an electron pair is the main bonding element. The algorithm leads to the partitioning of the electron density into elements with the lowest symmetry-appropriate number of atomic centers per electron pair, which allows for the representation of an electronic structure as n-center two-electron bonds (nc-2e, n is an interval from one to the total number of atoms participating in the bond). The same procedure may be applied to open-shell systems and may recover nc-1e bonding elements. Despite the usage of the “electron pair idea,” AdNDP and its ideological predecessor NBO analyses based on the density matrix representation of the wavefunction; therefore, near doubly occupied bonding elements are obtained through chains of similarity or unitary transformations of canonical KS “wavefunction,” which is represented by single Slater determinant. Thus, the limit of two-electron occupancy per bonding element is not arbitrary and is dictated by Pauli’s exclusion principle for fermions and the primary modern approach to compose many-body wavefunctions. Thus, the AdNDP algorithm recovers classical Lewis bonding elements (i.e., 1c-2e lone-pairs and 2c-2e bonds) and the delocalized bonding elements similar to occupied canonical molecular orbitals, which are the most appropriate for this study. In this work, the density matrices for the AdNDP were obtained at the U-TPSSh/def2-TZVPP level of theory. Visualization of molecular structures and AdNDP orbitals was performed with ChemCraft [40].
In addition, the AdNDP algorithm may show molecules’ potential aromatic or anti-aromatic character. To verify it, the components of nucleus-independent chemical shift (NICSzz) corresponding to the principal z-axis perpendicular to a ring plane may be used as a good characteristic of aromaticity [40]. We calculated NICSzz(R) values (R means the distance from the center of a ring in Å units) at the TPSSh/def2-TZVPP level of theory.

4. Conclusions

In this work, we used the CK algorithm for the global minimum search for In2Hx and In3Hy (x = 0–4,6; y = 0–5) stoichiometry. Found global minimum geometries were used to investigate the structural evolution of In2 and In3 clusters under “hydrogenation”. We also investigated their chemical bonding pattern using the AdNDP algorithm and tested their thermodynamic stability toward H2 dissociation. Our analysis revealed that both boron and indium hydrates have non-classical structures with multi-center 2e bonds, and they are much more stable than classical structures with sp2 hybridization. Indium hydrides are characterized by non-intuitive global minimum geometries, where indium tends to save its lone pair even if it leads to the loss of a classical 2c-2e bond. Some unsaturated indium clusters have aromatic properties. We want to emphasize that the revealed difference between boron and indium hydrides is closely related to the difference in the fundamental properties of boron and indium atoms: higher excitation energy of indium atoms and less energetically favorable indium–hydrogen bond formation.
We hope this work will inspire further theoretical and experimental investigation of these exotic indium species.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules28010183/s1, Table S1. Population size used for CK algorithm for In2Hx and In3Hy (x = 0–4,6; y = 0–5) stoichiometries; Table S2. Spin-state energy difference; Table S3. In2Hx and In3Hy (x = 0–4,6; y = 0–5) global minimum geometries for singlet and doublet states found the lowest lying isomers for triplet and quartet states (XYZ coordinates); Table S4. NICSzz values; Figures S1–S11. Global minimum geometries and low-lying geometries with corresponding relative energies for each In2Hx and In3Hy (x = 0–4,6; y = 0–5) stoichiometry, chemical bonding patterns for global minimum geometries.

Author Contributions

Conceptualization: A.S.P., S.S., P.R. and A.I.B.; methodology: A.S.P., S.S., P.R. and A.I.B.; writing—original draft preparation: A.S.P., S.S., P.R. and A.I.B.; writing—review, and editing: S.S. and A.I.B.; visualization: A.S.P. All authors have read and agreed to the published version of the manuscript.

Funding

The research was funded by the R. Gaurth Hansen Professorship fund to A.I.B.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data that support the findings of this study are available from the corresponding authors upon reasonable request.

Acknowledgments

The support and resources from the Centre for High Performance Computing at the University of Utah are gratefully acknowledged.

Conflicts of Interest

The authors declare no conflict of interest.

Sample Availability

Samples of the compounds are not available from the authors.

References

  1. Lipscomb, W.N. Boron Hydrides; Benjamin Inc.: New York, NY, USA, 1963. [Google Scholar]
  2. Muetterties, E.L. Boron Hydride Chemistry; Academic Press: New York, NY, USA, 1975. [Google Scholar]
  3. Pan, S.; Barroso, J.; Jalife, S.; Heine, T.; Asmis, K.R.; Merino, G. Fluxional Boron Clusters: From Theory to Reality. Acc. Chem. Res. 2019, 52, 2732–2744. [Google Scholar] [CrossRef] [PubMed]
  4. Osorio, R.; Olson, J.K.; Tiznado, W.; Boldyrev, A.I. Analysis of Why Boron Avoids sp2 Hybridization and Classical Structures in the BnHn+2 Series. Eur. J. Chem. 2012, 18, 9677–9681. [Google Scholar] [CrossRef] [PubMed]
  5. Cho, B.T. Recent development and improvement for Boron hydride-based catalytic asymmetric reduction of unsymmetrical ketones. Chem. Soc. Rev. 2009, 38, 443–452. [Google Scholar] [CrossRef] [PubMed]
  6. Sivaev, I.B.; Bregadze, V.V. Polyhedral Boranes for Medical Applications: Current Status and prospects. Eur. J. Inorg. Chem. 2009, 2009, 1433–1450. [Google Scholar] [CrossRef]
  7. Fakioğlu, E.; Yürüm, Y.; Veziroğlu, T.N. A review of hydrogen storage systems based on Boron and its compounds. Int. J. Hydrogen Energy 2004, 29, 1371–1376. [Google Scholar] [CrossRef]
  8. Sergeeva, A.P.; Popov, I.A.; Piazza, Z.A.; Li, W.L.; Romanescu, C.; Wang, L.S.; Boldyrev, A.I. Understanding Boron through Size-Selected Clusters: Structure, Chemical Bonding, and Fluxionality. Acc. Chem. Res. 2014, 47, 1349–1358. [Google Scholar] [CrossRef]
  9. Jian, T.; Chen, X.; Li, S.D.; Boldyrev, A.I.; Li, J.; Wang, L.S. Probing the structures and bonding of size-selected Boron and doped-Boron clusters. Chem. Soc. Rev. 2019, 48, 3550–3591. [Google Scholar] [CrossRef]
  10. Wiberg, E.; Schmidt, M.Z. Uber Wasserstoff-Verbindungen des Indiums. Z. Nat. B 1957, 12, 54. [Google Scholar] [CrossRef]
  11. Miyai, T.; Inoue, K.; Yasuda, M.; Shibata, I.; Baba, A. Preparation of a novel Indium hydride and application to practical organic synthesis. Tetrahedron Lett. 1998, 39, 1929–1932. [Google Scholar] [CrossRef]
  12. Hunt, P.; Schwerdtfeger, P. Are the Compounds InH3 and TlH3 Stable Gas Phase or Solid State Species? Inorg. Chem. 1996, 35, 2085–2088. [Google Scholar] [CrossRef]
  13. Schwerdtfeger, P.; Heath, G.A.; Dolg, M.; Bennett, M.A. Low Valencies and Periodic Trends in Heavy Element Chemistry. A Theoretical Study of Relativistic Effects and Electron Correlation Effects in Group 13 and Period 6 Hydrides and Halides. Am. Chem. Soc. 1992, 114, 7518–7527. [Google Scholar] [CrossRef]
  14. Liu, Y.; Duan, D.; Tian, F.; Liu, H.; Wang, C.; Huang, X.; Li, D.; Ma, Y.; Liu, B.; Cui, T. Pressure-Induced Structures and Properties in Indium Hydrides. Inorg. Chem. 2015, 54, 9924–9928. [Google Scholar] [CrossRef] [PubMed]
  15. Huber, K.P.; Herzberg, G. Chapter IV Constants of Diatomic Molecules. In Molecular Spectra and Molecular Structure, 1st ed.; Springer: New York, NY, USA, 1979. [Google Scholar]
  16. Edlén, B.; Ölme, A.; Herzberg, G.; Johns, J.W.C. Ionization Potential of Boron, and the Isotopic and Fine Structure of 2s2p2.2D. J. Opt. Soc. Am. 1970, 60, 889. [Google Scholar] [CrossRef]
  17. Paschen, F.; Campbell, J.S. Das erste Funkenspektrum des Indiums in II. Ann. Phys. 1938, 423, 29–75. [Google Scholar] [CrossRef]
  18. Mulla, H.F.; Franke, P.R.; Sargenta, C.; Douberlya, G.E.; Turney, J.M.; Schaefer, H.F., III. Four isomers of In2H2: A careful comparison between theory and experiment. Mol. Phys. 2021, 119, e1979675. [Google Scholar] [CrossRef]
  19. Báez-Grezab, R.; Ruizc, L.; Pino-Rios, R.; Tiznado, W. Which NICS method is most consistent with ring current analysis? Assessment in simple monocycles. RSC Adv. 2018, 8, 13446–13453. [Google Scholar] [CrossRef] [Green Version]
  20. Chen, Z.; Wannere, C.S.; Corminboeuf, C.; Puchta, R.; Schleyer, P.V.R. Nucleus-Independent Chemical Shifts (NICS) as an Aromaticity Criterion. Chem. Rev. 2005, 105, 3842–3888. [Google Scholar] [CrossRef]
  21. Sergeeva, A.P.; Averkiev, B.B.; Zhai, H.-J.; Boldyrev, A.I.; Wang, L.S. All-Boron analogues of aromatic hydrocarbons: B17− and B18−. J. Chem. Phys. 2011, 134, 224304. [Google Scholar] [CrossRef] [Green Version]
  22. Alexandrova, A.N.; Boldyrev, A.I.; Zhai, H.J.; Wang, L.S. All-Boron aromatic clusters as potential new inorganic ligands and building blocks in chemistry. Coord. Chem. Rev. 2006, 250, 2811–2866. [Google Scholar] [CrossRef]
  23. Saunders, M. Stochastic search for isomers on a quantum mechanical surface. J. Comput. Chem. 2004, 25, 621–626. [Google Scholar] [CrossRef]
  24. Coalescence Modification to Saunders KICK Version. Available online: https://kick.science/KICK_Saunders_coalescence.html (accessed on 25 November 2022).
  25. Yu, H.S.; He, X.; Li, S.L.; Truhlar, D.G. MN15: A Kohn–Sham global-hybrid exchange–correlation density functional with broad accuracy for multi-reference and single-reference systems and noncovalent interactions. Chem. Sci. 2016, 7, 5032–5051. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  26. Dunning, T.H.; Hay, P.J. Modern Theoretical Chemistry; Schaefer, H.F., III, Ed.; Plenum: New York, NY, USA, 1977; Volume 3, pp. 1–28. [Google Scholar]
  27. Wadt, W.R.; Hay, P.J. Ab initio effective core potentials for molecular calculations. Potentials for main group elements Na to Bi. J. Chem. Phys. 1985, 82, 284. [Google Scholar] [CrossRef]
  28. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision B.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
  29. Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
  30. Tao, J.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the Density Functional Ladder: Nonempirical Meta–Generalized Gradient Approximation Designed for Molecules and Solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef] [Green Version]
  31. Neese, F. The ORCA program system. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
  32. Neese, F. Software update: The ORCA program system—Version 5.0. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2021, 12, e1606. [Google Scholar] [CrossRef]
  33. Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms Boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007. [Google Scholar] [CrossRef]
  34. Metz, B.; Stoll, H. Small-core multiconfiguration-Dirac–Hartree–Fock-adjusted pseudopotentials for post-d main group elements: Application to PbH and PbO. J. Chem. Phys. 2000, 113, 2563. [Google Scholar] [CrossRef]
  35. Peterson, K.A. Systematically convergent basis sets with relativistic pseudopotentials. I. Correlation consistent basis sets for the post-d group 13–15 elements. J. Chem. Phys. 2003, 119, 11099. [Google Scholar] [CrossRef] [Green Version]
  36. Bauernschmitt, R.; Ahlrichs, R. Stability analysis for solutions of the closed shell Kohn–Sham equation. J. Chem. Phys. 1996, 104, 9047. [Google Scholar] [CrossRef]
  37. Balasubramanian, K.; Li, J. Spectroscopic properties and potential energy surfaces of In2. J. Chem. Phys. 1998, 88, 4979. [Google Scholar] [CrossRef]
  38. Tkachenko, N.V.; Boldyrev, A.I. Chemical bonding analysis of excited states using the Adaptive Natural Density Partitioning method. Phys. Chem. Chem. Phys. 2019, 21, 9590–9596. [Google Scholar] [CrossRef] [PubMed]
  39. Zubarev, D.Y.; Boldyrev, A.I. Developing paradigms of chemical bonding: Adaptive natural density partitioning. Phys. Chem. Chem. Phys. 2008, 10, 5207–5217. [Google Scholar] [CrossRef] [PubMed]
  40. Chemcraft. Available online: http://www.chemcraftprog.com (accessed on 25 November 2022).
Molecules 28 00183 g001 550
Figure 1. Global minimum structures of (a) In2Hx (x = 0–4), (b) In3Hy (y = 0–5).
Figure 1. Global minimum structures of (a) In2Hx (x = 0–4), (b) In3Hy (y = 0–5).
Molecules 28 00183 g001
Molecules 28 00183 g002 550
Figure 2. The chemical bonding pattern of In2 and In3 global minimum structures obtained by AdNDP analysis.
Figure 2. The chemical bonding pattern of In2 and In3 global minimum structures obtained by AdNDP analysis.
Molecules 28 00183 g002
Molecules 28 00183 g003 550
Figure 3. The chemical bonding pattern of In2H1 and In2H2 global minimum structures obtained by AdNDP analysis.
Figure 3. The chemical bonding pattern of In2H1 and In2H2 global minimum structures obtained by AdNDP analysis.
Molecules 28 00183 g003
Molecules 28 00183 g004 550
Figure 4. The chemical bonding pattern of the In2H3 global minimum structure obtained by AdNDP analysis.
Figure 4. The chemical bonding pattern of the In2H3 global minimum structure obtained by AdNDP analysis.
Molecules 28 00183 g004
Molecules 28 00183 g005 550
Figure 5. The comparison of the global minimum structures for (a) B2H4 (according to [4]) and (b) In2H4.
Figure 5. The comparison of the global minimum structures for (a) B2H4 (according to [4]) and (b) In2H4.
Molecules 28 00183 g005
Molecules 28 00183 g006 550
Figure 6. The chemical bonding pattern of In2H4―non-classical structure (global minimum) and classical structure obtained by AdNDP analysis.
Figure 6. The chemical bonding pattern of In2H4―non-classical structure (global minimum) and classical structure obtained by AdNDP analysis.
Molecules 28 00183 g006
Molecules 28 00183 g007 550
Figure 7. The chemical bonding pattern of the In2H6 global minimum structure obtained by AdNDP analysis.
Figure 7. The chemical bonding pattern of the In2H6 global minimum structure obtained by AdNDP analysis.
Molecules 28 00183 g007
Molecules 28 00183 g008 550
Figure 8. The chemical bonding pattern of In3H1 and In3H2 obtained by AdNDP analysis.
Figure 8. The chemical bonding pattern of In3H1 and In3H2 obtained by AdNDP analysis.
Molecules 28 00183 g008
Molecules 28 00183 g009 550
Figure 9. The chemical bonding pattern of In3H3 and In3H4 obtained by AdNDP analysis.
Figure 9. The chemical bonding pattern of In3H3 and In3H4 obtained by AdNDP analysis.
Molecules 28 00183 g009
Molecules 28 00183 g010 550
Figure 10. The comparison of the global minimum structures for (a) B3H5 (according to [4]) and (b) In3H5.
Figure 10. The comparison of the global minimum structures for (a) B3H5 (according to [4]) and (b) In3H5.
Molecules 28 00183 g010
Molecules 28 00183 g011 550
Figure 11. The chemical bonding pattern of In3H5―non-classical structure (global minimum) and classical structure.
Figure 11. The chemical bonding pattern of In3H5―non-classical structure (global minimum) and classical structure.
Molecules 28 00183 g011
Table
Table 1. Analysis of thermodynamic stability toward H2 dissociation at the QRO-CCSD(T)/cc-pVTZ(-PP)//U-TPSSh/def2-TZVPP level of theory.
Table 1. Analysis of thermodynamic stability toward H2 dissociation at the QRO-CCSD(T)/cc-pVTZ(-PP)//U-TPSSh/def2-TZVPP level of theory.
StoichiometryDecomposition ProductStabilityEproducts − Ereagents, kcal/mol
In2H2In2 + H2stable25.2
In2H3In2H + H2unstable−0.1
In2H4In2H2 + H2In2 + 2H2stable
stable		4.8
30.0
In2H6In2H4 + H2In2H2 + 2H2In2 + 3H2unstable
stable
stable		−2.1
2.7
27.9
In3H2In3 + H2stable12.1
In3H3In3H + H2stable12.2
In3H4In3H2 + H2In3 + 2H2unstable
stable		−0.5
11.6
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Pozdeev, A.S.; Rublev, P.; Scheiner, S.; Boldyrev, A.I. Theoretical Investigation of Geometries and Bonding of Indium Hydrides in the In2Hx and In3Hy (x = 0–4,6; y = 0–5) Series. Molecules 2023, 28, 183. https://doi.org/10.3390/molecules28010183

AMA Style

Pozdeev AS, Rublev P, Scheiner S, Boldyrev AI. Theoretical Investigation of Geometries and Bonding of Indium Hydrides in the In2Hx and In3Hy (x = 0–4,6; y = 0–5) Series. Molecules. 2023; 28(1):183. https://doi.org/10.3390/molecules28010183

Chicago/Turabian Style

Pozdeev, Anton S., Pavel Rublev, Steve Scheiner, and Alexander I. Boldyrev. 2023. "Theoretical Investigation of Geometries and Bonding of Indium Hydrides in the In2Hx and In3Hy (x = 0–4,6; y = 0–5) Series" Molecules 28, no. 1: 183. https://doi.org/10.3390/molecules28010183

APA Style

Pozdeev, A. S., Rublev, P., Scheiner, S., & Boldyrev, A. I. (2023). Theoretical Investigation of Geometries and Bonding of Indium Hydrides in the In2Hx and In3Hy (x = 0–4,6; y = 0–5) Series. Molecules, 28(1), 183. https://doi.org/10.3390/molecules28010183

Article Metrics

Back to TopTop