Main-Group Metal Complexes of Benzene: Predicted Features of Stabilization and Isomerization
Abstract
:1. Introduction
2. Results and Discussion
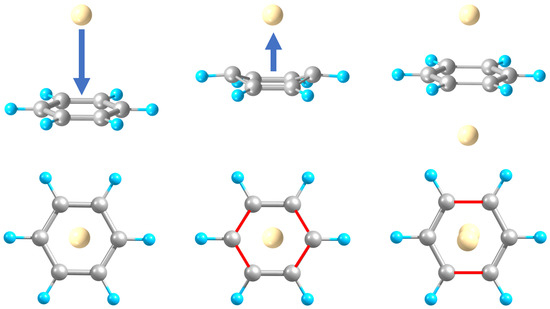
2.1. Structures and Stabilities
2.2. Charge Distributions and Polarities
2.3. Aromaticity Evaluation
2.4. Vibrations and Simulated IR Spectra
2.5. Other Electronic States
3. Computational Methods and Tools
4. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Hatua, K.; Nandi, P.K. Second hyperpolarizability of delta shaped disubstituted acetylene complexes of beryllium, magnesium, and calcium. J. Molec. Model. 2015, 21, 254. [Google Scholar] [CrossRef]
- Hatua, K.; Nandi, P.K. Hyper Second hyperpolarizability of multimetallocenes [Cp-Mn-Cp] of Be, Mg and Ca. J. Theor. Comp. Chem. 2015, 14, 1550002. [Google Scholar] [CrossRef]
- Pandey, A.P.; Padidela, U.K.; Thulasiraman, L.K.; Sethu, R.; Vairaprakash, P.; Thimmakondu, V.S. MgC6H2 Isomers: Potential Candidates for Laboratory and Radioastronomical Studies. J. Phys. Chem. A 2020, 124, 7518–7525. [Google Scholar] [CrossRef]
- Thimmakondu, V.S. MgC2H2 isomers—Simple penta-atomic molecules missing in the laboratory. Chem. Phys. 2020, 538, 110899. [Google Scholar] [CrossRef]
- Tabares, A.A.; Zoellner, R.W. Magnesepin, 1,4-dimagnesocin, 1,4,7-trimagnesonin, and their C6H6Mgn, n = 1–3, isomers: A density functional computational investigation. Heteroatom Chem. 2017, 28, e21355. [Google Scholar] [CrossRef]
- Naumkin, F.Y. Complexes of Be and Mg with unsaturated hydrocarbon molecules: Inter-and intramolecular cooperativity of binding. Chem. Phys. Lett. 2010, 499, 203–208. [Google Scholar] [CrossRef]
- Naumkin, F.Y.; Fisher, K. Small metal–organic molecular sandwiches: Versatile units for induced structure manipulation. Chem. Phys. Lett. 2013, 590, 52–57. [Google Scholar] [CrossRef]
- Boronski, J.T.; Crumpton, A.E.; Wales, L.L.; Aldridge, S. Diberyllocene, a stable compound of Be(I) with a Be–Be bond. Science 2023, 380, 1147–1149. [Google Scholar] [CrossRef]
- Dong, F.; Xie, Y.; Bernstein, E.R. Experimental and theoretical studies of neutral MgmCnHx and BemCnHx clusters. J. Chem. Phys. 2011, 135, 054307. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ferro, Y.; Fernandez, N.; Allouche, A.; Linsmeier, C. Adsorption of beryllium atoms and clusters both on graphene and in a bilayer of graphite investigated by DFT. J. Phys. Cond. Matt. 2013, 25, 015002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pablo, A.; Denis, P.A.; Iribarne, F. Theoretical investigation on the interaction between Be, Mg and Ca with benzene, coronene, cirumcoronene and graphene. Chem. Phys. 2014, 430, 1–6. [Google Scholar]
- Ullah, S.; Denis, P.A.; Sato, F. Coupled cluster investigation of the interaction of Be, Mg and Ca with pyridine: Implications for the adsorption on nitrogen-doped graphene. Comp. Theor. Chem. 2019, 1150, 57–62. [Google Scholar] [CrossRef]
- Valiev, M.; Bylaska, E.J.; Govind, N.; Kowalski, K.; Straatsma, T.P.; van Dam, H.J.J.; Wang, D.; Nieplocha, J.; Apra, E.; Windus, T.L.; et al. NWChem: A comprehensive and scalable open-source solution for large scale molecular simulations. Comput. Phys. Commun. 2010, 181, 1477–1489. [Google Scholar] [CrossRef] [Green Version]
- Schuchardt, K.L.; Didier, B.T.; Elsethagen, T.; Sun, L.; Gurumoorthi, V.; Chase, J.; Li, J.; Windus, T.L. Basis Set Exchange: A Community Database for Computational Sciences. J. Chem. Inf. Model. 2007, 47, 1045–1052. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Linstrom, P.J.; Mallard, W.G. (Eds.) NIST Chemistry WebBook, NIST Standard Ref. Database Number 69; NIST: Gaithersburg, MD, USA, 2023. Available online: https://webbook.nist.gov/chemistry/ (accessed on 16 July 2023).
- Halfen, D.T.; Apponi, A.J.; Ziurys, L.M. Laboratory Detection and Pure Rotational Spectrum of the CaC Radical (X 3Σg̶ ). Astrophys. J. 2002, 577, L67–L70. [Google Scholar] [CrossRef]
- Boys, S.F.; Bernardi, F. The Calculation of Small Molecular Interactions by the Differences of Separate Total Energies. Some Procedures with Reduced Errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Reed, A.E.; Robert, B.; Weinstock, R.B.; Weinhold, F. Natural population analysis. J. Chem. Phys. 1985, 83, 735–746. [Google Scholar] [CrossRef]
- Nikolaienko, T.Y.; Bulavin, L.A.; Hovorun, D.M. JANPA: An open source cross-platform implementation of the Natural Population Analysis on the Java platform. Comput. Theor. Chem. 2014, 1050, 15–22. [Google Scholar] [CrossRef]
- Krygowski, T.M. Crystallographic studies of inter- and intramolecular interactions reflected in aromatic character of .pi.-electron systems. J. Chem. Inf. Comp. Sci. 1993, 33, 70–78. [Google Scholar] [CrossRef]
- Giambiagi, M.; de Giambiagi, M.S.; Mundim, K.C. Definition of a multicenter bond index. Struct. Chem. 1990, 1, 423–427. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]



| System | De †/eV | Re (M-C)/Å | Re (C-C) | φ (C4) /deg | Re (M-M) |
|---|---|---|---|---|---|
| Be-Bz (p) | 0.11 | 3.13 | 1.39 | 180 | |
| Be-Bz (c) | 0.20 | 1.76, 1.81, 2.50 | 1.35–1.48 | 130 | |
| Mg-Bz (p) | 0.11 | 3.40–3.43 | 1.39 | 180 | |
| Ca-Bz (p) | 0.13 | 3.50–3.51 | 1.39 | 180 | |
| Ca-Bz (c) | −0.23 | 2.48, 2.73 | 1.37, 1.44 | 151 | |
| Sr-Bz (p) | 0.12 | 3.41–3.47 | 1.39 | 180 | |
| Sr-Bz (c) | −0.22 | 2.62, 2.86 | 1.37, 1.44 | 153 | |
| Ba-Bz (p) | 0.20 | 3.32 | 1.39 | 180 | |
| Ba-Bz (c) | 0.33 | 2.64, 2.86 | 1.37, 1.45 | 154 | |
| Be-Bz-Be (p) | 0.21 | 3.19–3.20 | 1.39 | 180 | 5.75 |
| Be-Bz-Be (c) | 0.20 | 1.72–2.83 | 1.37–1.52 | 135–140 | 3.29 |
| Be-Bz-Be (s) | 1.23 | 1.64–2.66 | 1.37–1.65 | 153 | 3.01 |
| Mg-Bz-Mg (p) | 0.21 | 3.46–3.48 | 1.39 | 180 | 6.36 |
| Ca-Bz-Ca (p) | 0.25 | 3.66–3.69 | 1.39 | 180 | 6.80 |
| Ca-Bz-Ca (c) | −0.05 | 2.53/3.55, 2.79/3.25 ⁑ | 1.37, 1.44 | 150 | 5.36 |
| Ca-Bz-Ca (s) | 0.12 | 2.61, 2.62 | 1.40, 1.50 | 180 | 4.38 |
| Sr-Bz-Sr (p) | 0.25 | 3.64–3.68 | 1.39 | 180 | 6.78 |
| Sr-Bz-Sr (c) | 0.05 | 2.69/3.52, 2.93/3.24 ⁑ | 1.37, 1.44 | 153 | 5.51 |
| Sr-Bz-Sr (s) | 0.28 | 2.75, 2.77 | 1.40, 1.50 | 180 | 4.73 |
| Ba-Bz-Ba (p) | 0.25 | 3.47 | 1.39 | 180 | 6.36 |
| Ba-Bz-Ba (s) | 1.40 | 2.89, 2.91 | 1.40, 1.50 | 180 | 5.05 |
| System | Q(M)/e | µ/D | HOMA | MCBO |
|---|---|---|---|---|
| Be-Bz (p) | −0.006 | 1.70 | 1.000 | 0.659 |
| Be-Bz (c) | 1.447 | 2.13 | −0.471 | 0.482 |
| Mg-Bz (p) | 0.0 | 1.95 | 1.000 | 0.659 |
| Ca-Bz (p) | 0.009 | 3.32 | 0.901 | 0.644 |
| Ca-Bz (c) | 0.776 | 1.28 | 0.138 | 0.581 |
| Sr-Bz (p) | 0.018 | 4.19 | 0.999 | 0.649 |
| Sr-Bz (c) | 0.925 | 1.67 | 0.461 | 0.586 |
| Ba-Bz (p) | 0.030 | 5.16 | 0.998 | 0.659 |
| Ba-Bz (c) | 1.487 | 4.98 | 0.310 | 0.557 |
| Be-Bz-Be (p) | 0.005 | 0.999 | 0.656 | |
| Be-Bz-Be (c) | 1.000, 0.850 | 1.83 | −0.572 | 0.425 |
| Be-Bz-Be (s) | 1.433 | 0.74 | −4.464 | −0.400 |
| Mg-Bz-Mg (p) | 0.0 | 0.999 | 0.661 | |
| Ca-Bz-Ca (p) | 0.005 | 0.999 | 0.635 | |
| Ca-Bz-Ca (c) | 0.951, 0.027 | 5.90 | 0.543 | 0.582 |
| Ca-Bz-Ca (s) | 0.951 | −0.178 | 0.347 | |
| Sr-Bz-Sr (p) | 0.008 | 0.998 | 0.635 | |
| Sr-Bz-Sr (c) | 0.994, 0.032 | 6.82 | 0.589 | 0.596 |
| Sr-Bz-Sr (s) | 0.942 | −0.058 | −0.349 | |
| Ba-Bz-Ba (p) | 0.019 | 0.995 | 0.642 | |
| Ba-Bz-Ba (s) | 0.915 | 0.136 | 0.259 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naumkin, F.Y. Main-Group Metal Complexes of Benzene: Predicted Features of Stabilization and Isomerization. Molecules 2023, 28, 5985. https://doi.org/10.3390/molecules28165985
Naumkin FY. Main-Group Metal Complexes of Benzene: Predicted Features of Stabilization and Isomerization. Molecules. 2023; 28(16):5985. https://doi.org/10.3390/molecules28165985
Chicago/Turabian StyleNaumkin, Fedor Y. 2023. "Main-Group Metal Complexes of Benzene: Predicted Features of Stabilization and Isomerization" Molecules 28, no. 16: 5985. https://doi.org/10.3390/molecules28165985
APA StyleNaumkin, F. Y. (2023). Main-Group Metal Complexes of Benzene: Predicted Features of Stabilization and Isomerization. Molecules, 28(16), 5985. https://doi.org/10.3390/molecules28165985