Systematic Theoretical Study on the pH-Dependent Absorption and Fluorescence Spectra of Flavins
Abstract
:1. Introduction
2. Computational Details
3. Results and Discussion
3.1. Absorption and Fluorescence Spectra of Flavins in Solution
3.2. Chemical Equilibrium of Flavins in Solution
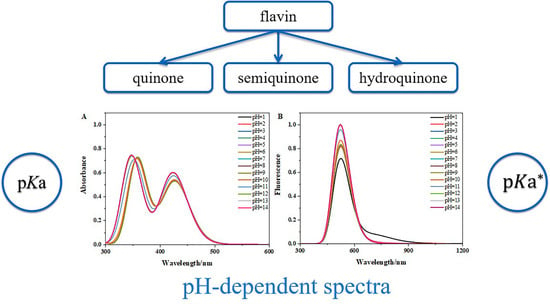
3.3. The pH-Dependent Absorption and Fluorescence Spectra of Flavins in Solution
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Huijbers, M.M.; Montersino, S.; Westphal, A.H.; Tischler, D.; van Berkel, W.J. Flavin Dependent Monoxygenases. Arch. Biochem. Biophys. 2014, 544, 2–17. [Google Scholar] [CrossRef] [PubMed]
- van Berkel, W.J.; Kamerbeek, N.M.; Fraaije, M.W. Flavoprotein Monooxygenases, A Diverse Class of Oxidative Biocatalysts. J. Biotechnol. 2006, 124, 670–689. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Koetter, J.W.A.; Schulz, G.E. Crystal Structure of 6-Hydroxy-d-nicotine Oxidase from Arthrobacter nicotinovorans. J. Mol. Biol. 2005, 352, 418–428. [Google Scholar] [CrossRef] [PubMed]
- Hassan-Abdallah, A.; Bruckner, R.C.; Zhao, G.; Jorns, M.S. Biosynthesis of Covalently Bound Flavin: Isolation and In vitro Flavinylation of the Monomeric Sarcosine Oxidase Apoprotein. Biochemistry 2005, 44, 6452–6462. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.-J. Understanding the Complete Bioluminescence Cycle from a Multiscale Computational Perspective: A review. J. Photochem. Photobiol. C 2022, 52, 1. [Google Scholar] [CrossRef]
- O’Kane, D.J.; Prasher, D.C. Evolutionary Origins of Bacterial Bioluminescence. Mol. Microbiol. 1992, 6, 443–449. [Google Scholar] [CrossRef]
- Mager, H.I.; Tu, S.C. Chemical Aspects of Bioluminescence. Photochem. Photobiol. 1995, 62, 607–614. [Google Scholar] [CrossRef]
- Colombo, B.; Saraceno, L.; Comi, G. Riboflavin and Migraine: The Bridge Over Troubled Mitochondria. Neurol. Sci. 2014, 35, 141–144. [Google Scholar] [CrossRef]
- Schulman, S.G. pH Dependence of Fluorescence of Riboflavin and Related Isoalloxazine Derivatives. J. Pharm. Sci. 1971, 60, 628–631. [Google Scholar] [CrossRef]
- Ahmad, I.; Anwar, Z.; Iqbal, K.; Ali, S.A.; Mirza, T.; Khurshid, A.; Khurshid, A.; Arsalan, A. Effect of Acetate and Carbonate buffers on the Photolysis of Riboflavin in Aqueous Solution: A Kinetic Study. AAPS PharmSciTech 2014, 15, 550–559. [Google Scholar] [CrossRef] [Green Version]
- Villabona-Monsalve, J.P.; Varnavski, O.; Palfey, B.A.; Goodson, T. Two-Photon Excitation of Flavins and Flavoproteins with Classical and Quantum Light. J. Am. Chem. Soc. 2018, 140, 14562–14566. [Google Scholar] [CrossRef] [PubMed]
- Ghisla, S.; Massey, V.; Lhoste, J.M.; Mayhew, S.G. Fluorescence and Optical Characteristics of Reduced Flavines and Flavoproteins. Biochemistry 1974, 13, 589. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Van den Berg, P.A.; Widengren, J.; Hink, M.A.; Rigler, R.; Visser, A.J. Fluorescence Correlation Spectroscopy of Flavins and Flavoenzymes: Photochemical and Photophysical Aspects. Spectrochim. Acta Part A 2001, 57, 2135–2144. [Google Scholar] [CrossRef]
- Ai, Y.; Zhao, C.; Xing, J.; Liu, Y.; Wang, Z.; Jin, J.; Xia, S.; Cui, G.; Wang, X. Excited-State Decay Pathways of Flavin Molecules in Five Redox Forms: The Role of Conical Intersections. J. Phys. Chem. A. 2018, 122, 7954–7961. [Google Scholar] [CrossRef] [PubMed]
- Tyagi, A.; Penzkofer, A. pH Dependence of the Absorption and Emission Behaviour of Lumiflavin in Aqueous Solution. J. Photochem. Photobiol. A 2010, 215, 108–117. [Google Scholar] [CrossRef]
- Song, S.H.; Dick, B.; Penzkofer, A.; Pokorny, R.; Batschauer, A.; Essen, L.O. Absorption and Fluorescence Spectroscopic Characterization of Cryptochrome 3 from Arabidopsis Thaliana. J. Photochem. Photobiol. B 2006, 85, 1–16. [Google Scholar] [CrossRef]
- Kabir, M.P.; Orozco-Gonzalez, Y.; Gozem, S. Electronic Spectra of Flavin in Different Redox and Protonation States: A Computational Perspective on the Effect of the Electrostatic Environment. Phys. Chem. Chem. Phys. 2019, 21, 16526–16537. [Google Scholar] [CrossRef]
- Schwinn, K.; Ferre, N.; Huix-Rotllant, M. UV-visible Absorption Spectrum of FAD and Its Reduced Forms Embedded in A Cryptochrome Protein. Phys. Chem. Chem. Phys. 2020, 22, 12447–12455. [Google Scholar] [CrossRef]
- Sato, K.; Nishina, Y.; Shiga, K. Decomposition of the Fluorescence Spectra of Two FAD Molecules in Electron-transferring Flavoprotein from Megasphaera elsdenii. J. Biochem. 2013, 154, 61–66. [Google Scholar] [CrossRef]
- Islam, M.S.; Honma, M.; Nakabayashi, T.; Kinjo, M.; Ohta, N. pH Dependence of the Fluorescence Lifetime of FAD in Solution and in Cells. Int. J. Mol. Sci. 2013, 14, 1952–1963. [Google Scholar] [CrossRef] [Green Version]
- Nakabayashi, T.; Islam, M.S.; Ohta, N. Fluorescence Decay Dynamics of Flavin Adenine Dinucleotide in a Mixture of Alcohol and Water in the Femtosecond and Nanosecond Time Range. J. Phys. Chem. B 2010, 114, 15254–15260. [Google Scholar] [CrossRef] [PubMed]
- Galban, J.; Sanz-Vicente, I.; Navarro, J.; de Marcos, S. The Intrinsic Fluorescence of FAD and Its Application in Analytical Chemistry: A Review. Methods Appl. Fluoresc. 2016, 4, 042005. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Su, D.; Kabir, M.P.; Orozco-Gonzalez, Y.; Gozem, S.; Gadda, G. Fluorescence Properties of Flavin Semiquinone Radicals in Nitronate Monooxygenase. Chembiochem 2019, 20, 1646–1652. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Tao, J.; Staroverov, V.N.; Scuseria, G.E.; Csonka, G.I. Prescription for the Design and Selection of Density Functional Approximations: More Constraint Satisfaction with Fewer Fits. J. Chem. Phys. 2005, 123, 062201. [Google Scholar] [CrossRef] [PubMed]
- Dreuw, A.; Head-Gordon, M. Single-reference ab Initio Methods for the Calculation of Excited States of Large Molecules. Chem. Rev. 2005, 105, 4009–4037. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate ab initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Runge, E.; Gross, E.K.U. Density-Functional Theory for Time-Dependent Systems. Phys. Rev. Lett. 1984, 52, 997–1000. [Google Scholar] [CrossRef]
- Ghisla, S.; Massey, V. New Flavins for Old: Artificial Flavins as Active Site Probes of Flavoproteins. Biochem. J. 1986, 1, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Kılıç, M.; Ensing, B. Acidity Constants of Lumiflavin from First Principles Molecular Dynamics Simulations. Phys. Chem. Chem. Phys. 2014, 16, 18993–19000. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Truhlar, D.G. The M06 suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, noncovalent Interactions, Excited states, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-class Functionals and 12 Other Functionals. Theor. Chem. Acc. 2007, 120, 215–241. [Google Scholar]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on A Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B. 2009, 113, 6378–6396. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Haber, F. Betrachtungen zur theorie der warmetonung. Ber. Dtsch. Phys. Ges. 1919, 21, 750. [Google Scholar]
- Liptak, M.D.; Shields, G.C. Accurate pK(a) Calculations for Carboxylic Acids Using Complete Basis Set and Gaussian-n Models Combined with CPCM Continuum Solvation Methods. J. Am. Chem. Soc. 2001, 123, 7314–7319. [Google Scholar] [CrossRef] [PubMed]
- Rashin, A.A.; Topol, I.A.; Tawa, G.J.; Burt, S.K. Charge Distributions in Water and Ion-water Clusters. Chem. Phys. Lett. 2001, 335, 327–333. [Google Scholar] [CrossRef]
- Kelly, C.P.; Cramer, C.J.; Truhlar, D.G. Aqueous Solvation Free Energies of Ions and Ion-water Clusters Based on An Accurate Value for the Absolute Aqueous Solvation Free Energy of the Proton. J. Phys. Chem. B 2006, 110, 16066–16081. [Google Scholar] [CrossRef] [Green Version]
- Houari, Y.; Jacquemin, D.; Laurent, A.D. Methodological Keys for Accurate pKa* Simulations. Phys. Chem. Chem. Phys. 2013, 15, 11875–11882. [Google Scholar] [CrossRef]
- Mondal, P.; Schwinn, K.; Huix-Rotllant, M. Impact of The Redox State of Flavin Chromophores on the UV–vis Spectra, Redox and Acidity Constants and Electron Affinities. J. Photochem. Photobiol. A 2020, 387, 1. [Google Scholar] [CrossRef]
- McBride, R.A.; Barnard, D.T.; Jacoby-Morris, K.; Harun-Or-Rashid, M.; Stanley, R.J. Reduced Flavin in Aqueous Solution Is Nonfluorescent. Biochemistry 2023, 62, 759–769. [Google Scholar] [CrossRef]
- Sakai, M. One-electron Photoreduction of Flavin Mononucleotide: Time-resolved Resonance Raman and Absorption Study. J. Mol. Struct. 1996, 379, 9–18. [Google Scholar] [CrossRef]
- Kar, R.K.; Miller, A.F.; Mroginski, M.A. Understanding Flavin Electronic Structure and Spectra. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2021, 12, 2. [Google Scholar] [CrossRef]
- Choe, Y.K.; Nagase, S.; Nishimoto, K. Theoretical Study of the Electronic Spectra of Oxidized and Reduced States of Lumiflavin and Its derivative. J. Comput. Chem. 2007, 28, 727–739. [Google Scholar] [CrossRef] [PubMed]
- Kar, R.K.; Borin, V.A.; Ding, Y.; Matysik, J.; Schapiro, I. Spectroscopic Properties of Lumiflavin: A Quantum Chemical Study. Photochem. Photobiol. 2019, 95, 662–674. [Google Scholar] [CrossRef] [PubMed]
- Brisker-Klaiman, D.; Dreuw, A. On the Influence of Dimerisation of Lumiflavin in Aqueous Solution on Its Optical Spectra—A Quantum Chemical Study. Mol. Phys. 2019, 117, 2167–2178. [Google Scholar] [CrossRef]
- Land, E.J.; Swallow, A.J. One-electron Reactions in Biochemical Systems as Studied by Pulse Radiolysis. II. Riboflavin. Biochemistry 1969, 5, 2117. [Google Scholar] [CrossRef]





| TD State Order | Transition | f | ||||
|---|---|---|---|---|---|---|
| This paper | 1 | 427.5 | 0.22 | 445.0 | ||
| Ref. [38] | 391.0 | 0.25 | ||||
| Ref. [17] | 1 | 422.7 | 0.24 | |||
| This paper | 2 | 358.7 | 0.31 | 370.0 | ||
| Ref. [38] | 326.0 | 0.26 | ||||
| Ref. [17] | 4 | 345.3 | 0.25 | |||
| This paper | 1 | 568.6 | 0.11 | 571.0 | ||
| Ref. [38] | 535.0 | 0.13 | ||||
| Ref. [17] | 1 | 581.0 | 0.13 | |||
| This paper | 2 | 460.3 | 0.06 | 485.0 | ||
| Ref. [38] | 406.0 | 0.06 | ||||
| Ref. [17] | 3 | 431.3 | 0.06 | |||
| This paper | 6 | 340.2 | 0.08 | 340.0 | ||
| Ref. [38] | 296.0 | 0.11 | ||||
| Ref. [17] | 5 | 360.3 | 0.09 | |||
| This paper | 2 | 450.8 | 0.04 | 480.0 | ||
| Ref. [38] | 423.0 | 0.13 | ||||
| Ref. [17] | 3 | 437.5 | 0.14 | |||
| This paper | 7 | 363.1 | 0.37 | 370.0 | ||
| Ref. [38] | 359.0 | 0.101 | ||||
| Ref. [17] | 6 | 357.6 | 0.297 | |||
| This paper | 1 | 392.4 | 0.06 | 395.0 | ||
| Ref. [38] | 400.0 | 0.03 | ||||
| Ref. [17] | 1 | 411.4 | 0.03 | |||
| This paper | 2 | 330.4 | 0.08 | 342.0 | ||
| Ref. [38] | 347.0 | 0.12 | ||||
| Ref. [17] | 2 | 345.4 | 0.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Liu, Y. Systematic Theoretical Study on the pH-Dependent Absorption and Fluorescence Spectra of Flavins. Molecules 2023, 28, 3315. https://doi.org/10.3390/molecules28083315
Wang J, Liu Y. Systematic Theoretical Study on the pH-Dependent Absorption and Fluorescence Spectra of Flavins. Molecules. 2023; 28(8):3315. https://doi.org/10.3390/molecules28083315
Chicago/Turabian StyleWang, Jinyu, and Yajun Liu. 2023. "Systematic Theoretical Study on the pH-Dependent Absorption and Fluorescence Spectra of Flavins" Molecules 28, no. 8: 3315. https://doi.org/10.3390/molecules28083315
APA StyleWang, J., & Liu, Y. (2023). Systematic Theoretical Study on the pH-Dependent Absorption and Fluorescence Spectra of Flavins. Molecules, 28(8), 3315. https://doi.org/10.3390/molecules28083315