Next Article in Journal
Biosynthesis of Silver Nanoparticles and Exploring Their Potential of Reducing the Contamination of the In Vitro Culture Media and Inducing the Callus Growth of Rumex nervosus Explants
Previous Article in Journal
New Indazol-Pyrimidine-Based Derivatives as Selective Anticancer Agents: Design, Synthesis, and In Silico Studies
Previous Article in Special Issue
Evolution of the Electronic Structure of the trans-[Re6S8bipy4Cl2] Octahedral Rhenium Cluster during Reduction
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 28
Issue 9
10.3390/molecules28093665
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Dimer Rhenium Tetrafluoride with a Triple Bond Re-Re: Structure, Bond Strength

by
Nina I. Giricheva
1,
Natalia V. Tverdova
2,
Valery V. Sliznev
2 and
Georgiy V. Girichev
2,*
1
Nanomaterial Research Institute, Ivanovo State University, Ermak Str. 39, 153025 Ivanovo, Russia
2
Department of Physics, Ivanovo State University of Chemistry and Technology, Sheremetevsky Ave. 7, 153000 Ivanovo, Russia
*
Author to whom correspondence should be addressed.
Molecules 2023, 28(9), 3665; https://doi.org/10.3390/molecules28093665
Submission received: 28 March 2023 / Revised: 20 April 2023 / Accepted: 21 April 2023 / Published: 23 April 2023
(This article belongs to the Special Issue DFT Quantum Chemical Calculation of Metal Clusters)
Browse Figures
Review Reports Versions Notes

Abstract

:
Based on the data of the gas electron diffraction/mass spectrometry (GED/MS) experiment, the composition of the vapor over rhenium tetrafluoride at T = 471 K was established, and it was found that species of the Re2F8 is present in the gas phase. The geometric structure of the Re2F8 molecule corresponding to D4h symmetry was found, and the following geometric parameters of the rh1 configuration were determined: rh1(Re-Re) = 2.264(5) Å, rh1(Re-F) = 1.846(4) Å, α(Re-Re-F) = 99.7(0.2)°, φ(F-Re-Re-F) = 2.4 (3.6)°. Calculations by the self-consistent field in full active space approximation showed that for Re2F8, the wave function of the 1A1g ground electronic state can be described by the single closed-shell determinant. For that reason, the DFT method was used for a structural study of Re2X8 molecules. The description of the nature of the Re-Re bond was performed in the framework of Atom in Molecules and Natural Bond Orbital analysis. The difference in the experimental values of r(Re-Re) in the free Re2F8 molecule and the [Re2F8]2− dianion in the crystal corresponds to the concept of a triple σ2π4 (ReIV-ReIV) bond and a quadruple σ2π4δ2 (ReIII-ReIII) bond, respectively, which are formed between rhenium atoms due to the interaction of d-atomic orbitals. The enthalpy of dissociation of the Re2F8 molecular form in two monomers ReF4 (ΔdissH°(298) = 109.9 kcal/mol) and the bond energies E(Re-Re) and E(Re-X) in the series Re2F8→Re2Cl8→Re2Br8 molecules were estimated. It is shown that the Re-Re bond energy weakly depends on the nature of the halogen, while the symmetry of the Re2Br8 (D4d) geometric configuration differs from the symmetry of the Re2F8 and Re2Cl8 (D4h) molecules.

Graphical Abstract

1. Introduction

There are various rhenium–rhenium bonded complexes, in which rhenium is in different oxidation states. Many experimental and theoretical works have been devoted to the consideration of such compounds [1,2,3,4,5,6]. The most common compounds with a rhenium–rhenium bond are compounds that contain a Re-Re quadruple bond, where the rhenium is in the +3 formal oxidation state (with the d4 configuration). This class of compounds stands out not only for its abundance but also for its historical significance.
The quadruple ReIII-ReIII bond in [Re2Cl8]2+ was the first of this kind to be observed; it opened up a new field of study in inorganic chemistry. It is believed that the bond between ReIII atoms can be represented as σ2π4δ2 [7,8,9,10,11,12]. The dianions [Re2X8]2− (where X = F, Cl, Br, I) have a very short Re-Re distance (2.19–2.25 Å) [7,8,9,10,11,12,13,14,15] and there is an eclipsed configuration of two ReF4 fragments relative to each other.
As noted in the literature, in contrast to their related compounds (ReIII, d4 configuration) with a lower degree of oxidation, ReIV (d3 configuration) complexes are not prone to the formation of metal–metal bonds [1]. Note that all experimental studies of the rhenium complexes structure refer to the condensed state.
In 1993, we performed gas electron diffraction/mass spectrometry (GED/MS) study of rhenium tetrafluoride vapor [16], which contains Re2F8 dimeric molecules, and determined the geometric structure of this molecular form. It was shown that the model of D4h symmetry with the Re-Re bond best fits the diffraction pattern. That is, the formation of a bond between the ReIV atoms was established. Due to the presence of a short distance r(Re-Re), the assumption of a Re-Re triple bond of σ2π4 type was made.
The question of what changes occur in the geometric and electronic structure of the [Re2X8]2− and Re2X8 complexes with ReIII-ReIII and ReIV-ReIV bonds is important for the structural chemistry of compounds with a metal–metal bond.
At present, the methodology for interpreting GED data has changed significantly. The modern GED experiment is a complex study, accompanied by a wide use of the results of quantum chemical calculations, which, along with determining the started geometry for a structural least square analysis of diffraction pattern, make it possible to describe the electronic structure of molecules.
For this, several theoretical methods for obtaining information about electronic properties and bond strength can be used. Population analysis methods such as the Natural Population Analysis (NPA) combined with the Natural Bond Orbital (NBO) method [17] as well as theoretical tools to analyze the topology of the electronic density of molecular systems such as Atom in Molecules (AIM) are among the most popular computational methods for analyzing electronic structures and bonding characters of complexes [18].
In this work, new technical and methodological improvements in the collection and interpretation of GED data were applied (see Section 4). Several density functional theory (DFT) approaches and NPA, NBO and AIM methods have been used to characterize the nature of the Re-Re bond and estimate the bond energies E(Re-Re) and E(Re-X) in the series of Re2F8 → Re2Cl8 → Re2Br8.
Comparison of the experimental structural parameters of Re2X8 molecules (ReIV-ReIV bond) and [Re2X8]2− dianions (ReIII-ReIII bond) with their calculated analogs makes it possible to recommend the most adequate calculation method for studying the properties of other complexes involving ReIII and ReIV.

2. Results

2.1. Analysis of GED/MS Data

The study of Re2F8 by the GED method could lead to serious errors if performed without mass spectrometric control of the gas phase composition. The rhenium tetrafluoride preparation was obtained by the reduction of ReF6 with metallic Re, and therefore, the sample could contain impurities of rhenium compounds in different oxidation states. The dynamics of changes in the mass spectrum at different temperatures confirms this assumption [16]. However, in the temperature range from 450 to 470 K, the relative intensity of ion currents in the mass spectrum over solid ReF4 practically does not change, the [ReF3]+(100), [ReF4]+(~50), [Re2F7]+(~50) ions, related to Re2F8, have the highest intensity, while the [ReF5]+ and [Re2F9]+ ions, which can have a Re2F10 molecular precursor, are only ~2 and ~1%, respectively. Thus, when analyzing the GED data (T = 471 K), one can use the assumption that the vapor contains a single Re2F8 molecular form.

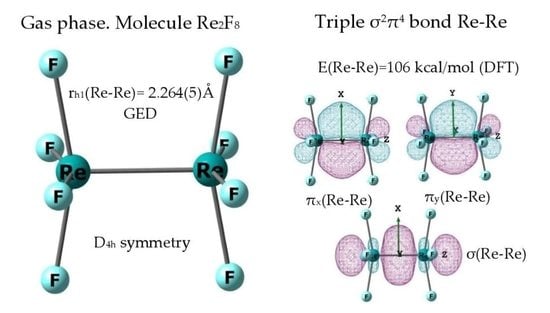
2.2. Geometric Structure of the Re2F8 Molecule

Before performing a structural analysis of the GED data, various models of the geometric structure of the Re2F8 molecule, presented in Figure 1, have been considered. DFT/PBE/RECP-3 theory level was used (the argumentation for choosing this variant and its designation is given in Section 4.2) when optimizing the geometry of each of the structures.
The D4h symmetry model (Figure 1a) has the minimum energy. The optimization of models with non-equivalent Re-F bonds of D2h (Figure 1c) and C2h (Figure 1e) symmetries leads to the same D4h structure. The model D2h with four Re-Fb bridging bonds (Figure 1d) is higher in energy than the D4h model (a) by ~100 kcal/mol. The energy of the D4d symmetry model (b) is only ~2.0 kcal/mol higher than that of the D4h model (a). Therefore, the parameters of the two models (a) and (b) were used as starting approximations in least squares (LS) analysis of the GED data.
Figure S1 shows the theoretical functions f(r) corresponding to models with the D4h and D4d symmetry of the Re2F8 molecule. These functions have significant differences in the region of 3–5 Å, indicating the possibility of determining the conformation of the molecule based on GED data.
As a result of the least-squares analysis of the electron diffraction data (details in Section 4.2), it was found that the Re2F8 molecule in the gas phase has an eclipsed D4h symmetry configuration, the parameters of which are given in Table 1.

2.3. GED Data and Frequency of Torsional Vibration of the Re2F8 Molecule

GED data were used to refine the frequency of torsional vibration νtors, which is less reliably determined in quantum chemical calculations, and more than other frequencies depends on the calculation theory level. The value of the torsion force constant significantly affects the amplitudes of vibrations of all F…F terms. Therefore, there is a fundamental possibility of determining νtors from GED data, especially since this vibration is characteristic and does not depend on other internal coordinates.
We have made an attempt to estimate νtors from its dependence on the disagreement factor between the experimental and theoretical functions of the reduced molecular scattering intensity Rf = f(νtors) (Table S1, details in Section 4.2). It turned out that the value of νtors = 30 cm−1 corresponds best to the GED experiment.
Figure 2 and Figure 3 show the experimental and theoretical functions sM(s) and f(r), which indicate that the geometric and vibrational characteristics of Re2F8 molecule with D4h symmetry (Table 1) are in agreement with the diffraction data.

2.4. Comparison of the Results of Two Methodology Approaches to LS-Analysis

Table 1 shows the rh1 obtained in this work and rα [16] structural parameters of the Re2F8 molecule. These parameters possess similar physical meaning but differ in the method of calculating vibrational corrections to the values of internuclear distances and root mean square vibrational amplitudes l (Table 1). Parameters of both rh1 and rα structures are approximations to the re parameters of the equilibrium configuration of the molecule. In [16], the harmonic approximation and linearized vibrational coordinates were used to calculate the vibrational amplitudes and vibrational corrections to the averaged internuclear distances. In this work, curvilinear vibrational coordinates were used. The latter technique allows obtaining rh1 parameters that are closer in physical meaning to the re parameters of the equilibrium configuration than rα parameters [19,20,21].
It can be seen that despite the different physical meaning, the rh1 and rα for the Re-Re bond are close. As for Re-F bond distance, a new obtained value is significantly close to the value predicted by PBE calculations (Table 1). It should be noted that the use of new methods of photometric experiment and a new approach to structural analysis (details in Section 4.2) allowed us to reduce the value of the disagreement factor Rf significantly (from 7% to 4.7%)
Thus, the previous GED study [16] of the Re2F8 molecule performed with an estimated force field gave the right conclusion concerning the symmetry of equilibrium configuration of this molecule without relying on quantum chemical calculations. However, the latter make it possible to significantly expand the understanding of the fine details of the geometric and electronic structure of molecules.

3. Discussion

3.1. The Nature of the Re-Re Chemical Bond in the Re2F8 Molecule

Saito [14] described in detail the ReIII-ReIII bond nature in the [Re2Cl8]2− dianion, which has a four multiplicity of σ2π4δ2 type. As noted in [14], one should expect that in a neutral Re2F8 molecule, the ReIV-ReIV bond will have the character of a σ2π4 triple bond. Our study confirms this assumption and develops ideas about the chemical bond in Re2F8.
The diagram of eight border canonical molecular orbitals (MO) and their view are shown in Figure 4. The dz2, dxz, dyz or dxy-AOs of two Re atoms make the main contribution to all noted MOs.
The dx2-y2 AOs are mainly involved in the formation of σ(Re-F) bonding and σ*(Re-F) antibonding MOs related to Re-F bonds of the Re2F8 molecule. They are in energy lower and higher MOs, as presented in Figure 4. The σ(Re-F) NBO and σ*(Re-F) NBO are shown in Figure 5.
If we neglect the contributions from the p-AO of fluorine atoms, then the MOs presented in Figure 4 can be classified as follows: the a1g symmetry orbital represents the occupied bonding σ(Re-Re) MO built from dz2 AOs; two occupied orbitals of eu symmetry represent degenerate bonding MOs πx(Re-Re) and πy(Re-Re) built from dxz or dyz AOs; the unoccupied b2g orbital refers to the bonding δ(Re-Re) MO, consisting of dxy AOs; orbitals of symmetry b1u, eg, and a2u refer to antibonding δ*(Re-Re), πx*(Re-Re) = πy*(Re-Re) and σ*(Re-Re) MOs, respectively. The electronic configuration a1g2eu4 corresponds to a σ2π4 triple bond between rhenium atoms.
The results of AIM and NBO analysis (Table 2), despite the difference in approaches to the analysis of the electronic structure of the molecule, demonstrate agreement in the values of bond orders (δAIM/PNBO), which are more than two for the Re-Re bond and close to 1 for the Re-F bonds. The bond ellipticity (ε) of the Re-Re is equal to 0, which confirms the σ2π4 character of this bond. The net charges on the Re and F atoms indicate a noticeable ionic component of the Re-F bond.

3.2. Free Re2F8 Molecule in the Gas Phase and [Re2F8]2− Dianion in Crystals; the ReIV-ReIV Bond vs. the ReIII-ReIII Bond

In [Re2X8]2− dianions with D4h symmetry, the molecular orbital δ(b2g) of the Re-Re bond becomes the highest occupied molecular orbital (HOMO), the δ*(b1u) orbital is the lowest unoccupied molecular orbital (LUMO) (Figure 4), and the difference between the energies of the frontier orbitals is much smaller than between frontier orbitals in Re2X8 molecules (X = Hal). Therefore, the methods of quantum chemical calculations for the Re2X8 molecule and the [Re2X8]2− dianion are fundamentally different ([14] and Section 4.1).
Nevertheless, it is possible to compare the geometric and vibrational parameters of the molecules and the dianions calculated using the DFT because this approximation reliably predicts the structure of the mentioned species (Table S2).
Table 3 shows the experimental internuclear distances and the calculated frequencies of ν(Re-Re) stretching vibration and νtors torsion vibration as well as NPA charges on atoms in two species Re2F8 and [Re2F8]2−.
Both species have an eclipsed D4h geometric configuration with 1A1g ground state symmetry, the electronic configurations of which correspond to the triple σ2π4 and quadruple σ2π4δ2 Re-Re bonds, respectively. Those Re-Re bond should become shorter, and the frequency of the ν(Re-Re) stretching vibration should be higher when going from Re2F8 to [Re2F8]2−.
The NPA charges on the F atoms in Re2F8 and [Re2F8]2− indicate an increase in the energy of steric repulsion between them in the dianion, which leads to the lengthening of all F…F distances and an increase in the bond angle FReRe. At the same time, a larger difference between the charges on the Re and F atoms can be one of the factors for the shortening of the Re-F distance in the Re2F8 molecule.
In addition, both in the molecule and in the dianion, there are donor–acceptor interactions between the bonding σ(Re1-F) NBO of one ReF4 fragment and the antibonding σ*(Re2-F) NBO of another ReF4 fragment (Figure 5).
As a result of such interactions, the electron density is transferring from the bonding NBO to the antibonding one. This circumstance leads to a weakening of both the Re1-F bond and the Re2-F bond. Since the energy of this interaction in the dianion is almost two times greater than in the molecule, the distance r (Re-F) in the dianion is longer, and the frequency of the stretching vibration ν (Re-F) is lower.
This is evidenced by the bond orders calculated according to the Weiberg scheme [17]: P (Re-Re) = 2.24 and 3.10, P (Re-F) = 0.81 and 0.59 for Re2F8 and [Re2F8]2−, respectively.
The presence of the δ (Re-Re) bond, as well as the presence of such strong donor–acceptor interactions that prevent internal rotation, can explain the greater value of the torsional vibration frequency in the dianion.

3.3. Structural Changes in the Series Re2F8 → Re2Cl8 → Re2Br8

This section presents the results of calculations for Re2Cl8 and Re2Br8 molecules. Experimental data on their structure are absent in the literature. The same variant of the DFT method was used, which led to better agreement between the calculated and experimental parameters of the Re2F8 molecule (Section 4.2). Moreover, the calculated structural characteristics of the [Re2X8]2− dianions of these compounds coincided within the error limit with the experimental data found by X-ray diffraction analysis [9,10,11,12,13] (Table S2).
Some molecular characteristics of the three Re2X8 molecules are given in Table 4, allowing to trace the influence of the nature of the atom halogen X on their structure. Thus, r (Re-Re) increases by ~0.08 Å during the transition Re2F8 → Re2Cl8 → Re2Br8 (D4h), while in the dianion series, this increase is noticeably weaker (~0.04 Å, Table S2), which is due to the stronger and shorter Re-Re bond in dianions.
With the lengthening of the Re-Re bond, the frequency of the ν (Re-Re) stretching vibration decreases as expected (Table 4). The Re-Re-X and X-Re-X bond angles change by no more than 3°, and they are close to 90°, which indicates a significant contribution of 5dx2-y2 AO of rhenium atoms to the formation of Re-X bonds.
The distances r (X…X) between halogen atoms in the cis position with respect to each other are less than the sum of their van der Waals radii, and the difference between r (X…X) and ΣrVdV (X) increases when going from F to Br. This leads to an increase in steric repulsion between ReX4 fragments in Re2X8 molecules.

3.4. D4h or D4d Symmetry of Re2X8 Molecules?

It was noted in [14] that in contrast to [Re2X8]2− dianions with a quadruple σ2π4δ2 Re-Re bond, in the neutral form Re2X8, the free internal rotation of ReX4 groups around the σ2π4 triple bond, which has axial symmetry, is possible.
It is assumed [14] that when the symmetry of the molecule is lowered from D4h to D4d, the steric repulsion energy between X atoms of two ReX4 groups will decrease, which will make the D4d configuration of Re2X8 molecules more energetically favorable than D4h.
However, as noted in Section 2.2, the GED data indicate the D4h symmetry of the geometric configuration of the Re2F8 molecule. To confirm this conclusion, we scanned the potential energy surface along the torsion coordinate F-Re-Re-F. The calculation of the total energy at each point in Figure 6 was carried out at a fixed value of the dihedral angle φ (F-Re-Re-F) by optimizing all other geometric parameters while maintaining the D4 symmetry.
The analysis of molecular orbitals carried out for all points on the internal rotation function (Figure 6) showed that the shape and composition of the molecular orbitals responsible for the formation of the Re-Re triple bond remain practically unchanged. Apparently, the constancy of the electron density distribution in the region of the Re-Re bond is the reason for the low barrier of internal rotation with respect to the triple bond.
The PFIR (Figure 6) indicates that the D4h symmetry model is a stable Re2F8 structure, and the geometry of D4d symmetry corresponds to a first-order saddle point, where the imaginary frequency refers to the torsional vibration. It can be seen that the barrier of internal rotation is ~2 kcal/mol, and it significantly exceeds the thermal energy RT (~0.94 kcal/mol), which corresponds to the temperature of the GED experiment and the change in the torsion angle ϕ (F-Re-Re-F) = 0 ± 21°. In this case, the vibration amplitude of the F5…F10 term is equal to 0.325 Å, and it corresponds to the experimental value from GED (Table 1).
For the Re2Cl8 molecule, the barrier value decreases (to 1.1 kcal/mol), as well as the value of νtors (Re-Re), which indicates a greater structural non-rigidity of Re2Cl8 compared to the Re2F8 molecule.
At last, for the Re2Br8 molecule, the D4d symmetry configuration becomes more stable compared to D4h (Table 4), which becomes the first-order saddle point on the potential energy surface (PES). Such a change in the energy difference E(D4d) − E(D4h) in the series Re2F8 → Re2Cl8 → Re2Br8 corresponds to an increase in the steric repulsion energy between halogen atoms because of small changes in the Re-Re bond length and the Re-Re-X bond angle and an increase in the effective size of halogens.

3.5. Re2F8 Dissociation Enthalpy and Re-Re and Re-X Bond Energy in Re2X8 Molecules

The enthalpy of dissociation of Re2F8 was estimated in [22] basing the experimental values of the standard enthalpies of formation of gaseous and solid rhenium tetrafluoride and the enthalpy of Re2F8 sublimation. The value ΔdissH° (298) was estimated as 112 ± 16 kcal/mol. To verify this value, we have considered the gas-phase dissociation reaction
Re2F8 → 2∙ReF4
using the PBE/RECP-3 method (see Section 4.2).
For this, geometric optimization of the ReF4 molecule (q = 0) with a multiplicity (M) of electronic state equal to 4 was performed, which implies the presence of three unpaired electrons. According to the crystal field theory, the initial ReF4 tetrahedral configuration must undergo Jahn–Teller distortions and reduce the symmetry to D2d. The calculation results confirm this.
NBO analysis shows that three unpaired electrons are located on 5dxy, 5dx2-y2, and 5dz2 AOs, resulting in a distorted tetrahedral structure extended along the x-axis (Figure 7).
The energy of the Re2F8 dissociation reaction was calculated by Equation (1) as the difference between the electronic energies of the Re2F8 and ReF4 molecules:
ΔEdiss = 2·E[ReF4 (D2d)] − E[Re2F8 (D4h)]
and amounted to ΔEdiss = 111.68 kcal/mol.
The enthalpy and Gibbs free energy of dissociation were calculated in a similar way:
ΔdissH° (298) = 109.9 kcal/mol
ΔdissG° (298) = 93.2 kcal/mol
Note that the calculated value of ΔdissH (298) coincides with the value [22] estimated from experimental thermochemical data (112 ± 16 kcal/mol).
For Re2F8, Re2Cl8, and Re2Br8 molecules, the Re-Re bond energy was estimated taking into account the basis set superposition error (BSSE) [23,24]. It was assumed that the original Re2X8 molecule consists of two ReX4 fragments (q = 0, M = 4). The BSSE correction turned out to be small (~1 kcal/mol).
The Re-X bond energy was estimated according to Equation (2):
E(Re-X) = E(Re2X7∙) + E(F) − E(Re2X8)
where E(Re2X7∙) is the electronic energy of the radical Re2X7 ∙ (M = 2) with its geometry in the Re2X8 molecule, and E(F∙) is the electronic energy of the F atom (M = 2).
The Re-Re and Re-X bond energies in Re2F8, Re2Cl8 and Re2Br8 molecules are given in Table 4. As can be seen, the energies E(Re-Re) change slightly when replacing halogens. There is a close to linear correlation between the calculated Re-X bond energy and the internuclear distance r(Re-X) (Figure 8.).

4. Materials and Methods

4.1. Details of Calculations

Most of the quantum chemical calculations in this work were performed by the DFT method. The argument for using DFT was the results of calculations of the total energies of singlet and triplet electronic states by the self-consistent field in the full active space (CASSCF) method, which was followed by taking into account the dynamic correlation of electrons in the framework of the multiconfiguration, quasi-degenerate second-order perturbation theory (MCQDPT2) [25,26] for the Re2F8 molecule using the FireFly 8.2 program [27].
In this case, geometric parameters obtained by optimization in the DFT/PBE0 approximation were used.
The active space of the CASSCF method included 6 electrons and 10 molecular orbitals, consisting mainly of a combination of the corresponding components of the 5d orbitals of two rhenium atoms. Calculations in the CASSCF approximation performed for the singlet states of the equilibrium D4h symmetry configuration of the Re2F8 molecule showed that the weight of the leading Slater determinant in the wave function of the ground singlet electronic state (1A1g) is 86%.
The relative energy of the nearest excited singlet state is 127 kcal/mol. Calculations of the total energies of triplet electronic states performed in the CASSCF and MCQDPT2 approximations showed that the lower triplet term (3Eu) lies above the ground singlet electronic state by 57 and 23 kcal/mol, respectively.
The leading determinant in the wave function of the ground electronic state 1A1g corresponds to the closed-shell electron configuration, which was implemented in DFT calculations.
DFT calculations were performed with three functional/basis combinations and different pseudopotentials of the Re atom. The calculated geometric parameters of the Re2F8 molecule, obtained in three versions, are compared with the experimental data in Table 5.
Calculations in the PBE0 approximation [28] were performed using the FireFly 8.2 software [27]. The quasi-relativistic effective pseudopotential (qRECP) and correlation consistent basis set [29] was used for the Re atom. For the fluorine atom, the Sapporo basis (SPKrATZP) [30,31] supplemented with diffuse functions was applied (referred to as PBE0/qRECP-1).
Calculations with the B3LYP [32,33,34] and PBE [35] functionals were performed using the Gaussian09 program [36].
In the DFT/B3LYP calculation, the quasi-relativistic effective core potentials [29] and the basis set [37] on the Re atom was used. Fluorine atoms were described using the correlation-consistent valence-three-exponential cc-pVTZ basis set [38] (referred to as B3LYP/qRECP-2).
In the DFT/PBE approximation, the relativistic effective pseudopotentials (RECP) and the corresponding aug-cc-pVTZ-PP basis set [39] was used to describe the rhenium atom. The basis set aug-cc-pVTZ was applied to describe fluorine [38,40], chlorine [41], and bromine [42] atoms (referred to as PBE/RECP-3).
Effective core potentials and basis sets in the Gaussian program format were adopted from the Basis Set Exchange library (BSE) [43,44,45].
For the ground electronic states, the topological analysis of electron density distribution function ρ(r) for the molecules under study was carried out using AIMAll Professional software [18]. The NBO 5G program [17], implemented for natural orbital analysis in FireFly 8.2 [27], was used to obtain the net atomic charges, and to study the effect of hyperconjugation on the structure. Visualization of the geometrical structures and orbitals was performed by the ChemCraft program [46].

4.2. Features of Structural Analysis of GED/MS Data

The gas phase electron diffraction patterns and mass spectra were recorded simultaneously using the technique described in ref. [47,48]. The conditions of the synchronous gas-phase electron diffraction/mass spectrometric (GED/MS) experiments are shown in Table S3. The optical densities of exposed photoplates were recorded for two nozzle-to-plate distances: L1 = 598 mm and L2 = 338 mm. Seven electron diffraction patterns of the substance and two electron diffraction patterns of the ZnO crystal standard were recorded for each nozzle-to-plate distance.
In Ref. [16], electron diffraction patterns were scanned by their diameter. As a result, the diffraction pattern for each photographic plate was represented by a set of 301 points. In this case, the complete statistical sample for all electron diffraction patterns was 4214 points.
In contrast to [16], we increased significantly the sample of scanning results and precision of optical density measurements. To achieve this goal, we used a modified MD-100 microdensitometer [49] and measured the optical density on each plate by scanning an area of 10 × 130 mm with a step of 0.1 mm along 33 equidistant scanning lines. As a result of new microphotometric measurements, the statistical sample of primary experimental data was significantly increased in comparison with [16] and amounted to more than 500,000 points.
The geometric model of the Re2F8 molecule was specified by four independent parameters: two internuclear distances Re-Re, Re-F, bond angle FReRe and dihedral angle FreReF. The values of dependent internuclear distances were determined within the framework of the rh1 structure. The independent parameters together with five groups of root-mean-square vibration amplitudes were varied during the least-squares analysis of GED data using the modified KCED-35 program [50].
The VibModule program [51] was applied to calculate the vibrational corrections Δr = rh1 − ra and the starting values of root-mean-square vibration amplitudes of Re2F8 at the temperature of the GED experiment using the harmonic approximation and taking into account the non-linear interrelation between internal and Cartesian vibrational coordinates.
The DFT method with three different functionals and basis sets (see Section 4.1) was used to calculate the starting molecular characteristics of the Re2F8 molecule (Table 5). The LS analysis of GED data showed that three variants of starting parameters lead to identical geometric and vibrational parameters of the experimental structure, which indicates the stability of the solution of the GED inverse task.
Table 5 shows the geometrical parameters of the D4h symmetry structure, the frequency of stretching vibrations ν(Re-Re) and stretching vibrations ν(Re-F), as well as the torsional vibration νtors(Re-Re), which are calculated in three functionals of DFT for the Re2F8 molecule.
Comparison of the calculated parameters with the experimental ones (Table 5) shows that the PBE/RECP-3 combination has an advantage over other calculation variants and may be used to estimate the geometric structure of the Re2X8 molecules as well as of the [Re2X8]2− dianions.
Table S4 and Figure S2 show the vibrational frequency values of the molecule Re2F8 obtained in three variants using DFT. Differences in the values of the Re-F stretching vibration frequencies (590–750 cm−1) and the F-Re-F and Re-Re-F bending vibrations (125–750 cm−1) lead to changes in vibrational amplitudes of terms F…F, which do not exceed the error of their determination in the GED experiment, when using the same value of the torsion vibration frequency. At the same time, as noted in Section 2.3, the value of the torsion force constant significantly affects the vibrational amplitudes of all terms F…F.
To determine the value of the νtors, the different torsion force constants were used for the calculation of starting values of the vibrational amplitudes by the VibModule program [51], which were then refined in the LS analysis of the GED data (Table S1). It turned out that at νtors = 30 cm−1, the value of the disagreement factor Rf between the experimental and theoretical functions sM(s) acquires a minimum value, and the calculated amplitude F5…F10 coincides with the experimental one.
As a result of the applied and described above improvements in the quality of photometric measurements and the use of quantum chemical calculations for obtaining the force field of a molecule and an improved method for calculating the vibrational characteristics of a molecule [19,20,21], it was possible to achieve a significantly better agreement between the model scattering intensity function and experiment (R = 4.7% versus 7.0% in [16]).

5. Conclusions

The reinterpretation of the diffraction data [16] for gaseous rhenium tetrafluoride has been carried out at a higher methodological level. In the temperature range from 450 to 470 K, the dominant species of the vapor is Re2F8. The Re2F8 molecule possesses a geometric structure of D4h symmetry. Based on the GED data, the frequency of torsional vibrations relative to the Re-Re bond, which is associated with the structural non-rigidity of the molecule, was estimated.
The electronic structure of Re2F8 was determined in the CASSCF and MCQDPT2 approximations, and it was shown that the 1A1g ground electronic state can be described by a single-reference wave function. This circumstance indicates the possibility of using the DFT method for extended analysis of the geometric and electronic structure of molecules in the series Re2F8 → Re2Cl8 → Re2Br8.
The potential function of the internal rotation of ReF4 fragments relative to the Re-Re bond of the Re2F8 molecule has been calculated. Structural changes in the series Re2F8 → Re2Cl8 → Re2Br8 free molecules were considered. The transition from fluoride to chloride leads to a decrease in the barrier V = E(D4d) − E(D4h), and for Re2Br8, the D4h symmetry structure becomes a saddle point on the PES. This fact does not contradict the concept of an increase in the steric repulsion between ReX4 fragments with an increase in the effective size of the X halogen atom. The heat of dissociation of the Re2F8 species (ΔdissH°(298) = 109.9 kcal/mol). The bond energies E(Re-Re) and E(Re-X) in the series Re2F8 → Re2Cl8 → Re2Br8 molecules were estimated.
The results of the NBO analysis and QTAIM, despite the difference in approaches to the analysis of the electronic structure of the molecule Re2F8, demonstrate agreement in the values of bond orders, which are more than 2 for the Re-Re bond and close to 1 for the Re-F bond. The ellipticity of the Re-Re bond is equal to 0 and confirms the σ2π4 character of this bond. The net charges on the Re and F atoms indicate a noticeable ionic component of the Re-F bond. Structural features of free Re2F8 molecule in the gas phase and [Re2F8]2− dianion in crystals are considered.
There is a shortening of the Re-Re bond and an increase in the ReReF bond angle upon passing from Re2F8 to [Re2F8]2−, and this fact corresponds to the concept of a triple σ2π4 (ReIV-ReIV) bond and a quadruple σ2π4δ2 (ReIII-ReIII) bond, which are formed between rhenium atoms due to the interaction of d AOs in individual molecules and in ion fragments of crystal, correspondingly.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules28093665/s1, Figure S1. Theoretical functions f(r) for models D4h and D4d of the Re2F8 molecule and difference curve Δf(r); Figure S2. Values of 24 vibrational frequencies of the Re2F8 molecule, calculated with three versions of the DFT method: Table S1. Disagreement factor Rf and calculated vibration amplitude l(F5…F10) versus the torsion vibration frequency of the Re2F8 molecule; Table S2. Calculated and experimental structural characteristics of the [Re2X8]2− (X = F, Cl, Br); Table S3. Conditions of the synchronous GED/MS experiments; Table S4. The vibrational frequency values of the molecule Re2F8 obtained in three variants of DFT.

Author Contributions

Conceptualization, G.V.G. and N.I.G.; methodology, G.V.G. and N.I.G.; investigation: N.I.G., N.V.T., V.V.S. and G.V.G.; formal analysis, N.V.T., N.I.G. and V.V.S., resources, N.I.G. and G.V.G.; writing—original draft preparation, N.I.G., N.V.T. and V.V.S.; writing—review and editing, G.V.G.; visualization, N.V.T. and N.I.G.; supervision, G.V.G.; project administration, G.V.G.; funding acquisition, G.V.G. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Russian Science Foundation (grant No 20-13-00359).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Acknowledgments

N.I.G. thanks the Russian Ministry of Science and High Education for support of quantum chemical calculation and the structural analysis of electron diffraction data (grant No FZZM-2023-0009). The gas-phase electron diffraction/mass-spectrometric experiments were carried out using the GED/MS equipment (https://www.isuct.ru/department/ckp/structure/ged-ms, (accessed on 20 March 2023) of the resources of the Center for Shared Use of Scientific Equipment of the ISUCT (with the support of the Ministry of Science and Higher Education of Russia, grant No. 075-15-2021-671).

Conflicts of Interest

The authors declare no conflict of interest.

Sample Availability

Samples of the compounds are not available from the authors.

References

  1. Sasaki, Y. Recent Progress in the Chemistry of Rhenium Cluster Complexes and Its Relevance to the Prospect of Corresponding Technetium Chemistry. J. Nucl. Radiochem. Sci. 2005, 6, 145–148. [Google Scholar] [CrossRef] [PubMed]
  2. Valdés, D.H.; Alberto, R.; Jáuregui-Haza, U. Quantum chemistry calculations of technetium and rhenium compounds with application in radiopharmacy: Review. RSC Adv. 2016, 6, 107127–107140. [Google Scholar] [CrossRef]
  3. Demoin, D.W.; Li, Y.; Jurisson, S.S.; Deakyne, C.A. Method and basis set analysis of oxorhenium(V) complexes for theoretical calculations. Comp. Theor. Chem. 2012, 997, 34–41. [Google Scholar] [CrossRef]
  4. Li, Y.; Ma, L.; Gaddam, V.; Gallazzi, F.; Hennkens, H.M.; Harmata, M.; Lewis, M.R.; Deakyne, C.A.; Jurisson, S.S. Synthesis, Characterization, and In Vitro Evaluation of New 99mTc/Re(V)-Cyclized Octreotide Analogues: An Experimental and Computational Approach. Inorg. Chem. 2016, 55, 1124–1133. [Google Scholar] [CrossRef] [PubMed]
  5. Noor, A.; Huff, G.S.; Kumar, S.V.; Lewis, J.E.M.; Paterson, B.M.; Schieber, C.; Donnelly, P.S.; Brooks, H.J.L.; Gordon, K.C.; Moratti, S.C.; et al. [Re(CO)3]+ Complexes of exo-Functionalized Tridentate “Click” Macrocycles: Synthesis, Stability, Photophysical Properties, Bioconjugation, and Antibacterial Activity. Organometallics 2014, 33, 7031–7043. [Google Scholar] [CrossRef]
  6. Hernández-Valdés, D.; Rodríguez-Riera, Z.; Díaz-García, A.; Benoist, E.; Jáuregui-Haza, U. Influence of the chelator structures on the stability of Re and Tc tricarbonyl complexes with iminodiacetic acid tridentate ligands: A computational study. J. Mol. Model. 2016, 22, 179. [Google Scholar] [CrossRef]
  7. Cotton, F.A.; Harris, C.B. The Crystal and Molecular Structure of Dipotassium Qctachlorodirhenate(III) Dihydrate, K2[Re2Cl8]·2H2O. Inorg. Chem. 1965, 4, 330–333. [Google Scholar] [CrossRef]
  8. Cotton, F.A.; DeBoer, B.G.; Jeremic, M. Some Reactions of the Octahalodirhenate(III) Ions. Definitive Structural Characterization of the Octabromodirhenate(III) Ion. Inorg. Chem. 1970, 9, 2143–2146. [Google Scholar] [CrossRef]
  9. Cotton, F.A.; Frenz, B.A.; Stults, B.R.; Webb, T.R. Investigations of Quadruple Bonds by Polarized Crystal Spectra. I. The Interpretation of the Spectrum of Tetra(n-butylammonium) Octachlorodirhenate. The Disordered Crystal Structure. J. Am. Chem. Soc. 1976, 98, 2768–2773. [Google Scholar] [CrossRef]
  10. Cotton, F.A.; Hall, W.T. Cesium Octachlorodirhenate(II1) Hydrate. The Correct Structure and Its Significance with Respect to the Nature of Metal-Metal Multiple Bonding. Inorg. Chem. 1977, 16, 1867–1871. [Google Scholar] [CrossRef]
  11. Huang, H.W.; Martin, D.S. Single-crystal polarized spectra for the .delta. .fwdarw. .delta.* band of tetrabutylammonium octachlorodirhenate(III) and tetrabutylammonium octabromodihenate(III). Crystal structure of the octabromo salt. Inorg. Chem. 1985, 24, 96–101. [Google Scholar] [CrossRef]
  12. Conradson, S.D.; Sattelberger, A.P.; Woodruff, W.H. X-ray Absorption Study of Octafluorodirhenate(III): EXAFS Structures and Resonance Raman Spectroscopy of Octahalodirhenates. J. Am. Chem. Soc. 1988, 110, 1309–1311. [Google Scholar] [CrossRef]
  13. Cotton, F.A.; Daniels, L.M.; Vidyasagar, K. The crystal structure of [(n-C4H9)4N]2Re2I8: Three-fold disorder of the effectively cubic anion. Polyhedron 1988, 7, 1667–1672. [Google Scholar] [CrossRef]
  14. Saito, K. Theoretical Studies on Electronic Excited States of Transition Metal Complexes: Explanation and Understanding Based on Molecular Geometries and Electronic Structures. Ph.D. Thesis, Kyoto University, Kyoto, Japan, 2012; pp. 1–152. [Google Scholar] [CrossRef]
  15. Henkel, G.; Peters, G.; Preetz, W.; Skowronek, J. Kristallstruktur und Schwingungsspektren von [(n-C4H9)4N]2[Re2F8]·2(C2H5)2O. Z. Naturforsch. B 1990, 45, 469–475. [Google Scholar] [CrossRef]
  16. Giricheva, N.I.; Girichev, G.V.; Lapshina, S.B.; Shlykov, S.A.; Politov, Y.A.; Butskii, V.D.; Pervov, V.S. Geometric structure and vibration frequencies of Re2F8. J. Struct. Chem. 1993, 34, 214–224. [Google Scholar] [CrossRef]
  17. Glendening, E.D.; Badenhoop, J.K.; Reed, A.E.; Carpenter, J.E.; Bohmann, J.A.; Morales, C.M.; Weinhold, F. NBO 5.G. 2004. Available online: http://www.chem.wisc.edu/~nbo5 (accessed on 20 March 2023).
  18. Keith, T.A. AIMAll; TK Gristmill Software: Overland Park, KS, USA, 2016. [Google Scholar]
  19. Sipachev, V.A. Calculation of shrinkage corrections in harmonic approximation. J. Mol. Struct. (Theochem.) 1985, 121, 143–151. [Google Scholar] [CrossRef]
  20. Sipachev, V.A. Vibrational effects in diffraction and microwave experiments: A start on the problem. In Advances in Molecular Structure Research; Hargittai, I., Hargittai, M., Eds.; JAI Press: New York, NY, USA, 1999; pp. 263–311. [Google Scholar]
  21. Sipachev, V.A. Local centrifugal distortions caused by internal motions of molecules. J. Mol. Struct. 2001, 67–72, 567–568. [Google Scholar] [CrossRef]
  22. Politov, Y.A.; Alikhanjan, A.S.; Butskiy, V.D.; Pervov, V.S.; Buslaev, Y.A. Polimeric molecules of lower rhenium fluorides. Proc. USSR Acad. Sci. 1987, 296, 1385–1387. (In Russian) [Google Scholar]
  23. Boys, S.F.; Bernardi, F. Calculation of Small Molecular Interactions by Differences of Separate Total Energies—Some Procedures with Reduced Errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
  24. Simon, S.; Duran, M.; Dannenberg, J.J. How does basis set superposition error change the potential surfaces for hydrogen bonded dimers? J. Chem. Phys. 1996, 105, 11024–11031. [Google Scholar] [CrossRef]
  25. Nakano, H. Quasidegenerate perturbation theory with multiconfigurational self-consistent-field reference functions. J. Chem. Phys. 1993, 99, 7983–7992. [Google Scholar] [CrossRef]
  26. Witek, H.A.; Choe, Y.-K.; Finley, J.P.; Hirao, K. Intruder state avoidance multireference Møller–Plesset perturbation theory. J. Comput. Chem. 2002, 23, 957–965. [Google Scholar] [CrossRef] [PubMed]
  27. Granovsky, A.A. Firefly. Version 8. 2013. Available online: http://classic.chem.msu.su/gran/firefly/index.html (accessed on 20 March 2023).
  28. Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6169. [Google Scholar] [CrossRef]
  29. Andrae, D.; Häußermann, U.; Dolg, M.; Stoll, H.; Preuß, H. Energy-adjusted ab initio pseudopotentials for the second and third row transition elements. Theor. Chim. Acta 1990, 77, 123–141. [Google Scholar] [CrossRef]
  30. Tatewaki, H.; Koga, T. Contracted Gaussian-type basis functions revisited. J. Chem. Phys. 1996, 104, 8493–8499. [Google Scholar] [CrossRef]
  31. Noro, T.; Sekiya, M.; Koga, T. Contracted polarization functions for the atoms helium through neon. Theor. Chem. Acc. 1997, 98, 25–32. [Google Scholar] [CrossRef]
  32. Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5653. [Google Scholar] [CrossRef]
  33. Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3101. [Google Scholar] [CrossRef]
  34. Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
  35. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868, Erratum in Phys. Rev. Lett. 1997, 78, 1396. [Google Scholar] [CrossRef]
  36. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Version D.02; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
  37. Martin, J.M.L.; Sundermann, A. Correlation consistent valence basis sets for use with the Stuttgart–Dresden–Bonn relativistic effective core potentials: The atoms Ga–Kr and In–Xe. J. Chem. Phys. 2001, 114, 3408–3420. [Google Scholar] [CrossRef]
  38. Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
  39. Figgen, D.; Peterson, K.A.; Dolg, M.; Stoll, H. Energy-consistent pseudopotentials and correlation consistent basis sets for the 5d elements Hf-Pt. J. Chem. Phys. 2009, 130, 164108. [Google Scholar] [CrossRef]
  40. Kendall, R.A.; Dunning, T.H.; Harrison, R.J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef]
  41. Woon, D.E.; Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon. J. Chem. Phys. 1993, 98, 1358–1371. [Google Scholar] [CrossRef]
  42. Wilson, A.K.; Woon, D.E.; Peterson, K.A.; Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. IX. The atoms gallium through krypton. J. Chem. Phys. 1999, 110, 7667–7676. [Google Scholar] [CrossRef]
  43. Pritchard, B.P.; Altarawy, D.; Didier, B.; Gibsom, T.D.; Windus, T.L. A New Basis Set Exchange: An Open, Up-to-date Resource for the Molecular Sciences Community. J. Chem. Inf. Model. 2019, 59, 4814–4820. [Google Scholar] [CrossRef]
  44. Feller, D. The role of databases in support of computational chemistry calculations. J. Comput. Chem. 1996, 17, 1571–1586. [Google Scholar] [CrossRef]
  45. Schuchardt, K.L.; Didier, B.T.; Elsethagen, T.; Sun, L.; Gurumoorthi, V.; Chase, J.; Li, J.; Windus, T.L. Basis Set Exchange: A Community Database for Computational Sciences. J. Chem. Inf. Model. 2007, 47, 1045–1052. [Google Scholar] [CrossRef]
  46. Zhurko, G.A.; Zhurko, D.A. ChemCraft. Version 1.6, Build 312. Available online: https://www.chemcraftprog.com/index.html (accessed on 20 March 2023).
  47. Girichev, G.V.; Utkin, A.N.; Revichev, F. Modernization of electron diffraction recorder EMR-100 for gas research. Prib. Tekh. Eksp. 1984, 27, 187. (In Russian) [Google Scholar]
  48. Girichev, G.V.; Shlykov, S.A.; Revichev, Y.F. Equipment for studying the structure of molecules of valence-unsaturated compounds. Prib. Tekh. Eksp. 1986, 4, 167. (In Russian) [Google Scholar]
  49. Girichev, E.G.; Zakharov, A.V.; Girichev, G.V.; Bazanov, M.I. Automation of a physicochemical experiment: Photometry and voltammetry. Izv. Vyssh. Uchebn. Zaved. Tekstiln. Prom. 2000, 2, 142. (In Russian) [Google Scholar]
  50. Andersen, B.; Seip, H.M.; Strand, T.G.; Stolevik, R. Procedure and Computer Programs for the Structure Determination of Gaseous Molecules from Electron Diffraction Data. Acta Chem. Scand. 1969, 23, 3224–3234. [Google Scholar] [CrossRef]
  51. Vishnevskiy, Y.V.; Zhabanov, Y.A. New implementation of the first-order perturbation theory for calculation of interatomic vibrational amplitudes and corrections in gas electron diffraction. J. Phys. Conf. Ser. 2015, 633, 012076. [Google Scholar] [CrossRef]
Molecules 28 03665 g001 550
Figure 1. Optimized structures of Re2F8 molecule: (a) model D4h with an eclipsed conformation; (b) model D4d with a staggered conformation; (c) model D2h with non-equivalent Re-F bonds; (d) model D2h with four Re-Fbr bridging bonds 4; (e) model with an ordinary Re-Re bond of C2h symmetry.
Figure 1. Optimized structures of Re2F8 molecule: (a) model D4h with an eclipsed conformation; (b) model D4d with a staggered conformation; (c) model D2h with non-equivalent Re-F bonds; (d) model D2h with four Re-Fbr bridging bonds 4; (e) model with an ordinary Re-Re bond of C2h symmetry.
Molecules 28 03665 g001
Molecules 28 03665 g002 550
Figure 2. The experimental (circles) reduced molecular scattering intensity sM(s) of the ReF4 vapor at T = 471 K and theoretical (full lines) one, corresponding to the D4h model of Re2F8 molecules, and difference curves ΔsM(s).
Figure 2. The experimental (circles) reduced molecular scattering intensity sM(s) of the ReF4 vapor at T = 471 K and theoretical (full lines) one, corresponding to the D4h model of Re2F8 molecules, and difference curves ΔsM(s).
Molecules 28 03665 g002
Molecules 28 03665 g003 550
Figure 3. Radial distribution functions f(r) (experimental–circles, theoretical—full line) and difference curve Δf(r).
Figure 3. Radial distribution functions f(r) (experimental–circles, theoretical—full line) and difference curve Δf(r).
Molecules 28 03665 g003
Molecules 28 03665 g004 550
Figure 4. Diagram and view of the MOs, the main contribution to which is made by dz2, dxz, dyz, and dxy-AO of two Re atoms.
Figure 4. Diagram and view of the MOs, the main contribution to which is made by dz2, dxz, dyz, and dxy-AO of two Re atoms.
Molecules 28 03665 g004
Molecules 28 03665 g005 550
Figure 5. (a) Donor σ(Re1-F) NBO, (b) Acceptor σ*(Re2-F) NBO, (c) result of their interaction. NBOs are built from sp2.7d2.9 hybrid Re orbitals and sp2.5 hybrid F orbitals.
Figure 5. (a) Donor σ(Re1-F) NBO, (b) Acceptor σ*(Re2-F) NBO, (c) result of their interaction. NBOs are built from sp2.7d2.9 hybrid Re orbitals and sp2.5 hybrid F orbitals.
Molecules 28 03665 g005
Molecules 28 03665 g006 550
Figure 6. Potential function of the internal rotation (PFIR) of ReF4 fragments about the Re-Re bond of the Re2F8 molecule.
Figure 6. Potential function of the internal rotation (PFIR) of ReF4 fragments about the Re-Re bond of the Re2F8 molecule.
Molecules 28 03665 g006
Molecules 28 03665 g007 550
Figure 7. Diagram of rhenium 5d AOs and geometric structure of ReF4.
Figure 7. Diagram of rhenium 5d AOs and geometric structure of ReF4.
Molecules 28 03665 g007
Molecules 28 03665 g008 550
Figure 8. Correlation between Re-X bond energy and internuclear distance r(Re-X).
Figure 8. Correlation between Re-X bond energy and internuclear distance r(Re-X).
Molecules 28 03665 g008
Table
Table 1. Structural parameters of rh1 and rα structures (in Å) of the Re2F8 molecule according to the data of GED experiments and PBE/RECP-3 calculation.
Table 1. Structural parameters of rh1 and rα structures (in Å) of the Re2F8 molecule according to the data of GED experiments and PBE/RECP-3 calculation.
ParametersPBErh1lcalclexprα
[16]		lcalc
[16]		lexp
[16]
Re1-Re22.2592.264 (5)0.0380.046 (2)2.269 (5)0.0350.035 (2)
Re1-F61.8611.846 (4)0.0440.045 (4)1.830 (4)0.0420.041 (5)
F5…F82.5922.573 (6)0.1150.123 (2) 0.1170.122 (16)
F5…F92.9012.887 (9)0.2400.238 (4) 0.1990.192 (8)
Re1…F93.1653.153 (7)0.1160.114 (4)3.123 (10)0.1080.100 (8)
F5…F73.6653.639 (8)0.0710.074 (14) 0.0640.085 (30)
F5…F103.8903.830 (48)0.3140.317 (14) 0.283 ÷ 0.4520.33 (8)
F5…F44.6744.643 (10)0.1150.161 (34) 0.1110.18 (8)
F5Re1Re299.999.7 (2) 98.7 (7)
F4ReReF7 2.4 (3.6)
Rf, % 4.7 7.0
Table
Table 2. AIM/NBO characteristics of Re-F and Re-Re bonds in Re2F8 by PBE0/qRECP-1 data a.
Table 2. AIM/NBO characteristics of Re-F and Re-Re bonds in Re2F8 by PBE0/qRECP-1 data a.
qAIM/qNPA (Re)2.36/1.57
qAIM/qNPA (F)−0.59/−0.39
bondRe-FRe-Re
ε0.0740.000
δAIM/PNBO0.83/0.812.28/2.24
a q—a net charge of an atom, e; ε—a bond ellipticity; δ—a electron delocalization index, e, PNBO—Wiberg bond index.
Table
Table 3. Selected parameters of the Re2F8 molecule and the [Re2F8]2− dianion.
Table 3. Selected parameters of the Re2F8 molecule and the [Re2F8]2− dianion.
r (Re-Re),
Å		r (Re-F),
Å		FReRe, °ν (Re-Re) cm−1νtors
cm−1		q (Re)q (F)
Re2F8 GED, D4h2.264 (5)1.846 (4)99.7 (2)345 a301.57 a−0.39 a
[Re2F8]2− X-ray, D4h2.188 (3) [15]
2.20 [12]		1.95 [12]104.5 a353 a69 a1.23 a−0.56 a
a calculated parameters at PBE/RECP-3 theory level.
Table
Table 4. Selected molecular characteristics of Re2F8, Re2Cl8 and Re2Br8 a.
Table 4. Selected molecular characteristics of Re2F8, Re2Cl8 and Re2Br8 a.
Molecular
Characteristics		Re2F8
D4h		Re2Cl8
D4h		Re2Br8
D4h/D4d
r (Re-Re), Å2.2592.3172.336/2.300
r (Re-X), Å1.8602.2802.441/2.445
Re-Re-X, °99.9101.6102.6/102.0
X-Re-X, °88.387.787.3/87.5
r (X…X), Å2.9013.2343.402/3.786
ΣrVdV (X), Å b2.943.53.9
ν (Re-Re), cm−1338268261/275
νtor (Re-Re), cm−142.620.212.5i/9.1
E (D4d)-E (D4h), kcal/mol2.01.1−1.0
E (Re-Re), kcal/mol106.1101.199.8
E (Re-X), kcal/mol132.775.459.1
a PBE/RECP-3, b ΣrVdV (X)—sum of van der Waals radii.
Table
Table 5. Results of three variants of DFT calculations and experimental data for the Re2F8 molecule.
Table 5. Results of three variants of DFT calculations and experimental data for the Re2F8 molecule.
re (Re-Re)
Å		re (Re-F)
Å		αe (ReReF)
°		ν (Re-Re)
cm−1		νtors (Re-Re)
cm−1		ν (Re-F) a
cm−1
PBE0/qRECP-12.2261.843100.137040617–749
B3LYP/qRECP-22.2881.87199.734510594–710
PBE/RECP-32.2591.86099.933843597–704
GED2.264 (5)1.846 (4)99.8 (0.2) 30
a the range of eight stretching Re-F vibration frequencies (Figure S2).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Giricheva, N.I.; Tverdova, N.V.; Sliznev, V.V.; Girichev, G.V. Dimer Rhenium Tetrafluoride with a Triple Bond Re-Re: Structure, Bond Strength. Molecules 2023, 28, 3665. https://doi.org/10.3390/molecules28093665

AMA Style

Giricheva NI, Tverdova NV, Sliznev VV, Girichev GV. Dimer Rhenium Tetrafluoride with a Triple Bond Re-Re: Structure, Bond Strength. Molecules. 2023; 28(9):3665. https://doi.org/10.3390/molecules28093665

Chicago/Turabian Style

Giricheva, Nina I., Natalia V. Tverdova, Valery V. Sliznev, and Georgiy V. Girichev. 2023. "Dimer Rhenium Tetrafluoride with a Triple Bond Re-Re: Structure, Bond Strength" Molecules 28, no. 9: 3665. https://doi.org/10.3390/molecules28093665

APA Style

Giricheva, N. I., Tverdova, N. V., Sliznev, V. V., & Girichev, G. V. (2023). Dimer Rhenium Tetrafluoride with a Triple Bond Re-Re: Structure, Bond Strength. Molecules, 28(9), 3665. https://doi.org/10.3390/molecules28093665

Article Metrics

Back to TopTop