Probing Reactivity with External Forces: The Case of Nitroacetamides in Water
Abstract
:1. Introduction
2. Results
2.1. Experimental Ionization Constant ()
2.2. Computed Ionization Constant

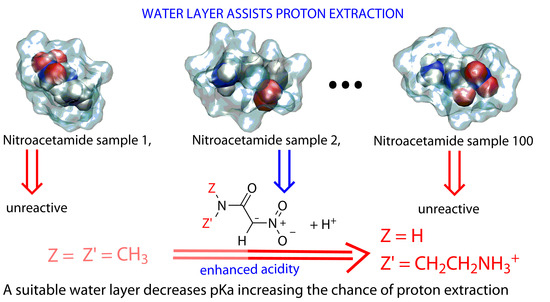
2.3. Trajectories Analysis
3. Discussion
4. Materials and Methods
4.1. Preparation of Nitroacetamides and Their Characterization
4.1.1. N,N-dimethyl-2-nitroacetamide (1)
4.1.2. N-(2-aminoethyl)-2-nitroacetamide hydrochloride (2)
4.1.3. 1-morpholin-4-yl-2-nitro-ethanone (3)
4.2. Determination of Ionization Constants (Apparent )
4.3. Calculation of Ionization Constants
4.3.1. System Preparation
4.3.2. Thermal Equilibration
4.3.3. Density-Functional Tight-Binding MD
4.4. Pulling H in DFTB Models
4.5. Data Analysis
- The simulation of the stochastic regime performed with a deterministic trajectory;
- The high frequency motions sampled in the ps time-scale of BOMD simulation.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cecchi, L.; De Sarlo, F.; Machetti, F. Synthesis of 4,5-Dihydroisoxazoles by Condensation of Primary Nitro Compounds with Alkenes by Using a Copper/Base Catalytic System. Chem. Eur. J. 2008, 14, 7903–7912. [Google Scholar] [CrossRef] [PubMed]
- Baglieri, A.; Meschisi, L.; De Sarlo, F.; Machetti, F. Competitive Copper Catalysis in the Condensation of Primary Nitro Compounds with Terminal Alkynes: Synthesis of Isoxazoles. Eur. J. Org. Chem. 2016, 2016, 4643–4655. [Google Scholar] [CrossRef]
- Bernasconi, C.F.; Pérez-Lorenzo, M.; Brown, S.D. Kinetics of the Deprotonation of Methylnitroacetate by Amines: Unusually High Intrinsic Rate Constants for a Nitroalkane. J. Org. Chem. 2007, 72, 4416–4423. [Google Scholar] [CrossRef] [PubMed]
- Ono, N. The Nitro Group in Organic Synthesis; Organic Nitro Chemistry Series; Wiley-VCH: New York, NY, USA, 2001; pp. 30–125. [Google Scholar] [CrossRef]
- De Sarlo, F.; Machetti, F. Condensation of Primary Nitro Compounds to Isoxazole Derivatives: Stoichiometric to Catalytic. In Methods and Applications of Cycloaddition Reactions in Organic Syntheses; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2014; Chapter 8; pp. 205–222. [Google Scholar] [CrossRef]
- De Sarlo, F.; Machetti, F. Primary nitro compounds: Progress in the synthesis of isoxazoles by condensation with aldehydes or activated ketones. Org. Biomol. Chem. 2023, 21, 7255–7266. [Google Scholar] [CrossRef]
- Pogorelyi, V.K.; Vishnyakova, T.B. The Hydrogen Bond and CH Acidity. Russ. Chem. Rev. 1984, 53, 1154. [Google Scholar] [CrossRef]
- Keeffe, J.R.; Morey, J.; Palmer, C.A.; Lee, J.C. The nitroalkane anomaly—Solvent dependence. J. Am. Chem. Soc. 1979, 101, 1295–1297. [Google Scholar] [CrossRef]
- Ren, J.; Cramer, C.J.; Squires, R.R. Superacidity and Superelectrophilicity of BF3-Carbonyl Complexes. J. Am. Chem. Soc. 1999, 121, 2633–2634. [Google Scholar] [CrossRef]
- Koppel, I.A.; Burk, P.; Koppel, I.; Leito, I. Generalized Principle of Designing Neutral Superstrong Brønsted Acids. J. Am. Chem. Soc. 2002, 124, 5594–5600. [Google Scholar] [CrossRef]
- Bordwell, F.G.; Bartmess, J.E. The Taft equation as applied to equilibrium acidities of nitroalkanes, G(CH2)nNO2. J. Org. Chem. 1978, 43, 3101–3107. [Google Scholar] [CrossRef]
- Perrin, D.D.; Dempsey, B.; Serjeant, E.P. pKa Prediction for Organic Acids and Bases; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar] [CrossRef]
- Hansch, C.; Leo, A. Exploring QSAR: Fundamentals and Applications in Chemistry and Biology; American Chemical Society: Washington, DC, USA, 1995. [Google Scholar]
- Kütt, A.; Tshepelevitsh, S.; Saame, J.; Lõkov, M.; Kaljurand, I.; Selberg, S.; Leito, I. Strengths of Acids in Acetonitrile. Eur. J. Org. Chem. 2021, 2021, 1407–1419. [Google Scholar] [CrossRef]
- Abboud, J.L.M.; Koppel, I.A.; Uggerud, E.; Leito, I.; Koppel, I.; Sekiguchi, O.; Kaupmees, K.; Saame, J.; Kütt, K.; Mishima, M. Solution and Gas-Phase Acidities of all-trans (all-E) Retinoic Acid: An Experimental and Computational Study. Chem. Eur. J. 2015, 21, 11238–11243. [Google Scholar] [CrossRef] [PubMed]
- La Penna, G.; Machetti, F. Understanding the Exceptional Properties of Nitroacetamides in Water: A Computational Model Including the Solvent. Molecules 2018, 23, 3308. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Raamat, E.; Kaupmees, K.; Ovsjannikov, G.; Trummal, A.; Kütt, A.; Saame, J.; Koppel, I.; Kaljurand, I.; Lipping, L.; Rodima, T.; et al. Acidities of strong neutral Brønsted acids in different media. J. Phys. Org. Chem. 2013, 26, 162–170. [Google Scholar] [CrossRef]
- Greenstein, J.P. Studies of the peptides of trivalent amino acids: III. The apparent dissociation constants, free energy changes, and heats of ionization of peptides involving arginine, histidine, lysine, tyrosine, and aspartic and glutamic acids, and the behavior of lysine peptides toward nitrous acid. J. Biol. Chem. 1933, 101, 603–621. [Google Scholar] [CrossRef]
- Isom, D.G.; Castañeda, C.A.; Cannon, B.R.; García-Moreno, B.E. Large shifts in pKa values of lysine residues buried inside a protein. Proc. Natl. Acad. Sci. USA 2011, 108, 5260–5265. [Google Scholar] [CrossRef]
- Sigel, H.; Martin, R.B. Coordinating Properties of the Amide Bond. Stability and Structure of Metal Ion Complexes of Peptides and Related Ligands. Chem. Rev. 1982, 82, 385–426. [Google Scholar] [CrossRef]
- Onufriev, A.V.; Case, D.A. Generalized Born Implicit Solvent Models for Biomolecules. Annu. Rev. Biophys. 2019, 48, 275–296. [Google Scholar] [CrossRef]
- Machetti, F.; Bucelli, I.; Indiani, G.; Kappe, C.O.; Guarna, A. Parallel Synthesis of an Amide Library Based on the 6,8-Dioxa-3-azabicyclo[3.2.1]octane Scaffold by Direct Aminolysis of Methyl Esters. J. Comb. Chem. 2007, 9, 454–461. [Google Scholar] [CrossRef]
- Ciommer, B.; Frenking, G.; Schwarz, H. Massenspektrometrische Untersuchung von Stickstoffverbindungen, XXXI, Experimentelle und theoretische Untersuchungen zur dissoziativen Ionisierung von α-nitro- und α-halogen substituierten Acetamiden. Pseudo-einstufige Zerfallsprozesse von Radikalkationen in der Gasphase. Chem. Ber. 1981, 114, 1503–1519. [Google Scholar] [CrossRef]
- Guideri, L.; De Sarlo, F.; Machetti, F. Conjugate Addition versus Cycloaddition/Condensation of Nitro Compounds in Water: Selectivity, Acid–Base Catalysis, and Induction Period. Chem. Eur. J. 2013, 19, 665–677. [Google Scholar] [CrossRef] [PubMed]
- Lyapkalo, I.M.; Ioffe, S.L.; Strelenko, Y.A.; Tartakovsky, V.A. A novel general method for the synthesis of nitrones by reaction of nitroso compounds with anions of aliphatic nitro compounds. Russ. Chem. Bull. 1996, 45, 856–862. [Google Scholar] [CrossRef]
- Harvey, D. Functions for Generating and Plotting Titration Curves; The Comprehensive R Archive Network, 2016–2022. Available online: https://cran.r-project.org/package=titrationCurves (accessed on 14 December 2023).
- De Levie, R. Principles of Quantitative Chemical Analysis; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Elstner, M.; Porezag, D.; Jungnickel, G.; Elsner, J.; Haugk, M.; Frauenheim, T.; Suhai, S.; Seifert, G. Self-consistent-charge Density-functional Tight-binding Method for Simulations of Complex Materials Properties. Phys. Rev. B 1998, 58, 7260–7268. [Google Scholar] [CrossRef]
- Aradi, B.; Hourahine, B.; Frauenheim, T. DFTB+, a Sparse Matrix-Based Implementation of the DFTB Method. J. Phys. Chem. A 2007, 111, 5678–5684. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.J. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD visual molecular dynamics. J. Molec. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in ’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comp. Phys. Comm. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and Testing of the OPLS All-Atom Force Field On Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Kaminski, G.A.; Friesner, R.A.; Tirado-Rives, J.; Jorgensen, W.L. Evaluation and Reparametrization of the OPLS-AA Force Field for Proteins via Comparison with Accurate Quantum Chemical Calculations on Peptides. J. Phys. Chem. B 2001, 105, 6474–6487. [Google Scholar] [CrossRef]
- Selvåg, J.; Kuznetsova, T.; Kvamme, B. Molecular dynamics study of surfactant-modified water-carbon dioxide systems. Mol. Sim. 2018, 44, 128–136. [Google Scholar] [CrossRef]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation; Academic Press: San Diego, CA, USA, 1996. [Google Scholar]
- Ryckaert, J.P.; Ciccotti, G.; Berendsen, H.J.C. Numerical Integration of the Cartesian Equations of Motion with Constraints: Molecular Dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef]
- Nosé, S. A Molecular Dynamics Method for Simulations in the Canonical Ensemble. Molec. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic Transitions in Single Crystals: A New Molecular Dynamics Method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Hourahine, B.; Aradi, B.; Blum, V.; Bonafé, F.; Buccheri, A.; Camacho, C.; Cevallos, C.; Deshaye, M.Y.; Dumitricǎ, T.; Dominguez, A.; et al. DFTB+, a software package for efficient approximate density functional theory based atomistic simulations. J. Chem. Phys. 2020, 152, 124101. [Google Scholar] [CrossRef]
- Fletcher, R. Practical Methods of Optimization, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Tribello, G.A.; Bonomi, M.; Branduardi, D.; Camilloni, C.; Bussi, G. PLUMED 2: New feathers for an old bird. Comp. Phys. Commun. 2014, 185, 604–613. [Google Scholar] [CrossRef]
- Barducci, A.; Chelli, R.; Procacci, P.; Schettino, V.; Gervasio, F.L.; Parrinello, M. Metadynamics simulation of prion protein: β-structure stability and the early stages of misfolding. J. Am. Chem. Soc. 2006, 128, 2705–2710. [Google Scholar] [CrossRef]
- van der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J.C. GROMACS: Fast, flexible, and free. J. Comput. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef]
- Bonomi, M.; Branduardi, D.; Bussi, G.; Camilloni, C.; Provasi, D.; Raiteri, P.; Donadio, D.; Marinelli, F.; Pietrucci, F.; Broglia, R.A.; et al. PLUMED: A Portable Plugin for Free-Energy Calculations with Molecular Dynamics. J. Comput. Phys. 2009, 180, 1961–1972. [Google Scholar] [CrossRef]






| mL NaOH | log([HA]/[A]) | pH | |
|---|---|---|---|
| 0.3 | 1.08 | 3.69 | 4.77 |
| 0.6 | 0.745 | 3.95 | 4.69 |
| 0.9 | 0.5278 | 4.21 | 4.74 |
| 1.2 | 0.358 | 4.40 | 4.76 |
| 1.5 | 0.210 | 4.54 | 4.75 |
| 1.8 | 0.0741 | 4.70 | 4.77 |
| 2.1 | −0.0586 | 4.86 | 4.80 |
| 2.4 | −0.194 | 5.01 | 4.82 |
| 2.7 | −0.340 | 5.15 | 4.81 |
| 3.0 | −0.506 | 5.35 | 4.84 |
| 3.3 | −0.716 | 5.61 | 4.89 |
| 3.6 | −1.0313 | 6.02 | 4.99 |
| 3.9 | −2.0470 | 6.78 | 4.73 |
| mL NaOH | log([HA]/[A]) | pH | |
|---|---|---|---|
| 0.3 | 1.0013 | 5.89 | 6.89 |
| 0.6 | 0.655 | 6.26 | 6.91 |
| 0.9 | 0.428 | 6.50 | 6.93 |
| 1.2 | 0.245 | 6.66 | 6.90 |
| 1.5 | 0.0813 | 6.83 | 6.91 |
| 1.8 | 0.0766 | 6.98 | 6.90 |
| 2.1 | 0.240 | 7.15 | 6.91 |
| 2.4 | 0.422 | 7.34 | 6.92 |
| 2.7 | 0.647 | 7.56 | 6.91 |
| 3.0 | 0.987 | 7.89 | 6.90 |
| Model | Total | Non Reactive | Reactive | Faults | Reactive Ratio () |
|---|---|---|---|---|---|
| 1 | 100 | 66 | 5 | 29 | 0.07 |
| 2 | 100 | 80 | 18 | 2 | 0.18 |
| 3 | 100 | 85 | 10 | 5 | 0.11 |
| Compound | aci | enol | nitronate |
|---|---|---|---|
| 1 | 60.9 | 0 | −1107 |
| 2 | −9.3 | 57.3 | −621 |
| 3 | 29.1 | −36.1 | −395.2 |
| Compound | (Equation (8)) | (Exp.) | |
|---|---|---|---|
| 1 | −7.09 | 0 | 0 |
| 2 | −11.59 | −1.95 | −2.47 |
| 3 | −10.04 | −1.28 | −0.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
La Penna, G.; Machetti, F. Probing Reactivity with External Forces: The Case of Nitroacetamides in Water. Molecules 2024, 29, 9. https://doi.org/10.3390/molecules29010009
La Penna G, Machetti F. Probing Reactivity with External Forces: The Case of Nitroacetamides in Water. Molecules. 2024; 29(1):9. https://doi.org/10.3390/molecules29010009
Chicago/Turabian StyleLa Penna, Giovanni, and Fabrizio Machetti. 2024. "Probing Reactivity with External Forces: The Case of Nitroacetamides in Water" Molecules 29, no. 1: 9. https://doi.org/10.3390/molecules29010009
APA StyleLa Penna, G., & Machetti, F. (2024). Probing Reactivity with External Forces: The Case of Nitroacetamides in Water. Molecules, 29(1), 9. https://doi.org/10.3390/molecules29010009