4.1. Mixer Design
In this section, the design concept of the staggered Dean Vortex micromixer is introduced. A parallel lamination micromixer with two-dimensional curved rectangular channels is designed in our study. The centrifugal forces in curved rectangular channels cause fluids to produce secondary flows. A pair of counter-rotating vortices above and below the symmetry plane of the channel coincides with its plane of curvature. The split-and-recombination (SAR) structures of flow channels result in the reduction of the diffusion distance of two fluids. The impinging effects increase the mixing strength when one stream is injected into the other. The fluid properties in our simulations are diffusivity, D, of 4 × 10−10 m2/s, kinematic viscosity, ν, of 1 × 10−6 m2/s, density, ρ, of 1 × 103 kg/m3 and used unless noted otherwise. The flow system is composed of several staggered three-quarter ring-shaped channels. The inner radius, Ri, is 500 μm and outer radius, Ro, is 600 μm. The inlet and outlet have square 100 μm cross-sections.
A particle trajectory is the path of a particle moving in a fluid. Being able to visualize this trajectory can be very helpful in understanding flow patterns and flow distribution. At a steady state, the streak lines coincide with the particle trajectories. These can be thought of as recordings of the paths where fluid elements flow over a certain period and are used to describe the nature of the flow field inside the micromixer. In this study, the particle trajectories are determined by integrating the vector equations of motion and obtain an explicit Lagrangian-type particle tracking scheme from CFD-ACE+
TM software. The integration is done by utilizing a fourth order Runge-Kutta scheme with adaptive step size, and the linear shape function [
18] is used for the spatial interpolation of velocity.
The particle trajectories inside the staggered curved channels at the first segment are shown in
Figure 4. The inlet velocities of two liquids are set at 0.5 m/s, which correspond to a
Re of 50. A front view of the particle trajectories through the mixing channels is depicted in
Figure 4a. The red- and pink-colored trajectories represent species A, and the blue- and dark blue-colored trajectories represent species B. The red- and pink-colored trajectories stretch from the inlet, split into two streams, and merge back into one main stream. It is observed that species A and species B divide after the split part of channel, merge into one stream and re-allocate into two separate channels again. For species A, most of the red-colored trajectories move into the angled channel and only the red-colored trajectories near the outer region keep moving in the original curved channel after the first split part. However, after the second split part, some moves in the original curved channel and some shifts in the angled channel. This flow pattern also can be seen for the pink, blue and dark blue trajectories, respectively. Due to the SAR structures, the fluids switch between the original curved channels and the angled channels and wind along the downstream channels. When the SAR structures of the flow channels result in the reduction of the diffusion distance of two fluids, the mixing performance can be improved.
Figures 4b and c show the particle trajectories around the interconnection of two sub-channels (the region marked by an oval in
Figure 4a) in the vertical views. In
Figure 4b, both species split into two streams and then the contact interface between the two species can be increased. In
Figure 4c, two streams merge and produce an impact around the recombined part. The main stream is deflected when the branch stream impinges on it. This impingement enlarges the mixing strength when one stream is injected into the other.
In an effort to understand two-fluid mixing inside the staggered Dean Vortex micromixer, the velocity vector planes and the cross-sectional concentration distributions are utilized to demonstrate the rotation of fluid flows. Several cross-sectional locations in the structure are expressed in
Figure 5 at a
Re of 50. The images are taken at the first half segment. The fluids flow into the inlet and progress counterclockwise along the curved channel. Dean flows are created in the channel of constant cross-section; one rotates counterclockwise above and the other clockwise below the symmetry plane of the channel (viewed from the direction of the arrow). One stream follows the original channel, and the vortices continue in the same direction. The other stream flows into the branch channel, and the vortices move clockwise above and counterclockwise below the symmetry plane of channel. In vector planes, the length of an arrow means the magnitude of the velocity vector. Compared with the vector planes between the two branch channels, a large amount of fluid tends to flow along the original curved channel (the right-hand side) and the rest of fluid moves into the angled channel (the left-hand side). The uneven split of the two fluids inside the staggered channels can be observed. Then the two channels are recombined, and the two streams merge into a single large one. After leaving this region, the vortices move clockwise above and counterclockwise below the symmetry plane of the channel. Similar flow characteristics can be seen along the downstream. However, the rotating directions of the created Dean vortices are switched. A significant amount of SAR vortex flows exist due to fluids flowing through the staggered curved channels. The ability to sequentially combine these flow regimes creates increased contact surface between the two fluids.
The cross-sectional concentration distributions are also used to demonstrate the mixing characteristics along the downstream channel in
Figure 5. Fluid flows around a curved channel and the fluid near the centre experiences a larger centrifugal force than that near the top and the bottom. The fluid velocity along the central axis is the highest and is the most strongly affected by centrifugal forces. As a result, the liquid flowing along the central axis is thrust outward vigorously by inertial force, and the liquids near the top and the bottom flow inward. Thus, the vertical interface that crosses the central axis is distorted and bell shaped at this location. In the angled channel, blue-colored fluids are surrounded by red-colored fluids. It shows the lamellae of the two species and is accompanied by a corresponding increase in interfacial area. So the combination of SAR, Dean Vortex and a strong impact inside the channel significantly improves mixing.
To evaluate the mixing performances of staggered curved microchannels, the results are compared with the previous work [
12]. In every mixing segment of their design, the microstructure consisted of one three-quarter ring-shaped channel and two three-eighth ring-shaped channels (
i.e., Continuous Curved Channels (CCC) with three-quarter ring-shaped channels). Each segment of our design is comprised of 3 staggered curved channels which are three-eighth ring-shaped and three-quarter ring-shaped (
i.e., Staggered Curved Channels (SCC)). Our micromixer has the same separate microstructures as the previous design; however, the path length per segment is different, as shown in
Figure 6a. In order to evaluate the mixing performances between the staggered curved microchannels and the continuous curved microchannels, a microstructure which is composed of one semi-circular channel and two three-quarter ring-shaped channels is also introduced (
i.e., Continuous Curved Channels (CCC) with semi-circular channels). The path length per segment of the former structure is the same as that of our designed micromixer. This work also examines a microchannel with a straight section. The geometric design of the proposed CCC is modified and scaled to be a similar size to that of our mixer.
Figure 6b shows the mixing indices of a comparative analysis that was performed across four designs at an inlet flow velocity of 0.1 m/s and
Re of 10, which corresponds to a Dean number (
K) of 4.47 and a Péclet number (
Pe) of 25000. The SAR channel and the fluid impact effect in the SCC improve fluidic mixing. The mixing performance shows improvement in
Figure 6b. For the larger path length per segment of CCC with three-quarter ring-shaped channels, the mixing due to the secondary flows induced by the centrifugal force is larger than that of CCC with semi-circular channels. The effect of centrifugal forces on the mixing of CCC with semi-circular channels can be seen, and the mixing is better than that of the channel with a straight section. Lack of staggered geometries results in poorer mixing compared with the mixing index between SCC and CCC with the same path length per segment. It is found that little mixing occurs in the channel with a straight section. This difference is attributed to the creation of two vortices in the curved channels, which promote mixing. The general trend of present computational results agrees well with those of the previous results. Based on the same path length per segment it is clear that the mixing index of present geometry is considerably improved compared to the other designs.
In addition to mixing index, the pressure drop is also an important issue in the design of micromixers. The pressure drops in the microchannels with four segments are 5913.27 Pa, 2754.33 Pa, 3958.09 Pa and 3956.35 Pa for the CCC with three-quarter ring-shaped channels, the SCC, the CCC with semi-circular channels and the channel with a straight section, respectively. The SCC has the lowest pressure drop among these channels. Each segment of our micromixer is comprised of 3 curved channels with uniform width. The flow rate in each sub-channel is reduced compared to the main channel. Despite the existence of the additional bends and the presence of the Dean vortices, the pressure drop of the SCC is less compared to the channel with a straight section. Besides, the SCC has a higher mixing index than the straight microchannel from
Figure 5b.
The front views of the images along the downstream direction were commonly used to qualitatively characterize the mixing performance of a micromixer. In our work, the front view of the color changes along the downstream direction are captured by a microscope and CCD camera with a graphic grabber system. When phenolphthalein meets and reacts with NaOH, it changes its color from colorless to purple so that the interface between two streams can be identified by a purple color. In the case of the continuous curved channels with three-quarter ring-shaped channels at
Re equal to 10, as shown in
Figure 7a, two streams flowing in parallel meet each other exactly at the central line of the channel and thus the interface is clearly observed near the inlet part of the channel. The thickness of the purple region increases along the downstream obviously due to the secondary flows. The color intensity indicates the level of mixing in the curved channel. With regard to
Figure 7b, staggered curved channels, much more reacted solution stream passes through the inner half of the channel and the variation of the concentration distribution along the radical direction can be seen clearly. By the naked eye, we can obviously tell the superiority of the SCC over the CCC with three-quarter ring-shaped channels.
4.2. Parametric Study
The effects of various Reynolds numbers on the flow fields and the mixing characteristics inside the microfluidic system are examined. The comparisons of the mixing obtained from numerical analysis and experimental visualization are demonstrated.
Figure 8 shows the numerical and the reacted phenolphthalein imaging results of staggered Dean Vortex micromixers in four representative regions along the downstream direction at various
Re. The flow is from left to right. In
Figure 8, the simulations shown on top are taken at the middle planes of channel height and the concentration distributions are demonstrated. The experimental images are shown on the bottom. The purple-colored streams represent the reacted phenolphthalein at the interface between the phenolphthalein and NaOH streams. In our work, two syringes are loaded with 0.31 mol/L phenolphthalein and 0.33 mol/L NaOH dissolved in 99% ethanol. The effect of the amount of phenolphthalein and NaOH on fluid properties is neglected. The fluid properties are set at the physical and thermodynamic properties of ethanol [
19]. The fluid properties of ethanol used in
Figure 8 are diffusivity,
D, of 1 × 10
−9 m
2/s, kinematic viscosity,
ν, of 1.52 × 10
−6 m
2/s, density,
ρ, of 0.79 × 10
3 kg/m
3.
At
Re = 1 in
Figure 8a, the flows follow the contours of the curved channel. As the flow proceeds forward, a little more solution moves toward the inner part of the channel. The mixing of two fluids is only through molecular diffusion across the interface of the two liquids. However, Dean vortex flows can be created at
Re greater than 10, as shown in
Figure 8b. The interface surface deforms along the downstream. It shows that a more reacted solution stream passes through the inner half of the channel and the variation of the concentration distribution along the radial direction can be seen clearly. At a
Re = 50 in
Figure 8c, two fluids are folded into each other and split into multiple streams due to the large vortex flow combined with the SAR effect and the impact effect. Notably, because of the increases of the interfaces of the two fluids, reacted phenolphthalein streams are increased and mixing is improved. The results of the numerical simulations show that an enlarged interfacial surface area is increased considerably, especially for the case where
Re is equal to 50. Due to numerical diffusion, simulations show better mixing than experiments. However, the comparison between the experimental data and numerical results shows a very reasonable agreement.
Figure 9 shows cross-sectional mixing behaviors in the staggered Dean Vortex micromixers at five locations observed by means of a confocal microscope. The mixing results are taken at five representative positions, such as the inlet, the first, the second, the third and the fourth segments beyond the inlet in the downstream direction, marked by red lines. Around the inlet region of the SCC, only the half-zone containing Rhodamine shows a bright image as a result of laser scanning. The interface between streams is distorted as it moves downstream. The fluid near the centre experiences a larger centrifugal force than that near the top and the bottom. Consequently the liquid flowing along the central axis is forced outward (from left to right), and the liquids near the top and the bottom flow inward (from right to left). Thus the stretching of the interface can be presented and enhance mixing. We found that fluids are mixed well and the interface is distorted at a high
Re. As demonstrated by the confocal microscope images in
Figure 9, the staggered Dean Vortex micromixer can be regarded as a well-designed passive micromixer to achieve almost complete mixing in a manageable length of channel. The results are also compared with the numerical results and a similar trend can be shown.
The mixing performance of two fluids, phenolphthale and NaOH dissolved in ethanol, at specific segments is demonstrated in
Figure 10. The influences of various
Re on the mixing index is depicted. Each normalized intensity is marked by the different symbols is plotted at the abscissa corresponding to different
Re. At low
Re, 0.5 <
Re < 1, viscous forces in the fluid are larger than inertial forces; thus, inertia can be neglected. Mixing within the stated range of
Re is dominated by pure molecular diffusion. The time of contact between the two fluids is sufficiently long enough to generate significant mixing when
Re is small. The mixing index then decreases as the
Re increases within the range of 0.5–1. As the
Re rises to 5, the inertial force increases but the centrifugal force acting on the fluids is still weak. The secondary flow is not strong enough to induce sufficient rotation. The mixing index increases with increasing
Re when
Re is greater than 10; the increased inertial force enlarges the contact area between the two fluids. From the preliminary studies on the micromixer with curved channels, Dean vortex flows can be created at
Re greater than 10. Thus the deformation of interfacial lines is profoundly affected by secondary flow and related to the mixing characteristics. When the
Re is equal to 50, the fluids experience several segments of rotation, SAR and impact consequence. Accompanied by a corresponding increase in interfacial area, good mixing at the channel end has been achieved.
The dashed line in
Figure 10 represents a mixing index equal to 0.9 which denotes that mixing fluids are in a well mixed status. The mixing length is the channel length required for achieving the mixing index of 0.9. And it is a distance that a fluid will keep its original characteristics before dispersing into the surrounding fluid. By means of the mixing length, the required channel length of the micromixer can be demonstrated. The resulting mixing lengths are at the tenth segment, over the twenty-second segment, twentieth segment, seventeenth segment, sixteenth segment, and sixth segment at
Re of 0.5, 1, 5, 10, 25 and 50, respectively. The mixing index at
Re of 50 reaching to 0.9 at the sixth segment is not shown in
Figure 10. These correspond to the downstream distances of 35 mm, 77 mm, 70 mm, 60 mm, 56 mm, and 21 mm. At the
Re of 50, the achieved mixing length (
i.e., 21 mm) is 4 times shorter compared to the case where the
Re equals 1 (
i.e., 77 mm).
4.3. Micromixer Optimization
The performance parameter defined for this study is the mixing quality. The selection of the appropriate design variables that affect mixing quality is one of the most important aspects of design optimization. Among the geometric variables shown in
Figure 1a, the angle between the lines from the center to the two intersections of two consecutive curved channels,
θ, and the angle between two lines of the centers of three consecutive curved channels,
ϕ, are selected as the design variables for optimization. The effect of various inner radius and outer radius on mixing is included and related with the design variable,
θ. It means that the effect of various channel widths (the difference between the inner radius and the outer radius of channels) on mixing is also associated with the design variable,
θ. The design space is selected through the method of steepest ascent [
20].
The first step in obtaining the optimum response settings is to explore the region around the current operating conditions to decide what direction needs to be taken to move towards the optimum region. A first order regression model is utilized at the current operating conditions because the operating conditions are normally far from the optimum response settings. The range of the factors for this design are chosen to be (80°, 90°) for θ and (10°, 30°) for ϕ. The unreplicated 22 design is augmented with one run at the center point (85°, 20°) to check for model adequacy. Then the first order regression model at an inlet flow velocity of 0.25 m/s, which corresponds to the Reynolds number of 25, is expressed as:
where the p values of two design variables are less than 0.05. pθ and pϕ are 0.004 and 0.001, respectively. And the p value of the interaction of two design variable, equal to 0.8215, is larger than 0.05. So the factors affect the response significantly but their interaction does not affect the response.
Extensive numerical simulations were conducted by changing the physical characteristics of
θ and
ϕ.
Figure 11a,b show the relationship between the design variable and the performance parameter and depict the mixing index as a function of
θ and
ϕ, respectively.
Re of 25 are considered. Results show that the mixing index exhibits a monotonic increase with the increasing of
θ and
ϕ. Compared to the first order regression model, we can also find that a similar trend is shown and the mixing index increases as
θ or
ϕ increases.
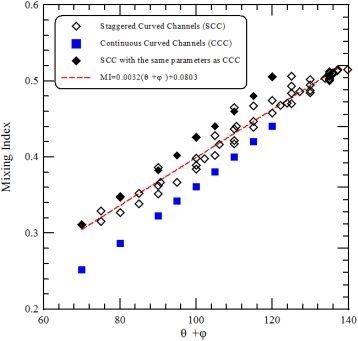
Figure 11c shows a linear relationship between the mixing index and the sum of
θ and
ϕ of staggered curved channels. The linear relationship is given by
where
a is around 0.003166, and
b is around 0.08226. It can be found that the maximal mixing index is related with the maximal value of the sum of
θ and
ϕ. The effect of
ϕ on the mixing index of continuous curved channels with the same path length per segment as the SCC is also shown in
Figure 11c. The intersection of two consecutive curves of continuous curved channels is located at a point, and
θ does not exist. We take
θ equal to 70° as a base reference. Results show that the mixing index of continuous curved channels (marked by blue square points in
Figure 11c) increases with the increasing of
ϕ and is less than that of staggered curved channels with the same values of the sum of
θ and
ϕ (marked by black diamond points in
Figure 11c).
The maximal mixing index is associated with the maximal value of the sum of
θ and
ϕ from
Figure 11c. And these design variables,
θ and
ϕ, are determined by the inner and outer radii of the curved channel and the distances between the centers of three consecutive curved channels. In order to perform the optimization of staggered Dean Vortex micromixers, the relationship between the ratio of the inner radius to the outer radius and the design variables should be found. Due to the geometric constraints of staggered curved channels, the ranges of
θ and
ϕ are limited. In
Figure 12a, the minimum value of
θ can be determined by
where the minimum value of
θ is dependent on the ratio of the inner radius to the outer radius of the curved channel. It also means that the design variable,
θ, is chosen and the effects of various inner radii and outer radii on mixing are included. For example, when
Ri is 500 μm and
Ro is 600 μm, then the minimum of
θ is about 67.1°. In
Figure 12b, the maximum value of
θ can be determined by
where the maximum value of θ is 120° and is a constant.
The maximum length between the centers of consecutive circles,
Lo, is shown in
Figure 12c. The relationship between
Lo and
Ro is expressed as
where the maximum value of
θ or
ϕ can be determined by the above inequality. From
Figure 11c, the maximal mixing index is related with the maximal value of the sum of
θ and
ϕ. The maximal value of the sum of
θ and
ϕ can be found by following. An auxiliary function
f (
θ, ϕ) =
θ +
ϕ is set and
is introduced into the auxiliary function. Then the maximal value of the sum of
θ and
ϕ can be solved numerically and is around 139.82° where
θ is around 106.21°,
i.e.,
Ri/
Ro = 0.601, and
ϕ is around 33.62°. Therefore, the maximal mixing index can be found for any staggered Dean Vortex micromixers when
This relationship can help researchers who are interested in designing staggered Dean Voxter micromixers.
Figure 13 shows the results of a comparative analysis at a
Re equal to 25 that are performed across the three designs, viz., staggered curved channels with
θ equal to 106.2° and
ϕ equal to 33.6°, staggered curved channels with
θ equal to 90° and
ϕ equal to 0° and continuous curved channels with three-quarter ring-shaped channels. It is clear that the mixing is considerably improved throughout the channel length by optimization. The values of the mixing index achieved at the exit for the optimal and the other geometries represent a relative increase of about 12.5% in mixing.