Instrumentation on Multi-Scaled Scattering of Bio-Macromolecular Solutions
Abstract
:1. Introduction
1.1. Motivation
1.2. Classical Approaches to Reduce Multiple Scattering
1.3. Cross Correlation Function Approach
1.4. In Combination with Synchrotron X-ray Scattering
2. Results and Discussion
2.1. Considerations for Combined PCCF with SAXS/WAXD—Sample Cell Design
- (1)
- An ultra-thin wall quartz capillary (with 2.0 mm outer diameter) was used. The wall thickness was about 10 μm.
- (2)
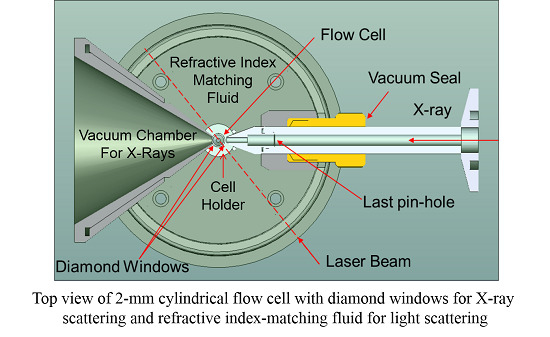
- A tube directly connected to the X-ray collimation system ends very closely to the quartz capillary (about 0.3 mm). This tube, together with the collimation system as a whole, could be evacuated. The third pinhole, as described in the Experimental Section, was mounted inside this tube. A diamond window (in blue color, as shown in Figure 1) with an effective aperture diameter of 2.5 mm and a thickness of 0.25 mm was used at the end of the tube. Background scattering before the sample was, therefore, reduced to a large extent.
- (3)
- After the capillary, a receiver cone with the same diamond window (in blue color, as shown in Figure 1) as used in the collimation tube containing the third pinhole was placed very close (about 0.5 mm) to the opposite side of the capillary. The scattered beam, together with the incident X-ray beam, passed through the diamond window into a vacuum chamber before reaching the wire detector.
- (4)
- Water (HPLC grade) was used as an index-matching fluid, which caused less scattering/absorption when compared with silicon oil in the two narrow gaps between the capillary cell and the two diamond windows.
 ) for X-ray scattering measurements and refractive index-matching fluid for light scattering.
) for X-ray scattering measurements and refractive index-matching fluid for light scattering.
 ) for X-ray scattering measurements and refractive index-matching fluid for light scattering.
) for X-ray scattering measurements and refractive index-matching fluid for light scattering.


2.2. 3D-PCCS Demonstration

2.3. Experimental Test on X-ray Instrumentation in the Combined Facility

3. Experimental Section
3.1. PCCF Techniques
3.1.1. Cross Correlation and Two-Color Approaches
3.1.2. 3D Photon Cross-Correlation Function (3D-PCCF)
Basic Scheme

Current Apparatus Specification

Geometrical Considerations for Combined 3D-PCCF and Synchrotron SAXS/WAXD


Diagrams and Photographs of 3D-PCCF Components


3D-PCCF Alignment
- (1)
- The two laser beams must be precisely crossed at the center of the sample cell. Any mis-alignment of the beams will not only cause the two momentum transfer vectors not to be identical but also to reduce the overlapping region of the two beams, causing various inefficiencies for the cross-correlation function.
- (2)
- The two detectors should look at exactly the same speckle. It is often observed that the two detectors can achieve a good beating efficiency in the auto-correlation mode while generating only a poor cross-correlation signal. Assuming that the beams are well crossed, this is likely caused by the two detectors looking at different speckles with independent temporal correlations.
3.2. Synchrotron SAXS Measurements
3.2.1. Upgrade of Collimation System for SAXS/WAXD



3.2.2. Collimation Control Procedures
3.3. Cell for Liquid Samples

4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chu, B. Laser Light Scattering, 2nd ed.; Academic Press: San Diego, CA, USA, 1991. [Google Scholar]
- Berne, B.J.; Pecora, R. Dynamic Light Scattering: With Applications to Chemistry, Biology, and Physics; Dover Publications: Mineola, NY, USA, 2000. [Google Scholar]
- Chu, B. Dynamic light scattering. In Soft Matter Characterization; Borsali, R., Pecora, R., Eds.; Springer: New York, NY, USA, 2008. [Google Scholar]
- Dhont, J.K.G.; de Kruif, C.G.; Vrij, A. Light scattering in colloidal dispersions: Effects of multiple scattering. J. Colloid Interface Sci. 1985, 105, 539–551. [Google Scholar] [CrossRef]
- Van Veluwen, A.; Lekkerkerker, H.N.W.; de Kruif, C.G.; Vrij, A. Brownian diffusivities of interacting colloidal particles measured by dynamic light scattering. Faraday Discuss. Chem. Soc. 1987, 83, 59–67. [Google Scholar] [CrossRef]
- Vrij, A.; Jansen, J.W.; Dhont, J.K.G.; Pathmamanoharan, C.; Kops-Werkhoven, M.M.; Fijnaut, H.M. Light scattering of colloidal dispersions in non-polar solvents at finite concentrations. Silica spheres as model particles for hard-sphere interactions. Faraday Discuss. Chem. Soc. 1983, 76, 19–35. [Google Scholar] [CrossRef]
- Van Megen, W.; Underwood, S.M.; Pusey, P.N. Dynamics of hard spherical colloids from the fluid to the glass. J. Chem. Soc. Faraday Trans. 1991, 87, 395–401. [Google Scholar] [CrossRef]
- Thomas, J.C.; Tjin, S.C. Fiber optic dynamic light scattering (FODLS) from moderately concentrated suspensions. J. Colloid Interface Sci. 1989, 129, 15–31. [Google Scholar] [CrossRef]
- Wiese, H.; Horn, D. Single-mode fibers in fiber-optic quasielastic light scattering: A study of the dynamics of concentrated latex dispersions. J. Chem. Phys. 1991, 94, 6429–6443. [Google Scholar] [CrossRef]
- Stieber, F.; Richtering, W. Fiber-optic-dynamic-light-scattering and two-color-cross-correlation studies of turbid, concentrated, sterically stabilized polystyrene latex. Langmuir 1995, 11, 4724–4727. [Google Scholar] [CrossRef]
- Weitz, D.A.; Pine, D.J. Diffusing-wave spectroscopy. In Dynamic Light Scattering: The Method and Some Applications; Brown, W., Ed.; Oxford University Press: New York, NY, USA, 1993. [Google Scholar]
- Maret, G. Diffusing-wave Spectroscopy. Curr. Opin. Colloid Interface Sci. 1997, 2, 251–257. [Google Scholar] [CrossRef]
- Urban, C.; Schurtenberger, P. Characterization of turbid colloidal suspensions using light scattering techniques combined with cross-correlation methods. J. Colloid Interface Sci. 1998, 207, 150–158. [Google Scholar] [CrossRef] [PubMed]
- Schätzel, K. Suppression of multiple scattering by photon cross-correlation techniques. J. Mod. Opt. 1991, 38, 1849–1865. [Google Scholar] [CrossRef]
- Pusey, P.N. Suppression of multiple scattering by photon cross-correlation techniques. Curr. Opin. Colloid Interface Sci. 1999, 4, 177–185. [Google Scholar] [CrossRef]
- Overbeck, E.; Sinn, C. Three-dimensional dynamic light scattering. J. Mod. Opt. 1999, 46, 303–326. [Google Scholar] [CrossRef]
- Urban, C.; Schurtenberger, P. Dynamic light scattering in turbid suspensions: An application of different cross-correlation experiments. In Trends in Colloid and Interface Science XII; Koper, G., Bedeaux, D., Cavaco, C., Sager, W., Eds.; Steinkopff: Darmstadt, Germany, 1998; Volume 110, pp. 61–65. [Google Scholar]
- Medebach, M.; Freiberger, N.; Glatter, O. Dynamic light scattering in turbid nonergodic media. Rev. Sci. Instrum. 2008, 79, 15–31. [Google Scholar] [CrossRef]
- Aberle, L.B.; Hülstede, P.; Wiegand, S.; Schröer, W.; Staude, W. Effective suppression of multiply scattered light in static and dynamic light scattering. Appl. Opt. 1998, 37, 6511–6524. [Google Scholar] [CrossRef] [PubMed]
- Overbeck, E.; Sinn, C.; Palberg, T.; Schätzel, K. Probing dynamics of dense suspensions: Three-dimensional cross-correlation technique. Colloids Surf. A 1997, 122, 83–87. [Google Scholar] [CrossRef]
- Moussaïd, A.; Pusey, P.N. Multiple Scattering suppression in static light scattering by cross-correlation spectroscopy. Phys. Rev. E 1999, 60, 5670–5676. [Google Scholar] [CrossRef]
- Guinier, A.; Fournet, G. Small-Angle Scattering of X-rays; Wiley: New York, NY, USA, 1955. [Google Scholar]
- Glatter, O.; Kratky, O. Small Angle X-ray Scattering; Academic Press: New York, NY, USA, 1982. [Google Scholar]
- Guinier, A. X-ray Diffraction in Crystals, Imperfect Crystals, and Amorphous Bodies; Dover Books on Physics Series; Dover: Mineola, NY, USA, 1994. [Google Scholar]
- Glabe, C.G. Structural classification of toxic amyloid oligomers. J. Biol. Chem. 2008, 283, 29639–29643. [Google Scholar] [CrossRef] [PubMed]
- Walsh, D.M.; Selkoe, D.J. Aβ oligomers—A decade of discovery. J. Neurochem. 2007, 101, 1172–1184. [Google Scholar] [CrossRef] [PubMed]
- Moitzi, C.; Vavrin, R.; Bhat, S.K.; Stradner, A.; Schurtenberger, P. A new instrument for time-resolved static and dynamic light-scattering experiments in turbid media. J. Colloid Interface Sci. 2009, 336, 565–574. [Google Scholar] [CrossRef] [PubMed]
- Block, I.D.; Scheffold, F. Modulated 3D cross-correlation light scattering: Improving turbid sample characterization. Rev. Sci. Instrum. 2010, 81, 123107. [Google Scholar] [CrossRef] [PubMed]
- Burger, C.; Hao, J.; Ying, Q.; Isobe, H.; Sawamura, M.; Nakamura, E.; Chu, B. Multilayer vesicles and vesicle clusters formed by the fullerene-based surfactant C60(CH3)5K. J. Colloid Interface Sci. 2004, 275, 632–641. [Google Scholar] [CrossRef] [PubMed]
- Provencher, S.W. A constrained regularization method for inverting data represented by linear algebraic or integral equations. Comput. Phys. Commun. 1982, 27, 213–227. [Google Scholar] [CrossRef]
- Provencher, S.W. CONTIN: A general purpose constrained regularization program for inverting noisy linear algebraic and integral equations. Comput. Phys. Commun. 1982, 27, 229–242. [Google Scholar] [CrossRef]
- Phillies, G.D.J. Suppression of multiple scattering effects in quasielastic light scattering by homodyne cross-correlation techniques. J. Chem. Phys. 1981, 74, 260–262. [Google Scholar] [CrossRef]
- Phillies, G.D.J. Experimental demonstration of multiple-scattering suppression in quasielastic-light-scattering spectroscopy by homodyne coincidence techniques. Phys. Rev. A 1981, 24, 1939–1943. [Google Scholar] [CrossRef]
- Drewel, M.; Ahrens, J.; Podschus, U. Decorrelation of multiple scattering for an arbitrary scattering angle. J. Opt. Soc. Am. A 1990, 7, 206–210. [Google Scholar] [CrossRef]
- Schätzel, K.; Drewel, M.; Ahrens, J. Suppression of multiple scattering in photon correlation spectroscopy. J. Phys. Condens. Matter 1990, 2, SA393–SA398. [Google Scholar] [CrossRef]
- Segrè, P.N.; van Megen, W.; Pusey, P.N.; Schatzel, K.; Peters, W. Two-colour dynamic light scattering. J. Mod. Opt. 1995, 42, 1929–1952. [Google Scholar] [CrossRef]
- LS Instrument, Inc. Available online: http://www.lsinstruments.ch/ (accessed on 23 November 2014).
- Svergun, D.I.; Koch, M.J.H. Small-angle scattering studies of biological macromolecules in solution. Rep. Prog. Phys. 2003, 66, 1735. [Google Scholar] [CrossRef]
- Chu, B.; Harney, P.J.; Li, Y.; Linliu, K.; Yeh, F.; Hsiao, B.S. A laser-aided prealigned pinhole collimator for synchrotron X-rays. Rev. Sci. Instrum. 1994, 65, 597–602. [Google Scholar] [CrossRef]
- Chu, B.; Hsiao, B.S. Small-angle X-ray scattering of polymers. Chem. Rev. 2001, 101, 1727–1762. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, B.; Fang, D.; Mao, Y. Instrumentation on Multi-Scaled Scattering of Bio-Macromolecular Solutions. Int. J. Mol. Sci. 2015, 16, 10016-10037. https://doi.org/10.3390/ijms160510016
Chu B, Fang D, Mao Y. Instrumentation on Multi-Scaled Scattering of Bio-Macromolecular Solutions. International Journal of Molecular Sciences. 2015; 16(5):10016-10037. https://doi.org/10.3390/ijms160510016
Chicago/Turabian StyleChu, Benjamin, Dufei Fang, and Yimin Mao. 2015. "Instrumentation on Multi-Scaled Scattering of Bio-Macromolecular Solutions" International Journal of Molecular Sciences 16, no. 5: 10016-10037. https://doi.org/10.3390/ijms160510016
APA StyleChu, B., Fang, D., & Mao, Y. (2015). Instrumentation on Multi-Scaled Scattering of Bio-Macromolecular Solutions. International Journal of Molecular Sciences, 16(5), 10016-10037. https://doi.org/10.3390/ijms160510016