Optical Absorption Spectra and Electronic Properties of Symmetric and Asymmetric Squaraine Dyes for Use in DSSC Solar Cells: DFT and TD-DFT Studies
Abstract
:1. Introduction
2. Results and Discussion
2.1. Molecular Geometries
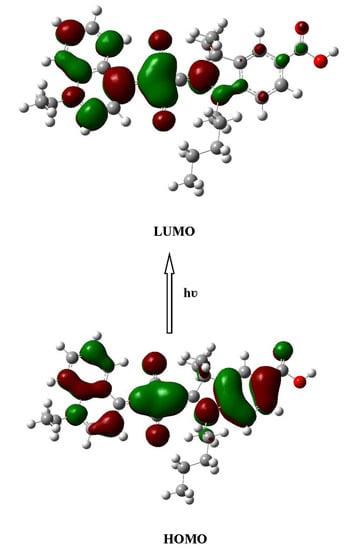
2.2. Electronic Absorption Spectra
2.3. Aromaticcity Computation
3. Materials and Methods
3.1. UV–Visible Absorption Spectra of Squaraine Dyes (SQD1–SQD4)
3.2. Computational Methods
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- O’Regan, B.; Grätzel, M. A low-cost, high-efficiency solar cell based on dye sensitized colloidal TiO2 films. Nature 1991, 353, 737–740. [Google Scholar] [CrossRef]
- Nazeeruddin, M.K.; Kay, A.; Rodicio, I.; Humphry-Baker, R.; Mueller, E.; Liska, P.; Vlachopoulos, N.; Grätzel, M. Conversion of light to electricity by cis-X2bis (2,2’-bipyridyl-4,4’-dicarboxylate)ruthenium(II) charge-transfer sensitizers (X = Cl−, Br−, I−, CN−, and SCN−) on nanocrystalline titanium dioxide electrodes. J. Am. Chem. Soc. 1993, 115, 6382–6390. [Google Scholar] [CrossRef]
- Nazeeruddin, M.K.; Péchy, P.; Renouard, T.; Zakeeruddin, S.M.; Humphry-Baker, R.; Comte, P.; Liska, P.; Cevey, L.; Costa, E.; Shklover, V.; et al. Engineering of efficient panchromatic sensitizers for nanocrystalline TiO2-based solar cells. J. Am. Chem. Soc. 2001, 123, 1613–1624. [Google Scholar] [CrossRef] [PubMed]
- Nazeeruddin, M.K.; Angelis, F.D.; Fantacci, S.; Selloni, A.; Viscardi, G.; Liska, P.; Ito, S.; Takeru, B.; Grätzel, M. Combined experimental and DFT-TDDFT computational study of photoelectrochemical cell ruthenium sensitizers. J. Am. Chem. Soc. 2005, 127, 16835–16847. [Google Scholar] [CrossRef] [PubMed]
- Gao, F.; Wang, Y.; Shi, D.; Zhang, J.; Wang, M.; Jing, X.; HumphryBaker, R.; Wang, P.; Zakeeruddin, S.M.; Grätzel, M. Enhance the optical absorptivity of nanocrystalline TiO2 film with high molar extinction coefficient ruthenium sensitizers for high performance dye-sensitized solar cells. J. Am. Chem. Soc. 2008, 130, 10720–10728. [Google Scholar] [CrossRef] [PubMed]
- Alex, S.; Santhosh, U.; Das, S. Dye sensitization of nanocrystalline TiO2: Enhanced efficiency of unsymmetrical versus symmetrical squaraine dyes. J. Photochem. Photobiol. A 2005, 172, 63–71. [Google Scholar] [CrossRef]
- Chen, Y.; Zeng, Z.; Li, C.; Wang, W.; Wang, X.; Zhang, B. Highly efficient co-sensitization of nanocrystalline TiO2 electrodes with plural organic dyes. New J. Chem. 2005, 29, 773–776. [Google Scholar] [CrossRef]
- Li, C.; Wang, W.; Wang, X.; Zhang, B.; Cao, Y. Molecular design of squaraine dyes for efficient far-red and near-IR sensitization of solar cells. Chem. Lett. 2005, 34, 554–555. [Google Scholar] [CrossRef]
- Otsuka, A.; Funabiki, K.; Sugiyama, N.; Yoshida, T.; Minoura, H.; Matsui, M. Dye sensitization of ZnO by unsymmetrical squaraine dyes suppressing aggregation. Chem. Lett. 2006, 35, 666–667. [Google Scholar] [CrossRef]
- Burke, A.; Schmidt-Mende, L.; Ito, S.; Grätzel, M. A novel blue dye for near-IR “dye-sensitised” solar cell applications. Chem. Commun. 2007, 234–236. [Google Scholar] [CrossRef] [PubMed]
- Yum, J.-H.; Walter, P.; Huber, S.; Rentsch, D.; Geiger, T.; Nüesch, F.; Angelis, F.D.; Grätzel, M.; Nazeeruddin, M.K. Efficient far red sensitization of nanocrystalline TiO2 films by an unsymmetrical squaraine dye. J. Am. Chem. Soc. 2007, 129, 10320–10321. [Google Scholar] [CrossRef] [PubMed]
- Yum, J.-H.; Moon, S.J.; Humphry-Baker, R.; Walter, P.; Geiger, T.; Nüesch, F.; Grätzel, M.; Nazeeruddin, M.K. Effect of coadsorbent on the photovoltaic performance of squaraine sensitized nanocrystalline solar cells. Nanotechnology 2008, 19, 424005:1–424005:6. [Google Scholar] [CrossRef] [PubMed]
- Aiga, F.; Tada, T. Molecular and electronic structures of black dye; an efficient sensitizing dye for nanocrystalline TiO2 solar cells. J. Mol. Struct. 2003, 658, 25–32. [Google Scholar] [CrossRef]
- Monat, J.E.; Rodriguez, J.H.; McCusker, J.K. Ground- and excited-state electronic structures of the solar cell sensitizer bis(4,4’-dicarboxylato-2,2’ bipyridine)bis(isothiocyanato)ruthenium(II). J. Phys. Chem. A 2002, 106, 7399–7406. [Google Scholar] [CrossRef]
- Fantacci, S.; de Angelis, F.; Selloni, A. Absorption spectrum and solvatochromism of the [Ru(4,4’-COOH-2,2’-bpy)2(NCS)2] molecular dye by time dependent density functional theory. J. Am. Chem. Soc. 2003, 125, 4381–4387. [Google Scholar] [CrossRef] [PubMed]
- Angelis, F.D.; Fantacci, S.; Selloni, A. Time-dependent density functional theory study of the absorption spectrum of [Ru(4,4’-COOH-2,2’-bpy)2(NCS)2] in water solution: Influence of the pH. Chem. Phys. Lett. 2004, 389, 204–208. [Google Scholar] [CrossRef]
- Angelis, F.D.; Fantacci, S.; Selloni, A.; Nazeeruddin, M.K. Time dependent density functional theory study of the absorption spectrum of the [Ru(4,4’-COO−-2,2’-bpy)2(X)2]4−(X = NCS, Cl) dyes in water solution. Chem. Phys. Lett. 2005, 415, 115–120. [Google Scholar] [CrossRef]
- Onozawa-Komatsuzaki, N.; Kitao, O.; Yanagida, M.; Himeda, Y.; Sugihara, H.; Kasuga, K. Molecular and electronic ground and excited structures of heteroleptic ruthenium polypyridyl dyes for nanocrystalline TiO2 solar cells. New J. Chem. 2006, 30, 689–697. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, W.-K.; Cao, M.-J.; Liu, S.-H.; Li, J.-Q.; Philippopoulos, A.I.; Falaras, P. A TD-DFT study on the electronic spectrum of Ru(II)L2 [L = bis(5’-methyl-2,2’-bipyridine-6-carboxylato)] in the gas phase and DMF solution. Chem. Phys. 2006, 330, 204–211. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, J.-J.; Xia, Y.-Y. A comparative theoretical investigation of ruthenium dyes in dye-sensitized solar cells. J. Photochem. Photobiol. A Chem. 2007, 185, 283–288. [Google Scholar] [CrossRef]
- Liu, Z. Theoretical studies of natural pigments relevant to dye-sensitized solar cells. J. Mol. Struct. (Theochem) 2008, 862, 44–48. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, J.-J.; Xia, Y.-Y. Molecular design of coumarin dyes with high efficiency in dye-sensitized solar cells. J. Photochem. Photobiol. A Chem. 2008, 194, 167–172. [Google Scholar] [CrossRef]
- El-Shishtawy, R.M.; Asiri, A.M.; Aziz, S.G.; Elroby, S.A.K. Molecular design of donor-acceptor dyes for efficient dye-sensitized solar cells I: A DFT study. J. Mol. Model. 2014, 20, 2241. [Google Scholar] [CrossRef] [PubMed]
- Srinivas, K.; Prabhakar, C.; Devi, C.L.; Yesudas, K.; Bhanuprakash, K.; Rao, V.J. Enhanced diradical nature in oxyallyl derivatives leads to near infra red absorption: A comparative study of the squaraine and croconate dyes using computational techniques. J. Phys. Chem. A 2007, 111, 3378–3386. [Google Scholar] [CrossRef] [PubMed]
- Gavin Tsai, H.-H.; Tan, C.-J.; Tseng, W.-H. Electron transfer of squaraine-derived dyes adsorbed on TiO2 clusters in dye-sensitized solar cells: A density functional theory investigation. J. Phys. Chem. C 2015, 119, 4431–4443. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, H.; Wang, L.; Liang, G.; Wang, L.; Shen, X.; Xu, W. DFT and TD-DFT studies on symmetrical squaraine dyes for nanocrystalline solar cells. Monatsh. Chem. 2010, 141, 549–555. [Google Scholar] [CrossRef]
- Chung, I.; Lee, B.; He, J.; Chang, R.P.H.; Kanatzidis, M.G. All-solid-state dye-sensitized solar cells with high efficiency. Nature 2012, 485, 486–489. [Google Scholar] [CrossRef] [PubMed]
- Putz, M.V. Compactness aromaticity of atoms in molecules. Int. J. Mol. Sci. 2010, 11, 1269–1310. [Google Scholar] [CrossRef] [PubMed]
- Putz, M.V.; Russo, N.; Sicilia, E. On the applicability of the HSAB principle through the use of improved computational schemes for Chemical Hardness evaluation. J. Comput. Chem. 2004, 25, 994–1003. [Google Scholar] [CrossRef] [PubMed]
- Putz, M.V. Koopmans’ analysis of chemical hardness with spectral-like resolution. MATCH Commun. Math. Comput. Chem. 2010, 64, 391–418. [Google Scholar] [CrossRef] [PubMed]
- Chermette, H. Chemical reactivity indexes in density functional theory. J. Comp. Chem. 1999, 20, 129–154. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09 Suite of Programs; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. IV. A new dynamical correlation functional and implications for exact-exchange mixing. J. Chem. Phys. 1996, 104, 1040–1046. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. V. Systematic optimization of exchange-correlation functionals. J. Chem. Phys. 1997, 107, 8554–8560. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Casida, M.E.; Jamorski, C.; Casida, K.C.; Salahub, D.R. Molecular excitation energies to high-lying bound states from time-dependent density-functional response theory: Characterization and correction of the time-dependent local density approximation ionization threshold. J. Chem. Phys. 1998, 108, 4439–4449. [Google Scholar] [CrossRef]
- Jacquemin, D.; Wathelet, V.; Perpete, E.A.; Adamo, C. Extensive TD-DFT benchmark: Singlet-excited states of organic molecules. J. Chem. Theory Comput. 2009, 5, 2420–2435. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Tao, J.; Staroverov, V.N.; Scuseria, G.E. Metageneralized gradient approximation: Explanation of a realistic nonempirical density functional. J. Chem. Phys. 2004, 120, 6898–6911. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Kurth, S.; Zupan, A.; Blaha, P. Accurate density functional with correct formal properties: A step beyond the generalized gradient approximation. Phys. Rev. Lett. 1999, 82, 2544–2547. [Google Scholar] [CrossRef]
- Wu, J.; Hagelberg, F.; Dinadayalane, T.C.; Leszczynska, D.; Leszczynski, J. Do stone-wales defects alter the magnetic and transport properties of single-walled carbon nanotubes? J. Phys. Chem. C 2011, 115, 22232–22241. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Rohrdanz, M.A.; Martins, K.M.; Herberta, J.M. A long-range-corrected density functional that performs well for both ground-state properties and time-dependent density functional theory excitation energies, including charge-transfer excited states. J. Chem. Phys. 2009, 130, 054112–054118. [Google Scholar] [CrossRef] [PubMed]
- Cossi, M.; Barone, V.; Cammi, R.; Tomasi, J. Ab initio study of solvated molecules: A new implementation of the polarizable continuum model. Chem. Phys. Lett. 1996, 255, 327–335. [Google Scholar] [CrossRef]
- Barone, V.; Cossi, M. Quantum calculation of molecular energies and energy gradients in solution by a conductor solvent model. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]







| Compounds | Wave Length (nm) | Oscillator Strength (f) | MO Contribution | MO Coeff. | EHOMO eV | ELUMO eV | Gap Energy = ELUMO−EHOMO eV |
|---|---|---|---|---|---|---|---|
| SQD1 | 624.86 | 1.416 | HOMO-LUMO | 70% | −4.68 | −3.41 | 1.27 |
| 512.53 | 0.012 | HOMO-1-LUMO | 68% | ||||
| SQD2 | 807.79 | 0.0005 | HOMO-1-LUMO | 70% | −4.50 | −3.19 | 1.31 |
| 600.35 | 1.2269 | HOMO-LUMO | 69% | ||||
| 504.43 | 0.0001 | HOMO-2-LUMO | 68% | ||||
| SQD3 | 864.25 | 0.002 | HOMO-1-LUMO | 70% | −4.47 | −3.38 | 1.09 |
| 692.73 | 0.924 | HOMO-LUMO | 68% | ||||
| 554.05 | 0.324 | HOMO-LUMO+1 | 66% | ||||
| SQD4 | 687 | 1.06 | HOMO-LUMO | 70% | −4.29 | −3.23 | 1.06 |
| 545.92 | 0.00 | HOMO-1.LUMO | 71% |
| Compounds | Tetrahydrofuran | Dichloromethane | Methanol | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cal. | f | Exp. | Dev.EXP | Cal. | f | Exp. | Dev.EXP | Cal. | f | Exp. | Dev.EXP | |
| SQD1 | 652 | 1.81 | 691 | −39 | 642 | 1.74 | 685 | −43 | 655 | 1.77 | 677 | −22 |
| SQD2 | 627 | 1.56 | 679 | −52 | 620 | 1.58 | 677 | −57 | 629 | 1.61 | 668 | −58 |
| SQD3 | 702 | 1.42 | 729 | −27 | 688 | 1.41 | 717 | −29 | 711 | 1.39 | 698 | −13 |
| SQD4 | 705 | 1.23 | 817 | −112 | 695 | 1.06 | 785 | −90 | 705 | 0.92 | 747 | −42 |
| Compounds | χΑΙΜ | ηΑΙΜ | χMOL | ηMOL | AEL | AHard |
|---|---|---|---|---|---|---|
| SQD1 | 6.769 | 5.741 | 0.635 | 8.10 | 10.660 | 0.709 |
| SQD2 | 6.750 | 5.727 | 0.655 | 7.690 | 10.306 | 0.745 |
| SQD3 | 6.735 | 5.703 | 0.545 | 7.850 | 12.359 | 0.726 |
| SQD4 | 6.735 | 5.703 | 0.53 | 7.520 | 12.708 | 0.758 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
El-Shishtawy, R.M.; Elroby, S.A.; Asiri, A.M.; Müllen, K. Optical Absorption Spectra and Electronic Properties of Symmetric and Asymmetric Squaraine Dyes for Use in DSSC Solar Cells: DFT and TD-DFT Studies. Int. J. Mol. Sci. 2016, 17, 487. https://doi.org/10.3390/ijms17040487
El-Shishtawy RM, Elroby SA, Asiri AM, Müllen K. Optical Absorption Spectra and Electronic Properties of Symmetric and Asymmetric Squaraine Dyes for Use in DSSC Solar Cells: DFT and TD-DFT Studies. International Journal of Molecular Sciences. 2016; 17(4):487. https://doi.org/10.3390/ijms17040487
Chicago/Turabian StyleEl-Shishtawy, Reda M., Shaaban A. Elroby, Abdullah M. Asiri, and Klaus Müllen. 2016. "Optical Absorption Spectra and Electronic Properties of Symmetric and Asymmetric Squaraine Dyes for Use in DSSC Solar Cells: DFT and TD-DFT Studies" International Journal of Molecular Sciences 17, no. 4: 487. https://doi.org/10.3390/ijms17040487
APA StyleEl-Shishtawy, R. M., Elroby, S. A., Asiri, A. M., & Müllen, K. (2016). Optical Absorption Spectra and Electronic Properties of Symmetric and Asymmetric Squaraine Dyes for Use in DSSC Solar Cells: DFT and TD-DFT Studies. International Journal of Molecular Sciences, 17(4), 487. https://doi.org/10.3390/ijms17040487