Characterizing the Effects of Washing by Different Detergents on the Wavelength-Scale Microstructures of Silk Samples Using Mueller Matrix Polarimetry
Abstract
:1. Introduction
2. Results and Discussion
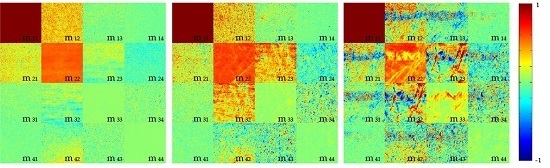
2.1. 2D Images of Mueller Matrix Elements
2.2. Frequency Distribution Histogram (FDH) of Mueller Matrix Elements
2.3. Mueller Matrix Parameters of Silk Sample Based on FDHs
2.4. Wavelength-Scale Microstructural Variations of Silk Samples
2.5. Monte Carlo Simulations
2.6. Results of X-ray Diffraction and Discussions
3. Materials and Methods
3.1. Experimental Setup and Silk Samples
3.2. Frequency Distribution Histograms (FDHs) and Quantitative Parameters
3.3. Monte Carlo (MC) Simulation
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Santin, M.; Motta, A.; Freddi, G.; Cannas, M. In vitro evaluation of the inflammatory potential of the silk fibroin. J. Biomed. Mater. Res. 1999, 46, 382–389. [Google Scholar] [CrossRef]
- Acharya, C.; Kumar, V.; Sen, R.; Kundu, S.C. Performance evaluation of a silk protein based matrix for the enzymatic conversion of tyrosine to L-DOPA. Biotechnol. J. 2008, 3, 226–233. [Google Scholar] [CrossRef] [PubMed]
- Meinel, L.; Fajardo, R.; Hofmann, S.; Langer, R. Silk implants for the healing of critical size bone defects. Bone 2005, 37, 688–698. [Google Scholar] [CrossRef] [PubMed]
- Chitrangada, A.; Boris, H.; Subhas, C.K. The effect of lactose-conjugated silk biomaterials on the development of fibrogenic fibroblasts. Biomaterials 2008, 29, 4665–4675. [Google Scholar]
- Cao, Y.; Wang, B.C. Biodegradation of silk biomaterials. Int. J. Mol. Sci. 2009, 10, 1514–1524. [Google Scholar] [CrossRef] [PubMed]
- Heslot, H. Arfificial fibrous proteins: A review. Biochimie 1998, 80, 9–13. [Google Scholar] [CrossRef]
- Chitrangada, A.; Sudip, K.G.; Kundu, S.C. Silk fibroin film from non-mulberry tropical tasar silkworms: A novel substrate for in vitro fibroblast culture. Acta Biomater. 2009, 5, 429–437. [Google Scholar]
- Zhou, C.Z.; Confalonieri, F.; Medina, N.; Zivanovic, Y.; Esnault, C.; Yang, T.; Jacquet, M.; Janin, J.; Duguet, M.; Perasso, R.; et al. Fine organization of B. mori fibroin heavy chain gene. Nucleic Acids Res. 2000, 28, 2413–2419. [Google Scholar] [CrossRef] [PubMed]
- Zhou, P.; Xie, X. Effects of pH and calcium ions on the conformational transitions in silk fibroin using 2D raman correlation spectroscopy and 13C solid-state NMR. Biochemistry 2004, 43, 11302–11311. [Google Scholar] [CrossRef] [PubMed]
- Hino, T.; Tanimoto, M.; Shimabayashi, S. Change in secondary structure of silk fibroin during preparation of its microspheres by spray-drying and exposure to humid atmosphere. J. Colloid Interface Sci. 2003, 266, 68–73. [Google Scholar] [CrossRef]
- Alali, S.; Vitkin, I.A. Polarized light imaging in biomedicine: Emerging Mueller matrix methodologies for bulk tissue assessment. J. Biomed. Opt. 2015. [Google Scholar] [CrossRef] [PubMed]
- He, H.; Sun, M.; Zeng, N.; Du, E.; Liu, S.; Guo, Y.; Wu, J.; He, Y.; Ma, H. Mapping local orientation of aligned fibrous scatterers for cancerous tissues using backscattering Mueller matrix imaging. J. Biomed. Opt. 2014. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, N.; Vitkin, I.A. Tissue polarimetry: Concepts, challenges, applications, and outlook. J. Biomed. Opt. 2011. [Google Scholar] [CrossRef] [PubMed]
- Ye, H.; Xu, J.; Freudenthal, J.; Kahr, B. On the circular birefringence of polycrystalline polymers: Polylactide. J. Am. Chem. Soc. 2011, 133, 13848–13851. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Du, W.; Chen, X.; Jiang, H.; Zhang, C. Mueller matrix imaging ellipsometry for nanostructure metrology. Opt. Express 2015, 23, 17316–17329. [Google Scholar] [CrossRef] [PubMed]
- Snik, F.; Jones, J.C.; Escuti, M.; Fineschi, S.; Harrington, D.; Martino, A.D.; Mawet, D.; Riedi, J.; Tyo, J.S. An overview of polarimetric sensing techniques and technology with applications to different research fields. Proc. SPIE 2014. [Google Scholar] [CrossRef]
- Wang, Y.; He, H.; Chang, J.; Zeng, N.; Liu, S.; Li, M.; Ma, H. Differentiating characteristic microstructural features of canceroustissues using Mueller matrix microscope. Micron 2015, 79, 8–15. [Google Scholar] [CrossRef] [PubMed]
- Sun, M.; He, H.; Zeng, N.; Du, E.; Guo, Y.; Peng, C.; He, Y.; Ma, H. Probing microstructural information of anisotropic scattering media using rotation-independent polarization parameters. Appl. Opt. 2014, 53, 2949–2955. [Google Scholar] [CrossRef] [PubMed]
- Du, E.; He, H.; Zeng, N.; Sun, M.; Guo, Y.; Wu, J.; Liu, S.; Ma, H. Mueller matrix polarimetry for differentiating characteristic features of cancerous tissues. J. Biomed. Opt. 2014. [Google Scholar] [CrossRef] [PubMed]
- Sun, M.; He, H.; Zeng, N.; Du, E.; Guo, Y.; Liu, S.; Wu, J.; He, Y.; Ma, H. Characterizing the microstructures of biological tissues using Mueller matrix and transformed polarization parameters. Biomed. Opt. Express 2014, 5, 4223–4234. [Google Scholar] [CrossRef] [PubMed]
- Pierangelo, A.; Manhas, S.; Benali, A.; Fallet, C.; Totobenazara, J.; Antonelli, M.; Novikova, T.; Gayet, B.; Martino, A.D.; Validire, P. Multispectral Mueller polarimetric imaging detecting residual cancer and cancer regression after neoadjuvant treatment for colorectal carcinomas. J. Biomed. Opt. 2013. [Google Scholar] [CrossRef] [PubMed]
- Dubreuil, M.; Babilotte, P.; Martin, L.; Sevrain, D.; Rivet, S.; Grand, Y.L.; Brun, G.L.; Turlin, B.; Jeune, B.L. Mueller matrix polarimetry for improved liver fibrosis diagnosis. Opt. Lett. 2012, 37, 1061–1063. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Lim, L.G.; Srivastava, S.; Yan, J.S.; Shabbir, A.; Liu, Q. Roles of linear and circular polarization properties and effect of wavelength choice on differentiation between ex vivo normal and cancerous gastric samples. J. Biomed. Opt. 2014. [Google Scholar] [CrossRef] [PubMed]
- Jagtap, J.; Chandel, S.; Das, N.; Soni, J.; Chatterjee, S.; Pradhan, A.; Ghosh, N. Quantitative Mueller matrix fluorescence spectroscopy for precancer detection. Opt. Lett. 2014, 39, 243–246. [Google Scholar] [CrossRef] [PubMed]
- He, H.; Zeng, N.; Liao, R.; Yun, T.; Li, W.; He, Y.; Ma, H. Application of sphere-cylinder scattering model to skeletal muscle. Opt. Express 2010, 18, 15104–15112. [Google Scholar] [CrossRef] [PubMed]
- He, C.; He, H.; Li, X.; Chang, J.; Wang, Y.; Liu, S.; Zeng, N.; He, Y.; Ma, H. Quantitatively differentiating microstructures of tissues by frequency distributions of Mueller matrix images. J. Biomed. Opt. 2015. [Google Scholar] [CrossRef] [PubMed]
- Yun, T.; Zeng, N.; Li, W.; Li, D.; Jiang, X.; Ma, H. Monte Carlo simulation of polarized photon scattering in anisotropic media. Opt. Express 2009, 17, 16591–16602. [Google Scholar] [CrossRef] [PubMed]
- Harris, J.I.; Cole, R.D.; Pon, N.G. The kinetics of acid hydrolysis of dipeptides. J. Biochem. 1956, 62, 154–159. [Google Scholar] [CrossRef]
- Byler, D.M.; Susi, H. Examination of the secondary structure of proteins by deconvolved. Biopolymers 1986, 25, 469–487. [Google Scholar] [CrossRef] [PubMed]
- Azzam, R.M.A. Photopolarimetric measurement of the Mueller matrix by Fourier analysis of a single detected signal. Opt. Lett. 1978, 2, 148–150. [Google Scholar] [CrossRef]
- Chenuault, D.B.; Pezzaniti, J.L.; Chipman, R.A. Mueller matrix algorithms. Proc. SPIE 1992, 1746, 231–246. [Google Scholar]
- He, H.; Chang, J.; He, C.; Ma, H. Transformation of full 4 × 4 Mueller matrices: A quantitative technique for biomedical diagnosis. Proc. SPIE 2016. [Google Scholar] [CrossRef]










| Detergent/Parameter | m12 | m22 | m23 | m32 | m33 |
|---|---|---|---|---|---|
| F/P1_0 | 0.030 | 0.536 | 0.013 | 0.008 | 0.039 |
| F/P1_1 | 0.029 | 0.504 | 0.036 | 0.030 | 0.043 |
| F/P1_2 | 0.028 | 0.492 | −0.003 | −0.005 | 0.042 |
| F/P1_3 | 0.029 | 0.526 | 0.009 | 0.002 | 0.048 |
| F/P1_4 | 0.030 | 0.510 | 0.029 | 0.023 | 0.045 |
| F/P1_5 | 0.029 | 0.524 | 0.015 | 0.009 | 0.048 |
| F/P1_6 | 0.024 | 0.485 | −0.012 | −0.030 | 0.042 |
| F/P2_0 | 0.011 | 0.022 | 0.018 | 0.022 | 0.016 |
| F/P2_1 | 0.012 | 0.021 | 0.019 | 0.023 | 0.016 |
| F/P2_2 | 0.011 | 0.022 | 0.019 | 0.022 | 0.016 |
| F/P2_3 | 0.012 | 0.023 | 0.020 | 0.023 | 0.017 |
| F/P2_4 | 0.011 | 0.022 | 0.019 | 0.023 | 0.017 |
| F/P2_5 | 0.012 | 0.022 | 0.019 | 0.024 | 0.017 |
| F/P2_6 | 0.011 | 0.022 | 0.018 | 0.022 | 0.016 |
| Detergent/Parameter | m12 | m22 | m23 | m32 | m33 |
|---|---|---|---|---|---|
| L/P1_0 | 0.032 | 0.528 | 0.075 | 0.071 | 0.049 |
| L/P1_1 | 0.029 | 0.552 | 0.019 | 0.010 | 0.046 |
| L/P1_2 | 0.027 | 0.534 | 0.037 | 0.036 | 0.051 |
| L/P1_3 | 0.030 | 0.515 | 0.044 | 0.038 | 0.053 |
| L/P1_4 | 0.032 | 0.512 | 0.056 | 0.050 | 0.056 |
| L/P1_5 | 0.034 | 0.522 | 0.019 | 0.013 | 0.049 |
| L/P1_6 | 0.032 | 0.482 | 0.004 | −0.002 | 0.044 |
| L/P2_0 | 0.012 | 0.019 | 0.023 | 0.027 | 0.018 |
| L/P2_1 | 0.012 | 0.018 | 0.023 | 0.027 | 0.018 |
| L/P2_2 | 0.012 | 0.018 | 0.022 | 0.026 | 0.018 |
| L/P2_3 | 0.012 | 0.018 | 0.022 | 0.026 | 0.019 |
| L/P2_4 | 0.012 | 0.019 | 0.022 | 0.026 | 0.019 |
| L/P2_5 | 0.013 | 0.019 | 0.023 | 0.027 | 0.019 |
| L/P2_6 | 0.012 | 0.019 | 0.022 | 0.026 | 0.018 |
| Detergent/Parameter | m12 | m22 | m23 | m32 | m33 |
|---|---|---|---|---|---|
| T/P1_0 | 0.033 | 0.560 | 0.001 | −0.006 | 0.039 |
| T/P1_1 | 0.039 | 0.492 | 0.006 | −0.001 | 0.047 |
| T/P1_2 | 0.039 | 0.453 | −0.016 | −0.023 | 0.052 |
| T/P1_3 | 0.037 | 0.418 | −0.004 | −0.006 | 0.061 |
| T/P1_4 | 0.033 | 0.379 | 0.003 | −0.002 | 0.057 |
| T/P1_5 | 0.031 | 0.367 | 0.004 | −0.003 | 0.061 |
| T/P1_6 | 0.026 | 0.307 | −0.016 | −0.021 | 0.061 |
| T/P2_0 | 0.013 | 0.024 | 0.020 | 0.023 | 0.019 |
| T/P2_1 | 0.013 | 0.025 | 0.021 | 0.023 | 0.019 |
| T/P2_2 | 0.013 | 0.029 | 0.019 | 0.021 | 0.019 |
| T/P2_3 | 0.013 | 0.028 | 0.020 | 0.021 | 0.019 |
| T/P2_4 | 0.012 | 0.031 | 0.019 | 0.020 | 0.019 |
| T/P2_5 | 0.012 | 0.027 | 0.019 | 0.020 | 0.019 |
| T/P2_6 | 0.011 | 0.027 | 0.018 | 0.018 | 0.018 |
| Detergent/Parameter | m12 | m22 | m23 | m32 | m33 |
|---|---|---|---|---|---|
| C/P1_0 | 0.034 | 0.555 | 0.009 | 0.002 | 0.034 |
| C/P1_1 | 0.036 | 0.582 | 0.134 | 0.131 | 0.060 |
| C/P1_2 | 0.039 | 0.636 | 0.073 | 0.067 | 0.042 |
| C/P1_3 | 0.032 | 0.607 | 0.074 | 0.067 | 0.047 |
| C/P1_4 | 0.030 | 0.585 | 0.017 | 0.006 | 0.061 |
| C/P1_5 | 0.025 | 0.560 | −0.010 | −0.019 | 0.113 |
| C/P1_6 | 0.010 | 0.441 | 0.003 | −0.009 | 0.182 |
| C/P2_0 | 0.013 | 0.024 | 0.020 | 0.022 | 0.018 |
| C/P2_1 | 0.014 | 0.024 | 0.021 | 0.025 | 0.022 |
| C/P2_2 | 0.017 | 0.029 | 0.027 | 0.029 | 0.027 |
| C/P2_3 | 0.018 | 0.032 | 0.029 | 0.030 | 0.030 |
| C/P2_4 | 0.019 | 0.040 | 0.031 | 0.034 | 0.036 |
| C/P2_5 | 0.029 | 0.073 | 0.061 | 0.066 | 0.079 |
| C/P2_6 | 0.032 | 0.107 | 0.073 | 0.078 | 0.119 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Y.; He, H.; He, C.; Zhou, J.; Zeng, N.; Ma, H. Characterizing the Effects of Washing by Different Detergents on the Wavelength-Scale Microstructures of Silk Samples Using Mueller Matrix Polarimetry. Int. J. Mol. Sci. 2016, 17, 1301. https://doi.org/10.3390/ijms17081301
Dong Y, He H, He C, Zhou J, Zeng N, Ma H. Characterizing the Effects of Washing by Different Detergents on the Wavelength-Scale Microstructures of Silk Samples Using Mueller Matrix Polarimetry. International Journal of Molecular Sciences. 2016; 17(8):1301. https://doi.org/10.3390/ijms17081301
Chicago/Turabian StyleDong, Yang, Honghui He, Chao He, Jialing Zhou, Nan Zeng, and Hui Ma. 2016. "Characterizing the Effects of Washing by Different Detergents on the Wavelength-Scale Microstructures of Silk Samples Using Mueller Matrix Polarimetry" International Journal of Molecular Sciences 17, no. 8: 1301. https://doi.org/10.3390/ijms17081301
APA StyleDong, Y., He, H., He, C., Zhou, J., Zeng, N., & Ma, H. (2016). Characterizing the Effects of Washing by Different Detergents on the Wavelength-Scale Microstructures of Silk Samples Using Mueller Matrix Polarimetry. International Journal of Molecular Sciences, 17(8), 1301. https://doi.org/10.3390/ijms17081301