Deciphering Molecular Mechanisms of Interface Buildup and Stability in Porous Si/Eumelanin Hybrids
Abstract
:1. Introduction
2. Results and Discussion
2.1. Temporal Stability of the Eumelanin-PSi Hybrids
2.2. Effect of Surface Modifications on the Temporal Stability of the Photocurrents
2.2.1. Effect of PSi Surface Oxidation
2.2.2. Effect of the Use of a DHI and DHICA Mixture for the Impregnation
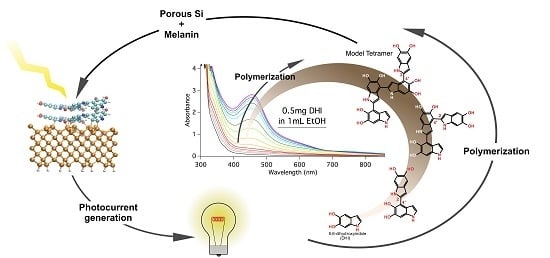
2.3. Oxidation of DHI in Ethanol Solution
2.4. Formation and Stacking Energies
2.5. Calculation of the Tetramer Optical Absorption
2.6. Adhesion Energy
3. Materials and Methods
3.1. PSi–Eumelanin Hybrid Preparation
3.2. Formation and Stacking Energies Calculations
3.3. Optical Spectra Calculation
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| PSi | Porous silicon |
| DHI | 5,6-Dihydroxyindole |
| DHICA | 5,6-Dihydroxyindole-2-carboxylic acid |
| DFT | Density Functional Theory |
| TD-DFT | Time-dependent DFT |
| EtOH | Ethanol |
| AISSP | Ammonia-induced solid state polymerization |
| SEM-EDS | Scanning Electron Microscopy—Energy Dispersive Spectroscopy |
References
- Judeinstein, P.; Sanchez, C. Hybrid organic/inorganic materials: A land of multidisciplinarity. J. Mater. Chem. 1996, 6, 511. [Google Scholar] [CrossRef]
- Wang, S.; Kang, Y.; Wang, L.; Zhang, H.; Wang, Y.; Wang, Y. Organic/inorganic hybrid sensors: A review. Sens. Actuators B Chem. 2013, 182, 467–481. [Google Scholar] [CrossRef]
- Lin, C.-F.; Su, W.-F.; Wu, C.-I.; Cheng, I.-C. Organic, Inorganic and Hybrid Solar Cells: Principles and Practice, 1st ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 2012. [Google Scholar]
- Napolitano, A.; Ball, V.; Chen, C.; Buehler, M.J. Polydopamine and Eumelanin: From Structure–Property Relationships to a Unified Tailoring Strategy. Acc. Chem. Res. 2014, 47, 3541–3550. [Google Scholar] [CrossRef]
- Liebscher, J.; Mrówczyński, R.; Scheidt, H.A.; Filip, C.; Haìdade, N.D.; Turcu, R.; Bende, A.; Beck, S. Structure of polydopamine: A never-ending story? Langmuir 2013, 29, 10539–10548. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.; Chen, C.-T.; Bdikin, I.; Ball, V.; Grácio, J.; Buehler, M.J. Tuning heterogeneous poly(dopamine) structures and mechanics: In silico covalent cross-linking and thin film nanoindentation. Soft Matter 2014, 10, 457–464. [Google Scholar] [CrossRef] [PubMed]
- Nofsinger, J.B.; Forest, S.E.; Simon, J.D. Explanation for the Disparity among Absorption and Action Spectra of Eumelanin. J. Phys. Chem. B 1999, 103, 11428–11432. [Google Scholar] [CrossRef]
- Brian Nofsinger, J.; Simon, J.D. Radiative Relaxation of Sepia Eumelanin is Affected by Aggregation? Photochem. Photobiol. 2007, 74, 31–37. [Google Scholar] [CrossRef]
- Tran, M.L.; Powell, B.J.; Meredith, P. Chemical and structural disorder in eumelanins: A possible explanation for broadband absorbance. Biophys. J. 2006, 90, 743–752. [Google Scholar] [CrossRef] [PubMed]
- Ou-Yang, H.; Stamatas, G.; Kollias, N. Spectral Responses of Melanin to Ultraviolet A Irradiation. J. Investig. Dermatol. 2004, 122, 492–496. [Google Scholar] [CrossRef] [PubMed]
- Mula, G.; Manca, L.; Setzu, S.; Pezzella, A. Photovoltaic properties of PSi impregnated with eumelanin. Nanoscale Res. Lett. 2012, 7, 377. [Google Scholar] [CrossRef] [PubMed]
- Pinna, A.; Simbula, F.; Marongiu, D.; Pezzella, A.; d’Ischia, M.; Mula, G. Boosting, probing and switching-off visible light-induced photocurrents in eumelanin-porous silicon hybrids. RSC Adv. 2015, 5, 56704–56710. [Google Scholar] [CrossRef]
- Meredith, P.; Sarna, T. The physical and chemical properties of eumelanin. Pigment Cell Res. 2006, 19, 572–594. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.-T.; Chuang, C.; Cao, J.; Ball, V.; Ruch, D.; Buehler, M.J. Excitonic effects from geometric order and disorder explain broadband optical absorption in eumelanin. Nat. Commun. 2014, 5, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.-T.; Martin-Martinez, F.J.; Jung, G.S.; Buehler, M.J. Polydopamine and eumelanin molecular structures investigated with ab initio calculations. Chem. Sci. 2017, 8, 1631–1641. [Google Scholar] [CrossRef] [PubMed]
- Micillo, R.; Panzella, L.; Iacomino, M.; Prampolini, G.; Cacelli, I.; Ferretti, A.; Crescenzi, O.; Koike, K.; Napolitano, A.; d’Ischia, M. Eumelanin broadband absorption develops from aggregation-modulated chromophore interactions under structural and redox control. Sci. Rep. 2017, 7, 41532. [Google Scholar] [CrossRef] [PubMed]
- D’Ischia, M.; Crescenzi, O.; Pezzella, A.; Arzillo, M.; Panzella, L.; Napolitano, A.; Barone, V. Structural effects on the electronic absorption properties of 5,6-dihydroxyindole oligomers: The potential of an integrated experimental and DFT approach to model eumelanin optical properties. Photochem. Photobiol. 2008, 84, 600–607. [Google Scholar] [CrossRef] [PubMed]
- Pezzella, A.; Panzella, L.; Crescenzi, O.; Napolitano, A.; Navaratnam, S.; Edge, R.; Land, E.J.; Barone, V.; D’Ischia, M. Lack of visible chromophore development in the pulse radiolysis oxidation of 5,6-dihydroxyindole-2-carboxylic acid oligomers: DFT investigation and implications for eumelanin absorption properties. J. Org. Chem. 2009, 74, 3727–3734. [Google Scholar] [CrossRef] [PubMed]
- d’Ischia, M.; Napolitano, A.; Pezzella, A.; Meredith, P.; Sarna, T. Chemical and structural diversity in eumelanins: Unexplored bio-optoelectronic materials. Angew. Chem. Int. Ed. Engl. 2009, 48, 3914–3921. [Google Scholar] [CrossRef] [PubMed]
- Pezzella, A.; Barra, M.; Musto, A.; Navarra, A.; Alfè, M.; Manini, P.; Parisi, S.; Cassinese, A.; Criscuolo, V.; d’Ischia, M. Stem cell-compatible eumelanin biointerface fabricated by chemically controlled solid state polymerization. Mater. Horiz. 2015, 2, 212–220. [Google Scholar] [CrossRef]
- Chen, C.-T.; Ball, V.; de Almeida Gracio, J.J.; Singh, M.K.; Toniazzo, V.; Ruch, D.; Buehler, M.J. Self-Assembly of Tetramers of 5,6-Dihydroxyindole Explains the Primary Physical Properties of Eumelanin: Experiment, Simulation, and Design. ACS Nano 2013, 7, 1524–1532. [Google Scholar] [CrossRef] [PubMed]
- Arzillo, M.; Mangiapia, G.; Pezzella, A.; Heenan, R.K.; Radulescu, A.; Paduano, L.; D’Ischia, M. Eumelanin buildup on the nanoscale: Aggregate growth/assembly and visible absorption development in biomimetic 5,6-dihydroxyindole polymerization. Biomacromolecules 2012, 13, 2379–2390. [Google Scholar] [CrossRef] [PubMed]
- Theiss, W.; Arntzen, M.; Hilbrich, S.; Wernke, M.; Arens-Fischer, R.; Bercer, M.G.; Arens-Fisher, R.; Berger, M.G. From Minutes To Months—Aging of Porous Silicon Single Layers and Superlattices. Phys. Status Solidi B Basic Res. 1995, 190, 15–20. [Google Scholar] [CrossRef]
- Karacali, T.; Cakmak, B.; Efeoglu, H. Aging of porous silicon and the origin of blue shift. Opt. Express 2003, 11, 1237–1242. [Google Scholar] [CrossRef] [PubMed]
- Aggarwal, G.; Mishra, P.; Joshi, B.; Harsh; Islam, S.S. Porous silicon surface stability: A comparative study of thermal oxidation techniques. J. Porous Mater. 2014, 21, 23–29. [Google Scholar] [CrossRef]
- Bimbo, L.M.; Sarparanta, M.; Santos, H.A.; Airaksinen, A.J.; Mäkilä, E.; Laaksonen, T.; Peltonen, L.; Lehto, V.-P.; Hirvonen, J.; Salonen, J. Biocompatibility of thermally hydrocarbonized porous silicon nanoparticles and their biodistribution in rats. ACS Nano 2010, 4, 3023–3032. [Google Scholar] [CrossRef] [PubMed]
- Lees, I.N.; Lin, H.; Canaria, C.A.; Gurtner, C.; Sailor, M.J.; Miskelly, G.M. Chemical Stability of Porous Silicon Surfaces Electrochemically Modified with Functional Alkyl Species. Langmuir 2003, 19, 9812–9817. [Google Scholar] [CrossRef]
- Tiddia, M.; Mula, G.; Sechi, E.; Vacca, A.; Cara, E.; De Leo, N.; Fretto, M.; Boarino, L. 4-Nitrobenzene Grafted in Porous Silicon: Application to Optical Lithography. Nanoscale Res. Lett. 2016, 11, 436. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mula, G.; Pinna, E.; Melis, C.; Colombo, L.; Prontera, C.T.; Pezzella, A.; D’Ischia, M. Eumelanin-Porous Silicon Hybrids: Towards Stable Photocurrents. In Extended Abstracts of the 10th International Conference of Porous Semiconductors—Science and Technology 2016; Canham, L.T., Sailor, M.J., Cantarero, A., Koshida, N., Barillaro, G., Djenizian, T., Marsal, L., Eds.; Lifelong Learning Center of the Rovira I Virgili University Foundation: Tarragona, Spain, 2016; pp. 234–235. [Google Scholar]
- Orazem, M.E.; Tribollet, B. Electrochemical Impedance Spectroscopy; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2008. [Google Scholar]
- Jo, S.B.; Lee, J.H.; Sim, M.; Kim, M.; Park, J.H.; Choi, Y.S.; Kim, Y.; Ihn, S.-G.; Cho, K. High Performance Organic Photovoltaic Cells Using Polymer-Hybridized ZnO Nanocrystals as a Cathode Interlayer. Adv. Energy Mater. 2011, 1, 690–698. [Google Scholar] [CrossRef]
- He, J.; Gao, P.; Ling, Z.; Ding, L.; Yang, Z.; Ye, J.; Cui, Y. High-Efficiency Silicon/Organic Heterojunction Solar Cells with Improved Junction Quality and Interface Passivation. ACS Nano 2016, 10, 11525–11531. [Google Scholar] [CrossRef] [PubMed]
- Sheng, J.; Fan, K.; Wang, D.; Han, C.; Fang, J.; Gao, P.; Ye, J. Improvement of the SiOx Passivation Layer for High-Efficiency Si/PEDOT:PSS Heterojunction Solar Cells. ACS Appl. Mater. Interfaces 2014, 6, 16027–16034. [Google Scholar] [CrossRef] [PubMed]
- Jia, Y.; Cao, A.; Kang, F.; Li, P.; Gui, X.; Zhang, L.; Shi, E.; Wei, J.; Wang, K.; Zhu, H.; Wu, D. Strong and reversible modulation of carbon nanotube–silicon heterojunction solar cells by an interfacial oxide layer. Phys. Chem. Chem. Phys. 2012, 14, 8391. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Kozawa, D.; Miyauchi, Y.; Hiraoka, K.; Mouri, S.; Ohno, Y.; Matsuda, K. Considerably improved photovoltaic performance of carbon nanotube-based solar cells using metal oxide layers. Nat. Commun. 2015, 6, 6305. [Google Scholar] [CrossRef] [PubMed]
- Mula, G.; Tiddia, M.V.; Ruffilli, R.; Falqui, A.; Palmas, S.; Mascia, M.; Ruffilli, R.; Falqui, A.; Palmas, S.; Mascia, M. Electrochemical impedance spectroscopy of oxidized porous silicon. Thin Solid Films 2014, 556, 311–316. [Google Scholar] [CrossRef]
- Matta, S.K.; Kakiage, K.; Makuta, S.; Veamatahau, A.; Aoyama, Y.; Yano, T.; Hanaya, M.; Tachibana, Y. Dye-Anchoring Functional Groups on the Performance of Dye-Sensitized Solar Cells: Comparison between Alkoxysilyl and Carboxyl Groups. J. Phys. Chem. C 2014, 118, 28425–28434. [Google Scholar] [CrossRef]
- Mian, S.A.; Saha, L.C.; Jang, J.; Wang, L.; Gao, X.; Nagase, S. Density Functional Theory Study of Catechol Adhesion on Silica Surfaces. J. Phys. Chem. C 2010, 114, 20793–20800. [Google Scholar] [CrossRef]
- Meredith, P.; Powell, B.J.; Riesz, J.; Nighswander-Rempel, S.P.; Pederson, M.R.; Moore, E.G. Towards structure–property–function relationships for eumelanin. Soft Matter 2006, 2, 37. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Perdew, Burke, and Ernzerhof Reply. Phys. Rev. Lett. 1998, 80, 891. [Google Scholar] [CrossRef]
- Antidormi, A.; Melis, C.; Canadell, E.; Colombo, L. Assessing the Performance of Eumelanin/Si Interface for Photovoltaic Applications. J. Phys. Chem. C 2017. [Google Scholar] [CrossRef]
- Kaxiras, E.; Tsolakidis, A.; Zonios, G.; Meng, S. Structural model of eumelanin. Phys. Rev. Lett. 2006, 97, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Meng, S.; Kaxiras, E. Theoretical Models of Eumelanin Protomolecule and Its Photoprotection Mechanism. Biophys. J. 2009, 96, 300a. [Google Scholar] [CrossRef]
- Soler, J.M.; Artacho, E.; Gale, J.D.; Garcia, A.; Junquera, J.; Ordejon, P.; Sanchez-Portal, D. The SIESTA method for ab initio order-N materials simulation. J. Phys. 2001. [Google Scholar] [CrossRef]
- Cappellini, G.; Malloci, G.; Mulas, G. Electronic excitations of oligoacenes: A time dependent density functional theory study. Superlattices Microstruct. 2009, 46, 14–18. [Google Scholar] [CrossRef]
- Panzella, L.; Pezzella, A.; Napolitano, A.; D’Ischia, M. The first 5,6-dihydroxyindole tetramer by oxidation of 5,5′,6, 6′-tetrahydroxy-2,4′-biindolyl and an unexpected issue of positional reactivity en route to eumelanin-related polymers. Org. Lett. 2007, 9, 1411–1414. [Google Scholar] [CrossRef] [PubMed]
- Panzella, L.; Gentile, G.; D’Errico, G.; Della Vecchia, N.F.; Errico, M.E.; Napolitano, A.; Carfagna, C.; d’Ischia, M. Atypical Structural and π-Electron Features of a Melanin Polymer That Lead to Superior Free-Radical-Scavenging Properties. Angew. Chem. Int. Ed. 2013, 52, 12684–12687. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. Quantum ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892–7895. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Barone, V.; Casarin, M.; Forrer, D.; Pavone, M.; Sambi, M.; Vittadini, A. Role and effective treatment of dispersive forces in materials: Polyethylene and graphite crystals as test cases. J. Comput. Chem. 2009, 30, 934–939. [Google Scholar] [CrossRef] [PubMed]
- Andreussi, O.; Dabo, I.; Marzari, N. Revised self-consistent continuum solvation in electronic-structure calculations. J. Chem. Phys. 2012, 136. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Kohn, W. Nobel Lecture: Electronic structure of matter—Wave functions and density functionals. Rev. Mod. Phys. 1999, 71, 1253–1266. [Google Scholar] [CrossRef]
- Jones, R.O.; Gunnarsson, O. The density functional formalism, its applications and prospects. Rev. Mod. Phys. 1989, 61, 689–746. [Google Scholar] [CrossRef]
- Marques, M.A.L.; Gross, E.K.U. Time-Dependent Density Functional Theory. Annu. Rev. Phys. Chem. 2004, 55, 427–455. [Google Scholar] [CrossRef] [PubMed]
- Valiev, M.; Bylaska, E.J.; Govind, N.; Kowalski, K.; Straatsma, T.P.; Van Dam, H.J.J.; Wang, D.; Nieplocha, J.; Apra, E.; Windus, T.L.; et al. NWChem: A comprehensive and scalable open-source solution for large scale molecular simulations. Comput. Phys. Commun. 2010, 181, 1477–1489. [Google Scholar] [CrossRef]
- Valiev, M.; Bylaska, E.J.; Govind, N.; Kowalski, K.; Straatsma, T.P.; van Dam, H.J.J.; Wang, D.; Nieplocha, J.; Apra, E.; Windus, T.L.; et al. NWChem: Open Source High-Performance Computational Chemistry. Available online: http://www.nwchem-sw.org/index.php/Main_Page (accessed on 18 July 2017).
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Grimme, S.; Parac, M. Substantial Errors from Time-Dependent Density Functional Theory for the Calculation of Excited States of Large π Systems. ChemPhysChem 2003, 4, 292–295. [Google Scholar] [CrossRef] [PubMed]
- Casida, M.E. Time-Dependent Density Functional Response Theory for Molecules. In Recent Advances in Density Functional Theory. Vol. I.; Chong, D.P., Ed.; World Scientific: Singapore, 1995; pp. 155–192. [Google Scholar]
- Cardia, R.; Malloci, G.; Mattoni, A.; Cappellini, G. Effects of TIPS-functionalization and perhalogenation on the electronic, optical, and transport properties of angular and compact dibenzochrysene. J. Phys. Chem. A 2014, 118, 5170–5177. [Google Scholar] [CrossRef] [PubMed]
- Malloci, G.; Cappellini, G.; Mulas, G.; Satta, G. Quasiparticle effects and optical absorption in small fullerenelike GaP clusters. Phys. Rev. B Condens. Matter Mater. Phys. 2004, 70, 1–6. [Google Scholar] [CrossRef]
- Cardia, R.; Cappellini, G.; Pinna, E.; Tiddia, M.V.; Mula, G. Optical and Electronic Properties of Monomers of Eumelanin: A DFT and TD-DFT Computational Study. Opt. Photonics J. 2016, 6, 41–47. [Google Scholar] [CrossRef]
- Cooke, M.V.; Malvacio, I.; Peláez, W.J.; Pepino, A.J.; Mazzieri, M.R.; Argüello, G.A. TD-DFT calculations of UV absorption bands and their intensities in the spectra of some tetrahydroquinolines. RSC Adv. 2015, 5, 26255–26262. [Google Scholar] [CrossRef]












| Formation Energy (eV) | Vacuum | Methanol | Water |
|---|---|---|---|
| Model 1-a (one C=O) | −0.56 | −0.12 | 0.67 |
| Model 1-b (two C=O) | −0.26 | 0.35 | 0.74 |
| Model 1-c (four C=O) | −1.20 | −0.07 | 0.92 |
| Model 1-d (six C=O) | −1.46 | −0.20 | 0.91 |
| Stacking Energy (eV) | Vacuum | Methanol | Water |
|---|---|---|---|
| Model 1-a (one =O) | −1.52 | −1.08 | −0.89 |
| Model 1-b (two =O) | −1.22 | −1.01 | −0.78 |
| Model 1-c (four =O) | −1.75 | −1.22 | −0.88 |
| Model 1-d (six =O) | −2.01 | −1.76 | −1.21 |
| PT | C | Onset | 1086 nm (1.14 eV) | HOMO → LUMO |
| B | 1st Peak in Range | 800 nm (1.55 eV) | HOMO − 2 → LUMO | |
| HOMO − 2 → LUMO + 1 | ||||
| A | Maximum Peak | 410 nm (3.02 eV) | HOMO − 6 → LUMO + 2 | |
| HOMO − 6 → LUMO + 1 | ||||
| HOMO − 3 → LUMO + 1 | ||||
| HOMO − 2 → LUMO + 3 | ||||
| Model 1-d | C | Onset | 1563 nm (0.79 eV) | HOMO → LUMO |
| B | 1st Peak in Range | 690 nm (1.80 eV) | HOMO − 1 → LUMO + 1 | |
| A | Maximum Peak | 367 nm (3.38 eV) | HOMO → LUMO + 4 |
| N. | Exp. (nm) | Model 1-d (nm) | PT (nm) | N. | Exp. (nm) | Model 1-d (nm) | PT (nm) |
|---|---|---|---|---|---|---|---|
| 1 | 210 (LM) | 217 (LM) | 213 (LM) | -- | -- | -- | 384 (S) |
| 2 | 220 (LM) | 226 (LM) | 220 (S) | 10 | 400 (Lm) | 392 (Lm) | -- |
| -- | -- | -- | 226 (Lm) | -- | -- | -- | 410 (LM) [A] |
| 3 | 230 (LM) | 238 (LM) | 240 (LM) | 11 | 428 (S) | 415 (S) | -- |
| 4 | 250 (Lm) | 249 (LM) | 259 (LM) | -- | -- | -- | 453 (Lm) |
| 5 | 277 (S) | 263 (S) 275 (S) | 270 (LM) | 12 | 456 (LM) | 445 (LM) | -- |
| 6 | 298 (LM) | 281 (LM) | 292 (S) | -- | -- | -- | 485 (LM) |
| -- | -- | 292 (Lm) | 305 (Lm) | 13 | 500 (S) | 511 (LM) | -- |
| 7 | 305 (LM) | 317 (LM) | 319 (LM) | -- | -- | -- | 550 (S) |
| 8 | 322 (S) | 330 (S) | 325 (S) | 14 | 612 (S) | 575 (S) | 617 (LM) |
| 9 | 340 (S) | 340 (S) | 340 (S) | 15 | 700 (S) | 690 (LM) [B] | 700 (S) |
| -- | -- | 367 (LM) [A] | 355 (Lm) | -- | -- | -- | 800 (LM) [B] |
| Molecule | Adhesion Energy (eV) |
|---|---|
| Model 1-a | −5.37 |
| Model 1-b | −6.73 |
| Model 1-c | −7.85 |
| Model 1-d | −10.99 |
| Molecule | Adhesion Energy (eV)—Single Molecule | Stacked Molecules |
|---|---|---|
| Model 1-a | −8.76 | −8.23 |
| Model 1-b | −8.93 | −7.95 |
| Model 1-c | −9.89 | −9.02 |
| Model 1-d | −11.02 | −10.90 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pinna, E.; Melis, C.; Antidormi, A.; Cardia, R.; Sechi, E.; Cappellini, G.; D’Ischia, M.; Colombo, L.; Mula, G. Deciphering Molecular Mechanisms of Interface Buildup and Stability in Porous Si/Eumelanin Hybrids. Int. J. Mol. Sci. 2017, 18, 1567. https://doi.org/10.3390/ijms18071567
Pinna E, Melis C, Antidormi A, Cardia R, Sechi E, Cappellini G, D’Ischia M, Colombo L, Mula G. Deciphering Molecular Mechanisms of Interface Buildup and Stability in Porous Si/Eumelanin Hybrids. International Journal of Molecular Sciences. 2017; 18(7):1567. https://doi.org/10.3390/ijms18071567
Chicago/Turabian StylePinna, Elisa, Claudio Melis, Aleandro Antidormi, Roberto Cardia, Elisa Sechi, Giancarlo Cappellini, Marco D’Ischia, Luciano Colombo, and Guido Mula. 2017. "Deciphering Molecular Mechanisms of Interface Buildup and Stability in Porous Si/Eumelanin Hybrids" International Journal of Molecular Sciences 18, no. 7: 1567. https://doi.org/10.3390/ijms18071567
APA StylePinna, E., Melis, C., Antidormi, A., Cardia, R., Sechi, E., Cappellini, G., D’Ischia, M., Colombo, L., & Mula, G. (2017). Deciphering Molecular Mechanisms of Interface Buildup and Stability in Porous Si/Eumelanin Hybrids. International Journal of Molecular Sciences, 18(7), 1567. https://doi.org/10.3390/ijms18071567