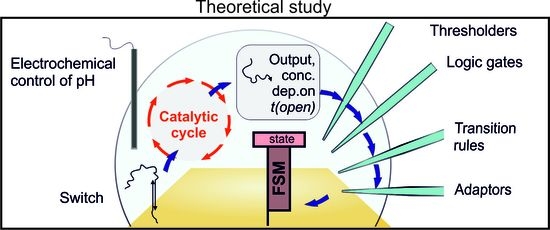
Towards a Bioelectronic Computer: A Theoretical Study of a Multi-Layer Biomolecular Computing System That Can Process Electronic Inputs
Abstract
:1. Introduction
2. Results
2.1. A Catalytic Cycle with an Electrochemically Controlled pH-Sensitive Nanoswitch as the Catalyst
2.2. Using a Thresholding Mechanism to Assess the Concentration of the Output from the Catalytic Cycle
2.3. Activation and Deactivation of Dumb-Bell Logic Gates
2.4. Operating a Finite State Machine Using the Dumb-Bell Logic Gates as Input
2.5. Readout Schemes
3. Discussion
4. Materials and Methods
4.1. Calculating the Effect of a Voltage Pulse on the pH-Sensitive Nanoswitch
4.2. Simulating the Behaviour of a Zhang Catalytic Cycle Where the Catalyst Is a pH-Sensitive Nanoswitch
4.3. Modelling the Thresholders
= xTOT − Σm(Lm,TOT − Am,TOT + [Am] + thm,TOT − [thm])
4.4. Simulating the Dynamics of the Dumb-Bell Logic Gates
kg3a,g3b = 2.5 × 106 M−1·s−1
kg4a = 2.5 × 105 M−1·s−1
4.5. Simulating the Behaviour of the Finite State Machine
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Seeman, N.C. Nucleic acid junctions and lattices. J. Theor. Biol. 1982, 99, 237–247. [Google Scholar] [CrossRef]
- Rothemund, P.W.K. Folding DNA to create nanoscale shapes and patterns. Nature 2006, 440, 297–302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shen, B.; Link, V.; Tapio, K.; Pikker, S.; Lemma, T.; Gopinath, A.; Gothelf, K.V.; Kostiainen, M.A.; Toppari, J.J. Plasmonic structures through DNA-assisted lithography. Sci. Adv. 2018, 4, eaap8978. [Google Scholar] [CrossRef] [PubMed]
- Ketterer, P.; Ananth, A.N.; Laman Trip, D.S.; Mishra, A.; Bertosin, A.; Ganji, M.; van der Torre, K.; Onck, P.; Dietz, H.; Dekker, C. DNA origami scaffold for studying intrinsically disordered proteins of the nuclear pore complex. Nat. Commun. 2018, 9, 902. [Google Scholar] [CrossRef] [PubMed]
- Funke, J.J.; Dietz, H. Placing molecules with Bohr radius resolution using DNA origami. Nat. Nanotechnol. 2016, 1, 47–52. [Google Scholar] [CrossRef] [PubMed]
- Komiyama, M.; Yoshimoto, K.; Sisido, M.; Ariga, K. Chemistry Can Make Strict and Fuzzy Controls for Bio-Systems: DNA Nanoarchitectonics and Cell-Macromolecular Nanoarchitectonics. Bull. Chem. Soc. Jpn. 2017, 90, 967–1004. [Google Scholar] [CrossRef] [Green Version]
- Sherman, W.B.; Seeman, N.C. A precisely controlled DNA biped walking device. Nano Lett. 2004, 4, 1203–1207. [Google Scholar] [CrossRef]
- Shin, J.S.; Pierce, N.A. A synthetic DNA walker for molecular transport. J. Am. Chem. Soc. 2004, 126, 10834–10835. [Google Scholar] [CrossRef]
- Qu, X.; Zhu, D.; Yao, G.; Su, S.; Chao, J.; Liu, H.; Zuo, X.; Wang, L.; Shi, J.; Wang, L.; et al. An Exonuclease III-Powered, On-Particle Stochastic DNA Walker. Angew. Chem. Int. Ed. 2017, 56, 1855–1858. [Google Scholar] [CrossRef] [PubMed]
- Pandian, G.N.; Sugiyama, H. Nature-Inspired Design of Smart Biomaterials Using the Chemical Biology of Nucleic Acids. Bull. Chem. Soc. Jpn. 2016, 89, 843–868. [Google Scholar] [CrossRef] [Green Version]
- Kahn, J.S.; Hu, Y.; Willner, I. Stimuli-Responsive DNA-Based Hydrogels: From Basic Principles to Applications. Acc. Chem. Res. 2017, 50, 680–690. [Google Scholar] [CrossRef] [PubMed]
- Praetorius, F.; Kick, B.; Behler, K.L.; Honemann, M.N.; Weuster-Botz, D.; Dietz, H. Biotechnological mass production of DNA origami. Nature 2017, 552, 84–87. [Google Scholar] [CrossRef] [PubMed]
- Burns, J.R.; Lamarre, B.; Pyne, A.L.B.; Noble, J.E.; Ryadnov, M. DNA Origami Inside-Out Viruses. ACS Synth. Biol. 2018, 7, 767–773. [Google Scholar] [CrossRef] [PubMed]
- Adleman, L.M. Molecular computation of solutions to combinatorial problems. Science 1994, 266, 1021–1024. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Seelig, G.; Soloveichik, D.; Zhang, D.Y.; Winfree, E. Enzyme-free nucleic acid logic circuits. Science 2006, 314, 1585–1588. [Google Scholar] [CrossRef] [PubMed]
- Frezza, B.M.; Cockroft, S.L.; Ghadiri, M.R. Modular multi-level circuits from immobilized DNA-based logic gates. J. Am. Chem. Soc. 2007, 129, 14875–14879. [Google Scholar] [CrossRef] [PubMed]
- Stojanovic, M.N.; Mitchell, T.E.; Stefanovich, D. Deoxyribozyme-based logic gates. J. Am. Chem. Soc. 2002, 124, 3115–3123. [Google Scholar] [CrossRef]
- Qian, L.; Winfree, E. A simple DNA gate motif for synthesizing large-scale circuits. J. R. Soc. Interface 2011, 8, 1281–1297. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qian, L.; Winfree, E. Scaling up digital circuit computation with DNA strand displacement cascades. Science 2011, 332, 1196–1201. [Google Scholar] [CrossRef] [PubMed]
- Qian, L.; Winfree, E.; Bruck, J. Neural network computation with DNA strand displacement cascades. Nature 2011, 475, 368–372. [Google Scholar] [CrossRef] [PubMed]
- Soloveichik, D.; Seelig, G.; Winfree, E. DNA as a universal substrate for chemical kinetics. Proc. Natl. Acad. Sci. USA 2010, 107, 5393–5398. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Benenson, Y.; Paz-Elizur, T.; Adar, R.; Keinan, E.; Livneh, Z.; Shapiro, E. Programmable and autonomous computing machine made of biomolecules. Nature 2001, 414, 430–434. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Costa Santini, C.; Bath, J.; Tyrrell, A.M.; Turberfield, A.J. A clocked finite state machine built from DNA. Chem. Commun. 2013, 49, 237–239. [Google Scholar] [CrossRef] [PubMed]
- Rothemund, P.W.K.; Papadakis, N.; Winfree, E. Algorithmic self-assembly of DNA Sierpinski triangles. PLoS Biol. 2013, 2, e424. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Currin, A.; Korovin, K.; Ababi, M.; Roper, K.; Kell, D.B.; Day, P.J.; King, R.D. Computing exponentially faster: Implementing a non-deterministic universal Turing machine using DNA. J. R. Soc. Interface 2017, 14, 20160990. [Google Scholar] [CrossRef] [PubMed]
- Dunn, K.E.; Trefzer, M.A.; Johnson, S.; Tyrrell, A.M. Assessing the potential of surface-immobilized molecular logic machines for integration with solid state technology. Biosystems 2016, 146, 3–9. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Liu, G.; Liu, H.; Li, D.; Fan, C.; Liu, D. An electrochemically actuated reversible DNA switch. Nano Lett. 2010, 10, 1393–1397. [Google Scholar] [CrossRef] [PubMed]
- Minero, G.A.S.; Wagler, P.F.; Oughli, A.A.; McCaskill, J.S. Electronic pH switching of DNA triplex reactions. RSC Adv. 2015, 5, 27313–27325. [Google Scholar] [CrossRef]
- Ranallo, S.; Amodio, A.; Idili, A.; Porchetta, A.; Ricci, F. Electronic control of DNA-based nanoswitches and nanodevices. Chem. Sci. 2016, 7, 66–71. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guz, N.; Fedotova, T.A.; Fratto, B.E.; Schlesinger, O.; Alfonta, L.; Kolpashchikov, D.M.; Katz, E. Bioelectronic interface connecting reversible logic gates based on enzyme and DNA reactions. ChemPhysChem 2016, 17, 2247–2455. [Google Scholar] [CrossRef] [PubMed]
- Fan, C.; Plaxco, K.W.; Heeger, A.J. Electrochemical interrogation of conformational changes as a reagentless method for the sequence-specific detection of DNA. Proc. Natl. Acad. Sci. USA 2003, 100, 9134–9137. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ge, L.; Wang, W.; Sun, X.; Hou, T.; Li, F. Versatile and programmable DNA logic gates on universal and label-free homogeneous electrochemical platform. Anal. Chem. 2016, 88, 9691–9698. [Google Scholar] [CrossRef] [PubMed]
- Frank-Kamenetskii, M.D.; Mirkin, S.M. Triplex DNA structures. Annu. Rev. Biochem. 1996, 392, 65–95. [Google Scholar] [CrossRef] [PubMed]
- Idili, A.; Vallée-Bélisle, A.; Ricci, F. Programmable pH-triggered DNA nanoswitches. J. Am. Chem. Soc. 2014, 136, 5836–5839. [Google Scholar] [CrossRef] [PubMed]
- Amodio, A.; Zhao, B.; Porchetta, A.; Idili, A.; Castronovo, M.; Fan, C.; Ricci, F. Rational design of pH-controlled DNA strand displacement. J. Am. Chem. Soc. 2014, 136, 16469–16472. [Google Scholar] [CrossRef] [PubMed]
- Idili, A.; Porchetta, A.; Amodio, A.; Vallée-Bélisle, A.; Ricci, F. Controlling hybridization chain reactions with pH. Nano Lett. 2015, 15, 5539–5544. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.Y.; Turberfield, A.J.; Yurke, B.; Winfree, E. Engineering entropy-driven reactions and networks catalyzed by DNA. Science 2007, 318, 1121–1125. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.Y.; Winfree, E. Control of DNA strand displacement kinetics using toehold exchange. J. Am. Chem. Soc. 2009, 131, 17303–17314. [Google Scholar] [CrossRef] [PubMed]
- Srinivas, N.; Ouldridge, T.E.; Šulc, P.; Schaeffer, J.M.; Yurke, B.; Louis, A.A.; Doye, J.P.K.; Winfree, E. On the biophysics and kinetics of toehold-mediated DNA strand displacement. Nucleic Acids Res. 2013, 41, 10641–10658. [Google Scholar] [CrossRef] [PubMed]
- Green, S.J.; Lubrich, D.; Turberfield, A.J. DNA Hairpins: Fuel for autonomous DNA devices. Biophys. J. 2006, 91, 2966–2975. [Google Scholar] [CrossRef] [PubMed]
- Machinek, R.R.F.; Ouldridge, T.E.; Haley, N.E.C.; Bath, J.; Turberfield, A.J. Programmable energy landscapes for kinetic control of DNA strand displacement. Nat. Commun. 2014, 5, 5324. [Google Scholar] [CrossRef] [PubMed]
- Morrison, L.E.; Stols, L.M. Sensitive fluorescence-based thermodynamic and kinetic measurement of DNA hybridization in solution. Biochemistry 1993, 32, 3095–3104. [Google Scholar] [CrossRef] [PubMed]
- Dunn, K.E.; Trefzer, M.A.; Johnson, S.; Tyrrell, A.M. Investigating the dynamics of surface-immobilized DNA nanomachines. Sci. Rep. 2016, 6, 29581. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kohne, D.E.; Levison, S.A.; Byers, M.J. Room temperature method for increasing the rate of DNA reassociation by many thousandfold: The Phenol Emulsion Reassociation Technique. Biochemistry 1977, 16, 5329–5341. [Google Scholar] [CrossRef] [PubMed]
- Dave, N.; Liu, J. Fast molecular beacon hybridization in organic solvents with increased target specificity. J. Phys. Chem. B 2010, 114, 15694–15699. [Google Scholar] [CrossRef] [PubMed]
- Bercovici, M.; Han, C.M.; Liao, J.C.; Santiago, J.G. Rapid hybridization of nucleic acids using isotachophoresis. Proc. Natl. Acad. Sci. USA 2012, 109, 11127–11132. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Han, C.M.; Katilus, E.; Santiago, J.G. Increasing hybridization rate and sensitivity of DNA microarrays using isotachophoresis. Lab Chip 2014, 14, 2958. [Google Scholar] [CrossRef] [PubMed]
- Schoen, I.; Krammer, H.; Braun, D. Hybridization kinetics is different inside cells. Proc. Natl. Acad. Sci. USA 2009, 106, 21649–21654. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mortensen, U.H.; Bendixen, C.; Sunjevaric, I.; Rothstein, R. DNA strand annealing is promoted by the yeast Rad52 protein. Proc. Natl. Acad. Sci. USA 1996, 93, 10729–10734. [Google Scholar] [CrossRef] [PubMed]
- Goodman, R.P. NANEV: A program employing evolutionary methods for the design of nucleic acid nanostructures. Biotechniques 2005, 38, 548–550. [Google Scholar] [CrossRef] [PubMed]
- Chatterjee, G.; Dalchau, N.; Muscat, R.A.; Phillips, A.; Seelig, G. A spatially localized architecture for fast and modular DNA computing. Nat. Nanotechnol. 2017, 12, 920–927. [Google Scholar] [CrossRef] [PubMed]





| Initial State | Initial State Vector | Signal | True Input | Input Vector | Final State | Final State Vector | |
|---|---|---|---|---|---|---|---|
| I | F | (1,0,0) | f | 1 | (1,0,0,0) | R | (0,0,1) |
| II | R | (0,0,1) | 2 | (0,1,0,0) | F | (1,0,0) | |
| III | F | (1,0,0) | 3 | (0,0,1,0) | L | (0,1,0) | |
| IV | L | (0,1,0) | l | 4 | (0,0,0,1) | F | (1,0,0) |
| sp | gq | Tpqr |
|---|---|---|
| (1,0,0) F | (1,0,0,0) | T11r = (0,0,1) |
| (0,1,0,0) | T12r = (1,0,0) | |
| (0,0,1,0) | T13r = (0,1,0) | |
| (0,0,0,1) | T14r = (1,0,0) | |
| (0,1,0) L | (1,0,0,0) | T21r = (0,0,0) |
| (0,1,0,0) | T22r = (0,0,0) | |
| (0,0,1,0) | T23r = (0,1,0) | |
| (0,0,0,1) | T24r = (1,0,0) | |
| (0,0,1) R | (1,0,0,0) | T31r = (0,0,1) |
| (0,1,0,0) | T32r = (1,0,0) | |
| (0,0,1,0) | T33r = (0,0,0) | |
| (0,0,0,1) | T44r = (0,0,0) |
| Initial State | [OB] (nM) | [A] (nM) | [B] (nM) | [C] (nM) | [D] (nM) | [G1act] (pM) | [G2act] (pM) | [G3act] (pM) | [G4act] (pM) | Final State | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| I | (1,0,0) | 1.5 | 0.122 | 0.004 | 0.001 | 0 | 96.084 | 2.841 | 0.931 | 0 | (0.0296, 0.0097, 0.9995) |
| II | (0.0296, 0.0097, 0.9995) | 2.8 | 0.443 | 0.194 | 0.015 | 0.002 | 8.520 | 86.072 | 6.229 | 0.571 | (0.9951, 0.0027, 0.0985) |
| III | (0.9951, 0.0027, 0.0985) | 3.9 | 0.715 | 0.465 | 0.215 | 0.024 | 0 | 1.044 | 69.702 | 3.560 | (0.0673, 0.9977, 0) |
| IV | (0.0673, 0.9977, 0) | 5.0 | 0.987 | 0.737 | 0.487 | 0.237 | 0 | 0 | 1.377 | 39.846 | (0.9994, 0.0345, 0) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dunn, K.E.; Trefzer, M.A.; Johnson, S.; Tyrrell, A.M. Towards a Bioelectronic Computer: A Theoretical Study of a Multi-Layer Biomolecular Computing System That Can Process Electronic Inputs. Int. J. Mol. Sci. 2018, 19, 2620. https://doi.org/10.3390/ijms19092620
Dunn KE, Trefzer MA, Johnson S, Tyrrell AM. Towards a Bioelectronic Computer: A Theoretical Study of a Multi-Layer Biomolecular Computing System That Can Process Electronic Inputs. International Journal of Molecular Sciences. 2018; 19(9):2620. https://doi.org/10.3390/ijms19092620
Chicago/Turabian StyleDunn, Katherine E., Martin A. Trefzer, Steven Johnson, and Andy M. Tyrrell. 2018. "Towards a Bioelectronic Computer: A Theoretical Study of a Multi-Layer Biomolecular Computing System That Can Process Electronic Inputs" International Journal of Molecular Sciences 19, no. 9: 2620. https://doi.org/10.3390/ijms19092620
APA StyleDunn, K. E., Trefzer, M. A., Johnson, S., & Tyrrell, A. M. (2018). Towards a Bioelectronic Computer: A Theoretical Study of a Multi-Layer Biomolecular Computing System That Can Process Electronic Inputs. International Journal of Molecular Sciences, 19(9), 2620. https://doi.org/10.3390/ijms19092620