Effect of Central Longitudinal Dipole Interactions on Chiral Liquid-Crystal Phases
Abstract
:1. Introduction
2. Results and Discussion
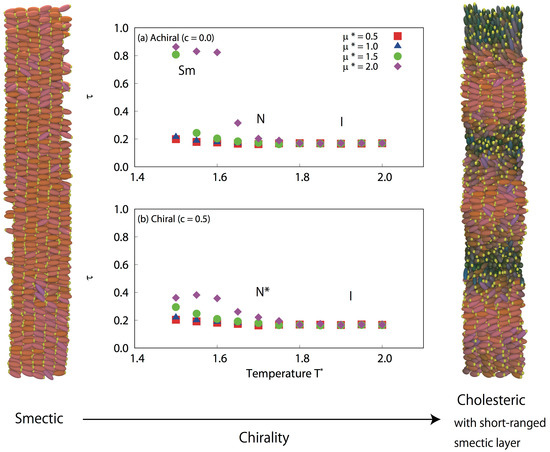
2.1. The Effect of Chirality on Non-Polar Liquid Crystals
2.2. Effect of Dipole Interactions
3. Conclusions
4. Methods
4.1. Fluid–Fluid Interactions
4.2. Fluid–Substrate Interactions
4.3. Orientational Order Parameter
4.4. Translational Order Parameter
4.5. Bond Order Parameter
4.6. Simulation Conditions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Effect of Confinement by Solid Substrates





Appendix B. Chiral Gay–Berne potential

References
- Kamien, R.D.; Lubensky, T. Twisted line liquids. J. Phys. I 1993, 3, 2131–2138. [Google Scholar] [CrossRef] [Green Version]
- Navailles, L.; Pansu, B.; Gorre-Talini, L.; Nguyen, H. Structural study of a commensurate TGB A phase and of a presumed chiral line liquid phase. Phys. Rev. Lett. 1998, 81, 4168–4171. [Google Scholar] [CrossRef]
- Chan, T.; Garland, C.W.; Nguyen, H. Calorimetric study of chiral liquid crystals with a twist-grain-boundary phase. Phys. Rev. E 1995, 52, 5000–5003. [Google Scholar] [CrossRef]
- Ybert, C.; Navailles, L.; Pansu, B.; Rieutord, F.; Nguyen, H.; Barois, P. Structural study of the liquid-crystal analog of the vortex liquid phase in type-II superconductors. Europhys. Lett. 2003, 63, 840–845. [Google Scholar] [CrossRef]
- Iannacchione, G.; Garland, C.; Mieczkowski, J.; Gorecka, E. Phase behavior in the reentrant-nematic region of chiral frustrated smectic liquid crystals. Phys. Rev. E 1998, 58, 595–601. [Google Scholar] [CrossRef]
- Anakkar, A.; Isaert, N.; Ismaili, M.; Buisine, J.M.; Nguyen, H. Experimental observation of multicritical behaviors in pressure-temperature diagrams of pure compounds with twist grain boundary phases. Phys. Rev. E 1999, 60, 620–627. [Google Scholar] [CrossRef]
- Ismaïli, M.; Anakkar, A.; Joly, G.; Isaert, N.; Nguyen, H. Multicritical behaviors and an induced twist grain boundary phase in a binary liquid crystalline mixture. Phys. Rev. E 2000, 61, 519–525. [Google Scholar] [CrossRef]
- Adorjan, A.; Stojadinovic, S.; Sukhomlinova, L.; Twieg, R.; Sprunt, S. Light scattering study of a twist grain boundary liquid crystal. Phys. Rev. Lett. 2003, 90, 035503. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, J.; Nishiyama, I.; Inoue, M.; Yokoyama, H. Optical isotropy and iridescence in a smectic ‘blue phase’. Nature 2005, 437, 525–528. [Google Scholar] [CrossRef] [PubMed]
- Cordoyiannis, G.; Jampani, V.S.R.; Kralj, S.; Dhara, S.; Tzitzios, V.; Basina, G.; Nounesis, G.; Kutnjak, Z.; Tripathi, C.S.P.; Losada-Pérez, P.; et al. Different modulated structures of topological defects stabilized by adaptive targeting nanoparticles. Soft Matter 2013, 9, 3956–3964. [Google Scholar] [CrossRef]
- Trček, M.; Cordoyiannis, G.; Tzitzios, V.; Kralj, S.; Nounesis, G.; Lelidis, I.; Kutnjak, Z. Nanoparticle-induced twist-grain boundary phase. Phys. Rev. E 2014, 90, 032501. [Google Scholar] [CrossRef] [PubMed]
- Sato, H.; Yamagishi, A. Application of Δ- and Λ-isomerism of Octahedral Metal Complexes for Inducing Chiral Nematic Phases. Int. J. Mol. Sci. 2009, 10, 4559–4574. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Wang, M.; Wang, L.; Yang, D.k.; Yu, H.; Yang, H. Polymeric infrared reflective thin films with ultra-broad bandwidth. Liq. Cryst. 2016, 43, 750–757. [Google Scholar] [CrossRef]
- Wang, L.; Dong, H.; Li, Y.; Xue, C.; Sun, L.D.; Yan, C.H.; Li, Q. Reversible near-infrared light directed reflection in a self-organized helical superstructure loaded with upconversion nanoparticles. J. Am. Chem. Soc. 2014, 136, 4480–4483. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Dong, H.; Li, Y.; Liu, R.; Wang, Y.F.; Bisoyi, H.K.; Sun, L.D.; Yan, C.H.; Li, Q. Luminescence-driven reversible handedness inversion of self-organized helical superstructures enabled by a novel near-infrared light nanotransducer. Adv. Mater. 2015, 27, 2065–2069. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Chen, D.; Gutierrez-Cuevas, K.G.; Bisoyi, H.K.; Fan, J.; Zola, R.S.; Li, G.; Urbas, A.M.; Bunning, T.J.; Weitz, D.A.; et al. Optically reconfigurable chiral microspheres of self-organized helical superstructures with handedness inversion. Mater. Horiz. 2017, 4, 1190–1195. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Bisoyi, H.K.; Zheng, Z.; Gutierrez-Cuevas, K.G.; Singh, G.; Kumar, S.; Bunning, T.J.; Li, Q. Stimuli-directed self-organized chiral superstructures for adaptive windows enabled by mesogen-functionalized graphene. Mater. Today 2017, 20, 230–237. [Google Scholar] [CrossRef]
- Wang, L.; Li, Q. Photochromism into nanosystems: Towards lighting up the future nanoworld. Chem. Soc. Rev. 2018, 47, 1044–1097. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Li, Q. Stimuli-Directing Self-Organized 3D Liquid-Crystalline Nanostructures: From Materials Design to Photonic Applications. Adv. Func. Mater. 2016, 26, 10–28. [Google Scholar] [CrossRef]
- Dussi, S.; Dijkstra, M. Entropy-driven formation of chiral nematic phases by computer simulations. Nat. Commun. 2016, 7, 11175. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barry, E.; Hensel, Z.; Dogic, Z.; Shribak, M.; Oldenbourg, R. Entropy-Driven Formation of a Chiral Liquid- Crystalline Phase of Helical Filaments. Phys. Rev. Lett. 2006, 96, 018305. [Google Scholar] [CrossRef] [PubMed]
- Gay, J.G.; Berne, B.J. Modification of the overlap potential to mimic a linear site-site potential. J. Chem. Phys. 1981, 74, 3316–3319. [Google Scholar] [CrossRef]
- Wilson, M.R. Molecular dynamics simulations of flexible liquid crystal molecules using a Gay–Berne/Lennard-Jones model. J. Chem. Phys. 1997, 107, 8654–8663. [Google Scholar] [CrossRef]
- McBride, C.; Wilson, M.R. Molecular dynamics simulations of a flexible liquid crystal. Mol. Phys. 1999, 97, 511–522. [Google Scholar] [CrossRef]
- Fukunaga, H.; Takimoto, J.; Doi, M. Molecular dynamics simulation study on the phase behavior of the Gay–Berne model with a terminal dipole and a flexible tail. J. Chem. Phys. 2004, 120, 7792–7800. [Google Scholar] [CrossRef] [PubMed]
- Prampolini, G. Parametrization and validation of coarse grained force-fields derived from ab initio calculations. J. Chem. Theory Comput. 2006, 2, 556–567. [Google Scholar] [CrossRef] [PubMed]
- Tagashira, K.; Takahashi, K.Z.; Fukuda, J.I.; Aoyagi, T. Development of Coarse-Grained Liquid-Crystal Polymer Model with Efficient Electrostatic Interaction: Toward Molecular Dynamics Simulations of Electroactive Materials. Materials 2018, 11, 83. [Google Scholar] [CrossRef] [PubMed]
- Memmer, R.; Kuball, H.G.; Schönhofer, A. Computer simulation of chiral liquid crystal phases. I. The polymorphism of the chiral Gay–Berne fluid. Liq. Cryst. 1993, 15, 345–360. [Google Scholar] [CrossRef]
- Memmer, R.; Kuball, H.G.; Schönhofer, A. Computer simulation of chiral liquid crystal phases. IV. Intermolecular chirality transfer to rotamers in a cholesteric phase. Liq. Cryst. 1995, 19, 749–753. [Google Scholar] [CrossRef]
- Memmer, R. Computer simulation of chiral liquid crystal phases III. A cholesteric phase formed by chiral Gay–Berne atropisomers. Mol. Phys. 1996, 89, 1633–1649. [Google Scholar]
- Memmer, R. Computer simulation of chiral liquid crystal phases—VII. The Chiral Gay–Berne Discogen. Ber. Bunsen-Ges. Phys. Chem. 1998, 102, 1002–1010. [Google Scholar] [CrossRef]
- Memmer, R. Determination of equilibrium pitch of cholesteric phases by isobaric-isothermal Monte Carlo simulation. J. Chem. Phys. 2001, 114, 8210–8222. [Google Scholar] [CrossRef]
- Memmer, R. Liquid crystal phases of achiral banana-shaped molecules: A computer simulation study. Liq. Cryst. 2002, 29, 483–496. [Google Scholar] [CrossRef]
- Memmer, R.; Fliegans, O. Monte Carlo simulation of twisted nematic and supertwisted nematic liquid crystal cells. Phys. Chem. Chem. Phys. 2003, 5, 558–566. [Google Scholar] [CrossRef]
- Allen, M.P.; Warren, M.A.; Wilson, M.R. Molecular-dynamics simulation of the smectic-A* twist grain-boundary phase. Phys. Rev. E 1998, 57, 5585–5596. [Google Scholar] [CrossRef]
- Berardi, R.; Kuball, H.G.; Memmer, R.; Zannoni, C. Chiral induction in nematics a computer simulation study. J. Chem. Soc. Faraday Trans. 1998, 94, 1229–1234. [Google Scholar] [CrossRef]
- Sarman, S.; Laaksonen, A. Thermomechanical coupling, heat conduction and director rotation in cholesteric liquid crystals studied by molecular dynamics simulation. Phys. Chem. Chem. Phys. 2013, 15, 3442–3453. [Google Scholar] [CrossRef] [PubMed]
- Melle, M.; Theile, M.; Hall, C.K.; Schoen, M. Nanoconfinement-induced structures in chiral liquid crystals. Int. J. Mol. Sci. 2013, 14, 17584–17607. [Google Scholar] [CrossRef] [PubMed]
- Schlotthauer, S.; Skutnik, R.A.; Stieger, T.; Schoen, M. Defect topologies in chiral liquid crystals confined to mesoscopic channels. J. Chem. Phys. 2015, 142, 194704. [Google Scholar] [CrossRef] [PubMed]
- Yan, F.; Hixson, C.A.; Earl, D.J. Computer simulations of linear rigid particles that form chiral superstructures and tilted smectic phases. Soft Matter 2009, 5, 4477–4483. [Google Scholar] [CrossRef]
- Gil-Villegas, A.; McGrother, S.C.; Jackson, G. Chain and ring structures in smectic phases of molecules with transverse dipoles. Chem. Phys. Lett. 1997, 269, 441–447. [Google Scholar] [CrossRef]
- Gil-Villegas, A.; McGrother, S.C.; Jackson, G. Reaction-field and Ewald summation methods in Monte Carlo simulations of dipolar liquid crystals. Mol. Phys. 1997, 92, 723–734. [Google Scholar] [CrossRef]
- Gil-Villegas, A.; Jackson, G.; McGrother, S.C. Computer simulation of dipolar liquid crystals. J. Mol. Liq. 1998, 76, 171–181. [Google Scholar] [CrossRef]
- McGrother, S.C.; Williamson, D.C.; Jackson, G. A re-examination of the phase diagram of hard spherocylinders. J. Chem. Phys. 1996, 104, 6755–6771. [Google Scholar] [CrossRef]
- Satoh, K.; Mita, S.; Kondo, S. Monte Carlo simulations using the dipolar Gay–Berne model: Effect of terminal dipole moment on mesophase formation. Chem. Phys. Lett. 1996, 255, 99–104. [Google Scholar] [CrossRef]
- Gwóźdź, E.; Bródka, A.; Pasterny, K. Molecular dynamics simulation study of a liquid crystal model: Gay–Berne particles with transverse dipole moments. Chem. Phys. Lett. 1997, 267, 557–562. [Google Scholar] [CrossRef]
- Satoh, K.; Mita, S.; Kondo, S. Monte Carlo simulations on mesophase formation using dipolar Gay–Berne model. Liq. Cryst. 1996, 20, 757–763. [Google Scholar] [CrossRef]
- Houssa, M.; Rull, L.F.; McGrother, S.C. Effect of dipolar interactions on the phase behavior of the Gay–Berne liquid crystal model. J. Chem. Phys. 1998, 109, 9529–9542. [Google Scholar] [CrossRef]
- De Gennes, P. Interactions between solid surfaces in a presmectic fluid. Langmuir 1990, 6, 1448–1450. [Google Scholar] [CrossRef]
- Dogic, Z.; Fraden, S. Cholesteric Phase in Virus Suspensions. Langmuir 2000, 16, 7820–7824. [Google Scholar] [CrossRef] [Green Version]
- Kralj, S.; Cordoyiannis, G.; Zidanšek, A.; Lahajnar, G.; Amenitsch, H.; Žumer, S.; Kutnjak, Z. Presmectic wetting and supercritical-like phase behavior of octylcyanobiphenyl liquid crystal confined to controlled-pore glass matrices. J. Chem. Phys. 2007, 127, 154905. [Google Scholar] [CrossRef] [PubMed]
- van der Schoot, P. Self-assembly of globular particles in a nematic dispersion of colloidal rods. J. Chem. Phys. 2002, 117, 3537–3540. [Google Scholar] [CrossRef]
- Savenko, S.V.; Dijkstra, M. Accuracy of measuring the nematic order from intensity scatter: A simulation study. Phys. Rev. E 2004, 70, 011705. [Google Scholar] [CrossRef] [PubMed]
- Houssa, M.; Rull, L.F.; Romero-Enrique, J.M. Bilayered smectic phase polymorphism in the dipolar Gay–Berne liquid crystal model. J. Chem. Phys. 2009, 130, 154504. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bates, M.; Luckhurst, G. Computer simulation studies of anisotropic systems. XXX. The phase behavior and structure of a Gay–Berne mesogen. J. Chem. Phys. 1999, 110, 7087–7108. [Google Scholar] [CrossRef]
- de Miguel, E.; Martin del Rio, E.; Blas, F.J. Stability of smectic phases in the Gay–Berne model. J. Chem. Phys. 2004, 121, 11183–11194. [Google Scholar] [CrossRef] [PubMed]
- Saielli, G.; Margola, T.; Satoh, K. Tuning Coulombic interactions to stabilize nematic and smectic ionic liquid crystal phases in mixtures of charged soft ellipsoids and spheres. Soft Matter 2017, 13, 5204–5213. [Google Scholar] [CrossRef] [PubMed]
- Berg, B.A.; Neuhaus, T. Multicanonical ensemble: A new approach to simulate first-order phase transitions. Phys. Rev. Lett. 1992, 68, 9. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Keyes, T.; Straub, J.E. Generalized replica exchange method. J. Chem. Phys. 2010, 132, 224107. [Google Scholar] [CrossRef] [PubMed]
- Mazza, M.G.; Schoen, M. Structure and dynamics of reentrant nematics: Any open questions after almost 40 years? Int. J. Mol. Sci. 2011, 12, 5352–5372. [Google Scholar] [CrossRef] [PubMed]
- Stieger, T.; Mazza, M.G.; Schoen, M. Diffusivity Maximum in a Reentrant Nematic Phase. Int. J. Mol. Sci. 2012, 13, 7854–7871. [Google Scholar] [CrossRef] [PubMed] [Green Version]












© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nozawa, T.; Brumby, P.E.; Yasuoka, K. Effect of Central Longitudinal Dipole Interactions on Chiral Liquid-Crystal Phases. Int. J. Mol. Sci. 2018, 19, 2715. https://doi.org/10.3390/ijms19092715
Nozawa T, Brumby PE, Yasuoka K. Effect of Central Longitudinal Dipole Interactions on Chiral Liquid-Crystal Phases. International Journal of Molecular Sciences. 2018; 19(9):2715. https://doi.org/10.3390/ijms19092715
Chicago/Turabian StyleNozawa, Takuma, Paul E. Brumby, and Kenji Yasuoka. 2018. "Effect of Central Longitudinal Dipole Interactions on Chiral Liquid-Crystal Phases" International Journal of Molecular Sciences 19, no. 9: 2715. https://doi.org/10.3390/ijms19092715
APA StyleNozawa, T., Brumby, P. E., & Yasuoka, K. (2018). Effect of Central Longitudinal Dipole Interactions on Chiral Liquid-Crystal Phases. International Journal of Molecular Sciences, 19(9), 2715. https://doi.org/10.3390/ijms19092715