Different Dynamics in 6aJL2 Proteins Associated with AL Amyloidosis, a Conformational Disease
Abstract
:1. Introduction
2. Results
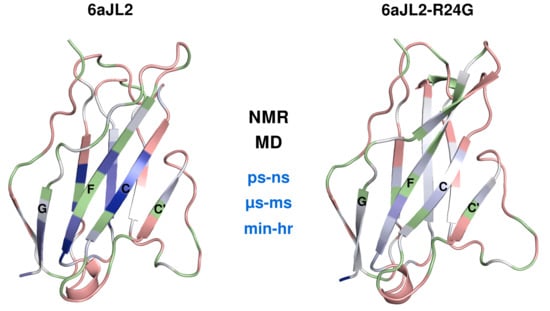
2.1. Fast Timescale Backbone Dynamics
2.2. Molecular Dynamics
2.3. Medium Timescale Backbone Dynamics
2.4. Hydrogen Deuterium Exchange
3. Discussion
4. Materials and Methods
4.1. Protein Expression and Purification
4.2. Dynamic Light Scattering
4.3. Nuclear Magnetic Resonance
4.4. Molecular Dynamics
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AL | Light-chain amyloidosis |
| NMR | Nuclear Magnetic Resonance |
| LC | light chain |
| MD | Molecular dynamics simulations |
References
- Vaxman, I.; Gertz, M. Recent Advances in the Diagnosis, Risk Stratification, and Management of Systemic Light-Chain Amyloidosis. Acta Haematol. 2019, 55905, 93–106. [Google Scholar] [CrossRef] [PubMed]
- Merlini, G.; Comenzo, R.L.; Seldin, D.C.; Wechalekar, A.; Gertz, M.A. Immunoglobulin light chain amyloidosis. Expert Rev. Hematol. 2014, 7, 143–156. [Google Scholar] [CrossRef] [PubMed]
- Blancas-Mejia, L.M.; Misra, P.; Dick, C.J.; Cooper, S.A.; Redhage, K.R.; Bergman, M.R.; Jordan, T.L.; Maara, K.; Ramirez-Alvarado, M. Immunoglobulin light chain amyloid aggregation. Chem. Commun. 2018, 54, 10664–10674. [Google Scholar] [CrossRef]
- Weiss, B.M.; Wong, S.W.; Comenzo, R.L. Blood Spotlight Beyond the plasma cell: Emerging therapies for immunoglobulin light chain amyloidosis. Blood 2016, 127, 2275–2281. [Google Scholar] [CrossRef] [PubMed]
- Comenzo, R.L.; Zhang, Y.; Martinez, C.; Osman, K.; Herrera, G.A. The tropism of organ involvement in primary systemic amyloidosis: Contributions of Ig VLgerm line gene use and clonal plasma cell burden. Blood 2001, 98, 714–720. [Google Scholar] [CrossRef] [PubMed]
- Abraham, R.S.; Geyer, S.M.; Ramirez-Alvarado, M.; Price-Troska, T.L.; Gertz, M.A.; Fonseca, R. Analysis of somatic hypermutation and antigenic selection in the clonal B cell in immunoglobulin light chain amyloidosis (AL). J. Clin. Immunol. 2004, 24, 340–353. [Google Scholar] [CrossRef] [PubMed]
- Enqvist, S.; Sletten, K.; Stevens, F.J.; Hellman, U.; Westermark, P. Germ line origin and somatic mutations determine the target tissues in systemic AL-amyloidosis. PLoS ONE 2007, 2, e981. [Google Scholar] [CrossRef] [PubMed]
- Villalba, M.I.; Canul-Tec, J.C.; Luna-Martínez, O.D.; Sánchez-Alcalá, R.; Olamendi-Portugal, T.; Rudiño-Piñera, E.; Rojas, S.; Sánchez-López, R.; Fernández-Velasco, D.A.; Becerril, B. Site-directed mutagenesis reveals regions implicated in the stability and fiber formation of human λ3r light chains. J. Biol. Chem. 2015, 290, 2577–2592. [Google Scholar] [CrossRef]
- Al-Lazikani, B.; Lesk, A.M.; Chothia, C. Standard conformations for the canonical structures of immunoglobulins. J. Mol. Biol. 1997, 273, 927–948. [Google Scholar] [CrossRef] [PubMed]
- González-Andrade, M.; Becerril-Luján, B.; Sánchez-Lõpez, R.; Ceceña-Álvarez, H.; Pérez-Carreõn, J.I.; Ortiz, E.; Fernández-Velasco, D.A.; Del Pozo-Yauner, L. Mutational and genetic determinants of λ6 light chain amyloidogenesis. FEBS J. 2013, 280, 6173–6183. [Google Scholar] [CrossRef] [PubMed]
- Del Pozo Yauner, L.; Ortiz, E.; Sánchez, R.; Sánchez-López, R.; Güereca, L.; Murphy, C.L.; Allen, A.; Wall, J.S.; Fernández-Velasco, D.A.; Solomon, A.; et al. Influence of the germline sequence on the thermodynamic stability and fibrillogenicity of human lambda 6 light chains. Proteins Struct. Funct. Genet. 2008, 72, 684–692. [Google Scholar] [CrossRef]
- Sánchez, S.A.G.; Álvarez, F.J.R.; Zavala-Padilla, G.; Mejia-Cristobal, L.M.; Cruz-Rangel, A.; Costas, M.; Velasco, D.A.F.; Melendez-Zajgla, J.; del Pozo-Yauner, L. Stability and aggregation propensity do not fully account for the association of various germline variable domain gene segments with light chain amyloidosis. Biol. Chem. 2017, 398, 477–489. [Google Scholar] [CrossRef] [PubMed]
- Maya-Martinez, R.; Gil-Rodriguez, P.; Amero, C. Solution structure of 6aJL2 and 6aJL2-R24G amyloidogenics light chain proteins. Biochem. Biophys. Res. Commun. 2015, 456, 695–699. [Google Scholar] [CrossRef]
- Hernández-Santoyo, A.; del Pozo Yauner, L.; Fuentes-Silva, D.; Ortiz, E.; Rudiño-Piñera, E.; Sánchez-López, R.; Horjales, E.; Becerril, B.; Rodríguez-Romero, A. A single mutation at the sheet switch region results in conformational changes favoring λ6 light-chain fibrillogenesis. J. Mol. Biol. 2010, 396, 280–292. [Google Scholar] [CrossRef] [PubMed]
- Luna-Martínez, O.D.; Hernández-Santoyo, A.; Villalba-Velázquez, M.I.; Sánchez-Alcalá, R.; Fernández-Velasco, D.A.; Becerril, B. Stabilizing an amyloidogenic λ6 light chain variable domain. FEBS J. 2017, 284, 3702–3717. [Google Scholar] [CrossRef] [PubMed]
- Pokkuluri, P.R.; Solomon, A.; Weiss, D.T.; Stevens, F.J. Tertiary structure of human γ6 light chains. Amyloid Int. J. Exp. Clin. Investig. 1999, 6, 165–171. [Google Scholar] [CrossRef]
- Del Pozo Yauner, L.; Ortiz, E.; Becerril, B. The CDR1 of the human λVI light chains adopts a new canonical structure. Proteins Struct. Funct. Genet. 2006, 62, 122–129. [Google Scholar] [CrossRef]
- Valdés-García, G.; Millan-Pacheco, C.; Pastor, N. Convergent mechanisms favor fast amyloid formation in two lambda 6a Ig light chain mutants. Biopolymers 2017, 107, e23027. [Google Scholar] [CrossRef]
- García De La Torre, J.; Huertas, M.L.; Carrasco, B. Calculation of hydrodynamic properties of globular proteins from their atomic-level structure. Biophys. J. 2000, 78, 719–730. [Google Scholar] [CrossRef]
- Velázquez-López, I.; Valdés-García, G.; Romero Romero, S.; Maya Martínez, R.; Leal-Cervantes, A.I.; Costas, M.; Sánchez-López, R.; Amero, C.; Pastor, N.; Fernández Velasco, D.A. Localized conformational changes trigger the pH-induced fibrillogenesis of an amyloidogenic λ light chain protein. Biochim. Biophys. Acta Gen. Subj. 2018, 1862, 1656–1666. [Google Scholar] [CrossRef]
- Baldwin, A.J.; Kay, L.E. NMR spectroscopy brings invisible protein states into focus. Nat. Chem. Biol. 2009, 5, 808–814. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, S.; Pondaven, S.P.; Jaroniec, C.P. Chain Variable Domain by Relaxation Dispersion Nuclear Magnetic and Amyloid Assembly. Biochemistry 2011, 5845–5857. [Google Scholar] [CrossRef] [PubMed]
- Stetefeld, J.; McKenna, S.A.; Patel, T.R. Dynamic light scattering: A practical guide and applications in biomedical sciences. Biophys. Rev. 2016, 8, 409–427. [Google Scholar] [CrossRef] [PubMed]
- Pastor, N.; Amero, C. Information flow and protein dynamics: The interplay between nuclear magnetic resonance spectroscopy and molecular dynamics simulations. Front. Plant Sci. 2015, 6, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Piszczek, G.; Schuck, P. SEDPHAT – a platform for global ITC analysis and global multi- method analysis of molecular interactions. Methods 2015, 76, 137–148. [Google Scholar] [CrossRef] [PubMed]
- Brautigam, C.A.; Zhao, H.; Vargas, C.; Keller, S.; Schuck, P. Integration and global analysis of isothermal titration calorimetry data for studying macromolecular interactions. Nat. Protoc. 2016, 11, 882–894. [Google Scholar] [CrossRef] [PubMed]
- Delaglio, F.; Grzesiek, S.; Vuister, G.W.; Zhu, G.; Pfeifer, J.; Bax, A. NMRPipe: A multidimensional spectral processing system based on UNIX pipes. J. Biomol. NMR 1995, 6, 277–293. [Google Scholar] [CrossRef] [PubMed]
- Keller, R. The Computer Aided Resonance Assignment Tutorial. Available online: http://cara.nmr-software.org/downloads/3-85600-112-3.pdf (accessed on 1 April 2019).
- D’Auvergne, E.J.; Gooley, P.R. Optimisation of NMR dynamic models I. Minimisation algorithms and their performance within the model-free and Brownian rotational diffusion spaces. J. Biomol. NMR 2008, 40, 107–119. [Google Scholar] [CrossRef]
- Lefèvre, J.-F.; Dayie, K.T.; Peng, J.W.; Wagner, G. Internal Mobility in the Partially Folded DNA Binding and Dimerization Domains of GAL4: NMR Analysis of the N−H Spectral Density Functions. Biochemistry 1996, 35, 2674–2686. [Google Scholar] [CrossRef]
- Brooks, B.R.; Bruccoleri, R.E.; Olafson, B.D.; States, D.J.; Swaminathan, S.; Karplus, M. CHARMM: A program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 1983, 4, 187–217. [Google Scholar] [CrossRef]
- Trbovic, N.; Kim, B.; Friesner, R.A.; Palmer, A.G. Structural analysis of protein dynamics by MD simulations and NMR spin-relaxation. Proteins Struct. Funct. Bioinform. 2009, 71, 684–694. [Google Scholar] [CrossRef] [PubMed]
- Zeiske, T.; Stafford, K.A.; Friesner, R.A.; Palmer, A.G. Starting-structure dependence of nanosecond timescale intersubstate transitions and reproducibility of MD-derived order parameters. Proteins Struct. Funct. Bioinform. 2013, 81, 499–509. [Google Scholar] [CrossRef] [PubMed]






| Mean Value | 6aJL2 | 6aJL2-R24G |
|---|---|---|
| R1 | 1.05 ± 0.08 (s−1) | 1.09 ± 0.06 (s−1) |
| R2 | 17.3 ± 3.3 (s−1) | 18.9 ± 4.2 (s−1) |
| HetNOE | 0.88 ± 0.04 | 0.88 ± 0.02 |
| 6aJL2 | 6aJL2-R24G | |
|---|---|---|
| kex | 1175 s−1 | 2008 s−1 |
| pB | 15% | 10% |
| Average Δω | 0.8 | 0.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maya-Martinez, R.; French-Pacheco, L.; Valdés-García, G.; Pastor, N.; Amero, C. Different Dynamics in 6aJL2 Proteins Associated with AL Amyloidosis, a Conformational Disease. Int. J. Mol. Sci. 2019, 20, 4078. https://doi.org/10.3390/ijms20174078
Maya-Martinez R, French-Pacheco L, Valdés-García G, Pastor N, Amero C. Different Dynamics in 6aJL2 Proteins Associated with AL Amyloidosis, a Conformational Disease. International Journal of Molecular Sciences. 2019; 20(17):4078. https://doi.org/10.3390/ijms20174078
Chicago/Turabian StyleMaya-Martinez, Roberto, Leidys French-Pacheco, Gilberto Valdés-García, Nina Pastor, and Carlos Amero. 2019. "Different Dynamics in 6aJL2 Proteins Associated with AL Amyloidosis, a Conformational Disease" International Journal of Molecular Sciences 20, no. 17: 4078. https://doi.org/10.3390/ijms20174078
APA StyleMaya-Martinez, R., French-Pacheco, L., Valdés-García, G., Pastor, N., & Amero, C. (2019). Different Dynamics in 6aJL2 Proteins Associated with AL Amyloidosis, a Conformational Disease. International Journal of Molecular Sciences, 20(17), 4078. https://doi.org/10.3390/ijms20174078