Magnetorheological Hybrid Elastomers Based on Silicone Rubber and Magnetorheological Suspensions with Graphene Nanoparticles: Effects of the Magnetic Field on the Relative Dielectric Permittivity and Electric Conductivity
Abstract
:1. Introduction
2. Results and Discussion
3. Materials and Methods
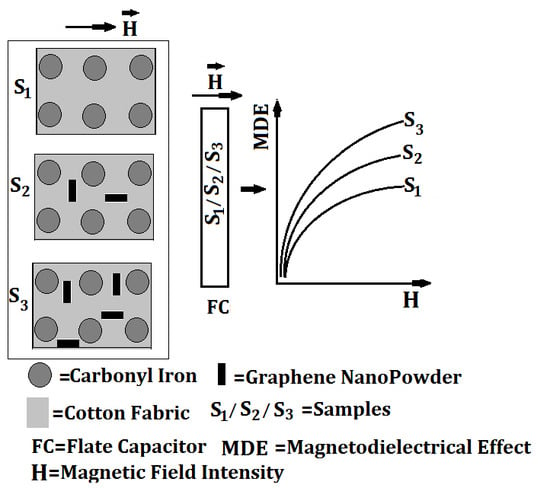
3.1. Materials
- Silicone Rubber (SR), from RTV-Silicone, a product having a white color, and density 2.30 g/cm3;
- Silicone Oil (SO), type C3518 from Sigma-Aldrich, with density 1.08 g/cm3;
- Carbonyl Iron (CI), type C3518, from Sigma-Aldrich, in the shape of spherical particles having diameters between 4.5 μm and 5.4 μm, a Fe content of at least 97% and a density of 7.86 g/cm3;
- Graphene NanoPowder (nGr), from Sky Spring Nanomaterials Inc., powder with Platelet Nanopowder of thickness between 6 nm and 8 nm, average diameter of 15 µM Graphene and density 2.28 g/cm3;
- gauze bandage (FT), from MKD Medicala with a granulation of 30 g/cm3;
- six textolite plates (TCu), copper-plated, from Sierra Modellsport.
3.2. The Manufacturing of the hMRE Membranes
3.3. Experimental Setup
- A—neodymium permanent magnet, type VMM12-N54, generating the magnetic field of intensity H;
- B—RLC bridge, type ET7-20, from MNIPI (Republic of Belarus);
- Gs—Gaussmeter, Type DX-102;
- FC—working capacitor, fixed on the Hall probe through a spacing device (not represented in Figure 1) that has a micrometre screw;
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MRE | Magnetorheological elastomer |
| hMRE | Hybrid magnetorheological elastomer |
| FC | Flat capacitor |
| SR | Silicone rubber |
| CI | Carbonyl iron |
| nGr | Graphene nanoparticles |
| FT | Gauze bandage |
| TCu | Copper-plated textolite plates |
References
- Rabbani, Y.; Ashtiani, M.; Hashemabadi, S.H. An experimental study on the effects of temperature and magnetic field strength on the magnetorheological fluid stability and MR effect. Soft Matter 2015, 11, 4453–4460. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Shin, K.Y.; Jang, J. Enhanced magnetorheological performance of highly uniform magnetic carbon nanoparticles. Nanoscale 2015, 7, 9646–9654. [Google Scholar] [CrossRef] [PubMed]
- Biller, A.M.; Stolbov, A.V.; Raikher, Y.L. Modeling of particle interactions in magnetorheological elastomers. J. Appl. Phys. 2014, 116, 114904. [Google Scholar] [CrossRef]
- Sedlacik, M.; Mrilik, M.; Babayan, V.; Pavlinek, V. Magnetorheological elastomers with efficient electromagnetic shielding. Compos. Struct. 2016, 135, 199–204. [Google Scholar] [CrossRef]
- Jung, H.S.; Kwon, S.H.; Choi, H.J.; Jung, J.H.; Kim, Y.G. Magnetic carbonyl iron/natural rubber composite elastomer and its magnetorheology. Compos. Struct. 2016, 136, 106–112. [Google Scholar] [CrossRef]
- Bunoiu, M.; Bica, I. Magnetorheological elastomer based on silicone rubber, carbonyl iron and Rochelle salt: Effects of alternating electric and static magnetic fields intensities. J. Ind. Eng. Chem. 2016, 37, 312–318. [Google Scholar] [CrossRef]
- Balasoiu, M.; Bica, I. Composite magnetorheological elastomers as dielectrics for plane capacitors: Effects of magnetic field intensity. Results Phys. 2016, 6, 192–202. [Google Scholar] [CrossRef]
- Balasoiu, M.; Lebedev, V.T.; Raikher, Y.L.; Bica, I.; Bunoiu, M. The implicit effect of texturizing field on the elastic properties of magnetic elastomers revealed by SANS. J. Magn. Magn. Mat. 2017, 431, 126–129. [Google Scholar] [CrossRef]
- Bica, I.; Anitas, E.M.; Bunoiu, M.; Vatzulik, B.; Juganaru, I. Hybrid magnetorheological elastomer: Influence of magnetic field and compression pressure on its electrical conductivity. J. Ind. Eng. Chem. 2014, 20, 3994–3999. [Google Scholar] [CrossRef]
- Bica, I. Magnetorheological elastomer-based quadrupolar element of electric circuits. Mat. Sci. Eng. B 2010, 166, 94–98. [Google Scholar] [CrossRef]
- Plachy, T.; Kratina, O.; Sedlacik, M. Porous magnetic materials based on EPDM rubberfilled with carbonyl iron particles. Compos. Struct. 2018, 192, 126–130. [Google Scholar] [CrossRef]
- Cvek, M.; Kracalik, M.; Sedlacik, M.; Mrlik, M.; Sedlarik, V. Reprocessing of injection-molded magnetorheological elastomers based on TPE matrix. Compos. Part B 2019, 172, 253–261. [Google Scholar] [CrossRef]
- Moucka, R.; Sedlacik, M.; Cvek, M. Dielectric properties of magnetorheological elastomers with different microstructure. Appl. Phys. Lett. 2018, 122901. [Google Scholar] [CrossRef]
- Ausanio, G.; Iannotti, V.; Ricciardi, E.; Lanotte, L.; Lanotte, L. Magneto-piezoresistance in Magnetorheological elastomers for magnetic induction gradient or position sensors. Sens. Actuators A 2014, 205, 235–239. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Li, J.; Li, W.; Du, H. A state-of-the-art review on magnetorheological elastomer devices. Smart Mater. Struct. 2014, 23, 123001. [Google Scholar] [CrossRef]
- Sun, S.; Yang, J.; Du, H.; Zhang, S.; Yan, T.; Nakano, M.; Li, W. Development of magnetorheological elastomers–based tuned mass damper for building protection from seismic events. J. Intell. Mater. Syst. Struct. 2018, 29, 1777–1789. [Google Scholar] [CrossRef]
- Pőssinger, T. Experimental Characterization, Modeling and Simulation of Magneto-Rheological Elastomers. Ph.D. Thesis, École Politechnique Université Paris-Saclay, Palaiseau, France, 2015. [Google Scholar]
- Böse, H.; Rabindranath, R.; Ehrlich, J. Soft magnetorheological elastomers as new actuators for valves. J. Intellig. Mater. Syst. Struct. 2012, 23, 989–994. [Google Scholar] [CrossRef]
- Huang, X.G.; Yan, Z.Y.; Liu, C.; Li, G.H.; Wang, J. Study on the resistance properties of magnetorheological elastomer. Mater. Res. Innov. 2015, 19, 924–928. [Google Scholar] [CrossRef]
- Wang, Y.; Xuan, S.; Dong, B.; Xu, F.; Gong, X. Stimuli dependent impedance of conductive magnetorheological elastomers. Smart Mater. Struct. 2016, 25, 025003. [Google Scholar] [CrossRef]
- Bica, I. Electroconductive Magnetorheological Suspensions: Production and Physical Processes. J. Ind. Eng. Chem. 2009, 15, 233–237. [Google Scholar] [CrossRef]
- Pavlenko, A.V.; Turik, A.V.; Reznichenko, L.A.; Shilkina, L.A.; Konstantinov, G.M. The magnetodielectric effect in Bi1/2La1/2MnO3 ceramics. Tech. Phys. Lett. 2013, 39, 78–80. [Google Scholar] [CrossRef]
- Fannin, P.C.; Scaife, B.K.; Charles, S.W. On the permittivity of magnetic colloids subject to a strong external magnetic field over the frequency range 50 kHz to 1 MHz. J. Magn. Magn. Mater. 1993, 122, 168–171. [Google Scholar] [CrossRef]
- Kubisz, L.; Skumiel, A.; Pankowski, E.; Jezierska, D.H. Magnetically induced anisotropy of electric permittivity in the PDMS ferromagnetic gel. J. Non-Cryst. Solids 2011, 357, 767–770. [Google Scholar] [CrossRef]
- Semisalova, A.S.; Perov, N.S.; Stepanov, G.V.; Kramarenko, E.Y.; Khokhlov, A.R. Strong magnetodielectric effects in magnetorheological elastomers. Soft Mater 2013, 9, 11318–11324. [Google Scholar] [CrossRef]
- Bica, I.; Anitas, E.M. Magnetodielectric effects in membranes based on magnetorheological bio-suspensions. Mater. Des. 2018, 155, 317–324. [Google Scholar] [CrossRef]
- Bica, I.; Anitas, E.M. Magnetic field intensity and graphene concentration effects on electrical and rheological properties of MREs-based membranes. Smart Mater. Struct. 2017, 26, 105038. [Google Scholar] [CrossRef] [Green Version]
- Petrin, A.B. Notes on the Microscopic Theory of Dielectric Polarization. High Temp. 2013, 51, 147–152. [Google Scholar] [CrossRef]
- Moliton, A. Applied Electromagnetism and Materials; Springer: New York, NY, USA, 2007. [Google Scholar]
- Li, Y.C.; Li, R.K.Y.; Tjong, S.C. Frequency and Temperature Dependences of Dielectric Dispersion and Electrical Properties of Polyvinylidene Fluoride/Expanded Graphite Composites. J. Nanomater. 2010, 2010, 261748. [Google Scholar] [CrossRef]







| Si | SR(g) | SO(g) | CI(g3) | nGr(g) |
|---|---|---|---|---|
| S1 | 6.90 | 1.08 | 7.86 | 0.00 |
| S2 | 5.75 | 1.08 | 7.86 | 1.13 |
| S3 | 4.60 | 1.08 | 7.86 | 2.26 |
| Mi | ||||
|---|---|---|---|---|
| M1 | 43.60 | 6.82 | 49.68 | 0.00 |
| M2 | 36.35 | 6.82 | 49.68 | 7.15 |
| M3 | 30.60 | 6.82 | 49.68 | 14.30 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bica, I.; Bunoiu, O.M. Magnetorheological Hybrid Elastomers Based on Silicone Rubber and Magnetorheological Suspensions with Graphene Nanoparticles: Effects of the Magnetic Field on the Relative Dielectric Permittivity and Electric Conductivity. Int. J. Mol. Sci. 2019, 20, 4201. https://doi.org/10.3390/ijms20174201
Bica I, Bunoiu OM. Magnetorheological Hybrid Elastomers Based on Silicone Rubber and Magnetorheological Suspensions with Graphene Nanoparticles: Effects of the Magnetic Field on the Relative Dielectric Permittivity and Electric Conductivity. International Journal of Molecular Sciences. 2019; 20(17):4201. https://doi.org/10.3390/ijms20174201
Chicago/Turabian StyleBica, Ioan, and Octavian Mădălin Bunoiu. 2019. "Magnetorheological Hybrid Elastomers Based on Silicone Rubber and Magnetorheological Suspensions with Graphene Nanoparticles: Effects of the Magnetic Field on the Relative Dielectric Permittivity and Electric Conductivity" International Journal of Molecular Sciences 20, no. 17: 4201. https://doi.org/10.3390/ijms20174201
APA StyleBica, I., & Bunoiu, O. M. (2019). Magnetorheological Hybrid Elastomers Based on Silicone Rubber and Magnetorheological Suspensions with Graphene Nanoparticles: Effects of the Magnetic Field on the Relative Dielectric Permittivity and Electric Conductivity. International Journal of Molecular Sciences, 20(17), 4201. https://doi.org/10.3390/ijms20174201