A Complete Cross Section Data Set for Electron Scattering by Pyridine: Modelling Electron Transport in the Energy Range 0–100 eV
Abstract
:1. Introduction
2. Results
2.1. Electron Scattering Measurements
2.1.1. Electron Energy Loss Spectra
2.1.2. Double Differential Ionization Cross Sections
2.2. Input Data for Modelling Electron Transport
2.2.1. Total Electron Scattering Cross Sections
2.2.2. Integral Elastic Scattering Cross Sections
2.2.3. Integral Inelastic Scattering Cross Sections
2.2.4. Angular Distribution Functions
2.2.5. Energy Loss Distribution Functions
3. Discussion
4. Materials and Methods
4.1. Experimental Systems
4.1.1. Linear Transmission-Beam Electrostatic Spectrometer
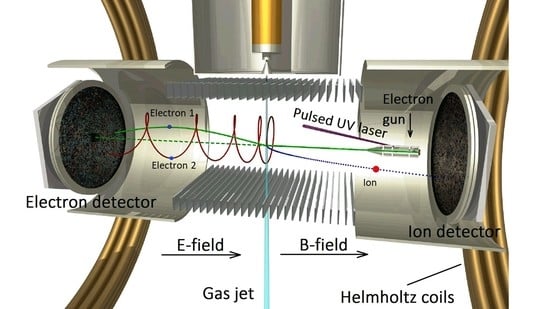
4.1.2. Double Electron-Ion Imaging Spectrometer (Reaction Microscope)
4.1.3. Magnetically Confined Electron Transmission Spectrometer
4.2. Theoretical Calculations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| IAM-SCAR | Independent atom model with screening corrected additivity rule and interference effects |
| SMC | Schwinger multichannel |
| DCS | Differential cross section |
| DDCS | Double differential cross section |
| MPIK | Max-Plank institute for nuclear physics |
| TCS | Total cross section |
| ICS | Integral cross section |
| IECS | Integral elastic cross section |
| SEP | Static-exchange-polarization |
| TICS | Total ionization cross section |
| DEA | Dissociative electron attachment |
| LEPTS | Low energy particle track simulation |
| EEL | Electron energy loss |
| SC | Scattering chamber |
| MCP | Micro channel plate |
| PC | Personal computer |
| RPA | Retarding potential analyzer |
| THF | Tetrahydrofuran |
References
- Sieradzka, A.; Blanco, F.; Fuss, M.C.; Masin, Z.; Gorfinkiel, J.D.; García, G. Electron scattering from pyridine. J. Phys. Chem. A 2014, 118, 6657–6663. [Google Scholar] [CrossRef] [PubMed]
- Traoré Dubuis, A.; Costa, F.; Ferreira da Silva, F.; Limão-Vieira, P.; Oller, J.C.; Blanco, F.; García, G. Total electron scattering cross section from pyridine molecules in the energy range 10–1000 eV. Chem. Phys. Lett. 2018, 699, 182–187. [Google Scholar] [CrossRef]
- Lozano, A.I.; Jiménez, J.; Blanco, F.; García, G. Total electron-scattering cross sections from pyridine molecules in the energy range 1–200 eV. Phys. Rev. A 2018, 98, 012709. [Google Scholar] [CrossRef] [Green Version]
- García Gómez-Tejedor, G.; Fuss, M.C. Radiation Damage in Biomolecular Systems; Springer: London, UK, 2012. [Google Scholar]
- Tanaka, H.; Brunger, M.J.; Campbell, L.; Kato, H.; Hoshino, M.; Rau, A.R.P. Scaled plane-wave Born cross sections for atoms and molecules. Rev. Mod. Phys 2016, 88, 025004. [Google Scholar] [CrossRef]
- Chen, W.; Chen, S.; Dong, Y.; Cloutier, P.; Zheng, Y.; Sanche, L. Absolute cross-sections for DNA strand breaks and crosslinks induced by low energy electrons. Phys. Chem. Chem. Phys. 2016, 18, 32762–32771. [Google Scholar] [CrossRef]
- Costa, F.; Álvarez, L.; Lozano, A.I.; Blanco, F.; Oller, J.C.; Muñoz, A.; Souza Barbosa, A.; Bettega, M.H.F.; Ferreira da Silva, F.; Limão-Vieira, P.; et al. Experimental and theoretical analysis for total electron scattering cross sections of benzene. J. Chem. Phys. 2019, 151, 084310. [Google Scholar] [CrossRef]
- Ullrich, J.; Moshammer, R.; Dorn, A.; Dörner, R.; Schmidt, L.P.H.; Schmidt-Böcking, H. Recoil-ion and electron momentum spectroscopy: Reaction-microscopes. Rep. Prog. Phys. 2003, 66, 1463–1545. [Google Scholar] [CrossRef]
- Dorn, A.; Kheifets, A.; Schröter, C.D.; Najjari, B.; Höhr, C.; Moshammer, R.; Ullrich, J. Double Ionization of Helium by Electron-Impact: Complete Pictures of the Four-Body Breakup Dynamics. Phys. Rev. Lett. 2001, 86, 3755–3758. [Google Scholar] [CrossRef] [Green Version]
- Wang, E.; Ren, X.; Baek, W.Y.; Rabus, H.; Pfeifer, T.; Dorn, A. Water acting as a catalyst for electron-driven molecular break-up of tetrahydrofuran. Nat. Commun. 2020, 11, 1–7. [Google Scholar] [CrossRef]
- Lozano, A.I.; Oller, J.C.; Krupa, K.; Ferreira da Silva, F.; Limão-Vieira, P.; Blanco, F.; Muñoz, A.; Colmenares, R.; García, G. Magnetically confined electron beam system for high resolution electron transmission-beam experiments. Rev. Sci. Instrum. 2018, 89, 063105. [Google Scholar] [CrossRef] [Green Version]
- Ren, X.; Bray, I.; Fursa, D.V.; Colgan, J.; Pindzola, M.S.; Pflüger, T.; Senftleben, A.; Xu, S.; Dorn, A.; Ullrich, J. Electron-impact ionization of helium: A comprehensive experiment benchmarks theory. Phys. Rev. A 2011, 83, 052711. [Google Scholar] [CrossRef] [Green Version]
- Blanco, F.; Muñoz, A.; Almeida, D.; Ferreira da Silva, F.; Limão-Vieira, P.; Fuss, M.C.; Sanz, A.G.; García, G. Modelling low energy electron and positron tracks in biologically relevant media. Eur. Phys. J. D 2013, 67, 199. [Google Scholar] [CrossRef]
- Szmytkowski, C.; Stefanowska, S.; Tańska, N.; Żywicka, B.; Ptasińska-Denga, E.; Możejko, P. Cross sections for electron collision with pyridine [C5H5N] molecule. Mol. Phys. 2019, 117, 395–403. [Google Scholar] [CrossRef]
- U.S. Department of Commerce. NIST Chemistry WebBook; U.S. Department of Commerce: Washington, DC, USA, 2017. Available online: https://webbook.nist.gov/chemistry/ (accessed on 27 August 2020).
- Fabrikant, I. Long-range effects in electron scattering by polar molecules. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 222005. [Google Scholar] [CrossRef]
- Álvarez, L.; Costa, F.; Lozano, A.I.; Oller, J.-C.; Muñoz, A.; Blanco, F.; Limão-Vieira, P.; White, R.D.; Brunger, M.J.; García, G. Electron scattering cross sections from nitrobenzene in the energy range 0.4–1000 eV: The role of dipole interactions in measurements and calculations. Phys. Chem. Chem. Phys. 2020, 22, 13505–13515. [Google Scholar] [CrossRef]
- Barbosa, A.S.; Pastega, D.F.; Bettega, M.H.F. Shape resonances in the elastic scattering of slow electrons by pyridine. Phys. Rev. A 2013, 88, 022705. [Google Scholar] [CrossRef]
- Mašín, Z.; Benda, J.; Gorfinkiel, J.D.; Harvey, A.G.; Tennyson, J. UKRmol+: A suite for modelling electronic processes in molecules interacting with electrons, positrons and photons using the R-matrix method. Comput. Phys. Commun. 2020, 249, 107092. [Google Scholar] [CrossRef] [Green Version]
- Jiao, C.Q.; Dejoseph, C.A., Jr.; Lee, R.; Garscadden, A. Kinetics of electron impact ionization and ion-molecule reactions of pyridine. Int. J. Mass Spectrom. 2006, 257, 34–40. [Google Scholar] [CrossRef]
- Bull, J.N.; Lee, J.W.L.; Vallance, C. Absolute electron total ionization cross-sections: Molecular analogues of DNA and RNA nucleobase and sugar constituents. Phys. Chem. Chem. Phys. 2014, 16, 10743–10752. [Google Scholar] [CrossRef]
- Chiari, L.; Zecca, A.; García, G.; Blanco, F.; Brunger, M.J. Low-energy positron and electron scattering from nitrogen dioxide. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 235202. [Google Scholar] [CrossRef]
- Lozano, A.I.; Oller, J.C.; Jones, D.B.; da Costa, R.F.; Varella, M.D.N.; Bettega, M.H.F.; Ferreira da Silva, F.; Limão-Vieira, P.; Lima, M.A.P.; White, R.D.; et al. Total electron scattering cross sections from para-benzoquinone in the energy range 1–200 eV. Phys. Chem. Chem. Phys. 2018, 20, 22368–22378. [Google Scholar] [CrossRef]
- Jones, D.B.; Blanco, F.; García, G.; da Costa, R.F.; Kossoski, F.; Varella, M.T.d.N.; Bettega, M.H.F.; Lima, M.A.P.; White, R.D.; Brunger, M.J. Elastic scattering and vibrational excitation for electron impact on para-benzoquinone. J. Chem. Phys. 2017, 147, 244304. [Google Scholar] [CrossRef]
- Maioli, L.S.; Bettega, M.H.F.; Blanco, F.; García, G.; Lange, E.; Limão-Vieira, P.; Ferreira da Silva, F. Theoretical and experimental cross sections for electron scattering from halothane. Eur. Phys. J. D 2019, 73, 181. [Google Scholar] [CrossRef]
- Gholami, N.; Hajivaliei, M.; Samei, M.E. Calculation of electron scattering cross sections for Anthracene, Pyridine and Warfarin molecules over energy range 10–30000 eV. Appl. Radiat. Isot. 2019, 150, 79–86. [Google Scholar] [CrossRef] [PubMed]
- Boudaïffa, B.; Cloutier, P.; Hunting, D.; Huels, M.A.; Sanche, L. Resonant formation of DNA strand breaks by low-energy (3 to 20 eV) electrons. Science 2000, 287, 1658–1660. [Google Scholar] [CrossRef] [PubMed]
- Lemelin, V.; Sanche, L. High-Resolution Electron Energy Loss Spectroscopy: Absolute Cross Section Measurements for Low Energy Electron Scattering from Biomolecules. In Radiation in Bioanalysis, Spectroscopic Techniques and Theoretical Methods; Pereira, A.S., Tavares, P., Limão-Vieira, P., Eds.; Springer Nature: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Blanco, F.; Muñoz, A.; Almeida, D.; Ferreira da Silva, F.; Limão-Vieira, P.; García, G. Clustering and condensation effects in the electron scattering cross sections from water molecules. Int. J. Mass Spectrom. 2014, 365–366, 287–294. [Google Scholar] [CrossRef]
- Ellis-Gibbings, L.; Bass, A.D.; Cloutier, P.; García, G.; Sanche, L. Electron stimulated desorption from condensed pyrimidine and pyridazine. Phys. Chem. Chem. Phys. 2017, 19, 13038–13048. [Google Scholar] [CrossRef]
- Traoré Dubuis, A.; Verkhovtsev, A.; Ellis-Gibbings, L.; Krupa, K.; Blanco, F.; Jones, D.B.; Brunger, M.J.; García, G. Total cross section of furfural by electron impact: Experiment and theory. J. Chem. Phys. 2017, 147, 054301. [Google Scholar] [CrossRef]
- Ren, X.; Pflüger, T.; Weyland, M.; Baek, W.Y.; Rabus, H.; Ullrich, J.; Dorn, A. An (e, 2e + ion) study of low-energy electron-impact ionization and fragmentation of tetrahydrofuran with high mass and energy resolutions. J. Chem. Phys. 2014, 141, 134314. [Google Scholar] [CrossRef]
- Costa, R.F.; Varella, M.T.d.N.; Bettega, M.H.F.; Lima, M.A.P. Recent Advances in the application of the Schwinger multichannel method with pseudopotentials to electron-molecule collisions. Eur. Phys. J. D 2015, 69, 159. [Google Scholar] [CrossRef] [Green Version]
- Blanco, F.; García, G. Improvements on the quasifree absorption model for electron scattering. Phys. Rev. A 2003, 67, 022701. [Google Scholar] [CrossRef] [Green Version]
- Sanz, A.G.; Fuss, M.C.; Blanco, F.; Sebastianelli, F.; Gianturco, F.A.; García, G. Electron scattering cross sections from HCN over a broad energy range (0.1–10 000 eV): Influence of the permanent dipole moment on the scattering process. J. Chem. Phys. 2012, 137, 124103. [Google Scholar] [CrossRef] [PubMed] [Green Version]



 , present experimental data [3];
, present experimental data [3];  , experimental data from [14];
, experimental data from [14];  , experimental data from [14] including the correction for rotational excitations into the acceptance angle of the detector (“missing angles”); ― integral elastic cross section calculated with the SMC method; ―, integral elastic cross section calculated with the R-matrix method; ―, integral elastic cross section calculated with the IAM-SCAR method; ---, our experimental data [3] including the correction for electrons elastically scattered into the “missing angles” as calculated with the IAM-SCAR differential elastic cross sections. -.-.; our experimental data [3] including both the corrections for elastic and rotational excitation scattered electrons into the “missing angles”.
, experimental data from [14] including the correction for rotational excitations into the acceptance angle of the detector (“missing angles”); ― integral elastic cross section calculated with the SMC method; ―, integral elastic cross section calculated with the R-matrix method; ―, integral elastic cross section calculated with the IAM-SCAR method; ---, our experimental data [3] including the correction for electrons elastically scattered into the “missing angles” as calculated with the IAM-SCAR differential elastic cross sections. -.-.; our experimental data [3] including both the corrections for elastic and rotational excitation scattered electrons into the “missing angles”.
 , present experimental data [3];
, present experimental data [3];  , experimental data from [14];
, experimental data from [14];  , experimental data from [14] including the correction for rotational excitations into the acceptance angle of the detector (“missing angles”); ― integral elastic cross section calculated with the SMC method; ―, integral elastic cross section calculated with the R-matrix method; ―, integral elastic cross section calculated with the IAM-SCAR method; ---, our experimental data [3] including the correction for electrons elastically scattered into the “missing angles” as calculated with the IAM-SCAR differential elastic cross sections. -.-.; our experimental data [3] including both the corrections for elastic and rotational excitation scattered electrons into the “missing angles”.
, experimental data from [14] including the correction for rotational excitations into the acceptance angle of the detector (“missing angles”); ― integral elastic cross section calculated with the SMC method; ―, integral elastic cross section calculated with the R-matrix method; ―, integral elastic cross section calculated with the IAM-SCAR method; ---, our experimental data [3] including the correction for electrons elastically scattered into the “missing angles” as calculated with the IAM-SCAR differential elastic cross sections. -.-.; our experimental data [3] including both the corrections for elastic and rotational excitation scattered electrons into the “missing angles”.
 , experimental data [3] including electrons elastically scattered into the “missing” angles (see text for details);
, experimental data [3] including electrons elastically scattered into the “missing” angles (see text for details);  , IECS based on the present R-matrix and IAM-SCAR calculations;
, IECS based on the present R-matrix and IAM-SCAR calculations;  , ionization;
, ionization;  , electronic excitation;
, electronic excitation;  , vibrational excitation;
, vibrational excitation;  , electron attachment;
, electron attachment;  , dipole-Born rotational excitation.
, dipole-Born rotational excitation.
 , experimental data [3] including electrons elastically scattered into the “missing” angles (see text for details);
, experimental data [3] including electrons elastically scattered into the “missing” angles (see text for details);  , IECS based on the present R-matrix and IAM-SCAR calculations;
, IECS based on the present R-matrix and IAM-SCAR calculations;  , ionization;
, ionization;  , electronic excitation;
, electronic excitation;  , vibrational excitation;
, vibrational excitation;  , electron attachment;
, electron attachment;  , dipole-Born rotational excitation.
, dipole-Born rotational excitation.





| E(eV) | IECS R-Matrix [1] | Electron Attachment | Electronic Excitation | Vibrational Excitation | Ionization | Rotational Excitation |
|---|---|---|---|---|---|---|
| 0.11 | 423 | 1374 | ||||
| 0.135 | 340 | 1145 | ||||
| 0.16 | 284.1 | 984.4 | ||||
| 0.185 | 244.1 | 864.9 | ||||
| 0.21 | 214.1 | 772.5 | ||||
| 0.235 | 190.8 | 698.8 | ||||
| 0.26 | 172.3 | 638.6 | ||||
| 0.285 | 157.2 | 588.5 | ||||
| 0.31 | 144.8 | 546 | ||||
| 0.335 | 134.3 | 509.5 | ||||
| 0.36 | 125.3 | 477.8 | ||||
| 0.385 | 117.6 | 450.1 | ||||
| 0.41 | 110.9 | 425.6 | ||||
| 0.435 | 105.1 | 403.7 | ||||
| 0.46 | 99.89 | 384.1 | ||||
| 0.485 | 95.27 | 366.4 | ||||
| 0.51 | 91.14 | 350.3 | ||||
| 0.535 | 87.42 | 335.7 | ||||
| 0.56 | 84.05 | 322.3 | ||||
| 0.585 | 80.99 | 310 | ||||
| 0.61 | 78.18 | 298.7 | ||||
| 0.635 | 75.61 | 288.2 | ||||
| 0.66 | 73.23 | 278.4 | ||||
| 0.685 | 71.06 | 269.3 | ||||
| 0.71 | 69.23 | <0.1 | 260.9 | |||
| 0.735 | 68.64 | 0.1459 | 252.9 | |||
| 0.76 | 67.39 | 18.25 | 245.5 | |||
| 0.785 | 66.19 | 29.47 | 238.5 | |||
| 0.81 | 65.01 | 7.442 | 232 | |||
| 0.835 | 63.87 | 3.107 | 225.8 | |||
| 0.86 | 62.77 | 1.479 | 219.9 | |||
| 0.885 | 61.7 | 0.6735 | 214.4 | |||
| 0.91 | 60.67 | 0.2315 | 209.1 | |||
| 0.935 | 59.66 | <0.1 | 204.1 | |||
| 0.96 | 58.61 | 199.4 | ||||
| 0.985 | 57.72 | 194.9 | ||||
| 1 | 57.21 | 192.2 | ||||
| 1.01 | 56.88 | 0.1512 | 190.6 | |||
| 1.03 | 56.02 | 0.6431 | 186.4 | |||
| 1.06 | 55.2 | 1.899 | 182.5 | |||
| 1.08 | 54.4 | 6.533 | 178.8 | |||
| 1.11 | 53.65 | 36.67 | 175.2 | |||
| 1.13 | 52.93 | 9.549 | 171.7 | |||
| 1.16 | 52.25 | 1.578 | 168.4 | |||
| 1.18 | 51.59 | 0.184 | 165.3 | |||
| 1.2 | 51.09 | <0.1 | 163.4 | |||
| 1.5 | 45.51 | 133.9 | ||||
| 1.7 | 43.42 | 119.8 | ||||
| 2 | 41.37 | <0.1 | 103.6 | |||
| 2.3 | 40.23 | 1.73 | 91.51 | |||
| 2.6 | 39.64 | 3.26 | 82.04 | |||
| 2.8 | 39.44 | 4.71 | 76.8 | |||
| 3 | 39.33 | 2.05 | 72.22 | |||
| 3.2 | 39.31 | <0.1 | 68.18 | |||
| 3.5 | 39.34 | <0.1 | 62.95 | |||
| 3.7 | 39.4 | 2.47 | 59.91 | |||
| 4 | 39.51 | 7.53 | 55.89 | |||
| 4.2 | 39.6 | 12.32 | 53.51 | |||
| 4.4 | 39.73 | 14.27 | 51.33 | |||
| 4.6 | 39.9 | 16.33 | 49.34 | |||
| 4.8 | 40.18 | 14.03 | 47.5 | |||
| 5 | 40.77 | 11.25 | 45.81 | |||
| 5.2 | 42.28 | 5.26 | 44.23 | |||
| 5.5 | 48.05 | 1.99 | 42.08 | |||
| 5.8 | 44.2 | 8.13 | 40.13 | |||
| 6 | 42.52 | 9.65 | 38.94 | |||
| 6.5 | 41.8 | 13.83 | 36.26 | |||
| 7 | 42.21 | 17.40 | 33.94 | |||
| 7.5 | 41.79 | 15.01 | 31.91 | |||
| 8 | 45.49 | 11.82 | 30.13 | |||
| 8.5 | 47.75 | 14.18 | 28.55 | |||
| 9 | 47.94 | 12.21 | 27.13 | |||
| 9.5 | 51.54 | 8.65 | 25.85 | |||
| 10 | 49.32 | 12.27 | <0.1 | 24.7 | ||
| 12 | 45.19 | 12.43 | 0.18 | 20.99 | ||
| 15 | 40.6 | 14.83 | 1.329 | 17.21 | ||
| 20 | 42.28 | 7.548 | 4.012 | 13.32 | ||
| 30 | 35.56 | 6.392 | 8.778 | 9.277 | ||
| 40 | 31.64 | 5.13 | 10.97 | 7.179 | ||
| 50 | 28.84 | 5.71 | 11.81 | 5.884 | ||
| 70 | 24.92 | 3.96 | 12.27 | 4.36 | ||
| 90 | 22.4 | 4.10 | 12.59 | 3.485 | ||
| 100 | 21.42 | 3.96 | 12.26 | 3.173 |
| E (eV) | IECS (10−20 m2) | E (eV) | IECS (10−20 m2) |
|---|---|---|---|
| 0.1 | 172.4 | 4.1 | 35.58 |
| 0.2 | 97.4 | 4.2 | 35.86 |
| 0.3 | 65.32 | 4.3 | 36.14 |
| 0.4 | 50.62 | 4.4 | 36.62 |
| 0.5 | 42.81 | 4.5 | 36.73 |
| 0.6 | 37.78 | 4.6 | 37.05 |
| 0.7 | 34.31 | 4.7 | 37.58 |
| 0.8 | 32.47 | 4.8 | 37.96 |
| 0.9 | 81.96 | 4.9 | 38.38 |
| 1 | 34.43 | 5 | 38.87 |
| 1.1 | 30.87 | 5.1 | 39.47 |
| 1.2 | 30.44 | 5.2 | 40.2 |
| 1.3 | 44.29 | 5.3 | 41.04 |
| 1.33 | 64.7 | 5.4 | 42.3 |
| 1.4 | 34.02 | 5.5 | 43.94 |
| 1.5 | 29.95 | 5.6 | 45.72 |
| 1.6 | 29.33 | 5.7 | 47.19 |
| 1.7 | 29.17 | 5.8 | 47.82 |
| 1.8 | 29.14 | 5.9 | 47.98 |
| 1.9 | 29.2 | 6 | 47.16 |
| 2 | 29.31 | 6.1 | 46.48 |
| 2.1 | 29.49 | 6.2 | 45.63 |
| 2.2 | 29.72 | 6.3 | 45.94 |
| 2.3 | 29.98 | 6.4 | 45.94 |
| 2.4 | 30.29 | 6.5 | 45.76 |
| 2.5 | 30.62 | 6.6 | 47.07 |
| 2.6 | 30.97 | 6.7 | 47.49 |
| 2.7 | 31.34 | 6.8 | 48.26 |
| 2.8 | 31.71 | 6.9 | 49.14 |
| 2.9 | 32.08 | 7 | 49.62 |
| 3 | 32.46 | 7.5 | 49.71 |
| 3.1 | 32.83 | 8 | 48.35 |
| 3.2 | 33.19 | 9 | 53.61 |
| 3.3 | 33.54 | 9.5 | 53.28 |
| 3.4 | 33.89 | 10 | 54.85 |
| 3.5 | 34.19 | 11 | 56.67 |
| 3.6 | 34.39 | 12 | 52.58 |
| 3.7 | 34.64 | 15 | 43.31 |
| 3.8 | 34.92 | 16 | 46.12 |
| 3.9 | 35.2 | 18 | 39.85 |
| 4 | 35.74 | 20 | 36.35 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costa, F.; Traoré-Dubuis, A.; Álvarez, L.; Lozano, A.I.; Ren, X.; Dorn, A.; Limão-Vieira, P.; Blanco, F.; Oller, J.C.; Muñoz, A.; et al. A Complete Cross Section Data Set for Electron Scattering by Pyridine: Modelling Electron Transport in the Energy Range 0–100 eV. Int. J. Mol. Sci. 2020, 21, 6947. https://doi.org/10.3390/ijms21186947
Costa F, Traoré-Dubuis A, Álvarez L, Lozano AI, Ren X, Dorn A, Limão-Vieira P, Blanco F, Oller JC, Muñoz A, et al. A Complete Cross Section Data Set for Electron Scattering by Pyridine: Modelling Electron Transport in the Energy Range 0–100 eV. International Journal of Molecular Sciences. 2020; 21(18):6947. https://doi.org/10.3390/ijms21186947
Chicago/Turabian StyleCosta, Filipe, Ali Traoré-Dubuis, Lidia Álvarez, Ana I. Lozano, Xueguang Ren, Alexander Dorn, Paulo Limão-Vieira, Francisco Blanco, Juan C. Oller, Antonio Muñoz, and et al. 2020. "A Complete Cross Section Data Set for Electron Scattering by Pyridine: Modelling Electron Transport in the Energy Range 0–100 eV" International Journal of Molecular Sciences 21, no. 18: 6947. https://doi.org/10.3390/ijms21186947
APA StyleCosta, F., Traoré-Dubuis, A., Álvarez, L., Lozano, A. I., Ren, X., Dorn, A., Limão-Vieira, P., Blanco, F., Oller, J. C., Muñoz, A., García-Abenza, A., Gorfinkiel, J. D., Barbosa, A. S., Bettega, M. H. F., Stokes, P., White, R. D., Jones, D. B., Brunger, M. J., & García, G. (2020). A Complete Cross Section Data Set for Electron Scattering by Pyridine: Modelling Electron Transport in the Energy Range 0–100 eV. International Journal of Molecular Sciences, 21(18), 6947. https://doi.org/10.3390/ijms21186947