Revisiting the Interaction of Melittin with Phospholipid Bilayers: The Effects of Concentration and Ionic Strength
Abstract
:1. Introduction
2. Results
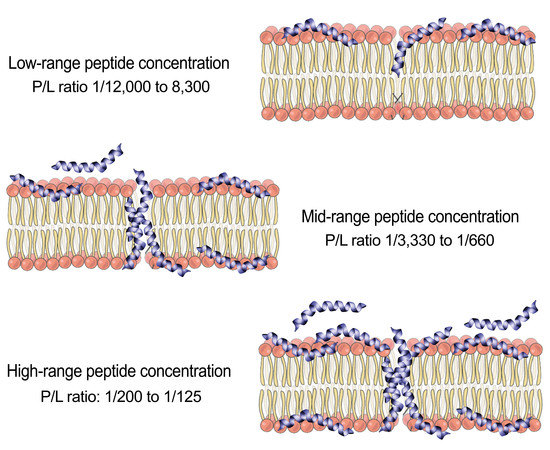
2.1. Effect of Analyte Concentration on Kinetics Analysis
2.2. Effects of NaCl on the Melittin–POPC Interaction
3. Discussion
4. Materials and Methods
4.1. Materials
4.2. Liposome Preparation
4.3. Surface Plasmon Resonance Experiments
4.3.1. Immobilization of POPC Vesicles on a L1 Chip
4.3.2. Binding experiments
4.4. Curve Fitting
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Breen, S.; Solomon, P.S.; Bedon, F.; Vincent, D. Surveying the potential of secreted antimicrobial peptides to enhance plant disease resistance. Front. Plant Sci. 2015, 6, 900. [Google Scholar] [CrossRef] [Green Version]
- Anaya-López, J.L.; López-Meza, J.E.; Ochoa-Zarzosa, A. Bacterial resistance to cationic antimicrobial peptides. Crit. Rev. Microbiol. 2013, 39, 180–195. [Google Scholar] [CrossRef] [PubMed]
- Brogden, N.K.; Brogden, K.A. Will new generations of modified antimicrobial peptides improve their potential as pharmaceuticals? Int. J. Antimicrob. Agents 2011, 38, 217–225. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guaní-Guerra, E.; Santos-Mendoza, T.; Lugo-Reyes, S.O.; Terán, L.M. Antimicrobial peptides: General overview and clinical implications in human health and disease. Clin. Immunol. 2010, 135, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Fjell, C.D.; Hiss, J.A.; Hancock, R.E.; Schneider, G. Designing antimicrobial peptides: form follows function. Nat. Rev. Drug Discov. 2011, 11, 37–51. [Google Scholar] [CrossRef]
- Schweizer, F. Cationic amphiphilic peptides with cancer-selective toxicity. Eur. J. Pharmacol. 2009, 625, 190–194. [Google Scholar] [CrossRef]
- Felício, M.R.; Silva, O.N.; Gonçalves, S.; Santos, N.C.; Franco, O.L. Peptides with Dual Antimicrobial and Anticancer Activities. Front. Chem. 2017, 5, 5. [Google Scholar] [CrossRef] [Green Version]
- Gaspar, D.; Veiga, A.S.; Castanho, M.A. From antimicrobial to anticancer peptides. A review. Front. Microbiol. 2013, 4, 294. [Google Scholar] [CrossRef] [Green Version]
- Leuschner, C.; Hansel, W. Membrane disrupting lytic peptides for cancer treatments. Curr. Pharm. Des. 2004, 10, 2299–2310. [Google Scholar] [CrossRef]
- Fernandez-Rojo, M.A.; Deplazes, E.; Pineda, S.S.; Brust, A.; Marth, T.; Wilhelm, P.; Martel, N.; Ramm, G.A.; Mancera, R.L.; Alewood, P.F.; et al. Gomesin peptides prevent proliferation and lead to the cell death of devil facial tumour disease cells. Cell Death Discov. 2018, 4, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Brogden, K.A. Antimicrobial peptides: pore formers or metabolic inhibitors in bacteria? Nat. Rev. Microbiol. 2005, 3, 238–250. [Google Scholar] [CrossRef] [PubMed]
- Sani, M.-A.; Separovic, F. How Membrane-Active Peptides Get into Lipid Membranes. Acc. Chem. Res. 2016, 49, 1130–1138. [Google Scholar] [CrossRef] [PubMed]
- Zasloff, M. Antimicrobial peptides of multicellular organisms. Nature 2002, 415, 389–395. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Wang, G. APD: the Antimicrobial Peptide Database. Nucleic Acids Res. 2004, 32, D590–D592. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, R.; Eckert, T.; Lutteke, T.; Hanstein, S.; Scheidig, A.; MJJBonvin, A.; ENifantiev, N.; Kozar, T.; Schauer, R.; Abdulaziz Enani, M.; et al. Structure-Function Relationships of Antimicrobial Peptides and Proteins with Respect to Contact Molecules on Pathogen Surfaces. Curr. Top. Med. Chem. 2016, 16, 89–98. [Google Scholar] [CrossRef] [PubMed]
- Raghuraman, H.; Chattopadhyay, A. Melittin: a Membrane-active Peptide with Diverse Functions. Biosci. Rep. 2007, 27, 189–223. [Google Scholar] [CrossRef]
- Habermann, E. Bee and Wasp Venoms. Science 1972, 177, 314–322. [Google Scholar] [CrossRef]
- Andersson, A.; Danielsson, J.; Gräslund, A.; Mäler, L. Kinetic models for peptide-induced leakage from vesicles and cells. Eur. Biophys. J. 2007, 36, 621–635. [Google Scholar] [CrossRef]
- Burton, M.G.; Huang, Q.M.; Hossain, M.A.; Wade, J.D.; Palombo, E.A.; Gee, M.L.; Clayton, A.H. Direct Measurement of Pore Dynamics and Leakage Induced by a Model Antimicrobial Peptide in Single Vesicles and Cells. Langmuir 2016, 32, 6496–6505. [Google Scholar] [CrossRef]
- Hur, J.; Kim, K.; Lee, S.; Park, H.; Park, Y. Melittin-induced alterations in morphology and deformability of human red blood cells using quantitative phase imaging techniques. Sci. Rep. 2017, 7, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Matsuzaki, K.; Yoneyama, S.; Miyajima, K. Pore formation and translocation of melittin. Biophys. J. 1997, 73, 831–838. [Google Scholar] [CrossRef] [Green Version]
- Oren, Z.; Shai, Y. Selective lysis of bacteria but not mammalian cells by diastereomers of melittin: structure-function study. Biochemistry 1997, 36, 1826–1835. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.; Khadka, N.K. Kinetic Defects Induced by Melittin in Model Lipid Membranes: A Solution Atomic Force Microscopy Study. J. Phys. Chem. B 2016, 120, 4625–4634. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rex, S. Pore formation induced by the peptide melittin in different lipid vesicle membranes. Biophys. Chem. 1996, 58, 75–85. [Google Scholar] [CrossRef]
- Rex, S.; Schwarz, G. Quantitative Studies on the Melittin-Induced Leakage Mechanism of Lipid Vesicles. Biochemistry 1998, 37, 2336–2345. [Google Scholar] [CrossRef] [PubMed]
- Van Den Bogaart, G.; Guzmán, J.V.; Mika, J.T.; Poolman, B. On the mechanism of pore formation by melittin. J. Biol. Chem. 2008, 283, 33854–33857. [Google Scholar] [CrossRef] [Green Version]
- Van Den Bogaart, G.; Mika, J.T.; Krasnikov, V.; Poolman, B. The Lipid Dependence of Melittin Action Investigated by Dual-Color Fluorescence Burst Analysis. Biophys. J. 2007, 93, 154–163. [Google Scholar] [CrossRef] [Green Version]
- Brown, L.R.; Braun, W.; Kumar, A.; Wüthrich, K. High resolution nuclear magnetic resonance studies of the conformation and orientation of melittin bound to a lipid-water interface. Biophys. J. 1982, 37, 319–328. [Google Scholar] [CrossRef] [Green Version]
- Brown, L.R.; Lauterwein, J.; Wüthrich, K. High-resolution 1H-NMR studies of self-aggregation of melittin in aqueous solution. Biochim. Biophys. Acta (BBA) Protein Struct. 1980, 622, 231–244. [Google Scholar] [CrossRef]
- Dawson, C.R.; Drake, A.F.; Helliwell, J.; Hider, R.C. The interaction of bee melittin with lipid bilayer membranes. Biochim. Biophys. Acta (BBA) Biomembr. 1978, 510, 75–86. [Google Scholar] [CrossRef]
- Ikura, T.; Gō, N.; Inagaki, F. Refined structure of melittin bound to perdeuterated dodeclylphoscholine micelles as studied by 2D-NMR and distance geometry calculation. Proteins Struct. Funct. Bioinform. 1991, 9, 81–89. [Google Scholar] [CrossRef] [PubMed]
- Ladokhin, A.S.; White, S.H. Folding of amphipathic α-helices on membranes: energetics of helix formation by melittin11Edited by D. Rees. J. Mol. Biol. 1999, 285, 1363–1369. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lam, Y.H.; Wassall, S.R.; Morton, C.J.; Smith, R.; Separovic, F. Solid-State NMR Structure Determination of Melittin in a Lipid Environment. Biophys. J. 2001, 81, 2752–2761. [Google Scholar] [CrossRef] [Green Version]
- Lauterwein, J.; Brown, L.R.; Wüthrich, K. High-resolution 1H-NMR studies of monomeric melittin in aqueous solution. Biochim. Biophys. Acta (BBA) Protein Struct. 1980, 622, 219–230. [Google Scholar] [CrossRef]
- Vogel, H. Incorporation of melittin into phosphatidylcholine bilayers. Study of binding and conformational changes. FEBS Lett. 1981, 134, 37–42. [Google Scholar] [CrossRef] [Green Version]
- Vogel, H. Comparison of the conformation and orientation of alamethicin and melittin in lipid membranes. Biochemistry 1987, 26, 4562–4572. [Google Scholar] [CrossRef]
- Hristova, K.; Dempsey, C.E.; White, S.H. Structure, location, and lipid perturbations of melittin at the membrane interface. Biophys. J. 2001, 80, 801–811. [Google Scholar] [CrossRef] [Green Version]
- Iwadate, M.; Asakura, T.; Williamson, M.P. The structure of the melittin tetramer at different temperatures. Eur. J. Biochem. 1998, 257, 479–487. [Google Scholar] [CrossRef]
- Park, S.C.; Kim, J.Y.; Shin, S.O.; Jeong, C.Y.; Kim, M.H.; Shin, S.Y.; Cheong, G.W.; Park, Y.; Hahm, K.S. Investigation of toroidal pore and oligomerization by melittin using transmission electron microscopy. Biochem. Biophys. Res. Commun. 2006, 343, 222–228. [Google Scholar] [CrossRef]
- Wimley, W.C. How Does Melittin Permeabilize Membranes? Biophys. J. 2018, 114, 251–253. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.W. Action of antimicrobial peptides: two-state model. Biochemistry 2000, 39, 8347–8352. [Google Scholar] [CrossRef] [PubMed]
- Terwilliger, T.C.; Eisenberg, D. The structure of melittin. J. Biol. Chem. 1982, 257, L6010–L6015. [Google Scholar]
- Berneche, S.; Nina, M.; Roux, B. Molecular dynamics simulation of melittin in a dimyristoylphosphatidylcholine bilayer membrane. Biophys. J. 1998, 75, 1603–1618. [Google Scholar] [CrossRef] [Green Version]
- Deplazes, E. Molecular simulations of venom peptide-membrane interactions: Progress and challenges. Pept. Sci. 2018, 110, e24060. [Google Scholar] [CrossRef]
- Irudayam, S.J.; Berkowitz, M.L. Binding and reorientation of melittin in a POPC bilayer: computer simulations. Biochim. Biophys. Acta 2012, 1818, 2975–2981. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Leveritt, J.M., III; Pino-Angeles, A.; Lazaridis, T. The Structure of a Melittin-Stabilized Pore. Biophys. J. 2015, 108, 2424–2426. [Google Scholar] [CrossRef] [Green Version]
- Lyu, Y.; Xiang, N.; Zhu, X.; Narsimhan, G. Potential of mean force for insertion of antimicrobial peptide melittin into a pore in mixed DOPC/DOPG lipid bilayer by molecular dynamics simulation. J. Chem. Phys. 2017, 146, 155101. [Google Scholar] [CrossRef]
- Upadhyay, S.K.; Wang, Y.; Zhao, T.; Ulmschneider, J.P. Insights from Micro-second Atomistic Simulations of Melittin in Thin Lipid Bilayers. J. Membr. Biol. 2015, 248, 497–503. [Google Scholar] [CrossRef]
- Huang, H.W. Elasticity of lipid bilayer interacting with amphiphilic helical peptides. J. Phys. II 1995, 5, 1427–1431. [Google Scholar] [CrossRef]
- Chen, L.Y.; Cheng, C.W.; Lin, J.J.; Chen, W.Y. Exploring the effect of cholesterol in lipid bilayer membrane on the melittin penetration mechanism. Anal. Biochem. 2007, 367, 49–55. [Google Scholar] [CrossRef]
- Dufourcq, J.; Faucon, J.F. Intrinsic fluorescence study of lipid-protein interactions in membrane models. Binding of melittin, an amphipathic peptide, to phospholipid vesicles. Biochim. Biophys. Acta (BBA) Biomembr. 1977, 467, 1–11. [Google Scholar] [CrossRef]
- Ghosh, A.K.; Rukmini, R.; Chattopadhyay, A. Modulation of tryptophan environment in membrane-bound melittin by negatively charged phospholipids: implications in membrane organization and function. Biochemistry 1997, 36, 14291–14305. [Google Scholar] [CrossRef] [PubMed]
- Strömstedt, A.A.; Wessman, P.; Ringstad, L.; Edwards, K.; Malmsten, M. Effect of lipid headgroup composition on the interaction between melittin and lipid bilayers. J. Colloid Interface Sci. 2007, 311, 59–69. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.T.; Sun, T.L.; Hung, W.C.; Huang, H.W. Process of inducing pores in membranes by melittin. Proc. Natl. Acad. Sci. USA 2013, 110, 14243–14248. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Allende, D.; Simon, S.; McIntosh, T.J. Melittin-induced bilayer leakage depends on lipid material properties: evidence for toroidal pores. Biophys. J. 2005, 88, 1828–1837. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ladokhin, A.S.; White, S.H. ‘Detergent-like’permeabilization of anionic lipid vesicles by melittin. Biochim. Biophys. Acta (BBA) Biomembr. 2001, 1514, 253–260. [Google Scholar] [CrossRef] [Green Version]
- Benachir, T.; Lafleur, M. Study of vesicle leakage induced by melittin. Biochim. Biophys. Acta 1995, 1235, 452–460. [Google Scholar] [CrossRef] [Green Version]
- Hincha, D.K.; Crowe, J.H. The lytic activity of the bee venom peptide melittin is strongly reduced by the presence of negatively charged phospholipids or chloroplast galactolipids in the membranes of phosphatidylcholine large unilamellar vesicles. Biochim. Biophys. Acta (BBA) Biomembr. 1996, 1284, 162–170. [Google Scholar] [CrossRef] [Green Version]
- Allende, D.; McIntosh, T.J. Lipopolysaccharides in Bacterial Membranes Act like Cholesterol in Eukaryotic Plasma Membranes in Providing Protection against Melittin-Induced Bilayer Lysis. Biochemistry 2003, 42, 1101–1108. [Google Scholar] [CrossRef]
- Beschiaschvili, G.; Seelig, J. Melittin binding to mixed phosphatidylglycerol/phosphatidylcholine membranes. Biochemistry 1990, 29, 52–58. [Google Scholar] [CrossRef]
- Klocek, G.; Schulthess, T.; Shai, Y.; Seelig, J. Thermodynamics of melittin binding to lipid bilayers. Aggregation and pore formation. Biochemistry 2009, 48, 2586–2596. [Google Scholar] [CrossRef] [PubMed]
- Hall, K.; Lee, T.H.; Aguilar, M.I. The role of electrostatic interactions in the membrane binding of melittin. J. Mol. Recognit. 2011, 24, 108–118. [Google Scholar] [CrossRef] [PubMed]
- Hall, K.; Mozsolits, H.; Aguilar, M.I. Surface plasmon resonance analysis of antimicrobial peptide-membrane interactions: affinity & mechanism of action. Lett. Pept. Sci. 2003, 10, 475–485. [Google Scholar]
- Lee, T.H.; Mozsolits, H.; Aguilar, M.I. Measurement of the affinity of melittin for zwitterionic and anionic membranes using immobilized lipid biosensors. J. Pept. Res. 2001, 58, 464–476. [Google Scholar] [CrossRef]
- Mozsolits, H.; Wirth, H.J.; Werkmeister, J.; Aguilar, M.I. Analysis of antimicrobial peptide interactions with hybrid bilayer membrane systems using surface plasmon resonance. Biochim. Biophys. Acta (BBA) Biomembr. 2001, 1512, 64–76. [Google Scholar] [CrossRef] [Green Version]
- Bhunia, A.; Domadia, P.N.; Bhattacharjya, S. Structural and thermodynamic analyses of the interaction between melittin and lipopolysaccharide. Biochim. Biophys. Acta (BBA) Biomembr. 2007, 1768, 3282–3291. [Google Scholar] [CrossRef] [Green Version]
- Henriksen, J.R.; Andresen, T.L. Thermodynamic profiling of peptide membrane interactions by isothermal titration calorimetry: a search for pores and micelles. Biophys. J. 2011, 101, 100–109. [Google Scholar] [CrossRef] [Green Version]
- Papo, N.; Shai, Y. Exploring peptide membrane interaction using surface plasmon resonance: differentiation between pore formation versus membrane disruption by lytic peptides. Biochemistry 2003, 42, 458–466. [Google Scholar] [CrossRef]
- Bello, J.; Bello, H.R.; Granados, E. Conformation and aggregation of melittin: dependence of pH and concentration. Biochemistry 1982, 21, 461–465. [Google Scholar] [CrossRef]
- Raghuraman, H.; Chattopadhyay, A. Effect of ionic strength on folding and aggregation of the hemolytic peptide melittin in solution. Biopolym. Orig. Res. Biomol. 2006, 83, 111–121. [Google Scholar] [CrossRef]
- Talbot, J.C.; Dufourcq, J.; De Bony, J.; Faucon, J.F.; Lussan, C. Conformational change and self association of monomeric melittin. FEBS Lett. 1979, 102, 191–193. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Choi, H.; Weisshaar, J.C. Melittin-induced permeabilization, re-sealing, and re-permeabilization of E. coli membranes. Biophys. J. 2018, 114, 368–379. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shai, Y.; Oren, Z. From “carpet” mechanism to de-novo designed diastereomeric cell-selective antimicrobial peptides. Peptides 2001, 22, 1629–1641. [Google Scholar] [CrossRef]
- Crescenzo, D.; Grothe, S.; Lortie, R.; Debanne, M.T.; OʹConnor-McCourt, M. Real-time kinetic studies on the interaction of transforming growth factor alpha with the epidermal growth factor receptor extracellular domain reveal a conformational change model. Biochemistry 2000, 39, 9466–9476. [Google Scholar] [CrossRef] [PubMed]
- Walkenhorst, W.F. Using adjuvants and environmental factors to modulate the activity of antimicrobial peptides. Biochim. Biophys. Acta (BBA) Biomembr. 2016, 1858, 926–935. [Google Scholar] [CrossRef] [PubMed]
- Santos, N.C.; Prieto, M.; Castanho, M.A.R.B. Quantifying molecular partition into model systems of biomembranes: an emphasis on optical spectroscopic methods. Biochim. Biophys. Acta (BBA) Biomembr. 2003, 1612, 123–135. [Google Scholar] [CrossRef] [Green Version]
- Domingues, T.M.; Mattei, B.; Seelig, J.; Perez, K.R.; Miranda, A.; Riske, K.A. Interaction of the antimicrobial peptide gomesin with model membranes: a calorimetric study. Langmuir 2013, 29, 8609–8618. [Google Scholar] [CrossRef]
- Beschiaschvili, G.; Baeuerle, H.-D. Effective charge of melittin upon interaction with POPC vesicles. Biochim. Biophys. Acta (BBA) Biomembr. 1991, 1068, 195–200. [Google Scholar] [CrossRef]
- Yuan, J.; Wu, Y.; Aguilar, M.-I. Surface Plasmon Resonance Spectroscopy in the Biosciences. In Amino Acids, Peptides and Proteins in Organic Chemistry; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2011; pp. 225–247. [Google Scholar]
- Kuchinka, E.; Seelig, J. Interaction of melittin with phosphatidylcholine membranes. Binding isotherm and lipid head-group conformation. Biochemistry 1989, 28, 4216–4221. [Google Scholar] [CrossRef]
- Yang, L.; Harroun, T.A.; Weiss, T.M.; Ding, L.; Huang, H.W. Barrel-stave model or toroidal model? A case study on melittin pores. Biophys. J. 2001, 81, 1475–1485. [Google Scholar] [CrossRef] [Green Version]
- Woo, S.Y.; Lee, H. Aggregation and insertion of melittin and its analogue MelP5 into lipid bilayers at different concentrations: effects on pore size, bilayer thickness and dynamics. Phys. Chem. Chem. Phys. 2017, 19, 7195–7203. [Google Scholar] [CrossRef] [PubMed]
- Wheaten, S.A.; Ablan, F.D.; Spaller, B.L.; Trieu, J.M.; Almeida, P.F. Translocation of Cationic Amphipathic Peptides across the Membranes of Pure Phospholipid Giant Vesicles. J. Am. Chem. Soc. 2013, 135, 16517–16525. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wiedman, G.; Herman, K.; Searson, P.; Wimley, W.C.; Hristova, K. The electrical response of bilayers to the bee venom toxin melittin: Evidence for transient bilayer permeabilization. Biochim. Biophys. Acta (BBA) Biomembr. 2013, 1828, 1357–1364. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Irudayam, S.J.; Pobandt, T.; Berkowitz, M.L. Free energy barrier for melittin reorientation from a membrane-bound state to a transmembrane state. J. Phys. Chem. B 2013, 117, 13457–13463. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Deplazes, E.; White, J.; Murphy, C.; Cranfield, C.G.; Garcia, A. Competing for the same space: protons and alkali ions at the interface of phospholipid bilayers. Biophys. Rev. 2019, 11, 483–490. [Google Scholar] [CrossRef]
- Tatulian, S.A. Binding of alkaline-earth metal cations and some anions to phosphatidylcholine liposomes. Eur. J. Biochem. 1987, 170, 413–420. [Google Scholar] [CrossRef]
- Ong, S.G.M.; Chitneni, M.; Lee, K.S.; Ming, L.C.; Yuen, K.H. Evaluation of extrusion technique for nanosizing liposomes. Pharmaceutics 2016, 8, 36. [Google Scholar] [CrossRef]
- Karlsson, R.; Katsamba, P.S.; Nordin, H.; Pol, E.; Myszka, D.G. Analyzing a kinetic titration series using affinity biosensors. Anal. Biochem. 2006, 349, 136–147. [Google Scholar] [CrossRef]





| Analyte (Melittin) Concentration (µM) | ka (M−1·s−1) | kd (M−1·s−1) | KD (M) | Rmax (RU) | Chi2 (RU) | U-Value |
|---|---|---|---|---|---|---|
| 0.5–8.0 (high-range) | 2.2 ± 0.1 × 103 | 2.7 ± 0.1 × 10−3 | 1.2 ± 0.1 × 10−6 | 2841 ± 24 | 192 | 12 |
| 0.5–8.0 (high-range) +0.15 M NaCl | 1.1 ± 0.3 × 103 | 8.2 ± 1.1 × 10−4 | 0.6 ± 0.3 × 10−6 | 2168 ± 28 | 198 | 12 |
| 0.3–1.5 (mid-range) | 1.6 ± 0.2 × 104 | 7.4 ± 0.2 × 10−4 | 4.1 ± 0.1 × 10−8 | 216 ± 11 | 12 | 9 |
| 0.04–0.12 (low-range) | 1.2 ± 0.3 × 105 | 5.7 ± 0.8 × 10−4 | 4.7 ± 0.6 × 10−9 | 197 ± 8 | 7 | 5 |
| Analyte (Melittin) Concentration (µM) | ka1 (M−1·s−1) | kd1 (s−1) | ka2 (M−1·s−1) | kd2 (s−1) | KD (M) | Rmax (RU) | Chi2 (RU) |
|---|---|---|---|---|---|---|---|
| 0.5–8.0 (high-range) | 5.2 ± 0.1 ×103 | 4.7 ± 0.2 ×10−2 | 1.3 ± 0.01 ×10−2 | 3.1 ± 0.1 ×10−3 | 1.7 ± 0.2 ×10−6 | 3488 ± 48 | 134 |
| 0.5–8.0 (high-range) +0.15 M NaCl | 2.2 ± 0.6 ×104 | 5.8 ± 1.2 ×10−2 | 3.8 ± 1.1 ×10−3 | 8.5 ± 0.7 ×10−4 | 0.5 ± 0.2 ×10−6 | 2725 ± 18 | 122 |
| 0.3–1.5 (mid-range) | 4.6 ± 0.2 ×104 | 1.3 ± 0.1 ×10−2 | 3.4 ± 0.3 ×10−3 | 1.2 ± 0.3 ×10−6 | 1.5 ± 0.2 ×10−11 | 243 ± 13 | 7 |
| 0.04–0.12 (low-range) | 2.1 ± 0.1 ×105 | 7.1 ± 0.1 ×10−3 | 5.2 ± 0.4 ×10−3 | 2.2 ± 0.8 ×10−6 | 1.5 ± 0.3 ×10−11 | 200 ± 9 | 3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sabapathy, T.; Deplazes, E.; Mancera, R.L. Revisiting the Interaction of Melittin with Phospholipid Bilayers: The Effects of Concentration and Ionic Strength. Int. J. Mol. Sci. 2020, 21, 746. https://doi.org/10.3390/ijms21030746
Sabapathy T, Deplazes E, Mancera RL. Revisiting the Interaction of Melittin with Phospholipid Bilayers: The Effects of Concentration and Ionic Strength. International Journal of Molecular Sciences. 2020; 21(3):746. https://doi.org/10.3390/ijms21030746
Chicago/Turabian StyleSabapathy, Thiru, Evelyne Deplazes, and Ricardo L. Mancera. 2020. "Revisiting the Interaction of Melittin with Phospholipid Bilayers: The Effects of Concentration and Ionic Strength" International Journal of Molecular Sciences 21, no. 3: 746. https://doi.org/10.3390/ijms21030746
APA StyleSabapathy, T., Deplazes, E., & Mancera, R. L. (2020). Revisiting the Interaction of Melittin with Phospholipid Bilayers: The Effects of Concentration and Ionic Strength. International Journal of Molecular Sciences, 21(3), 746. https://doi.org/10.3390/ijms21030746