Advanced Methodology and Preliminary Measurements of Molecular and Mechanical Properties of Heart Valves under Dynamic Strain
Abstract
:1. Introduction
1.1. Heart Valve Tissue Organization
1.2. Heart Tissue Organization and Cardiac Injury
1.3. Data-Based Models for Diagnosis, Treatment and Prevention of Valve Injury
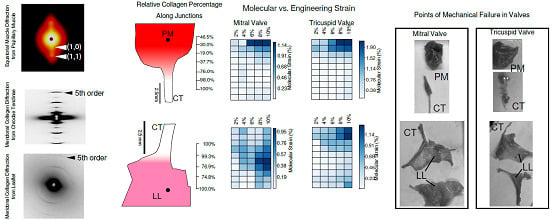
2. Results
2.1. Tissue Composition Along Transition Regions
2.2. Changes in Molecular vs. Engineering Strain with Application of Stretch to ‘Bisected’ Samples (Observations within Transition Regions)
2.3. Changes in Local Collagen Fiber Orientation in the LL–CT Junction with the Application of Stretch
2.4. Microscopic Evaluation of Stress and Strain on Individual Tissue Elements
2.5. Microscopic Evaluation of Stress and Strain in Bisected Samples
3. Discussion
4. Materials and Methods
4.1. Pig Heart Valve Priority and Dissection
4.2. Custom-Built Tissue Strain Apparatus
4.3. XRD Scanning to Determine Tissue Composition
4.4. XRD Scanning to Determine Molecular Strain with Application of Stretch
4.5. Microscopic Evaluation of Valve Components
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| PM | Papillary Muscle |
| CT | Chordae Tendinae |
| LL | Leaflet |
| MV | Mitral Valve |
| TV | Tricuspid Valve |
| AV | Aortic Valve |
| PG | Proteoglycan |
| XRD | X-ray Diffraction |
References
- Nkomo, V.T.; Gardin, J.M.; Skelton, T.N.; Gottdiener, J.S.; Scott, C.G.; Enriquez-Sarano, M. Burden of valvular heart diseases: A population-based study. Lancet 2006, 368, 1005–1011. [Google Scholar] [CrossRef]
- Vukanovic-Criley, J.M.; Criley, S.; Warde, C.M.; Boker, J.R.; Guevara-Matheus, L.; Churchill, W.H.; Nelson, W.P.; Criley, J.M. Competency in cardiac examination skills in medical students, trainees, physicians, and faculty: A multicenter study. Arch. Intern. Med. 2006, 166, 610–616. [Google Scholar] [CrossRef]
- Liao, J.; Vesely, I. Relationship between collagen fibrils, glycosaminoglycans, and stress relaxation in mitral valve chordae tendineae. Ann. Biomed. Eng. 2004, 32, 977–983. [Google Scholar] [CrossRef] [PubMed]
- Stephens, E.H.; de Jonge, N.; McNeill, M.P.; Durst, C.A.; Grande-Allen, K.J. Age-related changes in material behavior of porcine mitral and aortic valves and correlation to matrix composition. Tissue Eng. Part A 2009, 16, 867–878. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stephens, E.H.; Chu, C.K.; Grande-Allen, K.J. Valve proteoglycan content and glycosaminoglycan fine structure are unique to microstructure, mechanical load and age: Relevance to an age-specific tissue-engineered heart valve. Acta Biomater. 2008, 4, 1148–1160. [Google Scholar] [CrossRef] [PubMed]
- Herring, S.W.; Grimm, A.F.; Grimm, B.R. Regulation of sarcomere number in skeletal muscle: A comparison of hypotheses. Muscle Nerve 1984, 7, 161–173. [Google Scholar] [CrossRef]
- Vahl, C.; Lange, R.; Bauernschmitt, R.; Herold, U.; Tischmeyer, K.; Hagl, S. Analyzing Contractile Responses in Demembranized Pig Papillary Muscle Fibres: The Influence of Calcium, Resting Force, and Temperature. Thorac. Cardiovasc. Surg. 1991, 39, 329–337. [Google Scholar] [CrossRef]
- McDonald, K.S.; Hanft, L.M.; Domeier, T.L.; Emter, C.A. Length and PKA Dependence of Force Generation and Loaded Shortening in Porcine Cardiac Myocytes. Biochem. Res. Int. 2012, 2012, 1–12. [Google Scholar] [CrossRef] [Green Version]
- McCarthy, K.P.; Ring, L.; Rana, B.S. Anatomy of the mitral valve: Understanding the mitral valve complex in mitral regurgitation. Eur. Heart J. Cardiovasc. Imaging 2010, 11, i3–i9. [Google Scholar] [CrossRef] [Green Version]
- Nikolaou, P.K.; Macdonald, B.L.; Glisson, R.R.; Seaber, A.V.; Garrett, W.E., Jr. Biomechanical and histological evaluation of muscle after controlled strain injury. Am. J. Sports Med. 1987, 15, 9–14. [Google Scholar] [CrossRef]
- Delgado, G.J.; Chung, C.B.; Lektrakul, N.; Azocar, P.; Botte, M.J.; Coria, D.; Bosch, E.; Resnick, D. Tennis leg: Clinical US study of 141 patients and anatomic investigation of four cadavers with MR imaging and US. Radiology 2002, 224, 112–119. [Google Scholar] [CrossRef] [PubMed]
- Garrett, W.E.; Faherty, M.S. Muscle-Tendon Junction Injury. In Muscle and Tendon Injuries; Springer: Berlin, Germany, 2017; pp. 51–60. [Google Scholar]
- Madhurapantula, R.S.; Eidsmore, A.; Modrich, C.D.; Orgel, J.P. New Methodology and Preliminary Data in the Characterization of the Muscle Tendon Junction of Mammalian Muscle Tissues. EMS Eng. Sci. J. 2017, 1, 1–7. [Google Scholar]
- Abbasi, K.; Ahmadi, H.; Zoroufian, A.; Sahebjam, M.; Moshtaghi, N.; Abbasi, S.H. Post-traumatic chordae rupture of tricuspid valve. J. Tehran Univ. Heart Cent. 2012, 7, 185–187. [Google Scholar]
- Grenadier, E.; Keidar, S.; Sahn, D.; Alpan, G.; Goldberg, S.; Valdez Cruz, L.; LIMA, C.O.; Barron, J.; Allen, H.D.; Palant, A. Ruptured mitral chordae tendineae may be a frequent and insignificant complication in the mitral valve prolapse syndrome. Eur. Heart J. 1985, 6, 1006–1015. [Google Scholar] [CrossRef]
- Hammer, D.; Leier, C.V.; Baba, N.; Vasko, J.S.; Wooley, C.F.; Pinnell, S.R. Altered collagen composition in a prolapsing mitral valve with ruptured chordae tendineae. Am. J. Med. 1979, 67, 863–866. [Google Scholar] [CrossRef]
- Chandran, K.B. Role of computational simulations in heart valve dynamics and design of valvular prostheses. Cardiovasc. Eng. Technol. 2010, 1, 18–38. [Google Scholar] [CrossRef] [Green Version]
- Khalili, F.; Gamage, P.P.T.; Sandler, R.H.; Mansy, H.A. Adverse Hemodynamic Conditions Associated with Mechanical Heart Valve Leaflet Immobility. Bioengineering 2018, 5, 74. [Google Scholar] [CrossRef] [Green Version]
- Drach, A.; Khalighi, A.H.; Sacks, M.S. A comprehensive pipeline for multi-resolution modeling of the mitral valve: Validation, computational efficiency, and predictive capability. Int. J. Numer. Methods Biomed. Eng. 2018, 34, 2921. [Google Scholar] [CrossRef]
- Yoganathan, A.P.; He, Z.; Casey Jones, S. Fluid Mechanics of Heart Valves. Annu. Rev. Biomed. Eng. 2004, 6, 331–362. [Google Scholar] [CrossRef]
- Sacks, M.S.; David Merryman, W.; Schmidt, D.E. On the biomechanics of heart valve function. J. Biomech. 2009, 42, 1804–1824. [Google Scholar] [CrossRef] [Green Version]
- Labrosse, M.R.; Beller, C.J.; Boodhwani, M.; Hudson, C.; Sohmer, B. Subject-specific finite-element modeling of normal aortic valve biomechanics from 3D+t TEE images. Med Image Anal. 2015, 20, 162–172. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Martin, C.; Pham, T. Computational modeling of cardiac valve function and intervention. Annu. Rev. Biomed. Eng. 2014, 16, 53–76. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huxley, A.F.; Simmons, R.M. Proposed mechanism of force generation in striated muscle. Nature 1971, 233, 533–538. [Google Scholar] [CrossRef] [PubMed]
- Bosboom, E.; Hesselink, M.; Oomens, C.; Bouten, C.; Drost, M.; Baaijens, F. Passive transverse mechanical properties of skeletal muscle under in vivo compression. J. Biomech. 2001, 34, 1365–1368. [Google Scholar] [CrossRef]
- Buehler, M.J. Nanomechanics of collagen fibrils under varying cross-link densities: Atomistic and continuum studies. J. Mech. Behav. Biomed. Mater. 2008, 1, 59–67. [Google Scholar] [CrossRef] [PubMed]
- Hill, A.V. The heat of shortening and the dynamic constants of muscle. Proceedings of the Royal Society of London. Ser. B-Biol. Sci. 1938, 126, 136–195. [Google Scholar]
- Maceri, F.; Marino, M.; Vairo, G. An insight on multiscale tendon modeling in muscle–tendon integrated behavior. Biomech. Model. Mechanobiol. 2012, 11, 505–517. [Google Scholar] [CrossRef]
- Rehorn, M.R.; Blemker, S.S. The effects of aponeurosis geometry on strain injury susceptibility explored with a 3D muscle model. J. Biomech. 2010, 43, 2574–2581. [Google Scholar] [CrossRef] [Green Version]
- Shearer, T. A new strain energy function for modelling ligaments and tendons whose fascicles have a helical arrangement of fibrils. J. Biomech. 2015, 48, 3017–3025. [Google Scholar] [CrossRef]
- Spyrou, L.A.; Aravas, N. Muscle and tendon tissues: Constitutive modeling and computational issues. J. Appl. Mech. 2011, 78, 041015. [Google Scholar] [CrossRef] [Green Version]
- Roux, A.; Laporte, S.; Lecompte, J.; Gras, L.L.; Iordanoff, I. Influence of muscle-tendon complex geometrical parameters on modeling passive stretch behavior with the Discrete Element Method. J. Biomech. 2016, 49, 252–258. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sharafi, B.; Ames, E.G.; Holmes, J.W.; Blemker, S.S. Strains at the myotendinous junction predicted by a micromechanical model. J. Biomech. 2011, 44, 2795–2801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Orgel, J.; Madhurapantula, R.S.; Eidsmore, A.; Wang, M.; Dutov, P.; Modrich, C.D.; Antipova, O.; McDonald, J.; Satapathy, S. X-ray diffraction reveals blunt-force loading threshold for nanoscopic structural change in ex vivo neuronal tissues. J. Synchrotron Radiat. 2019, 26, 89–95. [Google Scholar] [CrossRef]
- Jiratrakanvong, J.; Shao, J.; Menendez, M.; Li, X.; Li, J.; Ma, W.; Agam, G.; Irving, T. MuscleX: Software Suite for Diffraction X-ray Imaging. 2018. Available online: https://zenodo.org/record/3360909#.Xin5McZKihc (accessed on 23 January 2020). [CrossRef]
- Orgel, J.P.; Irving, T.C.; Miller, A.; Wess, T.J. Microfibrillar structure of type I collagen in situ. Proc. Natl. Acad. Sci. USA 2006, 103, 9001–9005. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wess, T.J.; Orgel, J.P. Changes in collagen structure: Drying, dehydrothermal treatment and relation to long term deterioration. Thermochim. Acta 2000, 365, 119–128. [Google Scholar] [CrossRef]
- Orgel, J.P.; Persikov, A.V.; Antipova, O. Variation in the helical structure of native collagen. PLoS ONE 2014, 9, e89519. [Google Scholar] [CrossRef]
- Yagi, N.; Okuyama, H.; Toyota, H.; Araki, J.; Shimizu, J.; Iribe, G.; Nakamura, K.; Mohri, S.; Tsujioka, K.; Suga, H.; et al. Sarcomere-length dependence of lattice volume and radial mass transfer of myosin cross-bridges in rat papillary muscle. Pflügers Arch. 2004, 448, 153–160. [Google Scholar] [CrossRef]
- Rueden, C.T.; Schindelin, J.; Hiner, M.C.; DeZonia, B.E.; Walter, A.E.; Arena, E.T.; Eliceiri, K.W. ImageJ2: ImageJ for the next generation of scientific image data. BMC Bioinform. 2017, 18, 529. [Google Scholar] [CrossRef]
- Tinevez, J.Y.; Perry, N.; Schindelin, J.; Hoopes, G.M.; Reynolds, G.D.; Laplantine, E.; Bednarek, S.Y.; Shorte, S.L.; Eliceiri, K.W. TrackMate: An open and extensible platform for single-particle tracking. Methods 2017, 115, 80–90. [Google Scholar] [CrossRef]
- Oliveira, D.; Dawkins, K.; Kay, P.; Paneth, M. Chordal rupture. I: Aetiology and natural history. Heart 1983, 50, 312–317. [Google Scholar] [CrossRef] [Green Version]
- Gunning, G.M.; Murphy, B.P. Characterisation of the fatigue life, dynamic creep and modes of damage accumulation within mitral valve chordae tendineae. Acta Biomater. 2015, 24, 193–200. [Google Scholar] [CrossRef] [PubMed]
- Tidball, J.G. 12 Myotendinous Junction Injury in Relation to Junction Structure and Molecular Composition. Exerc. Sport Sci. Rev. 1991, 19, 419–446. [Google Scholar] [CrossRef] [PubMed]
- Jakobsen, J.R.; Mackey, A.; Knudsen, A.; Koch, M.; Kjaer, M.; Krogsgaard, M. Composition and adaptation of human myotendinous junction and neighboring muscle fibers to heavy resistance training. Scand. J. Med. Sci. Sports 2017, 27, 1547–1559. [Google Scholar] [CrossRef] [PubMed]
- Sturm, L.P.; Windsor, J.A.; Cosman, P.H.; Cregan, P.; Hewett, P.J.; Maddern, G.J. A systematic review of skills transfer after surgical simulation training. Ann. Surg. 2008, 248, 166–179. [Google Scholar] [CrossRef] [PubMed]
- Gomez, P.P.; Willis, R.E.; Van Sickle, K. Evaluation of two flexible colonoscopy simulators and transfer of skills into clinical practice. J. Surg. Educ. 2015, 72, 220–227. [Google Scholar] [CrossRef]








| Ultimate Stress (MPa) | ||
|---|---|---|
| Mitral Valve | Tricuspid Valve | |
| PM | 0.011 | 0.119 |
| PM–CT | 0.144 | 0.159 |
| CT | 1.491 | 4.503 |
| CT–LL | 0.024 | 0.097 |
| LL | 0.025 | 0.059 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Madhurapantula, R.S.; Krell, G.; Morfin, B.; Roy, R.; Lister, K.; Orgel, J.P.R.O. Advanced Methodology and Preliminary Measurements of Molecular and Mechanical Properties of Heart Valves under Dynamic Strain. Int. J. Mol. Sci. 2020, 21, 763. https://doi.org/10.3390/ijms21030763
Madhurapantula RS, Krell G, Morfin B, Roy R, Lister K, Orgel JPRO. Advanced Methodology and Preliminary Measurements of Molecular and Mechanical Properties of Heart Valves under Dynamic Strain. International Journal of Molecular Sciences. 2020; 21(3):763. https://doi.org/10.3390/ijms21030763
Chicago/Turabian StyleMadhurapantula, Rama S., Gabriel Krell, Berenice Morfin, Rajarshi Roy, Kevin Lister, and Joseph P.R.O. Orgel. 2020. "Advanced Methodology and Preliminary Measurements of Molecular and Mechanical Properties of Heart Valves under Dynamic Strain" International Journal of Molecular Sciences 21, no. 3: 763. https://doi.org/10.3390/ijms21030763
APA StyleMadhurapantula, R. S., Krell, G., Morfin, B., Roy, R., Lister, K., & Orgel, J. P. R. O. (2020). Advanced Methodology and Preliminary Measurements of Molecular and Mechanical Properties of Heart Valves under Dynamic Strain. International Journal of Molecular Sciences, 21(3), 763. https://doi.org/10.3390/ijms21030763