Structural Dynamics of C2F4I2 in Cyclohexane Studied via Time-Resolved X-ray Liquidography
Abstract
:1. Introduction
2. Results and Discussion
2.1. Time-Resolved Difference Scattering Curves of C2F4I2 Photodissociation
2.2. Determination of the Structure of the Radical Intermediate
2.3. Kinetics and Mechanism of C2F4I2 Photodissociation
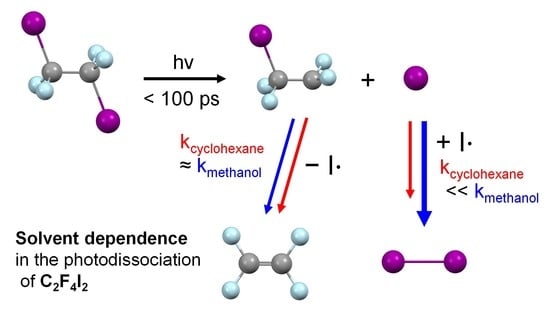
2.4. Solvent Dependence of Reaction Dynamics
2.4.1. Anti-to-Gauche Ratio of C2F4I·
2.4.2. Structural Conformation of C2F4I·
2.4.3. Secondary Dissociation Kinetics from C2F4I· to C2F4
2.4.4. Recombination Rate of Two I into I2
2.5. Various Types of Solvent Dependences
3. Materials and Methods
3.1. Time-Resolved X-ray Liquidography Experiment
3.2. Data Processing
3.3. Data Analysis
3.4. DFT Calculation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mulliken, R.S. Intensities in Molecular Electronic Spectra X. Calculations on Mixed-Halogen, Hydrogen Halide, Alkyl Halide, and Hydroxyl Spectra. J. Chem. Phys. 1940, 8, 382–395. [Google Scholar] [CrossRef]
- Kim, J.; Jun, S.; Kim, J.; Ihee, H. Density Functional and ab Initio Investigation of CF2ICF2I and CF2CF2I Radicals in Gas and Solution Phases. J. Phys. Chem. A 2009, 113, 11059–11066. [Google Scholar] [CrossRef] [PubMed]
- Kalume, A.; George, L.; Cunningham, N.; Reid, S.A. Case of the Missing Isomer: Pathways for Molecular Elimination in the Photoinduced Decomposition of 1,1-Dibromoethane. J. Phys. Chem. A 2013, 117, 11915–11923. [Google Scholar] [CrossRef]
- Kwok, W.M.; Ma, C.; Phillips, D.; Parker, A.W.; Towrie, M.; Matousek, P.; Phillips, D.L. Picosecond time-resolved resonance Raman observation of Iso-CH2Br–I following A-band photodissociation of CH 2BrI in the solution phase. Chem. Phys. Lett. 2001, 341, 292–298. [Google Scholar] [CrossRef]
- Lee, J.H.; Kim, J.; Cammarata, M.; Kong, Q.; Kim, K.H.; Choi, J.; Kim, T.K.; Wulff, M.; Ihee, H. Transient X-ray Diffraction Reveals Global and Major Reaction Pathways for the Photolysis of Iodoform in Solution. Angew. Chem. Int. Ed. 2008, 120, 1063–1066. [Google Scholar] [CrossRef]
- Davidsson, J.; Poulsen, J.; Cammarata, M.; Georgiou, P.; Wouts, R.; Katona, G.; Jacobson, F.; Plech, A.; Wulff, M.; Nyman, G.; et al. Structural Determination of a Transient Isomer of CH2I2 by Picosecond X-Ray Diffraction. Phys. Rev. Lett. 2005, 94, 245503. [Google Scholar] [CrossRef]
- Kong, Q.; Wulff, M.; Lee, J.H.; Bratos, S.; Ihee, H. Photochemical Reaction Pathways of Carbon Tetrabromide in Solution Probed by Picosecond X-ray Diffraction. J. Am. Chem. Soc. 2007, 129, 13584–13591. [Google Scholar] [CrossRef] [Green Version]
- Kong, Q.; Kim, J.; Lorenc, M.; Kim, T.K.; Ihee, H.; Wulff, M. Photodissociation Reaction of 1,2-Diiodoethane in Solution: A Theoretical and X-ray Diffraction Study. J. Phys. Chem. A 2005, 109, 10451–10458. [Google Scholar] [CrossRef]
- Lee, J.H.; Kim, T.K.; Kim, J.; Kong, Q.; Cammarata, M.; Lorenc, M.; Wulff, M.; Ihee, H. Capturing Transient Structures in the Elimination Reaction of Haloalkane in Solution by Transient X-ray Diffraction. J. Am. Chem. Soc. 2008, 130, 5834–5835. [Google Scholar] [CrossRef]
- Ihee, H.; Lorenc, M.; Kim, T.K.; Kong, Q.Y.; Cammarata, M.; Lee, J.H.; Bratos, S.; Wulff, M. Ultrafast X-ray Diffraction of Transient Molecular Structures in Solution. Science 2005, 309, 1223–1227. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ihee, H. Visualizing solution-phase reaction dynamics with time-resolved X-ray liquidography. Acc. Chem. Res. 2009, 42, 356–366. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Lee, J.H.; Kim, J.; Jun, S.; Kim, K.H.; Kim, T.W.; Wulff, M.; Ihee, H. Structural Dynamics of 1,2-Diiodoethane in Cyclohexane Probed by Picosecond X-ray Liquidography. J. Phys. Chem. A 2012, 116, 2713–2722. [Google Scholar] [CrossRef] [PubMed]
- Vincent, J.; Andersson, M.; Eklund, M.; Wöhri, A.B.; Odelius, M.; Malmerberg, E.; Kong, Q.; Wulff, M.; Neutze, R.; Davidsson, J. Solvent dependent structural perturbations of chemical reaction intermediates visualized by time-resolved x-ray diffraction. J. Chem. Phys. 2009, 130, 154502. [Google Scholar] [CrossRef]
- Marcellini, M.; Nasedkin, A.; Zietz, B.; Petersson, J.; Vincent, J.; Palazzetti, F.; Malmerberg, E.; Kong, Q.; Wulff, M.; van der Spoel, D. Transient isomers in the photodissociation of bromoiodomethane. J. Chem. Phys. 2018, 148, 134307. [Google Scholar] [CrossRef] [PubMed]
- Ahn, C.W.; Ki, H.; Kim, J.; Kim, J.; Park, S.; Lee, Y.; Kim, K.H.; Kong, Q.; Moon, J.; Pedersen, M.N. Direct observation of a transiently formed isomer during iodoform photolysis in solution by time-resolved X-ray liquidography. J. Phys. Chem. Lett. 2018, 9, 647–653. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Choi, J.; Ki, H.; Kim, K.H.; Oang, K.Y.; Roh, H.; Kim, J.; Nozawa, S.; Sato, T.; Adachi, S.-i. Fate of transient isomer of CH2I2: Mechanism and origin of ionic photoproducts formation unveiled by time-resolved x-ray liquidography. J. Chem. Phys. 2019, 150, 224201. [Google Scholar] [CrossRef]
- Gerck, E. Quantum yields of I (2P1/2) for CF3I, C2F5I, i-C3F7I, n-C3F7I, n-C6F13I, and 1, 2-C2F4I2 at 308 and 248 nm. J. Chem. Phys. 1983, 79, 311–315. [Google Scholar] [CrossRef]
- Thomassen, H.; Samdal, S.; Hedberg, K. Conformational analysis. 15. 1, 2-Dibromotetrafluoroethane and 1, 2-diiodotetrafluoroethane. Electron diffraction investigations of the molecular structures, compositions, and anti-gauche energy and entropy differences. J. Am. Chem. Soc. 1992, 114, 2810–2815. [Google Scholar] [CrossRef]
- Minton, T.K. Photofragmentation Dynamics of Iodohaloethanes. Ph.D. Thesis, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA, USA, 1986. [Google Scholar]
- Khundkar, L.R.; Zewail, A.H. Picosecond photofragment spectroscopy. IV. Dynamics of consecutive bond breakage in the reaction C2F4I2→ C2F4+ 2I. J. Chem. Phys. 1990, 92, 231–242. [Google Scholar] [CrossRef] [Green Version]
- Ihee, H.; Goodson, B.M.; Srinivasan, R.; Lobastov, V.A.; Zewail, A.H. Ultrafast Electron Diffraction and Structural Dynamics: Transient Intermediates in the Elimination Reaction of C2F4I2. J. Phys. Chem. A 2002, 106, 4087–4103. [Google Scholar] [CrossRef]
- Reckenthaeler, P.; Centurion, M.; Fuß, W.; Trushin, S.A.; Krausz, F.; Fill, E.E. Time-Resolved Electron Diffraction from Selectively Aligned Molecules. Phys. Rev. Lett. 2009, 102, 213001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wilkin, K.J.; Parrish, R.M.; Yang, J.; Wolf, T.J.; Nunes, J.P.F.; Guehr, M.; Li, R.; Shen, X.; Zheng, Q.; Wang, X. Diffractive imaging of dissociation and ground-state dynamics in a complex molecule. Phys. Rev. A 2019, 100, 023402. [Google Scholar] [CrossRef] [Green Version]
- Ihee, H.; Lobastov, V.A.; Gomez, U.M.; Goodson, B.M.; Srinivasan, R.; Ruan, C.-Y.; Zewail, A.H. Direct Imaging of Transient Molecular Structures with Ultrafast Diffraction. Science 2001, 291, 458–462. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ihee, H.; Kua, J.; Goddard, W.A.; Zewail, A.H. CF2XCF2X and CF2XCF2• Radicals (X = Cl, Br, I): Ab Initio and DFT Studies and Comparison with Experiments. J. Phys. Chem. A 2001, 105, 3623–3632. [Google Scholar] [CrossRef] [Green Version]
- Rasmusson, M.; Tarnovsky, A.N.; Pascher, T.; Sundström, V.; Åkesson, E. Photodissociation of CH2ICH2I, CF2ICF2I, and CF2BrCF2I in solution. J. Phys. Chem. A 2002, 106, 7090–7098. [Google Scholar] [CrossRef]
- Park, S.; Lee, T.; Shin, J.; Yoon, H.; Pak, Y.; Lim, M. Conformer-Specific Photodissociation Dynamics of CF2ICF2I in Solution Probed by Time-Resolved Infrared Spectroscopy. J. Phys. Chem. B 2020, 124, 8640–8650. [Google Scholar] [CrossRef]
- Tarnovsky, A.N.; Sundström, V.; Åkesson, E.; Pascher, T. Photochemistry of Diiodomethane in Solution Studied by Femtosecond and Nanosecond Laser Photolysis. Formation and Dark Reactions of the CH2I−I Isomer Photoproduct and Its Role in Cyclopropanation of Olefins. J. Phys. Chem. A 2004, 108, 237–249. [Google Scholar] [CrossRef]
- Zheng, X.; Kwok, W.M.; Phillips, D.L. Solvation Effects on the A-Band Photodissociation of Dibromomethane: Turning a Photodissociation into a Photoisomerization. J. Phys. Chem. A 2000, 104, 10464–10470. [Google Scholar] [CrossRef]
- Kong, Q.; Khakhulin, D.; Shkrob, I.A.; Lee, J.H.; Zhang, X.; Kim, J.; Kim, K.H.; Jo, J.; Kim, J.; Kang, J. Solvent-dependent complex reaction pathways of bromoform revealed by time-resolved X-ray solution scattering and X-ray transient absorption spectroscopy. Struct. Dyn. 2019, 6, 064902. [Google Scholar] [CrossRef]
- Haupa, K.A.; Lim, M.; Lee, Y.-P. Photodissociation of CF2ICF2I in solid para-hydrogen: Infrared spectra of anti- and gauche-˙C2F4I radicals. Phys. Chem. Chem. Phys. 2018, 20, 12650–12658. [Google Scholar] [CrossRef]
- Roeterdink, W.G.; Rijs, A.M.; Janssen, M.H.M. Imaging of Ultrafast Molecular Elimination Reactions. J. Am. Chem. Soc. 2006, 128, 576–580. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.-H.; Cheng, Y.-K.; Lee, Y.-P. Formation and Infrared Spectrum of the Open-Form 2-Bromoethyl Radical (2-C2H4Br•) from Ultraviolet Irradiation of a C2H4/Br2/p-H2 Matrix. J. Phys. Chem. A 2021, 125, 2139–2145. [Google Scholar] [CrossRef] [PubMed]
- Brum, J.L.; Deshmukh, S.; Wang, Z.; Koplitz, B. Site-specific branching ratios for H-atom production from primary haloalkanes photolyzed at 193, 222, and 248 nm. J. Chem. Phys. 1993, 98, 1178–1192. [Google Scholar] [CrossRef]
- Kwok, W.M.; Fuss, W.; Phillips, D.L. Bond selective electronic excitation in IC2H4C2F4I investigated by resonance Raman spectroscopy. Chem. Phys. Lett. 1996, 261, 685–690. [Google Scholar] [CrossRef]
- Man, S.Q.; Kwok, W.M.; Phillips, D.L.; Johnson, A.E. Short-time photodissociation dynamics of A-band and B-band bromoiodomethane in solution: An examination of bond selective electronic excitation. J. Chem. Phys. 1996, 105, 5842–5857. [Google Scholar] [CrossRef] [Green Version]
- Zheng, X.; Phillips, D.L. A-band resonance Raman spectra and short-time photodissociation dynamics of trans 1-chloro-2-iodoethane in cyclohexane solution. Chem. Phys. Lett. 1998, 286, 79–87. [Google Scholar] [CrossRef]
- Panman, M.R.; Biasin, E.; Berntsson, O.; Hermann, M.; Niebling, S.; Hughes, A.J.; Kübel, J.; Atkovska, K.; Gustavsson, E.; Nimmrich, A. Observing the Structural Evolution in the Photodissociation of Diiodomethane with Femtosecond Solution X-Ray Scattering. Phys. Rev. Lett. 2020, 125, 226001. [Google Scholar] [CrossRef]
- Park, S.; Shin, J.; Yoon, H.; Pak, Y.; Lim, M. Complete photodissociation dynamics of CF2I2 in solution. Phys. Chem. Chem. Phys. 2019, 21, 6859–6867. [Google Scholar] [CrossRef]
- Kim, H.; Kim, J.G.; Kim, T.W.; Lee, S.J.; Nozawa, S.; Adachi, S.-I.; Yoon, K.; Kim, J.; Ihee, H. Ultrafast structural dynamics of in-cage isomerization of diiodomethane in solution. Chem. Sci. 2021, 12, 2114–2120. [Google Scholar] [CrossRef] [PubMed]
- Butler, L.; Hintsa, E.; Shane, S.F.; Lee, Y.-T. The Electronic State-selective Photodissociation of CH2BrI at 248, 210, and 193 nm. J. Chem. Phys. 1987, 86, 2051–2074. [Google Scholar] [CrossRef] [Green Version]
- Lin, J.J.; Chen, Y.; Lee, Y.Y.; Lee, Y.T.; Yang, X. Photodissociation dynamics of CH3Cl at 157.6 nm: Evidence for CH2(X~3B1/a~1A1)+HCl product channels. Chem. Phys. Lett. 2002, 361, 374–382. [Google Scholar] [CrossRef]
- Odelius, M.; Kadi, M.; Davidsson, J.; Tarnovsky, A.N. Photodissociation of diiodomethane in acetonitrile solution and fragment recombination into iso-diiodomethane studied with ab initio molecular dynamics simulations. J. Chem. Phys. 2004, 121, 2208–2214. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Shin, J.; Yoon, H.; Lim, M. Photodissociation Dynamics of CF2I2 in CCl4 Solution Probed by Femtosecond Infrared Spectroscopy. Bull. Korean Chem. Soc. 2020, 41, 966–968. [Google Scholar] [CrossRef]
- Cox, A.P.; Duxbury, G.; Hardy, J.A.; Kawashima, Y. Microwave spectra of CF3Br and CF3I. Structures and dipole moments. J. Chem. Soc. Faraday Trans. 2 1980, 76, 339–350. [Google Scholar] [CrossRef]
- Engels, B.; Peyerimhoff, S.D. Theoretical study of the bridging in β-halo ethyl. J. Mol. Struct. 1986, 138, 59–68. [Google Scholar] [CrossRef] [Green Version]
- Zhong, D.; Ahmad, S.; Zewail, A. Femtosecond Elimination Reaction Dynamics. J. Am. Chem. Soc. 1997, 119, 5978–5979. [Google Scholar] [CrossRef]
- Ihee, H.; Zewail, A.H.; Goddard, W.A. Conformations and barriers of haloethyl radicals (CH2XCH2, X= F, Cl, Br, I): Ab initio studies. J. Phys. Chem. A 1999, 103, 6638–6649. [Google Scholar] [CrossRef] [Green Version]
- Skell, P.S.; Tuleen, D.L.; Readio, P.D. Stereochemical Evidence of Bridged Radicals. J. Am. Chem. Soc. 1963, 85, 2849–2850. [Google Scholar] [CrossRef]
- Skell, P.S.; Traynham, J.G. Radical brominations of alkyl bromides and the nature of β-bromoalkyl radicals. Acc. Chem. Res. 1984, 17, 160–166. [Google Scholar] [CrossRef]
- Kim, K.H.; Kim, J.; Lee, J.H.; Ihee, H. Topical Review: Molecular reaction and solvation visualized by time-resolved X-ray solution scattering: Structure, dynamics, and their solvent dependence. Struct. Dyn. 2014, 1, 011301. [Google Scholar] [CrossRef]
- Kim, T.K.; Lee, J.H.; Wulff, M.; Kong, Q.; Ihee, H. Spatiotemporal Kinetics in Solution Studied by Time-Resolved X-Ray Liquidography (Solution Scattering). ChemPhysChem 2009, 10, 1958–1980. [Google Scholar] [CrossRef]
- Kim, J.; Kim, K.H.; Oang, K.Y.; Lee, J.H.; Hong, K.; Cho, H.; Huse, N.; Schoenlein, R.W.; Kim, T.K.; Ihee, H. Tracking reaction dynamics in solution by pump–probe X-ray absorption spectroscopy and X-ray liquidography (solution scattering). Chem. Commun. 2016, 52, 3734–3749. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.H.; Wulff, M.; Bratos, S.; Petersen, J.; Guerin, L.; Leicknam, J.-C.; Cammarata, M.; Kong, Q.; Kim, J.; Møller, K.B. Filming the Birth of Molecules and Accompanying Solvent Rearrangement. J. Am. Chem. Soc. 2013, 135, 3255–3261. [Google Scholar] [CrossRef]
- Kim, T.K.; Lorenc, M.; Lee, J.H.; Russo, M.L.; Kim, J.; Cammarata, M.; Kong, Q.; Noel, S.; Plech, A.; Wulff, M. Spatiotemporal reaction kinetics of an ultrafast photoreaction pathway visualized by time-resolved liquid x-ray diffraction. Proc. Natl. Acad. Sci. USA 2006, 103, 9410–9415. [Google Scholar] [CrossRef] [Green Version]
- Leshchev, D.; Khakhulin, D.; Newby, G.; Ki, H.; Ihee, H.; Wulff, M. Sub-nanosecond secondary geminate recombination in mercury halides HgX2 (X = I, Br) investigated by time-resolved x-ray scattering. J. Chem. Phys. 2019, 151, 054310. [Google Scholar] [CrossRef]
- Choi, E.H.; Ahn, D.-S.; Park, S.; Kim, C.; Ahn, C.W.; Kim, S.; Choi, M.; Yang, C.; Kim, T.W.; Ki, H. Structural Dynamics of Bismuth Triiodide in Solution Triggered by Photoinduced Ligand-to-Metal Charge Transfer. J. Phys. Chem. Lett. 2019, 10, 1279–1285. [Google Scholar] [CrossRef] [PubMed]
- Kong, Q.; Lee, J.H.; Kim, K.H.; Kim, J.; Wulff, M.; Ihee, H.; Koch, M.H. Ultrafast X-ray solution scattering reveals different reaction pathways in the photolysis of triruthenium dodecacarbonyl (Ru3(CO)12) after ultraviolet and visible excitation. J. Am. Chem. Soc. 2010, 132, 2600–2607. [Google Scholar] [CrossRef] [PubMed]
- Biasin, E.; van Driel, T.B.; Kjær, K.S.; Dohn, A.O.; Christensen, M.; Harlang, T.; Vester, P.; Chabera, P.; Liu, Y.; Uhlig, J. Femtosecond X-Ray Scattering Study of Ultrafast Photoinduced Structural Dynamics in Solvated [Co(terpy)2]2+. Phys. Rev. Lett. 2016, 117, 013002. [Google Scholar] [CrossRef] [Green Version]
- Christensen, M.; Haldrup, K.; Bechgaard, K.; Feidenhans’l, R.; Kong, Q.; Cammarata, M.; Russo, M.L.; Wulff, M.; Harrit, N.; Nielsen, M.M. Time-Resolved X-ray Scattering of an Electronically Excited State in Solution. Structure of the 3A2u State of Tetrakis-μ-pyrophosphitodiplatinate(II). J. Am. Chem. Soc. 2009, 131, 502–508. [Google Scholar] [CrossRef]
- Kim, K.H.; Oang, K.Y.; Kim, J.; Lee, J.H.; Kim, Y.; Ihee, H. Direct observation of myoglobin structural dynamics from 100 picoseconds to 1 microsecond with picosecond X-ray solution scattering. Chem. Commun. 2011, 47, 289–291. [Google Scholar] [CrossRef]
- Kim, T.W.; Lee, J.H.; Choi, J.; Kim, K.H.; van Wilderen, L.J.; Guerin, L.; Kim, Y.; Jung, Y.O.; Yang, C.; Kim, J. Protein Structural Dynamics of Photoactive Yellow Protein in Solution Revealed by Pump–Probe X-ray Solution Scattering. J. Am. Chem. Soc. 2012, 134, 3145–3153. [Google Scholar] [CrossRef]
- Kim, J.G.; Kim, T.W.; Kim, J.; Ihee, H. Protein Structural Dynamics Revealed by Time-Resolved X-ray Solution Scattering. Acc. Chem. Res. 2015, 48, 2200–2208. [Google Scholar] [CrossRef]
- Yang, C.; Choi, M.; Kim, J.G.; Kim, H.; Muniyappan, S.; Nozawa, S.; Adachi, S.-i.; Henning, R.; Kosheleva, I.; Ihee, H. Protein Structural Dynamics of Wild-Type and Mutant Homodimeric Hemoglobin Studied by Time-Resolved X-Ray Solution Scattering. Int. J. Mol. Sci. 2018, 19, 3633. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Choi, M.; Kim, J.G.; Muniyappan, S.; Kim, H.; Kim, T.W.; Lee, Y.; Lee, S.J.; Kim, S.O.; Ihee, H. Effect of the abolition of intersubunit salt bridges on allosteric protein structural dynamics. Chem. Sci. 2021, 12, 8207–8217. [Google Scholar] [CrossRef] [PubMed]
- Cho, H.S.; Dashdorj, N.; Schotte, F.; Graber, T.; Henning, R.; Anfinrud, P. Protein structural dynamics in solution unveiled via 100-ps time-resolved x-ray scattering. Proc. Natl. Acad. Sci. USA 2010, 107, 7281–7286. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, S.J.; Kim, Y.; Kim, T.W.; Yang, C.; Thamilselvan, K.; Jeong, H.; Hyun, J.; Ihee, H. Reversible molecular motional switch based on circular photoactive protein oligomers exhibits unexpected photo-induced contraction. Cell. Rep. Phys. Sci 2021, 100512. [Google Scholar] [CrossRef]
- Kim, K.H.; Kim, J.G.; Oang, K.Y.; Kim, T.W.; Ki, H.; Jo, J.; Kim, J.; Sato, T.; Nozawa, S.; Adachi, S.-I. Femtosecond X-ray solution scattering reveals that bond formation mechanism of a gold trimer complex is independent of excitation wavelength. Struct. Dyn. 2016, 3, 043209. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Choi, E.H.; Kim, J.G.; Kim, J.; Ki, H.; Lee, Y.; Lee, S.; Yoon, K.; Kim, J.; Kim, J.; Ihee, H. Filming ultrafast roaming-mediated isomerization of bismuth triiodide in solution. Nat. Commun. 2021, 12, 4732. [Google Scholar] [CrossRef]
- Lee, Y.; Kim, J.G.; Lee, S.J.; Muniyappan, S.; Kim, T.W.; Ki, H.; Kim, H.; Jo, J.; Yun, S.R.; Lee, H. Ultrafast coherent motion and helix rearrangement of homodimeric hemoglobin visualized with femtosecond X-ray solution scattering. Nat. Commun. 2021, 12, 1–12. [Google Scholar] [CrossRef]
- Kim, J.G.; Nozawa, S.; Kim, H.; Choi, E.H.; Sato, T.; Kim, T.W.; Kim, K.H.; Ki, H.; Kim, J.; Choi, M. Mapping the emergence of molecular vibrations mediating bond formation. Nature 2020, 582, 520–524. [Google Scholar] [CrossRef]
- Kim, K.H.; Ki, H.; Lee, J.H.; Park, S.; Kong, Q.; Kim, J.; Kim, J.; Wulff, M.; Ihee, H. Solvent-dependent structure of molecular iodine probed by picosecond X-ray solution scattering. Phys. Chem. Chem. Phys. 2015, 17, 8633–8637. [Google Scholar] [CrossRef] [PubMed]
- Wulff, M.; Bratos, S.; Plech, A.; Vuilleumier, R.; Mirloup, F.; Lorenc, M.; Kong, Q.; Ihee, H. Recombination of photodissociated iodine: A time-resolved x-ray-diffraction study. J. Chem. Phys. 2006, 124, 034501. [Google Scholar] [CrossRef]
- Jun, S.; Lee, J.H.; Kim, J.; Kim, J.; Kim, K.H.; Kong, Q.; Kim, T.K.; Lo Russo, M.; Wulff, M.; Ihee, H. Photochemistry of HgBr2 in methanol investigated using time-resolved X-ray liquidography. Phys. Chem. Chem. Phys. 2010, 12, 11536–11547. [Google Scholar] [CrossRef]
- Kim, K.H.; Lee, J.H.; Kim, J.; Nozawa, S.; Sato, T.; Tomita, A.; Ichiyanagi, K.; Ki, H.; Kim, J.; Adachi, S.-i. Solvent-Dependent Molecular Structure of Ionic Species Directly Measured by Ultrafast X-Ray Solution Scattering. Phys. Rev. Lett. 2013, 110, 165505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dribinski, V.; Barbera, J.; Martin, J.P.; Svendsen, A.; Thompson, M.A.; Parson, R.; Lineberger, W.C. Time-resolved study of solvent-induced recombination in photodissociated IBr−(CO2)n clusters. J. Chem. Phys. 2006, 125, 133405. [Google Scholar] [CrossRef] [PubMed]
- Murov, S. Properties of Solvents Used in Organic Chemistry. Available online: http://murov.info/orgsolvents.htm#TABLE%202 (accessed on 2 September 2021).
- Lomont, J.P.; Shearer, A.J.; Nguyen, S.C.; Harris, C.B. Picosecond TRIR Studies of M3(CO)12 (M = Fe, Os) Clusters in Solution. Organometallics 2013, 32, 2178–2186. [Google Scholar] [CrossRef]
- Lampert, R.A.; Chewter, L.A.; Phillips, D.; O’Connor, D.V.; Roberts, A.J.; Meech, S.R. Standards for nanosecond fluorescence decay time measurements. Anal. Chem. 1983, 55, 68–73. [Google Scholar] [CrossRef]
- Dawson, W.R.; Windsor, M.W. Fluorescence yields of aromatic compounds. J. Phys. Chem. 1968, 72, 3251–3260. [Google Scholar] [CrossRef]
- Weigel, W.; Rettig, W.; Dekhtyar, M.; Modrakowski, C.; Beinhoff, M.; Schlüter, A.D. Dual Fluorescence of Phenyl and Biphenyl Substituted Pyrene Derivatives. J. Phys. Chem. A 2003, 107, 5941–5947. [Google Scholar] [CrossRef]
- Nozawa, S.; Adachi, S.I.; Takahashi, J.I.; Tazaki, R.; Guérin, L.; Daimon, M.; Tomita, A.; Sato, T.; Chollet, M.; Collet, E. Developing 100 ps-resolved X-ray structural analysis capabilities on beamline NW14A at the Photon Factory Advanced Ring. J. Synchrotron Rad. 2007, 14, 313–319. [Google Scholar] [CrossRef] [Green Version]
- Ichiyanagi, K.; Sato, T.; Nozawa, S.; Kim, K.-H.; Lee, J.-H.; Choi, J.; Tomita, A.; Ichikawa, H.; Adachi, S.; Ihee, H. 100 ps time-resolved solution scattering utilizing a wide-bandwidth X-ray beam from multilayer optics. J. Synchrotron Rad. 2009, 16, 391–394. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- James, F.; Roos, M. Minuit-a system for function minimization and analysis of the parameter errors and correlations. Comput. Phys. Commun. 1975, 10, 343–367. [Google Scholar] [CrossRef]
- Kim, J.; Kim, T.K.; Ihee, H. Density Functional and Spin− Orbit Ab Initio Study of CF3Br: Molecular Properties and Electronic Curve Crossing. J. Phys. Chem. A 2011, 115, 1264–1271. [Google Scholar] [CrossRef] [PubMed]
- Shao, Y.; Gan, Z.; Epifanovsky, E.; Gilbert, A.T.; Wormit, M.; Kussmann, J.; Lange, A.W.; Behn, A.; Deng, J.; Feng, X. Advances in molecular quantum chemistry contained in the Q-Chem 4 program package. Mol. Phys. 2015, 113, 184–215. [Google Scholar] [CrossRef] [Green Version]
- Barone, V.; Cossi, M. Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]
- Cossi, M.; Rega, N.; Scalmani, G.; Barone, V. Energies, structures, and electronic properties of molecules in solution with the C-PCM solvation model. J. Comput. Chem. 2003, 24, 669–681. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef] [Green Version]
- Beck, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys 1993, 98, 5648. [Google Scholar] [CrossRef] [Green Version]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [Green Version]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Staroverov, V.N.; Scuseria, G.E.; Tao, J.; Perdew, J.P. Comparative assessment of a new nonempirical density functional: Molecules and hydrogen-bonded complexes. J. Chem. Phys. 2003, 119, 12129–12137. [Google Scholar] [CrossRef]
- Pritchard, B.P.; Altarawy, D.; Didier, B.; Gibson, T.D.; Windus, T.L. New Basis Set Exchange: An Open, Up-to-Date Resource for the Molecular Sciences Community. J. Chem. Inf. Model. 2019, 59, 4814–4820. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, I.; Geering, H.; Rose, M.; Crossan, A. A simple method to estimate entropy and free energy of atmospheric gases from their action. Entropy 2019, 21, 454. [Google Scholar] [CrossRef] [PubMed] [Green Version]






| Cyclohexane | Methanol | |
|---|---|---|
| Fraction of photoexcited molecules 1 | 20.0 (± 1.1)% | - |
| Fraction of direct, nonradiative relaxation back to the ground state 2 | 14.8 (± 0.9)% | - |
| Fraction of C2F4I· dissociating to C2F4 + I· | 30 (± 1.1)% | 20 (± 1.3)% |
| C2F4I· → C2F4 + I· | 3.4 (± 2.9) × 109 s–1 | 3.3 (± 2.1) × 109 s–1 |
| I· + I· → I2 | 1.1 (± 0.8) × 1010 M–1s–1 | 4.4 (± 1.3) × 1010 M–1s–1 |
| Species | Structural Parameters 1 | Optimized Values 2 | ωB97X/def2-TZVPP | M06-2X/def2-TZVPP | B3LYP-D3/def2-TZVPP |
|---|---|---|---|---|---|
| anti-C2F4I2 | r(C−I) | 2.145 (± 0.03) Å | 2.137 Å | 2.147 Å | 2.203 Å |
| ∠C−C−I | 112.4 (± 9.8)° | 111.7° | 111.1° | 111.4° | |
| gauche-C2F4I2 | r(C−I) | 2.140 (± 0.05) Å | 2.137 Å | 2.138 Å | 2.188 Å |
| ∠C−C−I | 115.6 (± 10.4)° | 113.5° | 113.5° | 114.0° | |
| anti-C2F4I· | r(C−I) | 2.156 (± 0.04) Å | 2.163 Å | 2.176 Å | 2.248 Å |
| ∠C−C−I | 119.2 (± 8.2)° | 111.8° | 111.8° | 112.2° | |
| gauche-C2F4I· | r(C−I) | 2.138 (± 0.05) Å | 2.129 Å | 2.137 Å | 2.191 Å |
| ∠C−C−I | 118.1 (± 9.4)° | 111.0° | 111.0° | 110.1° | |
| I2 | r(I−I) | 2.661(± 0.08) Å | 2.657 Å | 2.653 Å | 2.702 Å |
| ωB97X | M06-2X | B3LYP-D3 | PBE0 | TPSSh | |
|---|---|---|---|---|---|
| def2-TZVPP | 0.007 Å | 0.010 Å | 0.065 Å | 0.032 Å | 0.036 Å |
| 4.4° | 4.4° | 4.5° | 5.8° | 5.8° | |
| cc-pVTZ(-PP) 1 | 0.009 Å | 0.014 Å | 0.075 Å | 0.069 Å | 0.045 Å |
| 4.5° | 4.5° | 4.7° | 5.7° | 5.6° | |
| aug-cc-pVTZ(-PP) 2 | 0.007 Å | 0.013 Å | 0.071 Å | 0.038 Å | 0.041 Å |
| 4.4° | 4.4° | 4.5° | 5.6° | 5.6° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, J.; Lee, S.; Eom, S.; Ki, H.; Choi, E.H.; Lee, Y.; Nozawa, S.; Adachi, S.-i.; Kim, J.; Ihee, H. Structural Dynamics of C2F4I2 in Cyclohexane Studied via Time-Resolved X-ray Liquidography. Int. J. Mol. Sci. 2021, 22, 9793. https://doi.org/10.3390/ijms22189793
Gu J, Lee S, Eom S, Ki H, Choi EH, Lee Y, Nozawa S, Adachi S-i, Kim J, Ihee H. Structural Dynamics of C2F4I2 in Cyclohexane Studied via Time-Resolved X-ray Liquidography. International Journal of Molecular Sciences. 2021; 22(18):9793. https://doi.org/10.3390/ijms22189793
Chicago/Turabian StyleGu, Jain, Seonggon Lee, Seunghwan Eom, Hosung Ki, Eun Hyuk Choi, Yunbeom Lee, Shunsuke Nozawa, Shin-ichi Adachi, Jeongho Kim, and Hyotcherl Ihee. 2021. "Structural Dynamics of C2F4I2 in Cyclohexane Studied via Time-Resolved X-ray Liquidography" International Journal of Molecular Sciences 22, no. 18: 9793. https://doi.org/10.3390/ijms22189793
APA StyleGu, J., Lee, S., Eom, S., Ki, H., Choi, E. H., Lee, Y., Nozawa, S., Adachi, S. -i., Kim, J., & Ihee, H. (2021). Structural Dynamics of C2F4I2 in Cyclohexane Studied via Time-Resolved X-ray Liquidography. International Journal of Molecular Sciences, 22(18), 9793. https://doi.org/10.3390/ijms22189793