Next Article in Journal
The Cytokine Growth Differentiation Factor-15 and Skeletal Muscle Health: Portrait of an Emerging Widely Applicable Disease Biomarker
Next Article in Special Issue
Self-Diffusion in Confined Water: A Comparison between the Dynamics of Supercooled Water in Hydrophobic Carbon Nanotubes and Hydrophilic Porous Silica
Previous Article in Journal
Effect of Ni Substitution on the Structural, Magnetic, and Electronic Structure Properties of Gd0.4Tb0.6(Co1−xNix)2 Compounds
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
IJMS
Volume 23
Issue 21
10.3390/ijms232113178
ijms-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Four-Component Relativistic Calculations of NMR Shielding Constants of the Transition Metal Complexes—Part 2: Nitrogen-Coordinated Complexes of Cobalt

by
Dmitry O. Samultsev
,
Valentin A. Semenov
,
Irina L. Rusakova
and
Leonid B. Krivdin
*
A. E. Favorsky Irkutsk Institute of Chemistry, Siberian Branch of the Russian Academy of Sciences, Favorsky St. 1, Irkutsk 664033, Russia
*
Author to whom correspondence should be addressed.
Int. J. Mol. Sci. 2022, 23(21), 13178; https://doi.org/10.3390/ijms232113178
Submission received: 12 October 2022 / Revised: 26 October 2022 / Accepted: 26 October 2022 / Published: 29 October 2022
(This article belongs to the Special Issue Modern NMR Characterization of Materials)
Browse Figures
Versions Notes

Abstract

:
Both four-component relativistic and nonrelativistic computations within the GIAO-DFT(PBE0) formalism have been carried out for 15N and 59Co NMR shielding constants and chemical shifts of a number of the nitrogen-coordinated complexes of cobalt. It was found that the total values of the calculated nitrogen chemical shifts of considered cobalt complexes span over a range of more than 580 ppm, varying from −452 to +136 ppm. At that, the relativistic corrections to nitrogen shielding constants and chemical shifts were demonstrated to be substantial, changing accordingly from ca. −19 to +74 ppm and from −68 to +25 ppm. Solvent effects on 15N shielding constants and chemical shifts were shown to have contributions no less important than the relativistic effects, namely from −35 to +63 ppm and from −74 to +23 ppm, respectively. Cobalt shielding constants and chemical shifts were found to vary in the ranges of, accordingly, −20,157 to −11,373 ppm and from +3781 to +13,811. The relativistic effects are of major importance in the cobalt shielding constants, resulting in about 4% for the shielding-type contributions, while solvent corrections to cobalt shielding constants appeared to be of less significance, providing corrections of about 1.4% to the gas phase values.

Graphical Abstract

1. Introduction

Noble metal complexes have become of primary importance in many areas of modern chemistry; however, the high cost of noble metals essentially hinders their large-scale application and industrialization. In this respect, extensive attention has been paid to the non-noble metal complexes, such as those of cobalt, rhodium, ruthenium, and iridium, providing the most interest and perspective. In particular, cobalt complexes are extensively studied nowadays as potentially important synthetic products capable of exhibiting antiulcer and anti-microbial activities [1,2,3,4,5,6]. The present study deals with cobalt ionic complexes with nitrogen-donor ligands that represent a potential interest in biochemistry.
Nitrogen and cobalt NMR spectroscopy makes up an efficient tool for the structural elucidation of cobalt ammine complexes. Chemical shifts of both NMR-active nitrogen isotopes, 14N (S = 1) and 15N (S = 1/2), span over the range of about 900 ppm [7]. The 59Co isotope has 100% natural abundance and its chemical shift range is extremely wide, being about 20,000 ppm [8], which is the largest among the known NMR scales. In this regard, accurate theoretical predictions of the NMR chemical shifts provide a powerful tool for the structural elucidation of organic and bioorganic molecules, transition metal complexes, and related species [9,10,11,12,13]. In this respect, NMR chemical shifts, nitrogen and cobalt in particular, represent an undoubted challenge [14,15,16,17,18]. Moreover, cobalt complexes are computationally demanding on their own, as they possess intricate electronic structures characterized, in particular, by the energetically low-lying transitions [19], which assume an important role in electron correlation effects.
This work represents an important part of our study on the computational aspects of the NMR shielding constants of the transition metal complexes. The primary concern of the present study was to estimate the 15N NMR chemical shifts (CSs) in a large variety of nitrogen-coordinated cobalt complexes within the framework of density functional theory (DFT) [20]. To the best of our knowledge, despite a good deal of experimental information on the nitrogen chemical shifts of cobalt ammine complexes reported so far [21,22,23,24], the corresponding computational results are practically absent.
In our previous paper [25], the first attempt to estimate the 15N NMR chemical shifts of three pentaamine aqua complexes of cobalt(III), rhodium(III), and iridium(III) at the nonrelativistic and four-component relativistic DFT-PBE0 [26,27] levels of theory has been made. The relativistic results appeared to be very close to the experiment. That is why we adopted many aspects of the presented computational protocol in the present study. Moreover, in that work, we found noticeable relativistic corrections to the nitrogen shielding constants (of up to 20 ppm) in the cobalt pentaamine complex as a result of the manifestation of the so-called relativistic “Heavy Atom on Light Atom” (HALA) effect, originally described by Nomura and Takeuchi [28]. In the present paper, we consider relativistic corrections to nitrogen chemical shifts in a large number of nitrogen-coordinated cobalt complexes with different ligands and investigate the role of the HALA effect in more detail. Another part of the present study deals with the calculation of cobalt shielding constants (SCs) in the nitrogen-coordinated cobalt complexes within the same DFT-based methodology. In our previous paper [25], we evaluated the cobalt shielding constant in the [Co(NH3)5H2O]3+ complex at the four-component DFT-PBE0 level to be approximately −18,236 ppm, while relativistic correction was found to be 892 ppm, which is 4.8% of the total relativistic value.
Since the mid-1990s, transition metal chemical shifts [29,30] have routinely been calculated at the DFT level, including 59Co NMR chemical shifts as the prime goal of such computations [19,31,32,33,34,35,36,37]. The first attempts to calculate 59Co NMR chemical shifts using the density functional approach were made by Chan et al. [19]. They calculated 59Co chemical shifts and chemical shift anisotropies of several hexacoordinated Co(III) complexes using the sum-over-states density functional perturbation theoretical method using individual gauges localized orbitally (SOS-DFPT-IGLO) [38,39]. From the solid-state NMR data presented in their paper, it followed that they underestimated the isotropic chemical shifts of 59Co approximately by two times as compared to the experiment. Later, Chan et al. [31,32] continued the study of the computational protocol for the 59Co chemical shifts in hexacoordinated cobalt(III) complexes and, as a result, it was found that hybrid DFT exchange-correlation (XC) functionals were more suitable for the 59Co shielding calculations, as compared to the pure XC functionals. It was also found that the gauge-including atomic orbitals (GIAO) [40,41,42] scheme provided cobalt CSs of a better agreement with the experimental values than the IGLO [38,39] scheme did.
Godbout et al. [33] performed the density functional calculations of the isotropic 59Co NMR CSs of some anionic, cationic, and neutral Co(III) complexes using a hybrid XC B3LYP functional [43,44] within the GIAO formalism. Those results appeared to be of average quality, deviating from the experimental data by no more than 2000 ppm for the cobalt shift scale, covering the range of 20,000 ppm. Overall, Godbout et al., reached several important conclusions, namely that (i) f-type functions do not appear to be essential for the correct description of a cobalt atom in the calculations of its shielding constant at the DFT level; (ii) the relativistic effects are not important in this case, so there is no need to apply the relativistic level of theory; (iii) there are no systematic differences between shielding constants calculated for anionic and cationic complexes, so the charge field effects are small.
The hybrid density functional theoretical study of 59Co NMR chemical shifts and shift tensor components in the hexacoordinated Co(III) porphyrin system has been carried out by Xu and Au-Yeung [34]. They applied the B3LYP/6-311G ** level of theory using experimental geometry and obtained an excellent agreement with the solid-state NMR experimental data. It was found that the diamagnetic shielding of 59Co is close to that of the free atom value of 2166 ppm calculated by Malli [45] and that agreement between the HF method and experimental results is very poor, confirming the fact that electron correlation effects play an essential role in cobalt shielding calculations.
Advanced computations of cobalt chemical shifts that covered the range of about 20,000 ppm have been carried out by Grigoleit et al. [35] for the representative series of electron-rich organometallic and high-valent inorganic Co(III) complexes. In that study, the GIAO-DFT-B3LYP approach had been used in both static calculations on the equilibrium geometries as well as in combination with the methods that include zero-point and classical thermal effects. Mean absolute deviations between averaged and experimental δ(59Co) values reported in Ref. [35] appeared to be of the order of 500–760 ppm over a chemical shift range of almost 20,000 ppm. The authors had come to a very important conclusion about the vibrational and solvent effects on 59Co NMR chemical shifts, namely that taking into account the zero-point and thermal averaging effects results in the insignificant deshielding of 59Co nuclei. At that, the largest errors originate in the solvation effects, which are to be addressed by means of employing the highest feasible level of theory by implying an appropriate solvation model.
Density functional calculations of 59Co NMR chemical shifts using the zeroth-order regular approximation (ZORA) [46] were reported in [36,37]. Thus, Ooms and co-authors [36] presented an experimental solid-state 13C and 59Co NMR study of five octahedral Co(III) cations, corroborated by ZORA-DFT calculations, which were carried out without taking into account solvent or vibrational corrections. Indeed, calculated CSs agreed well with the experimental values; however, a significant deviation of more than 2300 ppm for [Co(CH3)(en)2(N3)]+ (en = ethylenediamine) was found. In another paper by Senn et al. [37], the ligand-field density functional theory (LF-DFT) approach was employed for the calculations of 59Co NMR shielding tensor of all four diastereoisomers of tris(1,2-ethanediamine) cobalt(III) complex ion, [Co(en)3]3+. Those results were compared with the conventional ZORA-DFT calculations and with corresponding experimental values. It was found that the LF-DFT approach slightly overestimated (by several hundreds of ppm) while ZORA-DFT slightly underestimated the experimental values.
In this paper, we shall employ a full four-component GIAO-DFT approach with hybrid functional PBE0 to calculate 59Co NMR chemical shifts in a wide series of nitrogen-coordinated cobalt complexes and to pinpoint the typical magnitudes of relativistic effects for cobalt shielding constants and chemical shifts. Predicted cobalt chemical shifts will allow one to determine a range of informative 59Co NMR spectra for the related nitrogen-coordinated cobalt complexes.

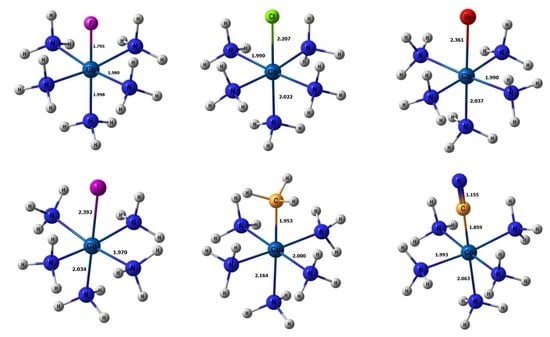
2. Results and Discussion

Stereochemical structures, together with calculated geometric parameters of complexes 1–27 optimized at the DFT-PBE0/ATZP level, are shown in Figure 1. The corresponding calculated 15N shielding constants (σtot), together with theoretical (δtot) and experimental chemical shifts (δexp), are given in Table 1.
In Table 1, σGP, Δsolv, Δrel, and σtot stand, respectively, for the gas phase values of nitrogen shielding constants, solvent corrections to nitrogen SCs, relativistic corrections to nitrogen SCs, and total values of nitrogen SCs, while δtot and δexp are the total theoretical and experimental nitrogen chemical shifts. Basic gas phase values were calculated at the DFT-PBE0 level of theory using relativistic Dyall’s core-valence basis set of triple zeta quality, dyall.cv3z [47,48], on cobalt atoms, aug-pcS-2 [49] on nitrogen atoms, aug-cc-pVDZ [50,51] on oxygen atoms, pc-2 [52,53] on carbon atoms, and pc-1 [52,53] on hydrogens. For the sake of convenience, the mentioned basis set scheme will be referred to as BaS. In all calculations of shielding constants, we have used GIAO formalism to treat the gauge origin problem [13,54].
Used in our calculations, the hybrid PBE0 functional represents the combination of the PBE generalized gradient functional [55], in which all parameters (except those related to the local spin density) are fundamental constants, with a 25% admixture of the Hartree−Fock (HF) exchange.
Solvent corrections to the 15N SCs were estimated as the differences between the SC values obtained at the DFT-PBE0/BaS level within the polarizable continuum model using the integral equation formalism (IEF-PCM) [56,57], specified for the H2O solvent, and the GP values, evaluated at the same level of theory.
Relativistic corrections to the 15N SCs were evaluated within the GIAO-DFT-PBE0 method as the differences between the four-component relativistic values and the approximated nonrelativistic values. In all the four-component calculations, we generated the small-component basis space by applying the unrestricted kinetic balance (UKB) [58] to the large-component basis set. This was done in order to approximate the magnetic kinetic balance (MKB) condition [59], because, as was found by Olejniczak et al. [60], the GIAOs make MKB an atomic one [61]. As a result, it becomes possible to obtain the magnetic balance by extending the orbitals, retrieved from a self-consistent field (SCF) calculation with the restricted kinetic balance (RKB) condition [58] by extending with their UKB complement. In both relativistic and approximated nonrelativistic four-component calculations, we have used the same basis set scheme, BaS, as in the nonrelativistic calculations. The only difference is that all basis sets were taken in an uncontracted form, BaS(un). This is due to the poor suitability of the nonrelativistic contraction schemes for the four-component relativistic calculations [62].
In order to obtain the correct nonrelativistic limit, we have investigated the convergence of the nitrogen shielding constant in [Co(NH3)6]3+ with the increasing of the speed of light value (c ~ 137.036 a.u.) by several times, namely starting from 700 a.u. (~5c) to 2000 a.u. (~14c) in the four-component GIAO-DFT-PBE0 calculations. The corresponding graph is presented in Figure 2. In that way, the values at 1800–2000 a.u. can solidly be regarded as the converged ones. Thus, we have chosen c = 1800 a.u. (we will call it the “13c scheme”) to calculate the approximated nonrelativistic values of nitrogen shielding constants.
The total values of nitrogen SCs in Table 1 represent the sum of σGP, Δsolv, and Δrel:
σtot = σGP + Δsolv + Δrel
The total values of nitrogen chemical shifts δtot in Table 1 were calculated using the linear regression analysis [63,64,65]. The strategy of this approach consists of the mapping of the observed chemical shifts onto the predicted shielding constants, in which the relationship is simulated by the linear model:
σ = Aδ + B
The coefficient A represents a slope (the tangent of the line angle) and B is the intercept of the model with the σ-axis (which corresponds to the approximated shielding constant of the reference compound). In the absence of systematic errors, coefficient A takes the value of −1, while B becomes σref. In the present case, total nitrogen SCs (σtot) were mapped to available experimental CSs (δexp), and the parameters of the linear regression model were obtained as A = −1.1045 and B = −179.90. The correlation plot of the final calculated 15N NMR chemical shifts (δtot) versus corresponding experimental values (δexp) is shown in Figure 3. In general, given that total CSs span the range from −451.6 to +136.1 ppm (a range of more than 580 ppm), the agreement of the calculated nitrogen CSs with the experiment is rather good: the correlation coefficient is 0.901, the corrected mean absolute error (CMAE) is 6.5 ppm, and the mean absolute percentage error (MAPE) is only 1.14%.
As can be seen in Table 1, the relativistic corrections to nitrogen shielding constants can be substantial, varying from −19 ppm in [Co(NH3)5CN]2+ (cis-orientation) to 74 ppm in cis,mer-[Co(NH3)2(NO2)3CH3]− (trans-orientation to NO2), see Figure 4. In an absolute value, the relativistic corrections to the nitrogen SCs can reach up to 37% of the relativistic SCs. Apparently, large relativistic corrections to nitrogen shielding constants are due to the well-known SO-HALA effect [66] on nitrogen shieldings initiated by the neighboring cobalt atom.
The mechanism of the SO-HALA effect consists of the interaction of the spin-orbit coupling (SOC) at the heavy atom with the magnetic dipole at the light nucleus. Namely, in the presence of an external magnetic field, SOC produces additional electronic spin polarization, which propagates to the light nucleus and changes the magnetic field at the light nucleus via the FC interaction [67,68]. Due to its nonlocal character, the sign and magnitude of the SO-HALA effect can give information about the electronic structure of the heavy atom and its surroundings [69,70,71,72]. In particular, it reflects the coordination environment of the heavy atom center [73] and gives information on the polar/covalent character of the heavy–light atom bond [72,74]. Moreover, from the sign of the SO-HALA effect, one can deduce the character of the frontier orbitals participating in the SO-HALA mechanism. Namely, the deshielding SO-HALA effect is associated with the occupied σ-type heavy–light atom bonding molecular orbitals, while the π-type orbitals provide a shielding-type SO-HALA effect [68,75]. These findings were confirmed for hydrogen and carbon shielding constants by Kaupp et al. [76,77,78,79], Bagno et al. [80], and Ruiz-Morales et al. [81], who carried out the full four-component DFT investigations of the SO-HALA effects in the transition-metal complexes involving molecular orbital analysis.
Based on our results, it follows that the magnitude and sign of this effect are dependent on the electronic nature of ligands. Apparently, this can be explained by the concept discussed above. Indeed, the sign of the SO-HALA effect observed in the series of cobalt complexes 1–27 is likely defined by the interplay of the involvement of the occupied σ- and π-type metal d-orbitals in the bonding metal orbital with the NMR spectator nitrogen atom, which should be influenced by the electronic nature of the ligands sharing the same cobalt–nitrogen bonding orbital. The positive sign of most of the relativistic corrections to nitrogen SCs in compounds 1–27 is due to the fact that the negative paramagnetic contributions decrease in their absolute values when going to the relativistic consideration, while diamagnetic terms stay practically unchanged. This indicates that the observed SO-HALA effect provides shielding-type contributions to the paramagnetic terms, resulting in their increase if one takes into account their negative sign. Based on these observations, the occupied π-type metal d-orbitals play a predominant role in the observed SO-HALA effect on the nitrogen SCs in most of the considered cobalt complexes 1–27. Otherwise, the SO-HALA effect is probably governed by the σ-type occupied metal d-orbitals.
Based on the simplified IUPAC formula for chemical shift [82,83], we have also estimated the relativistic corrections to nitrogen chemical shifts as the differences between the relativistic correction to nitrogen shielding constant in nitrogen reference compound (nitromethane, CH3NO2) and those in cobalt complexes 1–27:
Δrelδ = Δrelσref − Δrelσ
According to the present results, relativistic correction to the nitrogen SC in CH3NO2 is only 5.3 ppm. Subtracting the relativistic corrections to nitrogen SCs in compounds 1–27 from this value (5.3 ppm) gives relativistic corrections to the nitrogen CSs of ca. −68 to +25 ppm.
An important conclusion that can be arrived at from these figures is that the relativistic SO-HALA corrections to the nitrogen chemical shifts in the vast majority of cases are negative (i.e., of the shielding type), shifting nitrogen signals to a higher field. The magnitude of the SO-HALA effect on nitrogen is dependent on the nature of ligands and sometimes it can be rather substantial, so we recommend applying the relativistic level of theory when calculating nitrogen CSs in the nitrogen-coordinated complexes of cobalt.
Additionally, we have evaluated solvent corrections to the nitrogen SCs and CSs; see Table 1 and Figure 5. Solvent corrections to SCs were found to be of −34.6 to +63.2 ppm in this series. Based on the solvent correction to nitrogen SC in nitromethane of −11.2 ppm (Δsolvσref), we estimated the solvent corrections to nitrogen CSs in the whole series of 1–27 as:
Δsolvδ = Δsolvσref − Δsolvσ
Solvent corrections to nitrogen CSs were found to be in the range of −74.4 to +23.4 ppm. In view of the significance of solvent corrections to nitrogen CSs, we suggest taking them into account when calculating nitrogen CSs in the nitrogen-coordinated complexes of cobalt.
Additionally, we have calculated 59Co NMR shielding constants and chemical shifts within the same computational protocol as was used for nitrogen. However, in view of the lack of experimental data for cobalt NMR, we did not apply the linear regression analysis for cobalt chemical shifts. Instead, we used the approximated IUPAC formula [82,83]:
δtot = σtot(ref) − σtot,
where σtot(ref) is the total value of cobalt SC of the reference [Co(CN)6]3−, and σtot is the total cobalt SC of the given compound. These results are presented in Table 2.
To calculate the correct nonrelativistic values of σ (which are needed for the evaluation of Δrelσ), we have studied the convergence of the cobalt σ value in the hexacyanocobaltate (III) anion [Co(CN)6]3− with the increasing of the speed of light, in the same way as was done for the nitrogen SC. The corresponding graph is presented in Figure 6.
As can be seen in Figure 6, the calculated σ varies insignificantly (within 1 ppm) starting from 1800 a.u. To calculate the nonrelativistic limit for the cobalt shielding, we have also chosen the “13c scheme”.
As follows from Table 2, the total calculated SCs of cobalt (σtot) are negative, varying from −20,157 to −11,373 ppm, depending on ligands. The relativistic effects were found to play a significant role for 59Co SCs, providing, on average, a shielding-type contribution of about 4% in the range of 2–10% of the total values; see Figure 7.
At that, the total cobalt CSs (δtot) span over the range from 3781 to 13811 ppm. Given such a wide range of cobalt CSs, it is interesting to compare calculated values with the experimental data whenever it is possible. Having no experimental data for the whole series of considered compounds, we can at least make a comparison for a couple of cobalt complexes; namely, for cis-[Co(NH3)4CO3]+ (13) and [Co(NH3)6]3+ (25). According to the solid-state NMR data, the cobalt chemical shifts of compounds 13 and 25 referenced to [Co(CN6)]3− are 9691 ppm [33] (9700 ppm [19]) and 8153 ppm [33] (8176 ppm [35]), respectively. Our total calculated values for these compounds are, accordingly, 9194.0 and 9223.1 ppm. Hence, the discrepancy between our theoretical values and the solid-state NMR experimental values for compounds 13 and 25 is about 500 (5% to δtot) and 1000 ppm (11% to δtot), respectively. Based on the analysis of previous calculations of 59Co NMR CSs [19,33,35,36], we have achieved rather good accuracy for the calculated cobalt chemical shifts in this paper.
The relativistic corrections can be estimated as 2–14% with an average relative value of about 5%, which is far from being negligible. In that way, we do not agree with Godbout and Oldfield [33] that taking into account relativistic effects when calculating cobalt chemical shifts is not essential to reproduce the experimental data. On the contrary, the relativistic level of theory is essentially important, because relativistic corrections to 59Co NMR chemical shifts of cobalt complexes may be of minor significance in some compounds, but can reach up to 14% of the total value for other complexes. The magnitude of the relativistic effects is determined by the electronic structure of a compound under consideration, and it is difficult to say a priori whether it is appropriate to neglect the relativistic corrections.
Solvent effects in the 59Co shielding constants appeared to be less important than the relativistic ones, giving an overall contribution of about 0.1–3.2% to the gas phase values; see Figure 8.

3. Materials and Methods

The geometry optimization of the nitrogen-coordinated complexes of cobalt 1–27 was performed at the DFT-PBE0/ATZP level using the GAUSSIAN 09 code [84]. As was shown earlier [85], the contribution of relativistic geometry to the resulting 15N NMR shielding constants was insignificant and could safely be ignored. Therefore, in the present study, the optimization of the geometric parameters of the studied complexes was carried out at the non-relativistic level of theory. The corresponding Cartesian coordinates of all studied compounds are given in the Supplementary Materials.
All four- and one-component calculations of the 15N and 59Co NMR shielding constants were performed with the GIAO-DFT-PBE0 method within the Dirac 2016 [86] and Gaussian 09 [84] programs. We have used the DFT formalism at all levels due to the fact that it represented the most suitable tool for our study. Indeed, it takes into account the electron correlation effects via the XC potential and scales as O(n4) [87] at the same time. Despite some disadvantages connected with its inability to systematically improve the accuracy of the results [88] and some issues of triplet instability problems [89], the DFT approach is capable of providing high-quality results, which are comparable to those obtained within the modern ab initio correlated wavefunction-based methods [90].
Therefore, the DFT formalism provides an alternative avenue for the rigorous quantum mechanical calculations of the NMR properties of larger molecular systems, which are beyond the reach and scope of the ab initio correlated wavefunction-based methods. That is why DFT has become very popular in the calculations of the NMR parameters of transition metal complexes (see introduction), and we decided not to digress from a well-proven computational method. Moreover, it is worth noting that, for today, the density functional approach is the only available means of simultaneous taking into account electron correlation and relativistic effects when applied under a relativistic framework.
In all calculations of shielding constants, we used the PBE0 XC functional. This functional indeed provides very accurate results for NMR chemical shifts. In particular, a computational study of the performances of the PBE and PBE0 functionals in application to the shielding constants of light NMR nuclei of the first and second periods was carried out by Adamo and Barone [91]. In that study, they chose quite a large reference set, which included molecules with different hybridizations and chemical environments of the nuclei of interest. It was demonstrated that the PBE0 protocol appeared to be competitive with the low-order perturbation post-HF techniques (such as MP2) for the “well-behaved” systems and provided significantly improved results in the presence of strong correlation effects.
As a result, we carried out geometry optimizations of all nitrogen-coordinated complexes of cobalt using this functional. This was done in line with the recent findings by Giovanetti et al. [92], who studied the effects of the geometry on fluorine spin–spin coupling constants and reached the conclusion that geometry optimization at the same level of theory as that used for the calculation of spin–spin coupling constants generally improves the quality of the final results.
We suppose that this observation can be explained as follows: using the same particular functional in both the geometry optimization and calculation of any triplet property provides the most stable results in the sense of the triplet instability problem [89]. In the present case, we deal with relativistic corrections, which can be expressed as multiple response functions of different orders depending, in particular, on the matrix elements of hyperfine triplet operators of different types [93,94]. Thus, guided by this reasoning, we decided not to introduce any additional factors that can disturb the stability of all relativistic DFT calculations and used the same XC functional in both equilibrium geometry and shielding constant calculations.

4. Conclusions

Both four-component relativistic and nonrelativistic computations within the GIAO-DFT(PBE0) formalism were carried out for 15N and 59Co NMR shielding constants and chemical shifts of a number of the nitrogen-coordinated complexes of cobalt. It was found that the total values of the calculated nitrogen chemical shifts of the cobalt complexes span over the range of more than 580 ppm, varying from −452 to +136 ppm. At that, the relativistic corrections to nitrogen shielding constants and chemical shifts were found to be substantial, varying from −19 to +74 ppm and from −68 to +25 ppm, respectively. The positive sign of the most part of the relativistic corrections to nitrogen SCs was found to be due to the fact that the negative paramagnetic contributions decrease in their absolute values when referring to the relativistic consideration, while diamagnetic terms stay practically unchanged. This indicates that the observed relativistic SO-HALA effect initiated by cobalt gives the shielding-type contributions, resulting in the increasing and decreasing of the nitrogen SCs and CSs, respectively, shifting the latter to a higher field. In this sense, we recommend not neglecting the relativistic level of theory when calculating the nitrogen CSs in the nitrogen-coordinated complexes of cobalt. Solvent corrections to nitrogen SCs and CSs were shown to vary from −34.6 to +63.2 ppm and from −74.4 to +23.4 ppm, accordingly. Cobalt SCs (−20,157 to −11,373 ppm) and CSs (+3781 to +13,811 ppm) were found to be essentially large. The relativistic effects were demonstrated to play a significant role for cobalt SCs, resulting in shielding-type contributions of 4% on average, while solvent corrections to the cobalt SCs appeared to be less significant, affecting the gas phase values by 1.4% on average.

Supplementary Materials

The following supporting information can be downloaded at: www.mdpi.com/article/10.3390/ijms232113178/s1.

Author Contributions

Conceptualization, supervision: L.B.K.; writing—original draft preparation, writing—review and editing, methodology: I.L.R.; validation, formal analysis, investigation, data curation, visualization, funding acquisition: D.O.S. and V.A.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Russian Science Foundation, grant number 21-73-00182.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The calculations were performed at Irkutsk Supercomputer Center of the Siberian Branch of the Russian Academy of Sciences using the HPC cluster “Academician V.M. Matrosov” (http://hpc.icc.ru, accessed on 1 October 2022) and at A.E. Favorsky Irkutsk Institute of Chemistry using the facilities of Baikal Analytical Center (http://ckp-rf.ru/ckp/3050, accessed on 1 October 2022).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Yeşilela, O.Z.; Mutlu, A.; Darcan, C.; Büyükgüngör, O. Syntheses, structural characterization and antimicrobial activities of novel cobalt-pyrazine-2,3-dicarboxylate complexes with N-donor ligands. J. Mol. Struct. 2010, 964, 39–46. [Google Scholar] [CrossRef]
  2. Mishra, A.; Kaushik, N.K.; Verma, A.K.; Gupta, R. Synthesis, characterization and antibacterial activity of cobalt(III) complexes with pyridine–amide ligands. Eur. J. Med. Chem. 2008, 43, 2189–2196. [Google Scholar] [CrossRef] [PubMed]
  3. Shalash, A.M.; Abu Ali, H.I. Synthesis, crystallographic, spectroscopic studies and biological activity of new cobalt(II) complexes with bioactive mixed sulindac and nitrogen-donor ligands. Chem. Cent. J. 2017, 11, 40. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  4. Miodragović, D.U.; Bogdanović, G.A.; Miodragović, Z.M.; Radulović, M.D.; Novaković, S.B.; Kaluderović, G.N.; Kozłowski, H. Interesting coordination abilities of antiulcer drug famotidine and antimicrobial activity of drug and its cobalt(III) complex. J. Inorg. Biochem. 2006, 100, 1568–1574. [Google Scholar] [CrossRef] [PubMed]
  5. Fang, W.-Y.; Xu, M.; Zhu, C.-G.; Wei, Y.-J.; Wang, F.-W. Synthesis, Structures, and Antimicrobial Studies of Cobalt(III) Complexes with Tridentate Schiff Bases. Synth. React. Inorg. Met.-Org. Nano-Met. Chem. 2012, 42, 109–114. [Google Scholar] [CrossRef]
  6. Dorkova, P.; Pantcheva, I.N.; Sheldrick, W.S.; Mayer-Figge, H.; Petrova, R.; Mitewa, M. Synthesis, structure and antimicrobial activity of manganese(II) and cobalt(II) complexes of the polyether ionophore antibiotic Sodium Monensin A. J. Inorg. Biochem. 2008, 102, 26–32. [Google Scholar] [CrossRef]
  7. Witanowski, M.; Webb, G.A. Nitrogen NMR, 1st ed.; Plenum Press: New York, NY, USA, 1973. [Google Scholar] [CrossRef]
  8. Chan, J.C.C.; Au-Yeung, S.C.F. Cobalt-59 NMR spectroscopy. Ann. Rep. NMR Spectrosc. 2000, 41, 1–54. [Google Scholar] [CrossRef]
  9. Jensen, F. Introduction to Computational Chemistry; John Wiley and Sons Ltd.: Chichester, UK, 2007; p. 624. [Google Scholar]
  10. Sauer, S.P.A. Molecular Electromagnetism: A Computational Chemistry Approach; University Press: Oxford, UK, 2012; p. 322. [Google Scholar]
  11. Krivdin, L.B. Computational 1H and 13C NMR in structural and stereochemical studies. Magn. Reson. Chem. 2022, 60, 733–828. [Google Scholar] [CrossRef]
  12. Rusakova, I.L.; Rusakov, Y.Y. Quantum chemical calculations of 77Se and 125Te nuclear magnetic resonance spectral parameters and their structural applications. Magn. Reson. Chem. 2021, 59, 359–407. [Google Scholar] [CrossRef]
  13. Rusakova, I.L. Quantum Chemical Approaches to the Calculation of NMR Parameters: From Fundamentals to Recent Advances. Magnetochemistry 2022, 8, 50. [Google Scholar] [CrossRef]
  14. Samultsev, D.O.; Semenov, V.A.; Krivdin, L.B. On the accuracy of the GIAO-DFT calculation of 15N NMR chemical shifts of the nitrogen-containing heterocycles–a gateway to better agreement with experiment at lower computational cost. Magn. Reson. Chem. 2014, 52, 222–230. [Google Scholar] [CrossRef] [PubMed]
  15. Semenov, V.A.; Samultsev, D.O.; Krivdin, L.B. Calculation of 15N NMR chemical shifts in a diversity of nitrogen-containing compounds using composite method approximation at the DFT, MP2, and CCSD levels. J. Phys. Chem. A 2019, 123, 8417–8426. [Google Scholar] [CrossRef] [PubMed]
  16. Latypov, S.K.; Kondrashova, S.A.; Polyancev, F.M.; Sinyashin, O.G. Quantum chemical calculations of 31P NMR chemical shifts in nickel complexes: Scope and limitations. Organometallics 2020, 39, 1413–1422. [Google Scholar] [CrossRef]
  17. Payard, P.-A.; Perego, L.A.; Grimaud, L.; Ciofini, I. A DFT protocol for the prediction of 31P NMR chemical shifts of phosphine ligands in first-row transition-metal complexes. Organometallics 2020, 39, 3121–3130. [Google Scholar] [CrossRef]
  18. Kazachenko, A.S.; Akman, F.; Vasilieva, N.Y.; Issaoui, N.; Malyar, Y.N.; Kondrasenko, A.A.; Borovkova, V.S.; Miroshnikova, A.V.; Kazachenko, A.S.; Al-Dossary, O.; et al. Catalytic sulfation of betulin with sulfamic acid: Experiment and DFT calculation. Int. J. Mol. Sci. 2022, 23, 1602. [Google Scholar] [CrossRef]
  19. Chan, J.C.C.; Au-Yeung, S.C.F.; Wilson, P.J.; Webb, G.A. SOS-DFPT-IGLO calculations of 59Co NMR shielding parameters of hexacoordinated diamagnetic Co(III) complexes. J. Mol. Struct. (THEOCHEM) 1996, 365, 125–130. [Google Scholar] [CrossRef]
  20. Malkin, V.G.; Malkina, O.L.; Salahub, D.R. Calculations of NMR shielding constants by uncoupled density functional theory. Chem. Phys. Lett. 1993, 204, 80–86. [Google Scholar] [CrossRef]
  21. Kofod, P. 14N NMR of amminecobalt(III) compounds. Magn. Reson. Chem. 2003, 41, 531–534. [Google Scholar] [CrossRef]
  22. Fung, B.M.; Wei, S.C. Nitrogen-14 Chemical Shifts in Cobalt(III) Complexes. J. Magn. Reson. 1970, 3, 1–4. [Google Scholar] [CrossRef]
  23. Odaka, Y.; Yamasaki, A.; Watabe, M. 15N NMR spectra of cobalt(III) complexes containing 15NO2-. Bull. Chem. Soc. Jpn. 1985, 58, 3407–3408. [Google Scholar] [CrossRef] [Green Version]
  24. Yoshiaki, N.; Masayuki, M.; Keiichi, K.; Yoshimasa, K.; Yuzo, Y. Nitrogen-15 NMR Chemical Shifts in Metal–Ammine Complexes. II. Cobalt(III) Ammine and Amine Complexes. Bull. Chem. Soc. Jpn. 1989, 62, 2455–2460. [Google Scholar] [CrossRef] [Green Version]
  25. Samultsev, D.O.; Semenov, V.A.; Krivdin, L.B. Four-component relativistic calculations of NMR shielding constants of the transition metal complexes. Part 1: Pentaammines of cobalt, rhodium and iridium. Magn. Reson. Chem. 2022, 60, 463–468. [Google Scholar] [CrossRef] [PubMed]
  26. Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
  27. Perdew, J.P.; Ernzerhof, M.; Burke, K. Rationale for mixing exact exchange with density functional approximations. J. Chem. Phys. 1996, 105, 9982–9985. [Google Scholar] [CrossRef]
  28. Nomura, Y.; Takeuchi, Y. Substituent effects in aromatic proton nmr spectra. III substituent effects caused by halogens. Tetrahedron Lett. 1969, 10, 639–642. [Google Scholar] [CrossRef]
  29. Schreckenbach, G.; Ziegler, T. Density functional calculations of NMR chemical shifts and ESR g-tensors. Theor. Chem. Acc. 1998, 99, 71–82. [Google Scholar] [CrossRef]
  30. Bühl, M.; Kaupp, M.; Malkina, O.L.; Malkin, V.G. The DFT route to NMR chemical shifts. J. Comput. Chem. 1999, 20, 91–105. [Google Scholar] [CrossRef]
  31. Chan, J.C.C.; Au-Yeung, S.C.F. A comparative study of the calculation of 59Co NMR shielding constants of hexacoordinated diamagnetic Co(III) complexes using DFT-IGLO and DFT-GIAO methods. J. Mol. Struct. (THEOCHEM) 1997, 393, 93–96. [Google Scholar] [CrossRef]
  32. Chan, J.C.C.; Au-Yeung, S.C.F. Density Functional Study of 59Co Chemical Shielding Tensors Using Gauge-Including Atomic Orbitals. J. Phys. Chem. A 1997, 101, 3637–3640. [Google Scholar] [CrossRef]
  33. Godbout, N.; Oldfield, E. Density Functional Study of Cobalt-59 Nuclear Magnetic Resonance Chemical Shifts and Shielding Tensor Elements in Co(III) Complexes. J. Am. Chem. Soc. 1997, 119, 8065–8069. [Google Scholar] [CrossRef]
  34. Xu, X.-P.; Au-Yeung, S.C.F. A DFT and 59Co Solid-State NMR Study of the Chemical Shielding Property and Electronic Interaction in the Metalloporphyrin System. J. Am. Chem. Soc. 2000, 122, 6468–6475. [Google Scholar] [CrossRef]
  35. Grigoleit, S.; Bühl, M. Computational 59Co NMR Spectroscopy:  Beyond Static Molecules. J. Chem. Theory Comput. 2005, 1, 181–193. [Google Scholar] [CrossRef] [PubMed]
  36. Ooms, K.J.; Bernard, G.M.; Kadziola, A.; Kofod, P.; Wasylishen, R.E. Solid-state 13C and 59Co NMR spectroscopy of 13C-methylcobalt(III) complexes with amine ligands. Phys. Chem. Chem. Phys. 2009, 11, 2690–2699. [Google Scholar] [CrossRef] [PubMed]
  37. Senn, F.; Zlatar, M.; Gruden-Pavlovic, M.; Daul, C. Computational analysis of tris(1,2-ethanediamine) cobalt(III) complex ion: Calculation of the 59Co shielding tensor using LF-DFT. Monatsh. Chem.–Chem. Month. 2011, 142, 593–597. [Google Scholar] [CrossRef]
  38. Kutzelnigg, W. Theory of magnetic susceptibilities and NMR chemical shifts in terms of localized quantities. Isr. J. Chem. 1980, 19, 193–200. [Google Scholar] [CrossRef]
  39. Schindler, M.; Kutzelnigg, W. Theory of magnetic susceptibilities and NMR chemical shifts in terms of localized quantities. II. Application to some simple molecules. J. Chem. Phys. 1982, 76, 1919–1933. [Google Scholar] [CrossRef]
  40. Ditchfield, R. Molecular orbital theory of magnetic shielding and magnetic susceptibility. J. Chem. Phys. 1972, 56, 5688–5693. [Google Scholar] [CrossRef]
  41. Ditchfield, R. Self-consistent perturbation theory of diamagnetism. I. A gauge-invariant LCAO method for N.M.R. chemical shifts. Mol. Phys. 1974, 27, 789–807. [Google Scholar] [CrossRef]
  42. Wolinski, K.; Hinton, J.F.; Pulay, P. Efficient implementation of the gauge-independent atomic orbital method for NMR chemical shift calculations. J. Am. Chem. Soc. 1990, 112, 8251–8260. [Google Scholar] [CrossRef]
  43. Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. 1988, 37, 785–789. [Google Scholar] [CrossRef] [Green Version]
  44. Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
  45. Malli, G.; Froese, C. Nuclear magnetic shielding constants calculated from numerical Hartree-Fock wave functions. Int. J. Quantum. Chem. 1967, 1, 95–98. [Google Scholar] [CrossRef]
  46. Wolff, S.K.; Ziegler, T.; van Lenthe, E.; Baerends, E.J. Density functional calculations of nuclear magnetic shieldings using the zeroth-order regular approximation (ZORA) for relativistic effects: ZORA nuclear magnetic resonance. J. Chem. Phys. 1999, 110, 7689–7698. [Google Scholar] [CrossRef] [Green Version]
  47. Dyall, K.G. Relativistic and nonrelativistic finite nucleus optimized double zeta basis sets for the 4p, 5p and 6p elements. Theor. Chem. Acc. 1998, 99, 366–371. [Google Scholar] [CrossRef]
  48. Dyall, K.G. Relativistic and nonrelativistic finite nucleus optimized triple-zeta basis sets for the 4p, 5p and 6p elements. Theor. Chem. Acc. 2002, 108, 335–340. [Google Scholar] [CrossRef]
  49. Jensen, F. Basis set convergence of nuclear magnetic shielding constants calculated by density functional methods. J. Chem. Theory Comp. 2008, 4, 719–727. [Google Scholar] [CrossRef] [PubMed]
  50. Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
  51. Kendall, R.A.; Dunning, T.H.; Harrison, R.J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef] [Green Version]
  52. Jensen, F. Polarization consistent basis sets: Principles. J. Chem. Phys. 2001, 115, 9113–9125. [Google Scholar] [CrossRef]
  53. Jensen, F. Polarization consistent basis sets. II. Estimating the Kohn-Sham basis set limit. J. Chem. Phys. 2002, 116, 7372–7379. [Google Scholar] [CrossRef] [Green Version]
  54. Gauss, J.; Stanton, J.F. Electron-correlated methods for the calculation of NMRchemical shifts. In Calculation of NMR and EPR Parameters, Theory and Applications, 1st ed.; Kaupp, M., Bühl, M., Malkin, V.G., Eds.; WILEY-CH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2004; Chapter 8; pp. 123–139. [Google Scholar]
  55. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  56. Tomasi, J.; Mennucci, B.; Cancès, E. The IEF version of the PCM solvation method: An overview of a new method addressed to study molecular solutes at the QM ab initio level. J. Mol. Struct. THEOCHEM 1999, 464, 211–226. [Google Scholar] [CrossRef]
  57. Tomasi, J.; Mennucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef] [PubMed]
  58. Sun, Q.; Liu, W.; Kutzelnigg, W. Comparison of restricted, unrestricted, inverse, and dual kinetic balances for four-component relativistic calculations. Theor. Chem. Acc. 2011, 129, 423–436. [Google Scholar] [CrossRef]
  59. Visscher, L. Magnetic Balance and Explicit Diamagnetic Expressions for Nuclear Magnetic Resonance Shielding Tensors. Adv. Quantum Chem. 2005, 48, 369–381. [Google Scholar] [CrossRef]
  60. Olejniczak, M.; Bast, R.; Saue, T.; Pecul, M. A simple scheme for magnetic balance in four-component relativistic Kohn−Sham calculations of nuclear magnetic resonance shielding constants in a Gaussian basis. J. Chem. Phys. 2012, 136, 014108–014111. [Google Scholar] [CrossRef] [Green Version]
  61. Iliaš, M.; Saue, T.; Enevoldsen, T.; Jensen, H.J.A. Gauge origin independent calculations of nuclear magnetic shieldings in relativistic four-component theory. J. Chem. Phys. 2009, 131, 124119. [Google Scholar] [CrossRef]
  62. Visscher, L.; Aerts, J.C.; Visser, O.; Nieuwpoort, W.C. Kinetic balance in contracted basis sets for relativistic calculations. Int. J. Quantum Chem. 1991, 40, 131–139. [Google Scholar] [CrossRef]
  63. Hartman, J.D.; Monaco, S.; Schatschneider, B.; Beran, G.J.O. Fragment-based 13C nuclear magnetic resonance chemical shift predictions in molecular crystals: An alternative to planewavemethods. J. Chem. Phys. 2015, 143, 102809. [Google Scholar] [CrossRef]
  64. Rusakov, Y.Y.; Rusakova, I.L. What Most Affects the Accuracy of 125Te NMR Chemical Shift Calculations. J. Phys. Chem. A 2020, 124, 6714–6725. [Google Scholar] [CrossRef]
  65. Semenov, V.A.; Samultsev, D.O.; Krivdin, L.B. The 1H and 13C NMR chemical shifts of strychnos alkaloids revisited at the DFT level. Magn. Reson. Chem. 2020, 58, 532–539. [Google Scholar] [CrossRef] [PubMed]
  66. Vícha, J.; Novotný, J.; Komorovsky, S.; Straka, M.; Kaupp, M.; Marek, R. Relativistic Heavy-Neighbor-Atom Effects on NMR Shifts: Concepts and Trends Across the Periodic Table. Chem. Rev. 2020, 120, 7065–7103. [Google Scholar] [CrossRef] [PubMed]
  67. Kaupp, M.; Malkina, O.L.; Malkin, V.G.; Pyykkö, P. How Do Spin-Orbit-Induced Heavy-Atom Effects on NMR Chemical Shifts Function? Validation of a Simple Analogy to Spin-Spin Coupling by Density Functional Theory (DFT) Calculations on Some Iodo Compounds. Chem. Eur. J. 1998, 4, 118–126. [Google Scholar] [CrossRef]
  68. Vícha, J.; Komorovsky, S.; Repisky, M.; Marek, R.; Straka, M. Relativistic Spin−Orbit Heavy Atom on the Light Atom NMR Chemical Shifts: General Trends Across the Periodic Table Explained. J. Chem. Theory Comput. 2018, 14, 3025–3039. [Google Scholar] [CrossRef] [PubMed]
  69. Wolff, S.K.; Ziegler, T. Calculation of DFT-GIAO NMR Shifts with the Inclusion of Spin-Orbit Coupling. J. Chem. Phys. 1998, 109, 895–905. [Google Scholar] [CrossRef]
  70. Sutter, K.; Autschbach, J. Computational Study and Molecular Orbital Analysis of NMR Shielding, Spin−Spin Coupling, and Electric Field Gradients of Azido Platinum Complexes. J. Am. Chem. Soc. 2012, 134, 13374–13385. [Google Scholar] [CrossRef]
  71. Vícha, J.; Straka, M.; Munzarová, M.L.; Marek, R. Mechanism of Spin−Orbit Effects on the Ligand NMR Chemical Shift in Transition-Metal Complexes: Linking NMR to EPR. J. Chem. Theory Comput. 2014, 10, 1489–1499. [Google Scholar] [CrossRef]
  72. Vícha, J.; Foroutan-Nejad, C.; Pawlak, T.; Munzarová, M.L.; Straka, M.; Marek, R. Understanding the Electronic Factors Responsible for Ligand Spin−Orbit NMR Shielding in Transition-Metal Complexes. J. Chem. Theory Comput. 2015, 11, 1509–1517. [Google Scholar] [CrossRef]
  73. Vícha, J.; Marek, R.; Straka, M. High-Frequency 1H NMR Chemical Shifts of SnII and PbII Hydrides Induced by Relativistic Effects: Quest for PbII Hydrides. Inorg. Chem. 2016, 55, 10302–10309. [Google Scholar] [CrossRef]
  74. Smiles, D.E.; Wu, G.; Hrobarik, P.; Hayton, T.W. Use of 77Se and 125Te NMR Spectroscopy to Probe Covalency of the ActinideChalcogen Bonding in [Th(En){N(SiMe3)2}3]− (E = Se, Te; N = 1,2) and Their Oxo-Uranium(VI) Congeners. J. Am. Chem. Soc. 2016, 138, 814–825. [Google Scholar] [CrossRef]
  75. Novotný, J.; Vícha, J.; Bora, P.L.; Repisky, M.; Straka, M.; Komorovsky, S.; Marek, R. Linking the Character of the Metal–Ligand Bond to the Ligand NMR Shielding in Transition-Metal Complexes: NMR Contributions from Spin–Orbit Coupling. J. Chem. Theory Comput. 2017, 13, 3586–3601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  76. Hrobárik, P.; Hrobárikova, V.; Meier, F.; Repiský, M.; Komorovský, S.; Kaupp, M. Relativistic Four-Component DFT Calculations of 1H NMR Chemical Shifts in Transition-Metal Hydride Complexes: Unusual High-Field Shifts Beyond the Buckingham-Stephens Model. J. Phys. Chem. A 2011, 115, 5654–5659. [Google Scholar] [CrossRef] [PubMed]
  77. Hrobárik, P.; Hrobárikova, V.; Greif, A.H.; Kaupp, M. Giant Spin-Orbit Effects on NMR Shifts in Diamagnetic Actinide Complexes: Guiding the Search of Uranium(VI) Hydride Complexes in the Correct Spectral Range. Angew. Chem. Int. Ed. 2012, 51, 10884–10888. [Google Scholar] [CrossRef] [PubMed]
  78. Greif, A.H.; Hrobárik, P.; Kaupp, M. Insights into trans-Ligand and Spin-Orbit Effects on Electronic Structure and Ligand NMR Shifts in Transition-Metal Complexes. Chem. Eur. J. 2017, 23, 9790–9803. [Google Scholar] [CrossRef] [PubMed]
  79. Greif, A.H.; Hrobárik, P.; Hrobárikova, V.; Arbuznikov, A.V.; Autschbach, J.; Kaupp, M. A Relativistic Quantum-Chemical Analysis of the trans Influence on 1H NMR Hydride Shifts in Square-Planar Platinum(II) Complexes. Inorg. Chem. 2015, 54, 7199–7208. [Google Scholar] [CrossRef] [PubMed]
  80. Bagno, A.; Saielli, G. Relativistic DFT calculations of the NMR properties and reactivity of transition metal methane σ-complexes: Insights on C–H bond activation. Phys. Chem. Chem. Phys. 2011, 13, 4285–4291. [Google Scholar] [CrossRef] [PubMed]
  81. Ruiz-Morales, Y.; Schreckenbach, G.; Ziegler, T. Origin of the Hydridic 1H NMR Chemical Shift in Low-Valent Transition-Metal Hydrides. Organometallics 1996, 15, 3920–3923. [Google Scholar] [CrossRef]
  82. Harris, R.K.; Becker, E.D.; de Menezes, S.M.C.; Goodfellow, R.; Granger, P. NMR nomenclature. Nuclear spin properties andconventions for chemical shifts (IUPAC Recommendations 2001). Pure Appl. Chem. 2001, 73, 795–1818. [Google Scholar] [CrossRef]
  83. Harris, R.K.; Becker, E.D.; de Menezes, S.M.C.; Granger, P.; Hoffman, R.E.; Zilm, K.W. Further conventions for NMR shielding and chemical shifts (IUPAC Recommendations 2008). Pure Appl. Chem. 2008, 80, 59–84. [Google Scholar] [CrossRef]
  84. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B. GAUSSIAN 09; Revision, C.01; Gaussian, Inc.: Wallingford, CT, USA, 2009; Available online: http://www.gaussian.com (accessed on 1 September 2022).
  85. Semenov, V.A.; Samultsev, D.O.; Rusakova, I.L.; Krivdin, L.B. Computational multinuclear NMR of platinum complexes: A relativistic four-component study. J. Phys. Chem. A 2019, 123, 4908–4920. [Google Scholar] [CrossRef]
  86. Jensen, H.J.A.; Bast, R.; Saue, T.; Visscher, L. DIRAC 16. Revision 2016. Available online: http://www.diracprogram.org (accessed on 1 September 2022).
  87. Mao, Y.; Horn, P.R.; Mardirossian, N.; Head-Gordon, T.; Skylaris, C.-K.; Head-Gordon, M. Approaching the basis set limit for DFT calculations using an environment-adapted minimal basis with perturbation theory: Formulation, proof of concept, and a pilot implementation. J. Chem. Phys. 2016, 145, 044109. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  88. Burke, K. Perspective on density functional theory. J. Chem. Phys. 2012, 136, 150901. [Google Scholar] [CrossRef] [PubMed]
  89. Lutnæs, O.B.; Helgaker, T.; Jaszuński, M. Spin–spin coupling constants and triplet instabilities in Kohn–Sham theory. Mol. Phys. 2010, 108, 2579–2590. [Google Scholar] [CrossRef]
  90. Labanowski, J.K.; Andxelm, J.W. Density Function Methods in Chemistry; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
  91. Adamo, C.; Barone, V. Toward chemical accuracy in the computation of NMR shieldings: The PBE0 model. Chem. Phys. Lett. 1998, 298, 113–119. [Google Scholar] [CrossRef]
  92. de Giovanetti, M.; Bitencourt, L.F.F.; Cormanich, R.; Sauer, S.P.A. On the Unexpected Accuracy of the M06L Functional in the Calculation of 1JFC Spin–Spin Coupling Constants. J. Chem. Thery Comput. 2021, 17, 7712–7723. [Google Scholar] [CrossRef]
  93. Manninen, P.; Lantto, P.; Vaara, J.; Ruud, K. Perturbational ab initio calculations of relativistic contributions to nuclear magnetic resonance shielding tensors. J. Chem. Phys. 2003, 119, 2623–2637. [Google Scholar] [CrossRef]
  94. Manninen, P.; Ruud, K.; Lantto, P.; Vaara, J. Leading-order relativistic effects on nuclear magnetic resonance shielding tensors. J. Chem. Phys. 2005, 122, 114107. [Google Scholar] [CrossRef]
Ijms 23 13178 g001a 550Ijms 23 13178 g001b 550
Figure 1. Equilibrium geometries of the nitrogen-coordinated cobalt complexes 1–27, obtained at the PBE0/ATZP level of theory.
Figure 1. Equilibrium geometries of the nitrogen-coordinated cobalt complexes 1–27, obtained at the PBE0/ATZP level of theory.
Ijms 23 13178 g001aIjms 23 13178 g001b
Ijms 23 13178 g002 550
Figure 2. Convergence of the 15N NMR shielding constant of [Co(NH3)6]3+ to the c∞ limit in the GIAO-4DFT-PBE0/BaS(uc) calculation.
Figure 2. Convergence of the 15N NMR shielding constant of [Co(NH3)6]3+ to the c∞ limit in the GIAO-4DFT-PBE0/BaS(uc) calculation.
Ijms 23 13178 g002
Ijms 23 13178 g003 550
Figure 3. Correlation plot of calculated 15N NMR chemical shifts (ppm) versus experiment.
Figure 3. Correlation plot of calculated 15N NMR chemical shifts (ppm) versus experiment.
Ijms 23 13178 g003
Ijms 23 13178 g004 550
Figure 4. Relativistic corrections to the 15N shielding constants, ppm.
Figure 4. Relativistic corrections to the 15N shielding constants, ppm.
Ijms 23 13178 g004
Ijms 23 13178 g005 550
Figure 5. Solvent corrections to the 15N NMR shielding constants, ppm.
Figure 5. Solvent corrections to the 15N NMR shielding constants, ppm.
Ijms 23 13178 g005
Ijms 23 13178 g006 550
Figure 6. Convergence to the c∞ limit for the 59Co NMR shielding constant in [Co(CN)6]3− in the framework of the GIAO-4DFT-PBE0/BaS(uc) calculation.
Figure 6. Convergence to the c∞ limit for the 59Co NMR shielding constant in [Co(CN)6]3− in the framework of the GIAO-4DFT-PBE0/BaS(uc) calculation.
Ijms 23 13178 g006
Ijms 23 13178 g007 550
Figure 7. Relativistic corrections to the 59Co NMR shielding constants, ppm.
Figure 7. Relativistic corrections to the 59Co NMR shielding constants, ppm.
Ijms 23 13178 g007
Ijms 23 13178 g008 550
Figure 8. Solvent corrections to the 59Co shielding constants, ppm.
Figure 8. Solvent corrections to the 59Co shielding constants, ppm.
Ijms 23 13178 g008
Table
Table 1. 15N NMR shielding constants and chemical shifts (both in ppm) of amino groups in 1–27 calculated at the GIAO-DFT-PBE0 nonrelativistic and four-component relativistic levels of theory.
Table 1. 15N NMR shielding constants and chemical shifts (both in ppm) of amino groups in 1–27 calculated at the GIAO-DFT-PBE0 nonrelativistic and four-component relativistic levels of theory.
Cmpd.FormulaσGPΔsolvΔrelσtotδtot1δexp2
trans
1[Co(NH3)5F]2+283.83.23.8290.8−426.2−451.2
2[Co(NH3)5Cl]2+271.6−11.711.1271.0−408.2−434.9
3[Co(NH3)5Br]2+266.2−2.813.7277.1−413.8-
4[Co(NH3)5I]2+256.51.615.3273.4−410.4-
5[Co(NH3)5CH3]2+249.51.7−1.6249.6−388.9−382.0
6[Co(NH3)5CN]2+257.12.2−11.8247.5−387.0−401.8
[Co(NH3)5CN]2+−174.863.210.0−101.6−70.9-
7[Co(NH3)5NO2]2+273.03.512.2288.7−424.3−416.1
[Co(NH3)5NO2]2+−239.0−34.665.0−208.726.0-
8[Co(NH3)5OH]2+273.52.715.0291.2−426.6−429.2
9[Co(NH3)5N3]2+269.65.112.8287.5−423.2−430.3
[Co(NH3)5(N=N=N)]2+210.62.6−11.3201.9−345.7-
[Co(NH3)5(N=N=N)]2+−17.1−5.5−0.7−23.4−141.7-
[Co(NH3)5(N=N=N)]2+33.050.2−5.977.3−232.8-
10[Co(NH3)5CO3]+270.09.00.4279.4−415.9−437.5
11[Co(NH3)5H2O]3+298.2−1.517.1313.8−447.0−447.0
12cis-[Co(NH3)4(NO2)2]+269.84.217.2291.2−426.5−416.0
cis-[Co(NH3)4(NO2)2]+−254.0−25.361.2−218.134.6-
13cis-[Co(NH3)4CO3]+267.16.011.6284.7−420.6−436.7
14cis-[Co(NH3)4(H2O)Cl]+ to H2O282.9−0.324.2306.8−440.7−445.2
cis-[Co(NH3)4(H2O)Cl]+ to Cl262.74.815.8283.3−419.4−431.0
15cis-[Co(NH3)4(H2O)2]3+287.4−1.220.3306.5−440.4−444.0
16mer-[Co(NH3)3(NO2)3]3+264.76.220.0290.9−426.2−412.2
mer-[Co(NH3)3(NO2)3]3+ to NO2−−290.2−6.638.9−257.970.6-
mer-[Co(NH3)3(NO2)3]3+ to NH3−262.9−18.751.2−230.445.7-
17fac-[Co(NH3)3(NO2)3]3+245.81.912.9260.6−398.8-
fac-[Co(NH3)3(NO2)3]3+−282.6−18.649.9−251.364.6-
18mer-[Co(NH3)3(H2O)3]3+281.8−1.238.3318.9−451.6−443.3
19fac-[Co(NH3)3(H2O)3]3+287.4−1.528.5314.4−447.5-
20cis-[Co(NH3)2(NO2)4]−232.82.412.4247.6−387.1-
cis-[Co(NH3)2(NO2)4]− to NO2−−303.8−4.141.3−266.678.5-
cis-[Co(NH3)2(NO2)4]− to NH3−279.7−15.344.0−251.064.4-
21cis-[Co(NH3)2(CO3)2]−254.78.550.6313.8−447.0−436.7
22cis,mer-[Co(NH3)2(NO2)3CH3]− to NO2−238.45.231.5275.1−411.9-
cis,mer-[Co(NH3)2(NO2)3CH3]− to CH3226.91.2−10.9217.2−359.5-
cis,mer-[Co(NH3)2(NO2)3CH3]− to NO2−337.2−7.473.8−270.882.3-
cis,mer-[Co(NH3)2(NO2)3CH3]− to NH3−304.2−20.443.8−280.891.3-
23cis,fac-[Co(NH3)2(NO2)3CH3]−240.55.518.3264.3−402.2-
cis,fac-[Co(NH3)2(NO2)3CH3]− to CH3−334.8−12.417.0−330.2136.1-
cis,fac-[Co(NH3)2(NO2)3CH3]− to NH3−305.9−19.044.4−280.591.1-
24trans,mer-[Co(NH3)2(NO2)3CH3]− to NO2−−322.0−7.339.3−290.099.7-
trans,mer-[Co(NH3)2(NO2)3CH3]− to CH3−318.8−9.117.8−310.1117.9-
cis
1[Co(NH3)5F]2+256.1−1.220.3275.2−412.0−417.5
2[Co(NH3)5Cl]2+260.3−0.424.1284−420.0−419.9
3[Co(NH3)5Br]2+264.010.425.5299.9−434.4-
4[Co(NH3)5I]2+258.13.924.2286.2−422.0-
5[Co(NH3)5CH3]2+268.9−0.324.3292.9−428.1−428.8
6[Co(NH3)5CN]2+271.01.0−19.2252.8−391.8−425.9
7[Co(NH3)5NO2]2+261.33.922.2287.4−423.1−416.1
8[Co(NH3)5OH]2+255.7−1.020.1274.8−411.7−419.2
9[Co(NH3)5N3]2+261.00.922.5284.4−420.4−422.2
10[Co(NH3)5CO3]+254.10.326.6281.0−417.3−419.1
11[Co(NH3)5H2O]3+271.0−1.326.8296.5−431.3−420.1
12cis-[Co(NH3)4(NO2)2]+239.12.314.7256.1−394.7−401.8
13cis-[Co(NH3)4CO3]+256.8−1.320.4275.9−412.7−416.7
14cis-[Co(NH3)4(H2O)Cl]+260.4−0.923.9283.4−419.5−417.2
15cis-[Co(NH3)4(H2O)2]3+266.4−1.128.7294.0−429.1−416.6
16mer-[Co(NH3)3(NO2)3]3+228.42.113.7244.2−384.0−393.2
18mer-[Co(NH3)3(H2O)3]3+261.9−1.417.3277.8−414.4−413.4
24trans,mer-[Co(NH3)2(NO2)3CH3]−237.62.616.5256.7−395.3−397.5
25[Co(NH3)6]3+271.7−0.926.1296.9−431.7−422.8
26trans-[Co(NH3)4(NO2)2]+251.92.520.3274.7−411.6−409.0
trans-[Co(NH3)4(NO2)2]+−279.2−9.634.1−254.767.8-
27trans-[Co(NH3)2(NO2)4]−223.90.812.3237.0−377.5−381.1
trans-[Co(NH3)2(NO2)4]−−291.2−1.640.1−252.765.9-
1 Linear regression equation: δ = σ − B A , B = −179.90, A = −1.1045. The points of [Co(NH3)5F]2+ (trans-orientation), [Co(NH3)5Cl]2+ (trans-orientation), [Co(NH3)5CN]2+ (cis-orientation) and [Co(NH3)5CO3]+ (trans-orientation) were excluded when evaluating the parameters of the linear regression model. 2 Experimental values were taken from Ref. [21].
Table
Table 2. 59Co NMR shielding constants and chemical shifts (ppm) of 1–27, calculated at the GIAO-DFT-PBE0/BaS nonrelativistic and four-component relativistic levels of theory.
Table 2. 59Co NMR shielding constants and chemical shifts (ppm) of 1–27, calculated at the GIAO-DFT-PBE0/BaS nonrelativistic and four-component relativistic levels of theory.
Cmpd.FormulaσnrσrelΔrelσ 1Δsolvσ 2σtot 3δnr 4δrel 5Δrelδ 6Δsolvδ 7δtot 8
1[Co(NH3)5F]2+−10,394.4−10,039.7354.7−221.1−15,963.43675.13550.2−124.8230.93781.1
2[Co(NH3)5Cl]2+−14,224.8−13,813.3411.5−351.9−15,479.77505.47323.8−181.6361.77685.5
3[Co(NH3)5Br]2+−15,554.1−15,102.6451.5−496.5−15,560.08834.88613.1−221.7506.39119.4
4[Co(NH3)5I]2+−15,124.0−14,715.5408.5−403.4−13,126.68404.78226.0−178.7413.28639.2
5[Co(NH3)5CH3]2+−14,331.6−13,440.4891.2−132.8−13,538.37612.36951.0−661.3142.67093.6
6[Co(NH3)5CN]2+−12,300.9−11,850.6450.3120.1−13,199.35581.65361.1−220.4−110.25250.9
7[Co(NH3)5NO2]2+−15,244.7−14,681.2563.5−207.4−14,586.58525.48191.7−333.6217.28409.0
8[Co(NH3)5OH]2+−16,051.5−15,397.3654.2−198.4−15,265.49332.18907.8−424.3208.29116.0
9[Co(NH3)5N3]2+−15,959.8−15,200.1759.7−279.8−15,103.99240.58710.7−529.8289.69000.3
10[Co(NH3)5CO3]+−16,649.2−15,473.81175.4−180.3−15,008.29929.98984.4−945.5190.19174.5
11[Co(NH3)5H2O]3+−19,128.1−18,236.5891.6−274.8−18,393.912,408.811,747.0−661.8284.612,031.6
12cis-[Co(NH3)4(NO2)2]+−14,130.2−13,662.1468.1−209.8−13,621.57410.97172.7−238.2219.77392.3
13cis-[Co(NH3)4CO3]+−15,914.4−15,255.3659.1−418.3−15,249.19195.08765.8−429.3428.29194.0
14cis-[Co(NH3)4(H2O)Cl]+−17,032.5−16,333.1699.3−242.1−16,271.410,313.19843.7−469.5251.910,095.6
15cis-[Co(NH3)4(H2O)2]3+−18,696.1−17,945.5750.6−252.9−17,942.911,976.811,456.0−520.8262.711,718.7
16mer-[Co(NH3)3(NO2)3]3+−13,349.6−12,947.8401.8−7.1−12,806.96630.36458.4−171.917.06475.4
17fac-[Co(NH3)3(NO2)3]3+−13,740.3−13,375.0365.3−50.4−13,279.27021.06885.6−135.560.26945.8
18mer-[Co(NH3)3(H2O)3]3+−21,251.8−19,978.91272.8−311.7−20,157.414,532.513,489.5−1043.0321.513,810.9
19fac-[Co(NH3)3(H2O)3]3+−19,478.0−18,746.8731.2−242.4−18,809.312,758.712,257.4−501.3252.212,509.6
20cis-[Co(NH3)2(NO2)4]−−13,551.3−13,204.7346.7105.0−13,015.06832.06715.2−116.8−95.26620.0
21cis-[Co(NH3)2(CO3)2]−−18,115.3−16,493.31622.0−209.6−16,275.411,396.010,003.8−1392.1219.410,223.2
22cis,mer-[Co(NH3)2(NO2)3CH3]−−12,948.1−12,188.7759.4−63.5−12,219.86228.85699.2−529.673.45772.6
23cis,fac-[Co(NH3)2(NO2)3CH3]−−12,684.5−12,287.6396.9221.1−12,057.45965.25798.1−167.1−211.35586.8
24trans,mer-[Co(NH3)2(NO2)3CH3]−−11,844.1−11,475.9368.2132.2−11,372.55124.84986.5−138.3−122.34864.1
25[Co(NH3)6]3+−15,961.7−15,470.5491.2−232.2−15,667.99242.48981.1−261.4242.09223.1
26trans-[Co(NH3)4(NO2)2]+−14,042.9−13,548.9494.067.4−13,283.87323.57059.4−264.1−57.67001.9
27trans-[Co(NH3)2(NO2)4]−−13,131.6−12,790.0341.646.7−12,664.66412.36300.5−111.7−36.96263.6
1 Δrelσ = σrel − σnr; 2 Δsolvσ = σsolv − σGP; 3 σtot = σGP + Δrelσ + Δsolvσ; 4 δnr = σnr(ref) − σnr; 5 δrel = σrel(ref) − σrel; 6 Δrelδ = δrel − δnr ≡ Δrelσ(ref) − Δrelσ; 7 Δsolvδ = δsolv − δGP ≡ Δsolvσ(ref) − Δsolvσ; 8 δtot = δrel + Δsolvδ ≡ δnr + Δrelδ + Δsolvδ = σtot(ref) − σtot.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Samultsev, D.O.; Semenov, V.A.; Rusakova, I.L.; Krivdin, L.B. Four-Component Relativistic Calculations of NMR Shielding Constants of the Transition Metal Complexes—Part 2: Nitrogen-Coordinated Complexes of Cobalt. Int. J. Mol. Sci. 2022, 23, 13178. https://doi.org/10.3390/ijms232113178

AMA Style

Samultsev DO, Semenov VA, Rusakova IL, Krivdin LB. Four-Component Relativistic Calculations of NMR Shielding Constants of the Transition Metal Complexes—Part 2: Nitrogen-Coordinated Complexes of Cobalt. International Journal of Molecular Sciences. 2022; 23(21):13178. https://doi.org/10.3390/ijms232113178

Chicago/Turabian Style

Samultsev, Dmitry O., Valentin A. Semenov, Irina L. Rusakova, and Leonid B. Krivdin. 2022. "Four-Component Relativistic Calculations of NMR Shielding Constants of the Transition Metal Complexes—Part 2: Nitrogen-Coordinated Complexes of Cobalt" International Journal of Molecular Sciences 23, no. 21: 13178. https://doi.org/10.3390/ijms232113178

APA Style

Samultsev, D. O., Semenov, V. A., Rusakova, I. L., & Krivdin, L. B. (2022). Four-Component Relativistic Calculations of NMR Shielding Constants of the Transition Metal Complexes—Part 2: Nitrogen-Coordinated Complexes of Cobalt. International Journal of Molecular Sciences, 23(21), 13178. https://doi.org/10.3390/ijms232113178

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop