Ionic Mechanisms of Propagated Repolarization in a One-Dimensional Strand of Human Ventricular Myocyte Model
Abstract
:1. Introduction
2. Results
2.1. Threshold Potentials for the All-or-None Repolarization in the hVC Model
2.2. Ionic Mechanisms Responsible for Determining the Threshold Potentials for All-or-None Repolarization
2.3. Induction of a Stable Equilibrium Potential in the Current-Voltage Relationship of the hVC Model
2.4. Propagation of Repolarization from the Second Stable Equilibrium Potential at Around 0 mV
2.5. Effects of Varying the Conductance of INaL, IK1, and Gap Junction Channel (Gg) on the Rate of Propagation of Repolarization
3. Discussion
3.1. Brief Summary of the Results
- (1)
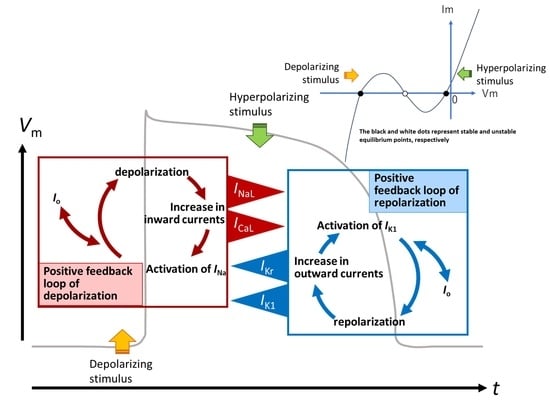
- The ionic mechanisms underlying the induced all-or-none repolarization at the myocyte level (Figure 2), and the propagation of repolarization in a 1D linear strand of myocytes (Figure 4), were examined. Unambiguous propagation of repolarization that did not overlap with the natural time course of the AP plateau was observed only when the 1D strand of myocytes was depolarized at the second stable equilibrium potential, which was introduced by freezing the fraction of slow inactivation of INaL to 0.451 in Figure 4.
- (2)
- The key ionic currents were IK1, IKr, INaL, and ICaL in both the abolition of the AP plateau in a single ventricular myocyte and the propagation of repolarization in the in silico 1D strand of the myocyte model. Since the voltage range of the kinetic dynamics for IK1 and INaL are more negative compared to that for IKr and ICaL, as demonstrated in Figure 3A, IK1 and INaL play their role during the late phase of repolarization, while IKr and ICaL work in the early phase of repolarization. The positive feedback mechanisms accelerate the rate of Vm change caused by the kinetics dynamics of these currents.
- (3)
- In the abolition experiments in Figure 1 and Figure 2, the triggering pulse of hyperpolarization was supplied by the external current source, while the propagation of repolarization in the 1D strand was initiated by local current Io and evoked by the myocytes located behind the wavefront of repolarization before the O/I center (Figure 4D2).
- (4)
- The kinetic mechanisms of the four currents were most probably responsible for the stable propagation of repolarization.
- (5)
- The O/I profile of Vo around the O/I center (Figure 4D2) is a mirror image of that in the propagation of excitation (Figure 4B, inset). The width of the O/I profile was much more elongated in the propagation of repolarization (Figure 4D1–D5) compared with that for the propagation of AP (Figure 4B), reflecting the relatively small current amplitude of IK1, INaL, IKr, and ICaL in repolarization. The merit of using multiple channel species may be attributed to its flexibility in adjusting the configuration of the AP plateau phase more precisely and stably.
- (6)
- The rate of propagation of repolarization was dependent mainly on the amplitude of IK1 and INaL (Table 1). The rate increased with increasing the Gg within a limited range of Gg.
3.2. Clinical Implications
3.3. Ionic Mechanisms of Propagation of Repolarization in Comparison to the Propagation of Excitation
4. Materials and Methods
4.1. The hVC Model
4.2. One-Dimensional Strand of the hVC Model
4.3. Calculating Vo Outside the Myocyte Membrane in the Strand
| Algorithm 1. Summary of the calculation for the 1D myocyte strand model. |
| Step1: Calculate conductance matrix of A, B, C in Equation (9); |
| Step2: Calculate the inverse matrix of the conductance matrix of A, B, C; |
| Step3: Calculate the right-hand side of Equation (9) from ; |
| Step4 in Equation (9) by using the inverse matrix obtained in Step 2; |
| Step5 using Equation (5); |
| Step6 using Equation (6); |
| Step7 using Equation (7); |
| Step8 ; |
| Step9: Integration of parameters for the next time step ; |
| Step10: Go to Step3. |
4.4. Electrical Stimulation to the Myocyte Model and the Myocyte Strand Model
4.5. Induction of the Second Stable Equilibrium Vm in Myocyte Model within the In Silico 1D Strand
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References and Note
- Noble, D. A modification of the Hodgkin-Huxley equations applicable to Purkinje fibre action and pacemaker potentials. J. Physiol. 1962, 160, 317–352. [Google Scholar] [CrossRef] [PubMed]
- Trenor, B.; Cardona, K.; Saiz, J.; Noble, D.; Giles, W. Cardiac action potential repolarization revisited: Early repolarization shows all-or-none behaviour. J. Physiol. 2017, 595, 6599–6612. [Google Scholar] [CrossRef] [PubMed]
- Noble, D.; Hall, A.E. The Conditions for Initiating “All-or-Nothing” Repolarization in Cardiac Muscle. Biophys. J. 1963, 3, 261–274. [Google Scholar] [CrossRef] [PubMed]
- Noble, D. The voltage dependence of the cardiac membrane conductance. Biophys. J. 1962, 2, 381–393. [Google Scholar] [CrossRef] [PubMed]
- Weidmann, S. Effect of current flow on the membrane potential of cardiac muscle. J. Physiol. 1951, 115, 227–236. [Google Scholar] [CrossRef] [PubMed]
- Cranefield, P.F.; Hoffman, B.F. Propagated repolarization in heart muscle. J. Gen. Physiol. 1958, 41, 633–649. [Google Scholar] [CrossRef] [PubMed]
- Powell, T.; Steen, E.M.; Twist, V.W.; Woolf, N. Surface characteristics of cells isolated from adult rat myocardium. J. Mol. Cell. Cardiol. 1978, 10, 287–292. [Google Scholar] [CrossRef]
- Powell, T.; Twist, V.W. A rapid technique for the isolation and purification of adult cardiac muscle cells having respiratory control and a tolerance to calcium. Biochem. Biophys. Res. Commun. 1976, 72, 327–333. [Google Scholar] [CrossRef]
- Powell, T.; Terrar, D.A.; Twist, V.W. Electrical properties of individual cells isolated from adult rat ventricular myocardium. J. Physiol. 1980, 302, 131–153. [Google Scholar] [CrossRef]
- Sakmann, B.; Neher, E. Patch clamp techniques for studying ionic channels in excitable membranes. Annu. Rev. Physiol. 1984, 46, 455–472. [Google Scholar] [CrossRef]
- Fink, M.; Niederer, S.A.; Cherry, E.M.; Fenton, F.H.; Koivumäki, J.T.; Seemann, G.; Thul, R.; Zhang, H.; Sachse, F.B.; Beard, D.; et al. Cardiac cell modelling: Observations from the heart of the cardiac physiome project. Prog. Biophys. Mol. Biol. 2011, 104, 2–21. [Google Scholar] [CrossRef] [PubMed]
- O’Hara, T.; Virág, L.; Varró, A.; Rudy, Y. Simulation of the undiseased human cardiac ventricular action potential: Model formulation and experimental validation. PLoS Comput. Biol. 2011, 7, e1002061. [Google Scholar] [CrossRef]
- Grandi, E.; Pasqualini, F.S.; Bers, D.M. A novel computational model of the human ventricular action potential and Ca transient. J. Mol. Cell. Cardiol. 2010, 48, 112–121. [Google Scholar] [CrossRef] [PubMed]
- Asakura, K.; Cha, C.Y.; Yamaoka, H.; Horikawa, Y.; Memida, H.; Powell, T.; Amano, A.; Noma, A. EAD and DAD mechanisms analyzed by developing a new human ventricular cell model. Prog. Biophys. Mol. Biol. 2014, 116, 11–24. [Google Scholar] [CrossRef]
- Himeno, Y.; Asakura, K.; Cha, C.Y.; Memida, H.; Powell, T.; Amano, A.; Noma, A. A human ventricular myocyte model with a refined representation of excitation-contraction coupling. Biophys. J. 2015, 109, 415–427. [Google Scholar] [CrossRef] [PubMed]
- Undrovinas, A.I.; Maltsev, V.A.; Kyle, J.W.; Silverman, N.; Sabbah, H.N. Gating of the late Na+ channel in normal and failing human myocardium. J. Mol. Cell. Cardiol. 2002, 34, 1477–1489. [Google Scholar] [CrossRef]
- Näbauer, M.; Beuckelmann, D.J.; Uberfuhr, P.; Steinbeck, G. Regional differences in current density and rate-dependent properties of the transient outward current in subepicardial and subendocardial myocytes of human left ventricle. Circulation 1996, 93, 168–177. [Google Scholar] [CrossRef]
- Chandler, W.K.; Meves, H. Slow changes in membrane permeability and long-lasting action potentials in axons perfused with fluoride solutions. J. Physiol. 1970, 211, 707–728. [Google Scholar] [CrossRef]
- Undrovinas, A.I.; Fleidervish, I.A.; Makielski, J.C. Inward sodium current at resting potentials in single cardiac myocytes induced by the ischemic metabolite lysophosphatidylcholine. Circ. Res. 1992, 71, 1231–1241. [Google Scholar] [CrossRef] [PubMed]
- Qu, Z.; Xie, L.H.; Olcese, R.; Karagueuzian, H.S.; Chen, P.S.; Garfinkel, A.; Weiss, J.N. Early afterdepolarizations in cardiac myocytes: Beyond reduced repolarization reserve. Cardiovasc. Res. 2013, 99, 6–15. [Google Scholar] [CrossRef]
- Himeno, Y. Ritsumeikan University, Shiga, Japan. Our simulation using a strand composed of intact hVC demonstrated that it was impossible to determine a unique value for the velocity of propagated repolarization because the velocity increased continuously and approached infinity as the repolarization propagated. 2023.
- Kirkton, R.D.; Badie, N.; Bursac, N. Spatial Profiles of Electrical Mismatch Determine Vulnerability to Conduction Failure Across a Host–Donor Cell Interface. Circ. Arrhythm. Electrophysiol. 2013, 6, 1200–1207. [Google Scholar] [CrossRef] [PubMed]
- Sperelakis, N.; Ramasamy, L.; Kalloor, B. Propagated repolarization of simulated action potentials in cardiac muscle and smooth muscle. Theor. Biol. Med. Model 2005, 2, 5. [Google Scholar] [CrossRef]
- Yan, D.H.; Ishihara, K. Two Kir2.1 channel populations with different sensitivities to Mg2+ and polyamine block: A model for the cardiac strong inward rectifier K+ channel. J. Physiol. 2005, 563, 725–744. [Google Scholar] [CrossRef] [PubMed]
- Ishihara, K.; Sarai, N.; Asakura, K.; Noma, A.; Matsuoka, S. Role of Mg2+ block of the inward rectifier K+ current in cardiac repolarization reserve: A quantitative simulation. J. Mol. Cell. Cardiol. 2009, 47, 76–84. [Google Scholar] [CrossRef]
- Fabbri, A.; Goversen, B.; Vos, M.A.; van Veen, T.A.B.; de Boer, T.P. Required GK1 to Suppress Automaticity of iPSC-CMs Depends Strongly on IK1 Model Structure. Biophys. J. 2019, 117, 2303–2315. [Google Scholar] [CrossRef] [PubMed]
- Taggart, P.; Sutton, P.; John, R.; Hayward, R.; Swanton, H. The epicardial electrogram: A quantitative assessment during balloon angioplasty incorporating monophasic action potential recordings. Br. Heart J. 1989, 62, 342–352. [Google Scholar] [CrossRef]
- Shannon, T.R.; Wang, F.; Puglisi, J.; Weber, C.; Bers, D.M. A mathematical treatment of integrated Ca dynamics within the ventricular myocyte. Biophys. J. 2004, 87, 3351–3371. [Google Scholar] [CrossRef]
- Negroni, J.A.; Lascano, E.C. Simulation of steady state and transient cardiac muscle response experiments with a Huxley-based contraction model. J. Mol. Cell. Cardiol. 2008, 45, 300–312. [Google Scholar] [CrossRef]
- Rush, S.; Larsen, H. A practical algorithm for solving dynamic membrane equations. IEEE Trans. Biomed. Eng. 1978, 25, 389–392. [Google Scholar] [CrossRef]
- Ishihara, K.; Yan, D.H. Low-affinity spermine block mediating outward currents through Kir2.1 and Kir2.2 inward rectifier potassium channels. J. Physiol. 2007, 583, 891–908. [Google Scholar] [CrossRef]
- Takeuchi, A.; Tatsumi, S.; Sara, N.; Terashima, K.; Matsuoka, S.; Noma, A. Ionic mechanisms of cardiac cell swelling induced by blocking Na+/K+ pump as revealed by experiments and simulation. J. Gen. Physiol. 2006, 128, 495–507. [Google Scholar] [CrossRef]
- Oka, C.; Cha, C.Y.; Noma, A. Characterization of the cardiac Na+/K+ pump by development of a comprehensive and mechanistic model. J. Theor. Biol. 2010, 265, 68–77. [Google Scholar] [CrossRef] [PubMed]
- Smith, N.P.; Crampin, E.J. Development of models of active ion transport for whole-cell modelling: Cardiac sodium-potassium pump as a case study. Prog. Biophys. Mol. Biol. 2004, 85, 387–405. [Google Scholar] [CrossRef] [PubMed]
- Grandi, E.; Pasqualini, F.S.; Pes, C.; Corsi, C.; Zaza, A.; Severi, S. Theoretical investigation of action potential duration dependence on extracellular Ca2+ in human cardiomyocytes. J. Mol. Cell. Cardiol. 2009, 46, 332–342. [Google Scholar] [CrossRef] [PubMed]
- Hinch, R.; Greenstein, J.L.; Tanskanen, A.J.; Xu, L.; Winslow, R.L. A simplified local control model of calcium-induced calcium release in cardiac ventricular myocytes. Biophys. J. 2004, 87, 3723–3736. [Google Scholar] [CrossRef]
- Tran, K.; Smith, N.P.; Loiselle, D.S.; Crampin, E.J. A thermodynamic model of the cardiac sarcoplasmic/endoplasmic Ca2+ (SERCA) pump. Biophys. J. 2009, 96, 2029–2042. [Google Scholar] [CrossRef]





| 0.639 (−20%) | 0.594 (−10%) | Relative GNaL 0.549 after Fixing (I2 + Is) | 0.504 (+10%) | 0.459 (+20%) | |
|---|---|---|---|---|---|
| −10% | F | F | F | F | F |
| control GK1 | F | F | F | 1.69 | 2.11 |
| +10% | F | 1.52 | 1.94 | 2.38 | 2.94 |
| +20% | 1.79 | 2.114 | 2.40 | 2.69 | 3.04 |
| Gg (nS) | 1000 | 1500 | 2000 | 2500 |
| rate excitation propagation (cm/s) | 36.5 | 48.0 | 51.79 | 58.5 |
| rate repolarization propagation (cm/s) | 1.93 | 2.43 | 2.60 | 2.94 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Himeno, Y.; Zhang, Y.; Enomoto, S.; Nomura, H.; Yamamoto, N.; Kiyokawa, S.; Ujihara, M.; Muangkram, Y.; Noma, A.; Amano, A. Ionic Mechanisms of Propagated Repolarization in a One-Dimensional Strand of Human Ventricular Myocyte Model. Int. J. Mol. Sci. 2023, 24, 15378. https://doi.org/10.3390/ijms242015378
Himeno Y, Zhang Y, Enomoto S, Nomura H, Yamamoto N, Kiyokawa S, Ujihara M, Muangkram Y, Noma A, Amano A. Ionic Mechanisms of Propagated Repolarization in a One-Dimensional Strand of Human Ventricular Myocyte Model. International Journal of Molecular Sciences. 2023; 24(20):15378. https://doi.org/10.3390/ijms242015378
Chicago/Turabian StyleHimeno, Yukiko, Yixin Zhang, Suzuka Enomoto, Hiroto Nomura, Natsuki Yamamoto, Shotaro Kiyokawa, Mirei Ujihara, Yuttamol Muangkram, Akinori Noma, and Akira Amano. 2023. "Ionic Mechanisms of Propagated Repolarization in a One-Dimensional Strand of Human Ventricular Myocyte Model" International Journal of Molecular Sciences 24, no. 20: 15378. https://doi.org/10.3390/ijms242015378
APA StyleHimeno, Y., Zhang, Y., Enomoto, S., Nomura, H., Yamamoto, N., Kiyokawa, S., Ujihara, M., Muangkram, Y., Noma, A., & Amano, A. (2023). Ionic Mechanisms of Propagated Repolarization in a One-Dimensional Strand of Human Ventricular Myocyte Model. International Journal of Molecular Sciences, 24(20), 15378. https://doi.org/10.3390/ijms242015378