Molecular Dynamics Simulations of Claudin-10a and -10b Ion Channels: With Similar Architecture, Different Pore Linings Determine the Opposite Charge Selectivity
Abstract
:1. Introduction
2. Results
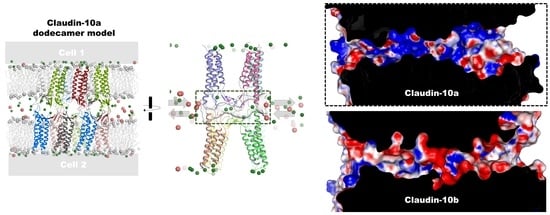
2.1. Generation of Dodecamer Model for CLDN10a
2.2. Evaluation of the CLDN10a Dodecamer Models
2.2.1. RMSD Indicates Overall Stability of CLDN10a Dodecamer Models
2.2.2. Definition and Comparison of Interfaces within Dodecamer by Residue Contact Maps: cis- and ECS2-trans- Interfaces
2.2.3. Further Analysis of cis- and ECS2-trans- Interfaces in CLDN10a Dodecamers
2.2.4. Definition and Comparison of Interfaces within Dodecamer by Residue Contact Maps: ECS1 Loop Clusters
2.2.5. Further Analysis of β1β2 Loop Clusters
2.3. Ion Permeation Pathway of Pore in CLDN10a Dodecamer Models
2.4. Interaction of Pore-Lining Residues with Ions in CLDN10a and CLDN10b Channels
3. Discussion
4. Materials and Methods
4.1. Modeling and Simulation Platform
4.2. Modeling of CLDN10a IB Dodecamer Model
- i.
- Hydrophobic interface formed by the tip of β1β2 loops (V37 and I38)
- ii.
- Face-to-face (ftf) interface (C61-C61 H-bonds)
- iii.
- Linear-cis interface, where F68 (ECH) resides inside the pocket formed by F144, F145 and L156 (ECS2), and
- iv.
- Hydrophilic interaction between E155 (ECS2) and the backbone or side chain of ECH region residues T66 and I67 are formed.
- v.
- The CLDN10a-specific, positively charged residues R33 and K69 are oriented towards the anion-selective pore.
4.3. MD Simulations of CLDN10a IB Dodecamer Models
- i.
- IB-2—same constraints as IB-1: Force constant of 1 kcal mol−1 Å−2 on C61 backbone, all other atoms free.
- ii.
- IB-2+lic– additional 1 kcal mol−1 Å−2 on backbone atoms and β-carbon of I67 and F68 to weakly constrain linear cis-interface (lic),
- iii.
- IB-2+hc—additional 1 kcal mol−1 Å−2 on backbone atoms of helices to constrain mainly the transmembrane segments,
- iv.
- IB-2+ohc—additional 1 kcal mol−1 Å−2 on backbone atoms of helices of the outer chains, i.e., chains that are not part of the middle pore.
4.4. Analysis of the MD Trajectories
4.5. Applied Electric Field Simulations
4.6. Calculation of Ion Total Displacement
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Günzel, D.; Fromm, M. Claudins and other tight junction proteins. Compr. Physiol. 2012, 2, 1819–1852. [Google Scholar] [CrossRef] [PubMed]
- Günzel, D.; Yu, A.S.L. Claudins and the modulation of tight junction permeability. Physiol. Rev. 2013, 93, 525–569. [Google Scholar] [CrossRef]
- Otani, T.; Nguyen, T.P.; Tokuda, S.; Sugihara, K.; Sugawara, T.; Furuse, K.; Miura, T.; Ebnet, K.; Furuse, M. Claudins and JAM-A coordinately regulate tight junction formation and epithelial polarity. J. Cell Biol. 2019, 218, 3372–3396. [Google Scholar] [CrossRef] [PubMed]
- Piontek, J.; Krug, S.M.; Protze, J.; Krause, G.; Fromm, M. Molecular architecture and assembly of the tight junction backbone. Biochim. Biophys. Acta Biomembr. 2020, 1862, 183279. [Google Scholar] [CrossRef]
- Meoli, L.; Günzel, D. The role of claudins in homeostasis. Nat. Rev. Nephrol. 2023, 19, 587–603. [Google Scholar] [CrossRef]
- Weber, C.R.; Liang, G.H.; Wang, Y.; Das, S.; Shen, L.; Yu, A.S.L.; Nelson, D.J.; Turner, J.R. Claudin-2-dependent paracellular channels are dynamically gated. eLife 2015, 4, e09906. [Google Scholar] [CrossRef]
- Krause, G.; Winkler, L.; Mueller, S.L.; Haseloff, R.F.; Piontek, J.; Blasig, I.E. Structure and function of claudins. Biochim. Biophys. Acta 2008, 1778, 631–645. [Google Scholar] [CrossRef] [PubMed]
- Piontek, J.; Winkler, L.; Wolburg, H.; Müller, S.L.; Zuleger, N.; Piehl, C.; Wiesner, B.; Krause, G.; Blasig, I.E. Formation of tight junction: Determinants of homophilic interaction between classic claudins. FASEB J. Off. Publ. Fed. Am. Soc. Exp. Biol. 2008, 22, 146–158. [Google Scholar] [CrossRef]
- Suzuki, H.; Nishizawa, T.; Tani, K.; Yamazaki, Y.; Tamura, A.; Ishitani, R.; Dohmae, N.; Tsukita, S.; Nureki, O.; Fujiyoshi, Y. Crystal structure of a claudin provides insight into the architecture of tight junctions. Science 2014, 344, 304–307. [Google Scholar] [CrossRef]
- Suzuki, H.; Tani, K.; Tamura, A.; Tsukita, S.; Fujiyoshi, Y. Model for the architecture of claudin-based paracellular ion channels through tight junctions. J. Mol. Biol. 2015, 427, 291–297. [Google Scholar] [CrossRef]
- Nakamura, S.; Irie, K.; Tanaka, H.; Nishikawa, K.; Suzuki, H.; Saitoh, Y.; Tamura, A.; Tsukita, S.; Fujiyoshi, Y. Morphologic determinant of tight junctions revealed by claudin-3 structures. Nat. Commun. 2019, 10, 816. [Google Scholar] [CrossRef]
- Hempel, C.; Protze, J.; Altun, E.; Riebe, B.; Piontek, A.; Fromm, A.; Lee, I.M.; Saleh, T.; Günzel, D.; Krause, G.; et al. Assembly of Tight Junction Strands: Claudin-10b and Claudin-3 Form Homo-Tetrameric Building Blocks that Polymerise in a Channel-Independent Manner. J. Mol. Biol. 2020, 432, 2405–2427. [Google Scholar] [CrossRef]
- Gonschior, H.; Schmied, C.; Van der Veen, R.E.; Eichhorst, J.; Himmerkus, N.; Piontek, J.; Günzel, D.; Bleich, M.; Furuse, M.; Haucke, V.; et al. Nanoscale segregation of channel and barrier claudins enables paracellular ion flux. Nat. Commun. 2022, 13, 4985. [Google Scholar] [CrossRef]
- Milatz, S.; Himmerkus, N.; Wulfmeyer, V.C.; Drewell, H.; Mutig, K.; Hou, J.; Breiderhoff, T.; Muller, D.; Fromm, M.; Bleich, M.; et al. Mosaic expression of claudins in thick ascending limbs of Henle results in spatial separation of paracellular Na+ and Mg2+ transport. Proc. Natl. Acad. Sci. USA 2017, 114, E219–E227. [Google Scholar] [CrossRef]
- Nagarajan, S.K.; Klein, S.; Fadakar, B.S.; Piontek, J. Claudin-10b cation channels in tight junction strands: Octameric-interlocked pore barrels constitute paracellular channels with low water permeability. Comput. Struct. Biotechnol. J. 2023, 21, 1711–1727. [Google Scholar] [CrossRef]
- Daugherty, B.L.; Ward, C.; Smith, T.; Ritzenthaler, J.D.; Koval, M. Regulation of heterotypic claudin compatibility. J. Biol. Chem. 2007, 282, 30005–30013. [Google Scholar] [CrossRef]
- Furuse, M.; Sasaki, H.; Tsukita, S. Manner of interaction of heterogeneous claudin species within and between tight junction strands. J. Cell Biol. 1999, 147, 891–903. [Google Scholar] [CrossRef]
- Irudayanathan, F.J.; Wang, N.; Wang, X.; Nangia, S. Architecture of the paracellular channels formed by claudins of the blood-brain barrier tight junctions. Ann. N. Y. Acad. Sci. 2017, 1405, 131–146. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Krystofiak, E.S.; Ballesteros, A.; Cui, R.; Van Itallie, C.M.; Anderson, J.M.; Fenollar-Ferrer, C.; Kachar, B. Multiple claudin-claudin cis interfaces are required for tight junction strand formation and inherent flexibility. Commun. Biol. 2018, 1, 50. [Google Scholar] [CrossRef] [PubMed]
- Rajagopal, N.; Nangia, S. Unique structural features of claudin-5 and claudin-15 lead to functionally distinct tight junction strand architecture. Ann. N. Y. Acad. Sci. 2022, 1517, 225–233. [Google Scholar] [CrossRef]
- Berselli, A.; Alberini, G.; Benfenati, F.; Maragliano, L. Computational study of ion permeation through claudin-4 paracellular channels. Ann. N. Y. Acad. Sci. 2022, 1516, 162–174. [Google Scholar] [CrossRef]
- Berselli, A.; Alberini, G.; Benfenati, F.; Maragliano, L. Computational Assessment of Different Structural Models for Claudin-5 Complexes in Blood-Brain Barrier Tight Junctions. ACS Chem. Neurosci. 2022, 13, 2140–2153. [Google Scholar] [CrossRef]
- Berselli, A.; Benfenati, F.; Maragliano, L.; Alberini, G. Multiscale modelling of claudin-based assemblies: A magnifying glass for novel structures of biological interfaces. Comput. Struct. Biotechnol. J. 2022, 20, 5984–6010. [Google Scholar] [CrossRef]
- Milatz, S.; Piontek, J.; Schulzke, J.D.; Blasig, I.E.; Fromm, M.; Günzel, D. Probing the cis-arrangement of prototype tight junction proteins claudin-1 and claudin-3. Biochem. J. 2015, 468, 449–458. [Google Scholar] [CrossRef]
- Alberini, G.; Benfenati, F.; Maragliano, L. A refined model of claudin-15 tight junction paracellular architecture by molecular dynamics simulations. PLoS ONE 2017, 12, e0184190. [Google Scholar] [CrossRef]
- Samanta, P.; Wang, Y.; Fuladi, S.; Zou, J.; Li, Y.; Shen, L.; Weber, C.; Khalili-Araghi, F. Molecular determination of claudin-15 organization and channel selectivity. J. Gen. Physiol. 2018, 150, 949–968. [Google Scholar] [CrossRef]
- Fuladi, S.; McGuinness, S.; Shen, L.; Weber, C.R.; Khalili-Araghi, F. Molecular mechanism of claudin-15 strand flexibility: A computational study. J. Gen. Physiol. 2022, 154, e202213116. [Google Scholar] [CrossRef]
- Irudayanathan, F.J.; Wang, X.; Wang, N.; Willsey, S.R.; Seddon, I.A.; Nangia, S. Self-Assembly Simulations of Classic Claudins-Insights into the Pore Structure, Selectivity, and Higher Order Complexes. J. Phys. Chem. B 2018, 122, 7463–7474. [Google Scholar] [CrossRef]
- Raya-Sandino, A.; Lozada-Soto, K.M.; Rajagopal, N.; Garcia-Hernandez, V.; Luissint, A.C.; Brazil, J.C.; Cui, G.; Koval, M.; Parkos, C.A.; Nangia, S.; et al. Claudin-23 reshapes epithelial tight junction architecture to regulate barrier function. Nat. Commun. 2023, 14, 6214. [Google Scholar] [CrossRef] [PubMed]
- Furuse, M.; Nakatsu, D.; Hempstock, W.; Sugioka, S.; Ishizuka, N.; Furuse, K.; Sugawara, T.; Fukazawa, Y.; Hayashi, H. Reconstitution of functional tight junctions with individual claudin subtypes in epithelial cells. Cell Struct. Funct. 2023, 48, 1–17. [Google Scholar] [CrossRef]
- Colegio, O.R.; Van Itallie, C.M.; McCrea, H.J.; Rahner, C.; Anderson, J.M. Claudins create charge-selective channels in the paracellular pathway between epithelial cells. Am. J. Physiol. Cell Physiol. 2002, 283, 142–147. [Google Scholar] [CrossRef]
- Hashimoto, Y.; Poirier, K.; Boddaert, N.; Hubert, L.; Aubart, M.; Kaminska, A.; Alison, M.; Desguerre, I.; Munnich, A.; Campbell, M. Recurrent de novo mutations in CLDN5 induce an anion-selective blood-brain barrier and alternating hemiplegia. Brain 2022, 145, 3374–3382. [Google Scholar] [CrossRef]
- Berselli, A.; Alberini, G.; Benfenati, F.; Maragliano, L. The impact of pathogenic and artificial mutations on Claudin-5 selectivity from molecular dynamics simulations. Comput. Struct. Biotechnol. J. 2023, 21, 2640–2653. [Google Scholar] [CrossRef]
- Nitta, T.; Hata, M.; Gotoh, S.; Seo, Y.; Sasaki, H.; Hashimoto, N.; Furuse, M.; Tsukita, S. Size-selective loosening of the blood-brain barrier in claudin-5-deficient mice. J. Cell Biol. 2003, 161, 653–660. [Google Scholar] [CrossRef]
- Günzel, D.; Stuiver, M.; Kausalya, P.J.; Haisch, L.; Krug, S.M.; Rosenthal, R.; Meij, I.C.; Hunziker, W.; Fromm, M.; Müller, D. Claudin-10 exists in six alternatively spliced isoforms that exhibit distinct localization and function. J. Cell Sci. 2009, 122, 1507–1517. [Google Scholar] [CrossRef]
- Van Itallie, C.M.; Rogan, S.; Yu, A.; Vidal, L.S.; Holmes, J.; Anderson, J.M. Two splice variants of claudin-10 in the kidney create paracellular pores with different ion selectivities. Am. J. Physiol. Ren. Physiol. 2006, 291, F1288–F1299. [Google Scholar] [CrossRef]
- Curry, J.N.; Tokuda, S.; McAnulty, P.; Yu, A.S.L. Combinatorial expression of claudins in the proximal renal tubule and its functional consequences. Am. J. Physiol. Ren. Physiol. 2020, 318, F1138–F1146. [Google Scholar] [CrossRef]
- Milatz, S.; Piontek, J.; Hempel, C.; Meoli, L.; Grohe, C.; Fromm, A.; Lee, I.M.; El-Athman, R.; Günzel, D. Tight junction strand formation by claudin-10 isoforms and claudin-10a/-10b chimeras. Ann. N. Y. Acad. Sci. 2017, 1405, 102–115. [Google Scholar] [CrossRef]
- Hempel, C.; Rosenthal, R.; Fromm, A.; Krug, S.M.; Fromm, M.; Günzel, D.; Piontek, J. Tight junction channels claudin-10b and claudin-15: Functional mapping of pore-lining residues. Ann. N. Y. Acad. Sci. 2022, 1515, 129–142. [Google Scholar] [CrossRef]
- Krug, S.M.; Günzel, D.; Conrad, M.P.; Lee, I.F.; Amasheh, S.; Fromm, M.; Yu, A.S. Charge-selective claudin channels. Ann. N. Y. Acad. Sci. 2012, 1257, 20–28. [Google Scholar] [CrossRef]
- Jo, S.; Vargyas, M.; Vasko-Szedlar, J.; Roux, B.; Im, W. PBEQ-Solver for online visualization of electrostatic potential of biomolecules. Nucleic Acids Res. 2008, 36, W270–W275. [Google Scholar] [CrossRef]
- Li, J.; Zhuo, M.; Pei, L.; Rajagopal, M.; Yu, A.S. Comprehensive cysteine-scanning mutagenesis reveals Claudin-2 pore-lining residues with different intrapore locations. J. Biol. Chem. 2014, 289, 6475–6484. [Google Scholar] [CrossRef]
- Alberini, G.; Benfenati, F.; Maragliano, L. Molecular Dynamics Simulations of Ion Selectivity in a Claudin-15 Paracellular Channel. J. Phys. Chem. B 2018, 122, 10783–10792. [Google Scholar] [CrossRef]
- Conrad, M.P.; Piontek, J.; Günzel, D.; Fromm, M.; Krug, S.M. Molecular basis of claudin-17 anion selectivity. Cell. Mol. Life Sci. CMLS 2016, 73, 185–200. [Google Scholar] [CrossRef]
- Piontek, A.; Rossa, J.; Protze, J.; Wolburg, H.; Hempel, C.; Günzel, D.; Krause, G.; Piontek, J. Polar and charged extracellular residues conserved among barrier-forming claudins contribute to tight junction strand formation. Ann. N. Y. Acad. Sci. 2017, 1397, 143–156. [Google Scholar] [CrossRef]
- Angelow, S.; Yu, A.S. Structure-function studies of claudin extracellular domains by cysteine-scanning mutagenesis. J. Biol. Chem. 2009, 284, 29205–29217. [Google Scholar] [CrossRef]
- Erramilli, S.K.; Dominik, P.K.; Ogbu, C.P.; Kossiakoff, A.A.; Vecchio, A.J. Cryo-EM structures of a synthetic antibody against 22 kDa claudin-4 reveal its complex with Clostridium perfringens enterotoxin. bioRxiv 2023. [Google Scholar] [CrossRef]
- Nusrat, A.; Parkos, C.A.; Verkade, P.; Foley, C.S.; Liang, T.W.; Innis-Whitehouse, W.; Eastburn, K.K.; Madara, J.L. Tight junctions are membrane microdomains. J. Cell Sci. 2000, 113 Pt 10, 1771–1781. [Google Scholar] [CrossRef]
- Ikenouchi, J. Roles of membrane lipids in the organization of epithelial cells: Old and new problems. Tissue Barriers 2018, 6, 1–8. [Google Scholar] [CrossRef]
- Shigetomi, K.; Ono, Y.; Inai, T.; Ikenouchi, J. Adherens junctions influence tight junction formation via changes in membrane lipid composition. J. Cell Biol. 2018, 217, 2373–2381. [Google Scholar] [CrossRef]
- Khalili-Araghi, F.; Ziervogel, B.; Gumbart, J.C.; Roux, B. Molecular dynamics simulations of membrane proteins under asymmetric ionic concentrations. J. Gen. Physiol. 2013, 142, 465–475. [Google Scholar] [CrossRef] [PubMed]
- Irudayanathan, F.J.; Nangia, S. Paracellular Gatekeeping: What Does It Take for an Ion to Pass Through a Tight Junction Pore? Langmuir 2020, 36, 6757–6764. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.L.; Li, J.; Zhang, J.; Zeng, B. To Be or Not to Be an Ion Channel: Cryo-EM Structures Have a Say. Cells 2023, 12. [Google Scholar] [CrossRef]
- Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Zidek, A.; Potapenko, A.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. [Google Scholar] [CrossRef]
- Mirdita, M.; Schutze, K.; Moriwaki, Y.; Heo, L.; Ovchinnikov, S.; Steinegger, M. ColabFold: Making protein folding accessible to all. Nat. Methods 2022, 19, 679–682. [Google Scholar] [CrossRef]
- Polak, E.; Ribiere, G. Note on Convergence of Conjugate Direction Methods. Rev. Fr. Inform. Rech. Oper. 1969, 3, 35–43. [Google Scholar]
- Bowers, K.J.; Chow, E.; Xu, H.; Dror, R.O.; Eastwood, M.P.; Gregersen, B.A.; Klepeis, J.L.; Kolossváry, I.; Moraes, M.A.; Sacerdoti, F.D.; et al. Scalable Algorithms for Molecular Dynamics Simulations on Commodity Clusters. In Proceedings of the SC’06: 2006 ACM/IEEE Conference on Supercomputing, Tampa, FL, USA, 11–17 November 2006; p. 43. [Google Scholar]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Lu, C.; Wu, C.; Ghoreishi, D.; Chen, W.; Wang, L.; Damm, W.; Ross, G.A.; Dahlgren, M.K.; Russell, E.; Von Bargen, C.D.; et al. OPLS4: Improving Force Field Accuracy on Challenging Regimes of Chemical Space. J. Chem. Theory Comput. 2021, 17, 4291–4300. [Google Scholar] [CrossRef]
- Martyna, G.J.; Klein, M.L.; Tuckerman, M.E. Nosé-Hoover chains: The canonical ensemble via continuous dynamics. J. Chem. Phys. 1992, 97, 2635–2643. [Google Scholar] [CrossRef]
- Martyna, G.J.; Tobias, D.J.; Klein, M.L. Constant pressure molecular dynamics algorithms. J. Chem. Phys. 1994, 101, 4177–4189. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Michaud-Agrawal, N.; Denning, E.J.; Woolf, T.B.; Beckstein, O. MDAnalysis: A toolkit for the analysis of molecular dynamics simulations. J. Comput. Chem. 2011, 32, 2319–2327. [Google Scholar] [CrossRef]
- Gowers, R.J.; Linke, M.; Barnoud, J.; Reddy, T.; Melo, M.N.; Seyler, S.L.; Domanski, J.J.; Dotson, D.L.; Buchoux, S.; Kenney, I.M.; et al. MDAnalysis: A Python Package for the Rapid Analysis of Molecular Dynamics Simulations. In Proceedings of the 15th Python in Science Conference, Austin, TX, USA, 11–17 July 2016; pp. 98–105. [Google Scholar] [CrossRef]
- Rossum, G.v.; Drake, F.L. Python 3 Reference Manual. CreateSpace: Scotts Valley, CA, USA, 2009. [Google Scholar]
- Smart, O.S.; Goodfellow, J.M.; Wallace, B.A. The pore dimensions of gramicidin A. Biophys. J. 1993, 65, 2455–2460. [Google Scholar] [CrossRef]
- Smart, O.S.; Neduvelil, J.G.; Wang, X.; Wallace, B.A.; Sansom, M.S. HOLE: A program for the analysis of the pore dimensions of ion channel structural models. J. Mol. Graph. 1996, 14, 354–360. [Google Scholar] [CrossRef]








| Parameter | CLDN10a (IB-2) | CLDN10b |
|---|---|---|
| Architecture | interlocked pore barrels, JDR; (Figure 1) | interlocked pore barrels, JDR; (Figure 1) [15] |
| RMSD (dodecamer) | ~1.7 Å; (Figure S4A) | 1.5–2.2 Å; Figure S4A |
| Linear-cis interface | maintained, non α-helical ECH region, F68 in, I67 close to ECS2 pocket; (Figure 2 and Figure 3) | maintained, α-helical ECH region, M69 but not L70 in ECS2 pocket |
| Face-to-face interface | maintained; (Figure 2 and Figure 3) | maintained; [15] |
| ECS2-ECS2-trans interface | contact maintained, flexible; (Figure 3),F144, F145 close to P147; (Figure 2) | contact maintained, flexible; [15]; F146, F147 close to P149, P149 close to P149; (Figure 2), [15] |
| β1β2loop tip cluster: V37/39,I39/I40 proximities | trans < 4 Å, cis < 5 Å; (Figure 4) | trans <3 Å, cis <3 Å; (Figure 4), [15] |
| β1β2loop tip cluster: V37/39,I39/I40 SASA | 74- 117 Å2; (Figure 5) | 49-70 Å2; [15] |
| Minimal pore diameter | ~5.1 Å; (Figure 6) | ~5.2 Å; [15] |
| Pore center lined by Bold: frequent ion contact | 4× N54, 4× H60 (Ø ~6.7 Å); (Figure 6) | 4× D56, 4× N62 (also narrowest site); [15] |
| Charged residues (pore center to periphery) Bold: frequent ion contact | R62, R33, (E155), K69, E151, K29, E143, D146, K139; (Figure 6) | K64, D36, (E157), E153, K31, E145, D148, D73, K141; [15] |
| Other pore-lining residues | Polar: Q45, N50, S58, H64 | Nonpolar: A47, A52, V60, F66 |
| Pore net charge | +8 | −12 |
| Electrostatic surface potential of pore | mainly positive; (Figure 7) | mainly negative; (Figure 7) |
| Charge selectivity of channel | Strong anion attraction, anion conductance; (Figure 7 and Figure 8) | Strong cation attraction, cation conductance; (Figure 7 and Figure 8) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nagarajan, S.K.; Piontek, J. Molecular Dynamics Simulations of Claudin-10a and -10b Ion Channels: With Similar Architecture, Different Pore Linings Determine the Opposite Charge Selectivity. Int. J. Mol. Sci. 2024, 25, 3161. https://doi.org/10.3390/ijms25063161
Nagarajan SK, Piontek J. Molecular Dynamics Simulations of Claudin-10a and -10b Ion Channels: With Similar Architecture, Different Pore Linings Determine the Opposite Charge Selectivity. International Journal of Molecular Sciences. 2024; 25(6):3161. https://doi.org/10.3390/ijms25063161
Chicago/Turabian StyleNagarajan, Santhosh Kumar, and Jörg Piontek. 2024. "Molecular Dynamics Simulations of Claudin-10a and -10b Ion Channels: With Similar Architecture, Different Pore Linings Determine the Opposite Charge Selectivity" International Journal of Molecular Sciences 25, no. 6: 3161. https://doi.org/10.3390/ijms25063161
APA StyleNagarajan, S. K., & Piontek, J. (2024). Molecular Dynamics Simulations of Claudin-10a and -10b Ion Channels: With Similar Architecture, Different Pore Linings Determine the Opposite Charge Selectivity. International Journal of Molecular Sciences, 25(6), 3161. https://doi.org/10.3390/ijms25063161