Class Separation Improvements in Pixel Classification Using Colour Injection

Abstract

This paper presents an improvement in the colour image segmentation in the Hue Saturation (HS) sub-space. The authors propose to inject (add) a colour vector in the Red Green Blue (RGB) space to increase the class separation in the HS plane. The goal of the work is the development of an algorithm to obtain the optimal colour vector for injection that maximizes the separation between the classes in the HS plane. The chromatic Chrominace-1 Chrominance-2 sub-space (of the Luminance Chrominace-1 Chrominance-2 (YC₁C₂) space) is used to obtain the optimal vector to add. The proposal is applied on each frame of a colour image sequence in real-time. It has been tested in applications with reduced contrast between the colours of the background and the object, and particularly when the size of the object is very small in comparison with the size of the captured scene. Numerous tests have confirmed that this proposal improves the segmentation process, considerably reducing the effects of the variation of the light intensity of the scene. Several tests have been made in skin segmentation in applications for sign language recognition via computer vision, where an accurate segmentation of hands and face is required.

1. Introduction

In recent years, a significant amount of work has been published in the field of colour segmentation for Human Computer Interfaces (HCI). We would like to emphasize those related to the segmentation of the natural colour of skin. In this area, Phung et al. [1] proposed a skin segmentation method using a Bayesian classifier, obtaining satisfactory results for different colour spaces such as: RGB, Hue Saturation Value (HSV), Luminance blue-Chrominance red-Chrominance (YC_bC_r) and Commission Internationale de l'Éclairage’s Luminosity a-channel b-channel (CIE-Lab), even under adverse illumination conditions. Hsu et al. [2] suggested the detection of face skin considering a nonlinear subspace from the YC_bC_r space to partially compensate the luminosity variations.

The robustness of the segmentation against luminosity changes is one of the most desirable features in colour segmentation systems. For this reason, much work on this topic has been focused on minimizing the effects of illumination changes by using colour spaces where the luminance or intensity component can be easily isolated, thus providing chromatic constancy. The actual trend in applications with important time-varying-illumination changes is to use dynamic colour models that can adapt themselves to compensate for variations of the scene illumination. In this area, an extensive overview of previous investigations in the skin colour segmentation field is presented by Sigal et al. [3].

The most frequently used colour spaces in these types of applications are HSV [3,4] and normalized Red Green (rg) [5–7]. The HSV space, as well as the Hue Saturation Intensity (HSI) and Hue Lightness Saturation (HLS) spaces, are widely used in image processing because it is very intuitive for the human brain to interpret the information as it is represented. In some works, only the Hue (H) and Intensity (I) components are used in the clustering process [8]. In other cases, a threshold value for the Saturation (S) of each pixel based on its intensity is defined [9]. This threshold is used before the clustering process to determine if S should be replaced by H or I.

In general, all these segmentation proposals offer good results for objects with significant size in the scene or in cases where the main goal is object tracking, but not in the case of shape recognition. If the goal is to recognize the object shape, the system requirements are higher and very accurate segmentation techniques should be applied. Further difficulties may arise if the images have low quality and spatial resolution. Sign language recognition systems based on computer vision are a good example of these types of applications. In this case, the camera should capture all the upper parts of the speaker’s body, implying that the parts to segment (hands and face) constitute a small part of the captured scene. In this field, Habili et al. [10] performed a pixel-by-pixel classification of the skin colour with discriminant features of the C_bC_r plane, using the Mahalanobis distance, but they needed a fusion of motion cues to obtain good results. Similar skin segmentation is achieved in the work done by Chai et al. [11], where post-segmentation stages were applied, such as morphological operations, in order to surpass the limitations of the segmentation. The YC_bC_r space has been also used [11]. This colour space is one of the most widely used in the segmentation process.

In this field, Ribiero and Gonzana [12] presented hand segmentation in video sequences by means of the Gaussian Mixture Model (GMM) background subtraction algorithm, which is a well-known statistical model for density estimation due to its tractability and universal approximation capability. In this work, [12], an adaptive Gaussian mixture in time is used to model each pixel distribution in RGB space. In Huang and Liu’s work [13], clustering of colour images using GMM technique in HSV space is performed.

Less common colour spaces are also used in other works: both linear transformation spaces, like Luminance E-channel S-channel (YES) [14], and non-linear, spaces like the Uniform Chromaticity Scale (UCS) spaces, such as Luminance u-channel v-channel (L*u*v*) and its representation in cylindrical coordinates Intensity Hue Saturation (IHS) [15], Saturation Tint Value (STV) [16] which is a representation of HSV space by the normalized RGB components. Other spaces used are the Spherical Coordinate Transform (SCT) [17] and the geodesic chromaticity space pq [18].

We can also find works related to object/background segmentation with the objective of efficiently delimiting object edges. Some of these publications present the use of graph cuts in N-dimensional images to segment medical images from computed tomography (CT) scanners [19,20], and multilevel graph cuts to accelerate the segmentation and optimize memory use [21]. From our point of view, the main disadvantage of these works is that they are not designed for real-time purposes.

The conclusion of these previous works is that important unresolved problems still exist in order to obtain efficient skin segmentation, especially if we take into account that many applications require real time processing, include complex scenes, are prone to important illumination changes, and the objects to segment (face, arms and hands) are small when compared to the captured scene.

Our contribution to the solution of this segmentation problem is to use an object/background pre-processing technique to enhance the contrast (in the HS plane) between the colours corresponding to the objects to segment and the background in each frame. This pre-processing consists of increasing the separation between the object and background classes in the HS plane to optimize the segmentation in that plane.

In our proposal, to increase the class separation, a colour vector of components Δ_R, Δ_G, Δ_B, is added to the R, G and B images directly captured from the camera, modifying the value of each pixel (n) to (R_n+Δ_R, G_n+Δ_G, B_n+Δ_B). The objective of this paper is to present the process needed to obtain the values Δ_R, Δ_G and Δ_B that optimize the separation between the classes of interest once the image has been converted to the HS plane. This optimization is carried out by means of an algorithm that maximises the Fisher Ratio. We have called the colour vector addition process “colour injection”. In our proposal, the colour injection process is achieved using the relationships between the RGB, YC₁C₂ [8,22,23] and HSI [24–26] colour spaces, and the properties of the C₁C₂ plane.

Our system may be particularized to recognize sign language in real-time and special attention has been paid to the detection of the geometric form of the parts to segment, hands and face edges, in each frame. Our proposal has been thoroughly tested with very good results even with illumination variations, because it isolates the I component. We always attempt to work outside the instability or achromatic zone of the HS plane, due to the convenient redistribution in the HS plane of the existing classes in the colour injected image (seen in [15] for the IHS space). In order to perform a comparative qualitative study between the segmentations of the original images and the colour injected images (proposal presented in this paper), a GMM clustering technique in the HS classification domain is used. This technique has been used in a similar way for the HSV space [13]. In previous works, different formulations for the HSI space can be found [22,24–26]. We use the formulation proposed in [26].

This paper has been organized as follows: Section 2 describes the basis of the proposed algorithm to increment the separation between classes. Section 3 presents the criteria considered when separating the classes. Section 4 describes the off-line initialization stage of the proposed algorithm. Section 5 details how to improve the separation between classes in the HS plane starting from their location in the C₁C₂ plane. Section 6 presents the algorithm that performs the optimal class separation. Section 7 describes how to obtain the colour vector for injection, and its effects in the captured images. Section 8 contains the experimental results, and Section 9 provides the conclusions and future work.

2. Overview of the Colour Injection Algorithm

The objective of this work is to improve the segmentation process using colour injection. In order to do that, a colour vector for injection is obtained for each captured image in the RGB space. This colour vector is considered optimal, because it is calculated to maximize the separation between the classes to segment in the HS plane (subspace where the segmentation is performed). For this reason, this colour vector will be called optimal colour vector in this paper and will be denoted by i_r. It is injected in the RGB space and is calculated starting from significant samples (seeds) from the object to segment and from the part of the scene considered as background. The procedure to obtain the vector i_r, and the reason why it is optimal is explained in Sections 6 and 7. This optimal colour vector is given by:

$${\mathbf{i}}_{\mathbf{r}}={\left[{\Delta }_R {\Delta }_G {\Delta }_B\right]}^T$$

(1)

where Δ_R, Δ_G and Δ_B are the increments of the colour components R, G and B, respectively.

The optimal colour vector, i_r, is injected in every frame of an image sequence in real-time applications to segment objects in colour images. Its efficiency has been especially tested in applications where a reduced contrast between the background colour and the colour of the object to segment exists, when there are illumination changes and the size of the object to segment is very small in comparison with the size of the captured scene.

An important property of the perceptual colour spaces (such as the HSI space) is that they produce a maximum disconnection between the chrominance and luminance components. As a result, the luminance can be almost fully isolated, making the segmentation process more invariant to the changes in shades and illumination as in [4]. For this reason, the analysis of the colour injection effects in the HSI space is made only using the H and S chromatic components (HS plane).

As the segmentation is performed using the HS components, we try to separate the representative vectors of the two classes (object and background) in angle (H component) and in magnitude (S component) using colour injection. However, special attention should be paid in this separation process to the variations of the dispersions (reliability) of both classes after the colour injection, because it has a very high incidence in the class separation process.

In short, if the original image is denoted by I, the optimal colour vector to add by i_r, and the coloured image resulting of the colour injection by I_i, is fulfilled:

$${\mathrm{I}}_{\mathrm{i}}=\mathrm{I}+{\mathbf{i}}_{\mathbf{r}}$$

(2)

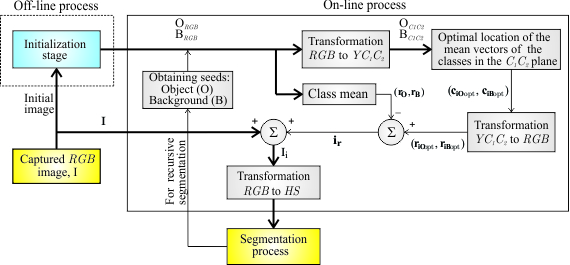
The algorithm proposed in this work is formed by two clearly different stages: an off-line and an on-line stage. The off-line stage is an initialization phase whose objective is to determine the optimal number of existing classes in the initial frame, and, from that, to obtain the object (O class) and background (B class) classes needed to carry out their separation. The off-line stage is explained in detail in Section 4. The result of this stage is the set of significant pixels (seeds) in the RGB space that represent both classes, identified by: O_RGB = {r_O1, r_O2… r_ON}, and B_RGB = {r_B1, r_B2… r_BM}, respectively, where r_Or for r = 1, 2… N and r_Bq for q = 1, 2… M refer to the pixel vectors of the object and background classes, respectively.

The on-line stage is the novel contribution of this paper. Its objective is to determine the optimal colour vector to inject (i_r) for each frame in order to increase, optimally, the separation between classes O and B. The on-line process is executed before the segmentation process for each frame captured in real time. Figure 1 depicts the different phases of a segmentation process that uses the colour injection proposal of this paper.

The on-line process consists of the following stages:

• For every O_RGB and B_RGB sample from the captured RGB image I, a transformation to the YC₁C₂ space is done. Considering the chromatic components after the transformation, the resulting classes will be referred to as O_C1C2 = {c_O1, c_O2… c_ON} for the object class and as B_C1C2 = {c_B1, c_B2… c_BM} for the background, where the pixel vectors are denoted by “c”.
• Using the properties of the C₁C₂ plane and the relationship between the HSI and YC₁C₂ colour spaces, the optimal location of the classes in the C₁C₂ space is obtained by finding the optimal location of their respective mean vectors. The optimal location is the one that maximizes the class separation in the HS plane (maximum distance between the class means and minimum class dispersions). These optimal mean vectors will be referred to as c_iOopt and c_iBopt. This phase is, undoubtedly, the most important of this work, and will be described in detail in subsequent sections.
• From the mean vectors c_iOopt and c_iBopt, their corresponding ones in the RGB space, r_iOopt and r_iBopt, are calculated.
• From the vectors r_iOopt and r_iBopt, and the mean vectors of the original classes (O_RGB, B_RGB) denoted by r_O and r_B, the optimal colour vector for injection is obtained. This optimal colour vector can be calculated from one of these expressions:

  $$\begin{array}{ccccc}{\mathbf{i}}_{\mathbf{r}}={\mathbf{r}}_{\mathbf{iO}\text{opt}}-{\mathbf{r}}_{\mathbf{O}},& & & & {\mathbf{i}}_{\mathbf{r}}={\mathbf{r}}_{\mathbf{iB}\text{opt}}-{\mathbf{r}}_{\mathbf{B}}\end{array}$$

  (3)
• Once the optimal colour vector has been obtained, the new “injected” image I_i can be calculated applying (2).

Finally, the coloured image I_i is transformed from the RGB space to the HS plane, where the segmentation is done, because the colour injection has its effects in the HSI space: the increase in the separation between the classes only happens in the HSI space or HS plane (in the RGB space the colour injection only produces a translation of the classes, keeping the distance between them constant, independently of the colour injection).

The proposed method can be implemented easily and can be used in real-time applications. In the following sections, the process to obtain the optimal vector for injection is presented in detail. At the end of this paper, in order to facilitate its reading, we have included three appendices with aspects related to the relationships between the RGB, the HSI and YC₁C₂ spaces (Appendix A), statistical analysis of vectors in the RGB space and its relationships with the components in the HSI space (Appendix B), as well as the invariants of the mean vectors in the C₁C₂ plane (Appendix C).

3. Criteria for the Separation between Classes

Since the objective of our work is to obtain a higher separation between the classes to facilitate the segmentation, it is necessary to define a measure of the efficiency of our proposal. The Fisher Ratio (FR) is frequently used to measure the efficiency in the class separability in classification systems [6,27,28]. This ratio quantifies simultaneously the inter-class separation and the internal dispersion (reliability) of the classes. For a two-class system, it is interesting to achieve a large distance metric between the class means and a minimum dispersion within each class (leading to a high FR). In this work, the FR is used as a pixel classification measurement index, using as discriminant features the H and S components of each pixel.

In a multi-class system, the generalized Fisher Ratio is expressed by [29]:

$$\mathit{FR}=\text{tr}\left(M_w^{-1}{M}_b\right)$$

(4)

where M_b is the inter-class (between class) covariance matrix and M_w is the internal (within class) dispersion matrix of the classes.

Equation (4) cannot be directly applied due to the circular form of the H component trajectory. There are two main reasons for this:

• For two-class systems (as our case is), M_b may not represent the real angular distance between the hue means of the classes (the maximum angular distance between two vectors is π radians, even if one of the vectors is in the first quadrant of the HS plane and the other one in the fourth one). These problems have already been studied, for example in [8].
• The second reason is the discontinuity of the hue component when it moves from 2π to 0 radians (cyclic property). This implies that M_w matrix does not represent the real hue variance of a class whose mean is close to 0 (2π). The reason is that some of the vectors would have small angles (close to 0), and some others would have very high ones (close to 2π), resulting in a wrong and high variance. The resulting H mean would also be wrong.

For the previous reasons, and supposing that the correlation between H and S is low, a particular FR has been defined. This FR is individually calculated for each component, and, as our space is bi-dimensional, is given by [29]:

$$\mathit{FR}={\mathit{FR}}_H+{\mathit{FR}}_S$$

(5)

where FR_H and FR_S represent the Fisher Ratio of the H and S components, respectively, and are given by:

$$\begin{array}{ccc}{\mathit{FR}}_H=\frac{{\theta }_h^2}{{\sigma }_{\mathit{HO}}^2+{\sigma }_{\mathit{HB}}^2},& & {\mathit{FR}}_S=\frac{{\left(S_O-S_B\right)}^2}{{\sigma }_{\mathit{SO}}^2+{\sigma }_{\mathit{SB}}^2}\end{array}$$

(6)

where S_O − S_B is the distance between the saturation means of both classes, σ_SO and σ_SB are the standard deviations of the saturation component for both classes, θ_h is the separation angle between the hue means of both classes, and σ_HO and σ_HB are the standard deviations of the H component.

In (6) θ_h ∈ [0, π] represents the real angular distance between the hue means, because θ_h = cos⁻¹(CC_OB). This avoids the aforementioned problem about the angular distance between the hue means of the mean vectors of both classes in the HS plane. CC_OB is the correlation coefficient between the two mean vectors of the RGB components that have generated the mean vectors in the HS plane (Equation C.11) (see Appendix C). In this work, we have performed approximations in the calculation of σ_HO and σ_HB in order to avoid the problem of the hue discontinuity. Thus, the approximation for σ_HO is: ${\sigma }_{\mathit{HO}}^2={\sigma }_{\mathrm{C}\mathit{Ho}}^2+{\sigma }_{\mathrm{S}\mathit{Ho}}^2$, where σ_CHo is the standard deviation of every cos(H_Or) for r = 1, 2… N and σ_SHo is the standard deviation of every sin(H_Or). σ_HB is calculated with a similar method.

4. Initialization Stage (Off-Line Process)

The first step of the off-line process is the capture of a first frame (initial image). The seed pixels that represent the classes O and B are obtained from this image, by means of any clustering technique used to identify the existing classes of the image, such as K-Means [30], GMM [13], etc. In this paper, the GMM technique is used (in the HS domain) because it provides highly reliable classes, and, as a final result, it also provides the mean vectors, the covariance matrixes and the a priori probabilities of the classes. The clustering by means of GMM uses the EM algorithm (Expectation Maximization) to obtain the optimal location and dispersion of a predefined image class number (K), projected in the HS plane. Therefore, a Gaussian model is assumed for each existing class, considering a uniform scene illumination. The GMM algorithm is applied several times, initializing it with different K values, in order to obtain the optimal number of existing classes in the image (K_opt). K_opt corresponds with the K that produces the smallest error in the log-probability function of the EM algorithm, indicating that it is the best fit between the K Gaussians and the existing classes. Figure 2b shows the K_opt Gaussians projected in the HS plane, fitted to the existing classes in the initial image of the example in Figure 2a. Finally, Figure 2c depicts the original image segmentation as a function of the different existing classes (Figure 2b).

Once the GMM algorithm has converged, the following step is to find out the localization of the object class (O) in the HS plane. This off-line process is carried out easily, because the approximate location of the object class (O) in the HS plane is known at the beginning of the off-line process, as a result of the colour calibration adjustments of the camera. This approximate geometric locus in the HS plane is given by the mean vector h_init. Taking that into account, the detection of the object class (O) is performed by simply selecting the class with the minimum Euclidean distance with h_init. We preferred the Euclidean distance over the Mahalanobis distance because the detection of the object class could be incorrect if h_init is close to a class with high dispersion, and this class is also close to the object class (O). The reason of this effect is the consideration of the class covariance in the Mahalanobis distance.

Once the object class is detected, the next step is to select the background class (B). The background is usually formed by several classes, identified by {B₁, B₂… B_Kopt−1}. Our objective is to select the B_k class that will be considered as representative of the background and that we will be identified simply by B. Among all the classes that form the background, we will select the B_k that:

$$\mathrm{B}=\text{arg} \underset{{\mathrm{B}}_{\mathrm{k}}}{\text{min}}\left(\frac{P_{\mathit{FR}\mathrm{k}}\left({\mathrm{B}}_{\mathrm{k}}\right)}{P_{B\mathrm{k}}^2\left({\mathrm{B}}_{\mathrm{k}}\right)}\right)$$

(7)

being P_FRk; k = 1, 2… (K_opt − 1) the Fisher Ratio probabilities between the class O and each B_k, defined by $P_{\mathit{FR}\mathrm{k}}=\left(\sqrt{{\mathit{FR}}_{\mathrm{k}}}/{\sum }_{\mathrm{k}=1}^{\text{Kopt}}\sqrt{{\mathit{FR}}_{\mathrm{k}}}\right)$ where FR_k is the Fisher Ratio described in Section 3, and P_Bk; k = 1, 2… (K_opt − 1) the a priori probabilities of each B_k class to be the background class (B) of the image (given by the GMM algorithm).

Once the classes O and B have been identified, the seed pixels that represent both classes are obtained through an initial segmentation process of both the object class (O) and the background class (B). In this initial segmentation, the pdf (probability density function) of both classes in the HS plane are considered as unimodal bidimensional Gaussians, defined by the parameters obtained by the GMM clustering. This segmentation is carried out by selecting the pixels with higher probability to belong to the corresponding Gaussian. This stage of pixel selection is performed by truncating each class pdf with a determined threshold. This threshold corresponds to a percentage of the maximum probability of the corresponding bidimensional pdf, P_o, for the class O, and P_b for the class B. The values of {P_o, P_b} ∈ [1, 0], have been experimentally set to P_o = 0.45 and P_b = 0.6, using the Receiver Operating Characteristic (ROC) curves obtained from the different tests performed with real images. In this case a ROC curve was obtained by each class (O and B), using a set of real images, without and with colour injection. The thresholds P_o and P_b correspond with the nearest values to the elbows of the ROC curves. As the pixel selection is carried out in the HS plane, it is necessary to truncate the pdf in the Intensity axis, in order to obtain pixel sets that reliably represent the classes O and B in the RGB space. The truncation of this unidimensional pdf is necessary because the H and I components are independent (Appendix A) (this is important when the clustering is carried out in the HS plane) and this generates correspondence problems when the pixels in RGB components are selected from its projections in the HS plane. In this second pdf truncation, the percentages selected of the maximum value of the pdf intensity of each class are P_fo for O, and P_fb for B. These percentages have been set to P_fo = 0.4 and P_fb = 0.5.

Once the previous process is completed, a random sampling is carried out, selecting N samples for the class O and M for the class B, in order to reduce the working space dimension. This is the method to obtain the sets O_RGB and B_RGB mentioned in Section 2.

5. Separation of the Classes in the HS Plane from Their Location in the C₁C₂ Plane

This section details the most important relationships between the statistical mean and variance of the classes in the C₁C₂ and HS planes. Also, the effect of adding the same vector (colour injection) to two vectors in RGB space on the projections of these vectors in the C₁C₂ and HS planes is analyzed. This information is used to define an algorithm to easily calculate the optimal vector to inject in order to obtain the maximum separation between classes in the HS plane using translations in the plane C₁C₂.

5.1. Relationships between the HS and C₁C₂ Planes

Given two vectors in the RGB space, r_O and r_B, the resulting projection vectors in the C₁C₂ plane, c_O and c_B, and in the HS plane, h_O and h_B, fulfil (see Appendix A):

$${\theta }_c={\theta }_h=\theta$$

(8)

$$\mathbf{\Vert }{\mathbf{c}}_{\mathbf{O}}\mathbf{\Vert }\ne \mathbf{\Vert }{\mathbf{h}}_{\mathbf{O}}\mathbf{\Vert },\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathbf{\Vert }{\mathbf{c}}_{\mathbf{B}}\mathbf{\Vert }\ne \mathbf{\Vert }{\mathbf{h}}_{\mathbf{B}}\mathbf{\Vert }$$

(9)

$${\mathbf{\Vert }{\mathbf{d}}_{\mathbf{c}}\mathbf{\Vert }}^2=g_1\left({\mathbf{c}}_{\mathbf{O}},{\mathbf{c}}_{\mathbf{B}},{\theta }_c\right)={\mathbf{\Vert }{\mathbf{c}}_{\mathbf{O}}\mathbf{\Vert }}^2+{\mathbf{\Vert }{\mathbf{c}}_{\mathbf{B}}\mathbf{\Vert }}^2-2\mathbf{\Vert }{\mathbf{c}}_{\mathbf{O}}\mathbf{\Vert }\mathbf{\Vert }{\mathbf{c}}_{\mathbf{B}}\mathbf{\Vert }\text{cos}{\theta }_c$$

(10)

$${\mathbf{\Vert }{\mathbf{d}}_{\mathbf{h}}\mathbf{\Vert }}^2=g_2\left({\mathbf{c}}_{\mathbf{O}},{\mathbf{c}}_{\mathbf{B}},{\theta }_h,I_O,I_B,f\left(H\right)\right)$$

(11)

where θ_c is the angle between c_O and c_B, θ_h the angle between h_O and h_B; d_c is the distance vector between c_O and c_B, d_h is the distance vector between h_O and h_B; and I_O, I_B are the intensity means of both classes, object and background, respectively, corresponding to the h_O and h_B vectors. f(H) is a weighting function that depends on the H component. f(H) ∈ [½, 1] (see Appendix B).

It is important to note that, since the C₁C₂ plane is linear, when adding a vector i_r (injected vector) to both r_O and r_B in the RGB space, the distance vector d_c = c_O − c_B in the C₁C₂ plane remains constant. These constant magnitude and orientation values (invariants of the d_c vector) are denoted by ‖d_c‖ and φ (see Appendix C). Therefore, colour injections in the C₁C₂ plane result in class translations, as in the RGB space. This effect can be achieved with a translation vector i_c (corresponding to i_r) directly added in the C₁C₂ plane.

Moreover, in the case of the C₁C₂ plane, (10) is verified (cosine law). Therefore, given that ‖d_c‖ remains constant for the different values of i_r, the values of θ, ‖c_O‖ and ‖c_B‖, will be modified as a function of the value of i_r. In the case of the HS plane, it must be said that if i_r is added to the vectors r_O and r_B (contrary to what happens in the C₁C₂ plane) the difference vector d_h also varies. The reason is that, according to (11), d_h depends on the value of I_O and I_B and on the f(H) weighting function. In any case (8) always holds.

In short, to calculate the value of the colour vector to be added in the RBG space to obtain a particular separation between the classes in the HS plane, the authors suggest using the relationships between the h vector components in the HS plane, and their corresponding c vector components in the C₁C₂ plane, given by (Equation B.12) and (Equation B.13) (see Appendix B), and the relationship between pairs of vectors in these planes, given by (8, 9, 10 and 11).

Therefore, the proposed algorithm is based on the analysis of the behaviour of the vectors c_O and c_B in the C₁C₂ plane and the properties of its difference vector d_c (‖d_c‖ and φ are invariant). These invariants allow us to establish a mathematical relationship between the class mean vectors before and after the colour injection. Thus, for example, the separation angle (hue difference) between two vectors in the HS plane can be easily controlled with the separation angle of the same vectors (c_O, c_B) in the C₁C₂ plane, because both angles coincide (8).

In Figure 3, an example of the correspondence between the vectors c_O and c_B in the C₁C₂ plane and the vectors h_O and h_B in the HS plane is shown. The relationships after performing the colour injection (vectors c_iO, c_iB and h_iO, h_iB) are also shown, as well as the difference vector d_c before and after the colour injection, where the invariance in magnitude and angle can be observed. From now on, the “i” or “i” subscript refers to “colour injection”.

Figure 3 depicts how the translation of the vector d_c has favoured the separation of the mean vectors of the classes in both components (H and S), because θ_i > θ, and (‖h_iO‖ − ‖h_iB‖) > (‖h_O‖ − ‖h_B‖). An increase in the separation between the vectors after the colour injection can be verified (θ_I > θ). However, the vector modules (saturation) decrease (‖h_iO‖ < ‖h_O‖, ‖h_iB‖ < ‖h_B‖), since there is an unavoidable compensation effect given by (10) (notice that for a fixed I, ‖h‖ = const‖c‖f(H)).

We could obtain a great number of class locations within the HS plane relocating d_c with i_c all over the C₁C₂ plane. The determination of the optimal location is not a trivial task. In order to obtain an optimal i_c, it is possible to apply learning techniques, such as fuzzy systems and neural networks, that take as parameters some functions derived from FR’s (6) and the invariants of the vector d_c.

In the following Section (5.2), an algorithm for the calculation of the optimal i_r (corresponding to optimal i_c), conditioned to ‖c_iO‖ = ‖c_iB‖, is explained.

5.2. Separation between the Hue Means (Angular Separation)

The separation between the hue means is given by the angular separation between the vectors h_iO and h_iB, which indicate the colour separation. Once the expression of the distance between h_iO and h_iB is obtained, ‖d_ih‖ (see Figure 3), an optimization process can be applied to it as a function of the RGB components of i_r in order to obtain the optimal i_r that produces the maximum separation needed. The problem when calculating the optimal colour vector is that it is not possible to obtain its analytical expression, mainly due to the discontinuities in the function of ‖d_ih‖ (11).

In order to solve the problem posed by the discontinuities of ‖d_ih‖ in the HS plane, the authors propose to use the C₁C₂ plane, where the distance function between the vectors c_iO and c_iB, (‖d_c‖) (10) does not present discontinuities, and, as well, remains constant in magnitude and direction for different injections of colour vectors.

The interrelationship (due to the invariants of the vector d_c and the relationships between the HS and C₁C₂ planes) between the angle (θ_i) that the vectors c_iO and c_iB form and their modules (10) should be taken into account to obtain the separation angle (hue difference) of two vectors in the HS plane. Therefore, the maximum separation angle between the vectors may imply (due to the compensation effect) a diminution of their modules, and, consequently, the saturation of both vectors. The saturation reduction of the vectors h_iO and h_iB implies that they become closer to the achromatic zone (the origin of the coordinates system), which means that the colours approximate to gray scale. The consequence of this phenomenon is the loss of discriminating power in the segmentation.

Therefore, the proposed algorithm has been parameterized as a function of the mentioned separation angle θ_i between the vectors c_iO and c_iB. In our case, the optimal angle θ_i is obtained from an observation function that measures the effectiveness of the class separation in different locations in the HS plane. This function will be described in paragraph f of Section 6.

When the angle of separation θ_i reaches a maximum, θ_i coincides with the angle whose bisector is a straight line p, which passes through the origin of coordinates and is perpendicular to the straight line, l, whose director vector is d_c (Figure 4).

Therefore, the vector for injection (i_r) that causes the maximum hue difference, causes the modules of both vectors c_iO and c_iB to become equal (‖c_iO‖ = ‖c_iB‖). It also causes the distance between the intersection point of the lines p and l and the extreme of each vector to be ‖d_c‖/2. Figure 4 illustrates an example of the location of the vectors c_O and c_B after the injection of the colour vector (c_iO and c_iB) with those imposed restrictions.

The authors have given more importance to the angular (H) separation, because increasing both H and S at the same time is not possible. The main reason is that H has a discrimination power higher than S. Besides, the H component is totally uncorrelated to the I component, which does not occur to the S component (see Appendix B). Parameterization only by θ_i implies that we can only control the separation between the hue means. The starting point to obtain the distance between the saturation means is mainly the location of the vectors c_iO and c_iB with respect to the saturation weighting function in the C₁C₂ plane. As can be observed, in this process there is no control on the S component, so its contribution on the class separation will depend on the modification of the statistics of this component with the variation of θ_i.

5.3. Separation between the Saturation Means (Saturation Difference)

In this section, an analysis of the behaviour of the separation between the saturation components of two vectors in the HS plane is performed. Given two vectors, for example h_iO and h_iB, in the HS plane, we analyze how the value of the saturation difference between both vectors S_O − S_B = ‖h_iO‖ − ‖h_iB‖ varies. In our case, as ‖c_iO‖ = ‖c_iB‖ = C_i, then the intensities (I_O, I_B) corresponding to both vectors h_iO and h_iB, and the value of the saturation weighting function f(H) of each one, are the parameters with significant effect in the value of S_O − S_B. The reason is that, according to (Equation B.11), the difference S_O − S_B will only have a non-zero value if I and f(H) of both vectors are different (notice that the saturation varies inversely with the intensity, and directly with f(H)). As an example, Figure 3 shows vectors h_iO and h_iB (overlapped to their respective vectors c_iO and c_iB), as well as the saturation weighting curve f(H). In the case of Figure 3, the colour injection is done supposing I_O = I_B, therefore, the weighting function f(H) is the only responsible for the difference in the module of the vectors h_iO and h_iB, that is, of the separation between the saturation means of both classes. As previously indicated, in our proposal there is no control of the S_O − S_B value, but its behaviour as a function of the colour injections performed, parameterized by θ_i, is known. According to this, it can be said that S_O − S_B is determined, as expressed in (12), by: (a) the intensities of the vectors h_iO and h_iB (I_O, I_B), and (b) the module and angle of d_c (the invariants) since these determine the location of the vectors h_iO and h_iB along the curve f(H) in the HS plane. In the case of Figure 3, where h_iO is located in the third lobe and h_iB in the second, it is fulfilled:

$$S_O-S_B=k_1\text{cot}\left({\theta }_i/2\right)+k_2$$

(12)

where:

$$\begin{array}{l}{k}_1=\Vert {\mathbf{d}}_{\mathbf{c}}\Vert \left(I_B \text{cos}\left(5\pi /6+\phi \right)+I_O \text{cos}\left(\pi /2+\phi \right)\right)/3I_O{I}_B\mathrm{\hspace{0.17em} }\text{and}\hfill \\ \mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }{k}_2=\Vert {\mathbf{d}}_{\mathbf{c}}\Vert \left(I_O \text{sin}\left(\pi /2+\phi \right)-I_B \text{sin}\left(5\pi /6+\phi \right)\right)/3I_O{I}_B.\hfill \end{array}$$

5.4. Analysis of the Class Dispersion

In order to obtain the optimal vector for injection, i_r, by means of the suitable election of θ_i, we should take into account not only the information given by the mean vectors c_O and c_B in the C₁C₂ plane, but also the dispersion of the distributions of both classes.

In this section we analyze the behaviour of the class dispersions in the HS plane, that is, how the hue and saturation dispersions are affected when the classes are translated in the C₁C₂ plane, as a result of the colour injection. A class separation measurement function will be defined to quantify the effectiveness of the colour injection. This analysis will be necessary to understand how the H and S dispersions are modified with the colour injection, in addition to the performance of the class separation measurement function.

5.4.1. Hue dispersion (Angular dispersion)

The hue dispersion is determined by the effects of the dispersion transformation when passing from the C₁C₂ plane to the HS plane. If R_o is the (2 × N) matrix formed by the N vectors of the O class: c_Or; r = 1, 2… N, before any translation, the parameters of the O class uncertainty ellipse, i.e., the hue dispersion invariants, are obtained from the covariance matrix of R_o, by:

$${\omega }_O={\text{tan}}^{-1}\left(C_{\mathit{2}\mathit{Ou}}/C_{\mathit{1}\mathit{Ou}}\right)$$

(13)

where ω_O is the angle formed by the semi-major axis of the class uncertainty ellipse with respect to the horizontal axis (C₁), and C_1Ou and C_2Ou are the eigenvector components corresponding to the highest eigenvalue (λ_Ou) of the covariance matrix. The semi-major and semi-minor uncertainty ellipse axes, u_O and l_O respectively, which represent the maximum and minimum variance, are given by:

$$u_O=\sqrt{{\lambda }_{\mathit{Ou}}},\mathrm{\hspace{0.17em} }{l}_O=\sqrt{{\lambda }_{\mathit{Ol}}}$$

(14)

where λ_Ol is the minor eigenvalue of the covariance matrix. From these dispersion invariants, it is possible to obtain the model for the hue dispersion. Therefore, our interest is to obtain a correspondence between the hue dispersions in the HS plane by means of the information offered by the angular dispersion in the C₁C₂ plane. Knowing that the variation of the angular dispersion in the C₁C₂ plane corresponds with the variation of the hue dispersion in the HS plane, and since the C₁C₂ plane is a Cartesian plane, the problem is posed in the polar coordinates, taking these two considerations into account:

• As previously indicated, in the C₁C₂ plane, the colour injections only produce translations of the classes and, therefore, variations of their mean vector modules (‖c_iO‖, ‖c_iB‖). This causes the modification of the angular dispersions of both classes, because they depend on C_i = ‖c_iO‖ = ‖c_iB‖ (distance between the dispersion centre and the origin of the C₁C₂ plane). These effects of the hue dispersion modification have been observed when performing translations of a class by adding Gaussian noise in the RGB space [22,31]. In conclusion, the angular dispersion increases when the magnitude of its respective mean vector decreases due to the increment of the separation angle θ_i, according to:

  $$C_i=\mathbf{\Vert }{\mathbf{d}}_{\mathbf{c}}\mathbf{\Vert }/2\text{sin}\left({\theta }_i/2\right)$$

  (15)
• The geometric forms of the class distributions are not predetermined, but they can vary since they depend on the samples randomly taken from the object and the background. The colour injections produce class translations in the C₁C₂ plane, implying that from the point of view of the HS plane, the dispersion also depends on the geometric form of the classes. The reason is that, for different translations of a class, different orientations between the axis of maximum and minimum dispersion (represented by their uncertainty ellipse in a C₁C₂ plane) with respect to the orientation of their mean vectors (c_iO or c_iB) are generated. Therefore, independently of the class mean vector module, a distance d_a exists that contributes to the angular deviation. This distance d_a depends only on the geometric form and orientation of the dispersion after each translation. Then, d_a, in this case for the O class, will depend on the values of ω_O, u_O and l_O given by (13) and (14). This d_a can be approximated by means of the distance between the centre of the uncertainty ellipse and the intersection point between two right lines: one is the tangent line to the ellipse which at the same time passes through the origin of plane, and the other line is perpendicular to the previous one and it crosses the centre of the ellipse. With d_a and (15) the angular deviation can be approximated by:

  $${\sigma }_{\mathit{iH}}={\text{sin}}^{-1}\left(d_a/C_i\right)$$

  (16)

As an example, in Figure 5 we depict the object class (O) before a translation, for the addition of a vector i_c in this C₁C₂ plane, or, for the injection of a vector i_r, directly to the classes in RGB components. Over the object class, its respective uncertainty ellipse is shown.

In Figure 5, we can observe that the semi-major axis of the ellipse is relatively aligned to the mean vector c_O of the class, causing the perception of the minimum angular dispersion of that class. It can also be observed that the module of this mean vector, c_O, before the injection is greater than the module of the vector after it has been injected, c_iO, which, therefore, is also perceived as a minor angular dispersion by this effect. We may conclude then, that the initial location of this class in the HS plane represents a very favourable case, since the angular deviation before the colour injection is small.

Nevertheless, for the background class (B) before the colour injection, certain alignment between the mean vector c_B and the axis of greater dispersion of this class can also be observed, implying a reduced angular deviation. However, the problem is that the module of the vector c_B is reduced and, therefore, the angular deviation increases. In this case, it can be observed in Figure 5 that after the colour injection, the angular dispersion of the class B_i is smaller, since the module c_iB is greater.

Figure 6 depicts another example, with the different class locations after four colour injections. The modifications of the angular deviations σ_iHO and σ_iHB of the object and background classes as a function of the orientation of their respective uncertainty ellipses and the modules of their respective mean vectors can be observed.

5.4.2. Saturation dispersion

The dispersion of the saturation component is not directly affected by the class translations (due to the colour injections) in the C₁C₂ plane, if all the class vectors have the same intensity. The reason is that the saturation is a linear function of the C₁ and C₂ components. The expression of the saturation for lobe 1 of f(H) is (Equation B.13) (see Appendix B):

$$S=\frac{C_{\mathit{1}}}{3I}+\frac{C_{\mathit{2}}}{\sqrt{3}I}$$

(17)

This characteristic of linearity in the C₁C₂ plane makes the deviation of the saturation (σ_S) constant, since the distance between vectors in the C₁C₂ plane remains constant, independent of the colour injection. Nevertheless, in the HS plane σ_S will be different for each lobe of f(H) but will stay constant within each lobe. Evidently, if the class vectors have different intensity, the dispersion of the saturation will not be constant for each location, not even within the lobes (there is a greater variation of σ_S when the dispersion of the intensity component is greater).

Figure 7 illustrates how the hue and saturation dispersions are modified for the four colour injections of Figure 6.

In this case, the locations of both classes are projected in an HS Cartesian plane. The magnitude of the H and S deviation can be appreciated by means of the projections of the corresponding uncertainty ellipses of both classes in the axes H and S. In Figure 7a we can observe a diminution of the H deviation and the increase of the S deviation when the angle θ_i between the classes decreases, because the modules of the mean vectors of both classes increase. It can also be observed how the S deviation of the O_i class, is modified more than the deviation of B_i, because the I dispersion of O_i is greater. Figure 7b shows the same example as Figure 7a, but with the intensities of the class vectors equal to its intensity mean, i.e., I_O1 = I_O2 = ... = I_ON = I_O, and I_B1 = I_B2 = … = I_BM = I_B, implying that σ_IO = σ_IB = 0. Then, we can see how the S deviation of O_i, remains constant for each colour injection.

However, our interest in this paragraph is to understand how the colour injections affect the saturation dispersion. This is the reason why in our algorithm the S deviations of both classes are obtained considering their original intensities.

6. Algorithm for the Optimal Location of the Mean Vectors of Both Classes in C₁C₂ Plane

This section presents the strategy used to obtain, in the C₁C₂ plane, the mean vectors that maximize the separation between the classes in the HS plane. This section constitutes the main stage in Figure 1: “Optimal location of the mean vectors of the classes in the C₁C₂ plane”. As shown in Figure 1, for each captured image, an algorithm to obtain the optimal location in the C₁C₂ plane of the mean vectors of both classes (object and background) is executed. From these optimal vectors, c_iOopt and c_iBopt, and once the transformation to the RGB space is performed (r_iOopt, r_iBopt), the optimal vector to inject, i_r, is obtained using (3).

The proposal to obtain these optimal vectors, c_iOopt and c_iBopt, consists of different phases, and its general block diagram is depicted in Figure 8.

As can be observed, the proposal includes an iterative algorithm to obtain a set of locations for the mean vectors of the classes (c_iO and c_iB) in the C₁C₂ plane. The location of each vector will be parameterized by the angle formed between both vectors, θ_i. Therefore, we try to obtain a set of θ_in (θ_i1, θ_i2…). Each of them will have associated a measurement index of separation between classes that we will identify by β_HSn (β_HS1, β_HS2 …). From the function β_HSn = f (θ_in), the value of θ_in that produces the maximum separation between classes is obtained, θ_in optimal: θ_opt.

The process begins obtaining the mean vectors of each class in C₁C₂ plane. These mean vectors will be,

$$\begin{array}{llll}{\mathbf{c}}_{\mathbf{O}}=\mathrm{E}\left\{{\mathbf{c}}_{\mathbf{O}\mathbf{1}},{\mathbf{c}}_{\mathbf{O}\mathbf{2}}\dots {\mathbf{c}}_{\mathbf{O}N}\right\},\hfill & & & {\mathbf{c}}_{\mathbf{B}}=\mathrm{E}\left\{{\mathbf{c}}_{\mathbf{B}\mathbf{1}},{\mathbf{c}}_{\mathbf{B}\mathbf{2}}\dots {\mathbf{c}}_{\mathbf{B}M}\right\}\hfill \end{array}$$

(18)

From the vectors c_O and c_B, its difference vector, d_c, is obtained. As previously indicated, the magnitude, ‖d_c‖, and angle, φ, of the vector d_c are invariant against translations in the C₁C₂ plane. Their values are given by equation (19):

$$\begin{array}{ccc}\Vert {\mathbf{d}}_{\mathbf{c}}\Vert ={\left(d_{C\mathit{1}}^2+d_{C\mathit{2}}^2\right)}^{1/2},& & \phi =\{\begin{array}{l}{\text{cos}}^{-1}\left(d_{C\mathit{1}}/\Vert {\mathbf{d}}_{\mathbf{c}}\Vert \right);d_{C\mathit{2}}\ge 0\hfill \\ 2\pi -{\text{cos}}^{-1}\left(d_{C\mathit{1}}/\Vert {\mathbf{d}}_{\mathbf{c}}\Vert \right);d_{C\mathit{2}}<0\hfill \end{array}\end{array}$$

(19)

where d_C1 = C_1O − C_1B and d_C2 = C_2O − C_2B, such that (C_1O, C_2O) and (C_1B, C_2B) are the components of the vectors c_O and c_B, respectively.

The iterative process consists of the following six steps:

(a) Forced location of the mean vectors in the C₁C₂ plane

The original vectors c_O and c_B are relocated (forced) in the C₁C₂ plane using the invariants (‖d_c‖, φ), obtaining the new vectors (c_Io and c_Ib). Each location of the vectors (c_Io and c_Ib) should fulfil the following geometric restriction: the straight line that passes through the origin of the C₁C₂ plane and is perpendicular to the vector d_c should intersect this last one in ‖d_c‖/2. As previously indicated, this implies that:

$${\mathrm{C}}_{\mathrm{i}}\mathrm{\hspace{0.17em} }=\mathrm{\hspace{0.17em} }\Vert {\mathbf{c}}_{\mathbf{iO}}\Vert \mathrm{\hspace{0.17em} }=\mathrm{\hspace{0.17em} }\Vert {\mathbf{c}}_{\mathbf{iB}}\Vert =\Vert {\mathbf{d}}_{\mathbf{c}}\Vert /\left(2\text{sin}\left({\theta }_{\mathrm{i}}/2\right)\right)$$

(20)

This θ_I is the parameter to vary in order to obtain the different locations of the vectors C_IO and C_IB, and, therefore, of the locations of the classes in the C₁C₂ plane.

The Cartesian components of these vectors (Figure 4), particularized for the vector C_IO, are given by:

$$\begin{array}{ccc}{C}_{\mathit{1}\mathit{iO}}=C_i\text{cos}\left(H_{\mathit{iO}}\right),& & C_{\mathit{2}\mathit{iO}}=C_i\text{sin}\left(H_{\mathit{iO}}\right)\end{array}$$

(21)

where h_IO is the angle of the vector that can be expressed by:

$$H_{\mathit{iO}}=\pi /2+\phi -{\theta }_i/2$$

(22)

Similar expressions can be obtained for C_IB.

The iterative algorithm is initialized with an θ_i equal to θ (θ is the angle formed by the vectors c_O and c_B). In each iteration (j) of the algorithm, the value of θ_i is increased: θ_i(j) = θ_i(j − 1) + Δθ.

We should also take into account that θ_i represents the hue distance between the mean vectors (H_IO and H_IB) of the classes in the HS plane. This indicates that a direct relationship exists between the class translations in the C₁C₂ plane and the hue separation distance between the class means in the HS plane.

(b) Verification of the validity for the locations of the C_IO and C_IB vectors

For each increase of θ_i, the validity of the locations of the vectors C_IO and C_IB is verified. In case they are valid, the value of θ_i is included in the set θ_in. The validity of C_IO and C_IB (validity of θ_i) is tested by checking if the components of the corresponding vectors in RGB space (R_IO, R_IB) fulfil the limitations imposed by this space, i.e., the values are in the range [0, 1], because they are normalized with respect to 255.

(c) Calculation of the class translation vector in the C₁C₂ plane

The translation vector i_c is obtained for each value of θ_in. This vector i_c is responsible for the class translations from its original position to the forced location defined by θ_in. The translation vector i_c in the C₁C₂ plane corresponds to the vector to inject i_r in the RGB space. This translation vector can be calculated from any of the following expressions:

$${\mathbf{i}}_{\mathbf{c}}={\mathbf{c}}_{\mathbf{iO}}-{\mathbf{c}}_{\mathbf{O}},\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }{\mathbf{i}}_{\mathbf{c}}={\mathbf{c}}_{\mathbf{iB}}-{\mathbf{c}}_{\mathbf{B}}$$

(23)

(d) Translation of the classes in the C₁C₂ plane

The class translations in the C₁C₂ plane are performed with the value of i_c that has been calculated. Therefore, each vector c belonging to the object and background classes are increased by i_c:

$$\begin{array}{cccccc}{\mathrm{O}}_{\mathit{iC}\mathit{1}C\mathit{2}}=\left\{{\mathbf{c}}_{\mathbf{O}r}+{\mathbf{i}}_{\mathbf{c}}\right\};& r=1,2\dots N,& & & {\mathrm{B}}_{\mathit{iC}\mathit{1}C\mathit{2}}=\left\{{\mathbf{c}}_{\mathbf{B}q}+{\mathbf{i}}_{\mathbf{c}}\right\};& q=1,2\dots M\end{array}$$

(24)

(e) Class transformation from the C₁C₂ plane to the HS

The classes in the HS plane (o_IhS and b_IhS) are obtained from the translated classes o_IC1C2 and b_IC1C2, using (Equation B.12), (Equation B.13) and (Equation B.14).

(f) Observation function: calculation of the class separation measurement index (β_HSn) in the HS plane

As the class separation observation function, a normalized measurement index has been defined (β_HS) from the FR described in (5). It has been normalized to obtain β_HSn = 1 when the class separation is maximum. To obtain the β_HSn corresponding with each θ_in, we consider the mean and the dispersion of H and S of the classes, according to (6). Therefore, two class separation measurement indexes as a function of θ_in have been defined, one for each component:

$$\begin{array}{cccccc}{\beta }_{\mathit{Hn}}=\left(\sqrt{{\mathit{FR}}_H}-1\right)/\sqrt{{\mathit{FR}}_H},& & & & & {\beta }_{\mathit{Sn}}=\left(\sqrt{{\mathit{FR}}_S}-1\right)/\sqrt{{\mathit{FR}}_S}\end{array}$$

(25)

The final class separation measurement index is given by:

$${\beta }_{\mathit{HSn}}=k_h {\beta }_{\mathit{Hn}}+(1-k_h ){\beta }_{\mathit{Sn}}$$

(26)

where k_h is a weighting factor between β_Hn and β_Sn. The value of k_h ∈ [0, 1] is chosen depending on the prominence we want to give H or S in the segmentation process. Taking into account that H has a greater discriminating power than S, k_h > ½ should be fixed.

This iterative process is repeated until the first non valid value of θ_in is generated, and the pairs (β_HSn, θ_in) are registered to obtain the function β_HSn = f(θ_in) afterwards.

Once the set of pairs (β_HSn, θ_in) is obtained, the θ_in that produces the maximum class separation measurement index is selected. A cubic interpolation is performed around that local maximum to obtain the maximum of the interpolation index, β_HSmax, and its associated angle, θ_opt. Finally, with this θ_opt, the c_iOopt and c_iBopt vectors are obtained using (20), (21) and (22).

As an example, Figure 9 shows the variation curves, as a function of θ_in/2, of the statistical data: deviations of hue (σ_iHO and σ_iHB), deviation of saturation (σ_iSO and σ_iSB), and difference between the saturation means ‖S_iO − S_iB‖ needed to obtain the different class separation measurement indexes (25).

7. Calculation of the Optimal Colour Vector to Add and the Effects that it Produces on the Images

The calculation of the optimal colour vector to add, i_r, is the goal of our proposal, because this vector changes the colours of the captured image in a suitable manner, so that the classes separate and, therefore, the object class can be more easily segmented.

Figure 10 shows the values of β_Hn, β_Sn and β_HSn obtained from the values of the statistical data depicted in Figure 9. The values of (θ_opt, β_HSmax) obtained by interpolation are also shown.

As depicted in the block diagram of Figure 1, once the vectors c_iOopt and c_iBopt, that represent the optimal location of the classes in the HS plane, are obtained, the vectors r_iOopt and r_iBopt can be calculated. Thus, for instance, for the object class, O: if C_1Oopt and C_2Oopt are the C₁ and C₂ components of the vector c_iOopt respectively, the vector r_iOopt in RGB space is obtained by:

$${\mathbf{r}}_{\mathbf{iO}\text{opt}}={\mathbf{Q}}^{-1}{\left[Y_{\mathit{iO}} C_{\mathit{1}O\text{opt}} C_{\mathit{2}O\text{opt}}\right]}^T$$

(27)

where Q is the transformation matrix (Equation A.2) and Y_iO is the intensity mean of the object class translated in the C₁C₂ plane. The i_r vector is obtained with this r_iOopt applying (3). Considering that the colour injection can be made without modifying the mean intensity of the class after the injection of i_r, Y_iO = I_O holds. Although it is possible to modify the saturation mean varying the intensity mean, in this case, we want the saturation mean to be only affected by the f(H) value and the Chroma component (C). Therefore, the vector to inject, i_r, should have zero mean (E{i_r} = 0). The fact that E{i_r} = 0 implies that the intensity mean of the original image (I) and the injected one (I_i) are equal.

The effect of injecting the vector i_r to the original image in the new image, I_i, is a greater concentration of the pixel colours around the mean colour of each one of the two classes. That is, the colour injection contributes to the histogram equalization of the captured image in the HS plane. This equalization has a concentration effect on each class, and, therefore, the injection of i_r contributes to approaching the class distributions to a Gaussian shape. As an example, Figure 11 shows the 2D histograms of image I (Figure 11a) and of the coloured image resulting from the colour injection I_i, (Figure 11b), for a particular case (Figure 12 images).

In these figures (11a and 11b), the equalization of the histogram produced by the effect of the colour injection can be clearly observed. The segmentation of both images is shown in Figure 12c and 12d respectively. In this example, K_opt = 4, the O class corresponds with the jacket and the B class with the wall.

The effect of the class separation between O and B classes can also be directly seen, analyzing the class locations before and after the colour injection in their histograms. Figure 13 shows the histograms corresponding to the sets O_HS and B_HS in (a), and the sets O_iHS and B_iHS in (b). A remarkable increase in the hue component separation can be observed in the histograms of Figure 13b due to the colour injection.

The rest of the image classes different from B, B_x ≠ B; x = 1, 2 … K_opt − 2, are also affected by the effects of the colour injection. In this sense, as the class selected as B is the closest to the class O that also has a high probability to be the image background (fulfils equation (7)), when the separation between the classes O and B increases, the classes B_x also increase their separation with the class O. However, the colour injection decreases the separation between the class O and those classes B_x (B′x; x = 1, 2 …) that are closer than B to the class O but that were not selected as class B because they had a lower a priori probability. The consequence is that these classes (B′x) can be considered as class O, producing false positives in the object pixel classification.

Another effect of the colour injection is the automatic compensation of the illumination changes. That is, due to the equalization and the separation of the classes O and B in the injected image, there is a minimization of the problems produced by the illumination changes. The reason is that the main colour component affected by the illumination changes is S, and, as previously explained, our algorithm gives more importance to the separation of the most discriminant component, H. Then, both classes, O and B, always keep a certain separation, independently of the parameter variation of both distributions, and mainly when the mean and variance of the S component vary due to changes in the luminous intensity.

Next, in Figure 14, three histograms are presented, for the original and the injected image. All of them have been obtained with the different mean luminous intensity of the image (I_m = E{I} = E{I_i}): (I_m1 = 0.70, I_m2 = 0.45 and I_m3 = 0.21). The illumination compensation effects mentioned above can be observed in this figure.

8. Experimental Results

A bank of real images from different scenes has been used in a first phase of the practical tests, in order to evaluate the effectiveness of the proposed method. Here, a Gaussian classifier has been used as a segmentation technique, supposing a unimodal Gaussian model for the respective object and background class-conditional pdfs, i.e., p(h_i|O_i) and p(h_i|B_i). Thus, p(h_i|O_i) = g(h_i; h_iO, Σ_iO) is given by:

$$p\left({\mathbf{h}}_{\mathbf{i}}|{\mathrm{O}}_{\mathrm{i}}\right)=\frac{1}{2\pi {\left|{\mathbf{\Sigma }}_{\mathbf{iO}}\right|}^{1/2}}\text{exp}\left\{-\frac{1}{2}{d}_m\right\};\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }{d}_m={\left({\mathbf{h}}_{\mathbf{i}}-{\mathbf{h}}_{\mathbf{iO}}\right)}^T{\mathbf{\Sigma }}_{\mathbf{iO}}^{-1}\left({\mathbf{h}}_{\mathbf{i}}-{\mathbf{h}}_{\mathbf{iO}}\right)$$

(28)

where h_i represents each pixel of the image I_i, and Σ_iO is the covariance matrix of the injected object class in the HS plane. The segmentation is performed by thresholding the pdf (28) with a T_h value. This threshold is obtained knowing that we want to segment the class O_i taking the background class B_i as reference, so, T_h corresponds to the value of pdf (28) when: $d_m=\frac{1}{2}{\left({\mathbf{h}}_{\mathbf{iB}}-{\mathbf{h}}_{\mathbf{iO}}\right)}^T{\left({\mathbf{\Sigma }}_{\mathbf{iO}}+{\mathbf{\Sigma }}_{\mathbf{iB}}\right)}^{-1}\left({\mathbf{h}}_{\mathbf{iB}}-{\mathbf{h}}_{\mathbf{iO}}\right)=\frac{1}{2}\text{tr}\left(M_w^{-1}{M}_b\right)$. Therefore, T_h is given by:

$$T_h=\frac{1}{2\pi {\left|{\mathbf{\Sigma }}_{\mathbf{iO}}\right|}^{1/2}}\text{exp}\left\{-\frac{1}{4}\text{tr}\left(M_w^{-1}{M}_b\right)\right\}$$

(29)

The problems derived from the cyclical nature of the hue in the segmentations have been solved via software, using the convention introduced by Zhang and Wang [8].

In the evaluation, the same number of samples (seeds) for the object class (O) and the background (B) has been taken, M = N, in order to ensure that the difference between their statistical data is for intrinsic reasons, and not for differences in the sample space dimension. In the tests, the following data have been used: samples number: M = N = 50. Other tests with a higher number of seeds (M = N = 100, 200, 400, 800 and 1,600) have also been carried out, providing similar qualitative results in all of them, but with an increase in the iterative process computational cost. The increase of θ used in the algorithm shown in Figure 8: Δθ = 5°, interpolation interval ΔΘ = ±3Δθ and the weighting factor k_h in (26) has been experimentally selected for each experiment, always fulfilling k_h ∈ [0.75, 0.97]. In this stage, the experimental results have been quantified by means of the FR defined in (5).

Table 1. FR results for 14 cases in this work.

Case	FR	FR (Injected)	%Increase
1	49.15	112.32	128.53
2	74.67	246.82	230.52
3	11.18	21.84	95.31
4	68.08	1,826.02	2,581.97
5	100.82	214.46	112.71
6	96.27	173.50	80.22
7	209.62	735.81	251.01
8	23.91	63.16	164.15
9	123.15	2,277.07	1,749.00
10	9.49	44.52	369.11
11	126.27	946.48	649.56
12	21.02	197.71	840.32
13	65.13	74.68	14.66
14	1.604	5.57	247.70

shows the values of FR for 14 cases of the bank of images used in the tests.

Fourteen examples of segmentation can be seen in Figure 15 (figures a, b, c, d, e, f, g, h, i, j, k, l, m and n) that correspond with the 14 cases of FR calculated in Table 1. Four images are shown in each column (from up to down): the upper image is the original one (I), the second one is the coloured image (I_i), the third one, the results of the segmentation of the original image (I segmentation), and the lower one, the results of the segmentation of the injected image (I_i segmentation). The segmented images show the object pixels in green colour. For the figures between Figure 15a and Figure 15m, the object class (O) is the skin, and for Figure 15n, the object class is a jacket.

As can be observed, our proposal to inject a colour vector allows the attainment of remarkable improvements in the segmentation process, even with a segmentation technique as studied and effective as the Gaussian classifier.

As a second phase of the experimental tests, and in order to quantify the improvement in the segmentation of the injected image with respect to the original image, an analysis, pixel by pixel, has been made, comparing with the manually segmented reference images for the 14 cases. The data generated in this analysis, without noise added, are shown in

Table 2. Comparative analysis of the segmentations for the 14 example images shown in Figure 15, without noise added.

Case	Reference pixels*	CDR (%)		FDR (%)		CR (%)		Angle (°)		ir vector			kh	K	Fisher Ratio
		I	Ii	I	Ii	I	Ii	θ	θi	[R	G	B]			FR	FRi
a	10,503	91	97	33	33	67	67	25	179	[−24	0	24]	0.97	5	23	39
b	18,340	94	97	22	10	78	90	32	116	[−23	4	18]	0.93	5	16	55
c	5,749	96	89	76	58	24	42	7	282	[−15	−4	19]	0.65	11	6	9
d	13,460	93	97	13	11	87	89	4	258	[−15	1	15]	0.65	5	6	84
e	10,097	84	97	26	10	74	90	23	246	[−26	−1	27]	0.87	5	47	157
f	12,666	97	97	47	24	53	76	56	179	[−4	−8	13]	0.9	7	15	122
g	13,775	98	91	28	13	72	87	18	171	[−31	14	16]	0.93	5	48	1,118
h	12,231	91	96	115	29	−15	71	14	158	[−21	6	15]	0.95	6	5	77
i	9,063	97	95	34	22	66	78	6	126	[−30	20	10]	0.93	5	11	139
j	12,497	89	97	100	55	0	45	20	167	[−13	2	10]	0.85	5	3	17
k	12,512	97	95	22	14	78	86	3	193	[−27	7	20]	0.95	5	19	176
l	23,102	69	94	59	17	41	83	17	23	[−39	44	−6]	0.87	10	5	24
m	20,176	99	96	31	12	69	88	26	56	[−16	15	1]	0.6	5	25	27
n	38,629	67	82	35	19	65	81	6	298	[−13	−19	33]	0.55	4	5	21
Average		90	94	46	23	54	77	18	175	[−21	6	15]	0.83	6	17	148

^*Segmented Object Reference Image, I original image, Ii injected image

. The performance of the segmentation has been measured taking into account the classification Correct Detection Rate (CDR) and False Detection Rate (FDR) and the total Classification Rate (CR). CDR is the percentage of object pixels correctly classified, FDR is the percentage of background pixels incorrectly classified and CR is the total percentage of correctly classified pixels. Table 2 also shows the number (K) of Gaussians used by the GMM algorithm, the FR obtained by the statistics given by GMM for both classes, as well as the k_h used for each image.

Table 3. Comparative analysis of the segmentations for the 14 example images shown in Figure 15, contaminated these images by additive zero-mean Gaussian noise.

Case	Reference Pixels*	CDR (%)		FDR (%)		CR (%)		Noise†(σ2)	Angle (°)		ir vector			kh	K	Fisher Ratio
		I	Ii	I	Ii	I	Ii		θ	θi	[R	G	B]			FR	FRi
a	10,503	51	76	86	52	14	48	0.8 × 10−3	2	74	[−20	2	18]	0.97	5	3	4
b	18,340	67	84	44	30	56	70	2.0 × 10−3	35	78	[−24	13	11]	0.93	5	4	10
c	5,749	89	74	140	117	−40	−17	0.5 × 10−3	2	27	[−15	−4	19]	0.65	7	4	5
d	13,460	62	70	42	38	58	62	1.0 × 10−3	12	272	[−20	0	21]	0.95	6	4	28
e	10,097	57	85	47	23	53	77	1.5 × 10−3	40	262	[−31	0	31]	0.95	5	4	17
f	12,666	48	60	70	51	30	49	0.5 × 10−3	158	202	[−5	−8	13]	0.9	7	3	6
g	13,775	79	84	30	26	70	74	1.5 × 10−3	10	256	[−30	0	30]	0.93	5	8	16
h	12,231	70	80	64	62	36	38	0.8 × 10−3	1	94	[−26	14	12]	0.95	8	8	17
i	9,063	77	92	42	25	58	75	1.5 × 10−3	128	265	[−27	−5	31]	0.93	5	5	13
j	12,497	64	75	115	74	−15	26	1.0 × 10−3	14	344	[−13	2	10]	0.85	10	3	5
k	12,512	89	89	33	21	67	79	1.0 × 10−3	1	291	[−20	−8	27]	0.9	6	5	13
l	23,102	80	81	90	29	10	71	0.5 × 10−3	12	14	[−49	75	−26]	0.87	7	5	7
m	20,176	62	76	52	38	48	62	1.3 × 10−3	19	20	[−9	26	−17]	0.88	5	2	6
n	38,629	49	90	72	40	28	60	1.0 × 10−3	11	43	[−23	34	−11]	0.6	4	4	17
Average		67	80	66	45	34	55	1.0 × 10−3	32	160	[−22	10	12]	0.88	6	4	12

^*Segmented Object Reference Image, I original image, I_i injected image,

^†Additive Gaussian noise: N(0, σ²)

shows the results of the comparison of the same images, but contaminated by additive zero-mean Gaussian noise. As can be seen, results obtained with the colour injection technique for both tests are better than those obtained using only a Gaussian classification.

As a third phase of the tests, an example of image sequence segmentation is presented. In this case, each frame illumination has been modified before the segmentation process, in order to verify the advantage of our proposal against illumination changes. The illumination is applied to each frame in a uniform way. A zero-mean Gaussian noise with standard deviation n_p = 0.15I_O was also added to the pixels of the images. Moreover, a sinusoidal time variation in the luminous intensity has been set up.

With this example, we try to show the improvements in the segmentation phase when the colour injection preprocessing step proposed in this paper is used before the segmentation. In this example, the GMM technique is used as an on-line segmentation technique (the same used in the off-line process). The original image I is identified by I^k for each captured frame in time kT (k = 1, 2... and T = time between consecutive images), and its corresponding image after the colour injection, ${\mathrm{I}}_{\mathrm{i}}^k$, are segmented using the optimal class number obtained as a result of the off-line stage. In this case K_opt = 5.

For the images I^k and ${\mathrm{I}}_{\mathrm{i}}^k$, the GMM segmentation process is applied recursively using the a priori probabilities, means and variances obtained in the images I^k−1 and ${\mathrm{I}}_{\mathrm{i}}^{k-1}$, respectively. For the segmentation of the image ${\mathrm{I}}_{\mathrm{i}}^k$, the next steps are also added: (a) we obtain the pixels (seeds) in the RGB space of the object and background of the image ${\mathrm{I}}_{\mathrm{i}}^{k-1}$, (b) the vector i_r is subtracted from them, (c) they are transformed to the HSI space, (d) the truncation process described in Section 4 is applied, and, finally, (e) the sets ${\mathrm{O}}_{\mathit{RGB}}^k$ and ${\mathrm{B}}_{\mathit{RGB}}^k$ are obtained. These steps (a, b, c, d and e) represent the block: “Obtaining seeds: Object (O) and Background (B)”, for recursive segmentation in the block-diagram of the Figure 1.

In image sequence segmentation, as this example, the iterative process (seen in Section 6) has been slightly modified in order to reduce the processing time and to increase the stability of the colour injection in time. The first modification, is to use ${\theta }_{\text{opt}}^{k-1}$ (θ_opt of the previous frame) as a starting point to obtain ${\theta }_{\text{opt}}^k$, thus reducing the search interval to: $\left[{\theta }_{\text{opt}}^{k-1}-{\theta }_f,\mathrm{\hspace{0.17em} }{\theta }_{\text{opt}}^{k-1}+{\theta }_f\right]$. In the example of Figure 16, we have fixed experimentally θ_f = 12°, Δθ = 1° and k_h = 0.91. The second modification in the iterative process is that the optimal colour vector to inject ${\mathbf{i}}_{\mathbf{r}}^k$ is obtained recursively, using for the calculation of ${\theta }_{\text{opt}}^k$ the following expression: ${\theta }_{\text{opt}}^k=k_t{\theta }_{\text{opt}}^k+\left(1-k_t\right){\theta }_{\text{opt}}^{k-1}$, where k_t ∈ [1, 0] is the constant fixed to obtain a proper smoothing of the evolution of the different parameters involved in the colour injection. k_t has been fixed experimentally to 0.1.

The GMM technique is used in these tests, mainly to obtain a better adjustment of the K_opt Gaussians in each frame, and, therefore, to obtain the maximum quality in the object segmentation. Then, a reliable comparison of the segmentation quality between the segmentation of the images I and I_i in the time can be carried out, and the compensation effects in the segmentation against illumination changes, applying the colour injection or not, can be verified. However, as it is known, this technique may have a relatively high computational cost due to the convergence iterations of the EM algorithm, so, its use in video segmentation is sometimes limited. For the consecutive segmentation of an image sequence in real time, our proposal in this work is to track recursively the parameters that define each Gaussian: O and B, using the optimal estimation provided by the Kalman filter, tracking technique widely studied in the image processing field.

Figure 16 shows the results of the segmentation of the images I^k and ${\mathrm{I}}_{\mathrm{i}}^k$ of the example sequence, for the frames captured in k = 21, 42, 63, 84, 105, 126, 147, 168, 189 and 210. The respective mean intensities of these frames are: $I_m^{21}=0.530$, $I_m^{42}=0.613$, $I_m^{63}=0.672$, $I_m^{84}=0.698$, $I_m^{105}=0.658$, $I_m^{126}=0.572$, $I_m^{147}=0.510$, $I_m^{168}=0.403$, $I_m^{189}=0.307$ and $I_m^{210}=0.224$.

However, if the variation of the parameters of the different classes of the scene in the image sequence is very small, that is, when the scene is relatively uniform in the time with small illumination changes, the colour injection can be carried out applying the same colour vector i_r to each frame in the time kT, with no need to recalculate it. This is possible due to the illumination compensation effect previously mentioned in Section 7. In this sense, the segmentation can be carried out keeping the parameters of both Gaussians as fixed values in all the sequence. Then, the computational cost is noticeably reduced.

Figure 17 depicts the results of the segmentation of the images I^k and ${\mathrm{I}}_{\mathrm{i}}^k$ corresponding to the instants: k = 50, 100, 150, 200, 250 and 300 of the previous example image sequence, but, this time, without recalculating the colour vector i_r and with fixed parameters for both Gaussians. The objective of this example is to appreciate the improvement in the segmentation of the sequence of colour injected images, although the same colour vector i_r is used in the injection.

In Figure 17, the upper row depicts the I^k images, the central row shows the results of the segmentation without colour injection (I^k segmentation), and the lower one contains the results of the segmentations after the colour injection proposed in this work ( ${\mathrm{I}}_{\mathrm{i}}^k$ segmentation). The segmented images show the object pixels in green colour. The segmentation process used in this phase has been used in the first stage of the experimental tests.

As a reference, the average execution time (T_p) in Matlab of the on-line process for different M = N values is approximately: T_p = 74.9 ms. for N = 50, T_p = 80.0 ms. for N = 100, T_p = 85.4 ms. for N = 200, T_p = 95.9 ms. for N = 400, T_p = 117.3 ms. for N = 800 and T_p = 160.4 ms. for N = 1,600. The tests have been made with the following configuration: θ_f = 12° in the recursive process, 10% of pixels segmented in the previous frame are used to obtain the ${\mathrm{O}}_{\mathit{RGB}}^k$ and ${\mathrm{B}}_{\mathit{RGB}}^k$ sets, and the image size is 346 × 421 pixels. The image size affects the execution time of the injection of i_r to the original image, and the conversion of the injected image to the HS plane for its posterior segmentation. The tests have been carried out in a PC with a processor Intel Core 2 Duo with a 2.4 GHz frequency.

Finally, we show some results of the real-time segmentation of images captured in a scene with significative illumination changes. These results highlight again the advantages of using the colour injection proposal presented in this paper. Figure 18 depicts the comparative results in two columns: the left column (a) shows the segmented images without the colour injection, and in the right one (b) the images segmented after applying the colour injection.

The segmentation has been performed by thresholding the pdf of the skin class seen in (28), once all the classes have been obtained with the GMM algorithm. In this case, K = 10 predefined classes were used. In order to demonstrate the robustness to illumination changes, an incandescent light bulb has been used (that produces a hue change in the whole image that tends to yellow) to really change the illumination of the scenes. The different luminous Intensity levels have been quantified with the mean intensity of the image normalized between [0, 1]. The corresponding Intensity levels for the five images of each column of Figure 18, starting from the image above, are: I₁ = 0.351, I₂ = 0.390, I₃ = 0.521, I₄ = 0.565, I₅ = 0.610.

In the performance of this last practical test, a PC with an Intel Quad Core Q6600 @ 2.4 GHz processor and 2 GB SDRAM @ 633 MHz memory has been used. Although it is a last generation PC with four processing cores (CPUs), our application has only used a single CPU. A Fire-Wire video camera with a 1/2” CCD sensor with a 640 × 480 spatial resolution and an image capture rate of 30 fps (RGB without compression) was used. The optic used is a C-Mount of 3/4” with a focal length of f = 12 mm. The different algorithms of our proposal (GMM, colour injection and segmentation) have been developed in C, under Linux OpenSuSE10.3 (×86_64) operating system. With this configuration, the average processing time of the on-line process (T_p) is approximately 2 ms for N = 50.

9. Conclusions

A method to increase the separation between two classes in a pixel classification process has been proposed. The experimental results demonstrate that injecting colour in the captured image guarantees good results in maximizing the class separation, implying that class distributions adopt more Gaussian shapes, and, therefore, the segmentation of the desired object improves.

Its practical implementation results are simple and the process time is small. Even though the algorithm needs to calculate both class deviations in each iteration, these are easy to obtain, considering that classes are formed by a limited number of samples (N), the increase of θ_i is not very small, Δθ = 1°, and the search interval is not very wide: θ_f = 12°. This implies that calculations are relatively fast.

In this work, the expressions of interest to understand the vector’s behaviour in the HSI space have been demonstrated from the respective statistics in the RGB space. Moreover, the equations to convert directly from YC₁C₂ colour space to HSI space have been obtained.

Finally, we should indicate that the images have been directly obtained from the classification process without any other auxiliary stage, such as morphological operations.

For future work, our research is currently focused on the injection of a vector i_r with a non-zero mean, as a function of the intensity mean desired in the image, to increase the compensation of the effects caused by the illumination changes. We are also developing the hue and saturation dispersion model when the classes are translated all over the HS plane, using the C₁C₂ plane, (similar to the hue and saturation deviation estimation that is made in [31] for the HSI space defined in [24]). This will diminish the processing time, because it will not be necessary to calculate the hue and saturation variances of both classes in each iteration. Finally, we are doing research into the class separation applying higher order transformations that imply scales and rotations of the classes in the C₁C₂ plane. This could solve part of the intrinsic limitations of the colour injections for just adding the vector i_r.