1. Introduction
Indoor navigation has become an essential technique that can be applied in a number of settings, such as in a supermarket as a shopping guide, for a fire emergency service for navigation, or for a hospital patient for tracking. However, some techniques that have been successfully used that are similar to the Global Navigation Satellite System (GNSS) [
1,
2,
3] are not suitable for indoor navigation. Real-time indoor positioning using existing techniques remains a challenge, and this is a bottleneck in the development of indoor location-based services (LBSs) [
4].
The solution for indoor positioning is increasingly regarded as being based on the integration of multiple technologies, e.g., WiFi, ZigBee, inertial navigation systems (INSs), and laser scanning systems (LSSs). Each has its shortcomings, but an integrated system can combine the advantages of several of these technologies. Pahlavan and Li reviewed the technical aspects of the existing technologies for wireless indoor location systems [
5]. There are two main hardware layouts that can be used in an indoor situation: (1) a sensor network, such as a WiFi or ZigBee system [
6,
7,
8]; and (2) self-contained sensors, such as gyroscopes, accelerometers or magnetometers [
9,
10,
11,
12]. However, the stringent demands of reliable and continuous navigation in indoor environments are unlikely to be achievable using a single type of layout, and developing a hybrid scheme for reliable and continuous positioning is therefore a core prerequisite for real-time indoor navigation [
13,
14,
15].
It is well recognized that trilateration and fingerprint matching are two basic WiFi-based approaches to locating an object in an indoor environment. In the first method, the user coordinates are calculated based on the distances between access points (APs) and the user. However, the distance measured based on the WiFi signal path loss model is so unstable that it is impossible to use such measurements in a practical indoor navigation system. Fingerprint matching is a more practical approach for use in a market-orientated indoor navigation system, and this technique has been widely researched, especially with the rapid market penetration of the modern smartphone. APs in supermarkets, schools, hospitals, and other infrastructures are also freely available for fingerprint database establishment. Artificial intelligence (AI) methods, e.g., decision trees and neural networks, constitute a new possible approach to determining a user’s location [
16]. Nevertheless, some inevitable shortcomings exist, e.g., tedious fingerprint database updates and the need to alleviate the “go and back” phenomenon by integrating other techniques [
5,
16,
17]. In addition, the cost of continuously using the WiFi radio on a mobile device can be prohibitive. Nonetheless, such methods are the focus of significant research efforts [
12].
Pedestrian dead reckoning (PDR) algorithms, based on accelerometer, gyroscope and magnetometer measurements, can be used as a complementary method of developing an indoor navigation system. The basic PDR procedure involves step detection, step length estimation and heading determination [
4,
17]. In practice, acceleration measurements are an ideal choice for step detection, considering the periodicity of a pedestrian’s walking pattern, and there are three types of step detection algorithms: peak detection, flat-zone detection and zero-crossing detection. The deficiencies of the peak and zero-crossing detection algorithms create the potential for missing detection or over-detection if the thresholds are not appropriately set, and over-detection may also occur in the case of the flat-zone detection algorithm because the flat-zone test statistic varies with different walking patterns [
18]. Considerable research has been conducted in an attempt to improve the accuracy of step length estimation, and the techniques that have been developed for this purpose can be summarized as constant/quasi-constant models, linear models, nonlinear models, and AI models [
19]. A look-up table conveniently stores a few levels of step length for a given pedestrian based on his/her locomotion mode and the time duration of every step [
20]. The linear relationship between step length and step frequency can be used to estimate step length. Kourogi and Kurata utilized the correlation between vertical acceleration and walking velocity to compute the walking speed and then estimated the step length by multiplying the walking speed by the time of the unit cycle of locomotion [
17]. Cho presented a neural network for step length estimation that is unaffected by accelerometer bias and the acceleration of gravity [
21]. A gyroscope and a magnetometer are two types of heading sensors that are typically used when the PDR algorithm is applied [
22]. Klingbeil and Xiao proposed the concept of correcting the magnetic azimuth using gyro data collected over a short time, thereby allowing the heading angles to be estimated by combining gyroscope and magnetometer measurements [
22,
23]. A biaxial magnetic compass may be used to calculate the azimuth after compensating for the inclination of the compass using a shoe-mounted accelerometer [
21]. The use of an INS/EKF framework to reduce heading drift has been demonstrated [
11]. A detector has been proposed that can perform magnetic field measurements, which can be used for heading estimation with adequate accuracy. This detector utilizes different magnetic field test parameters that can be analyzed to produce good magnetic field measurements [
24]. One factor that limits the use of PDR alone for indoor navigation is its susceptibility to cumulative errors over time. To improve the reliability and accuracy of a PDR navigation system, the gross error caused by the sensor’s raw observations must also be avoided. To this end, an electromyography (EMG) method was presented and compared with a traditional method based on accelerometers in several field tests, and the results demonstrated that the EMG-based method was effective and that its performance in combination with a PDR algorithm can be comparable to that of accelerometer-based methods [
24,
25].
To overcome these constraints, a floor map can be used to further calibrate the bias and correct for unreasonable positioning results. For example, combining gyroscope measurements with the use of a floor map allows the orientation to be corrected using only map aids [
26,
27], and large heading errors are eliminated via the long-range geometrical constraints exploited by particle filters (PFs) [
28]. Extending these techniques to multiple floors and stairways could also be made possible by significantly adapting their constraints to suit pedestrians [
29,
30]. Unfortunately, the large number of particles makes it unrealistic to operate such algorithms in a real-time manner. However, the integration of several techniques can dramatically reduce the number of particles required in a PF model.
To summarize, the methodologies of the whole article is concluded below:
- (1)
Theoretical analysis. A series of basic researches have been analyzed. As mentioned in the introduction, the signal-based network such as Fingerprint System, and INSs should be two fundamental techniques in indoor localization. However, the stringent demands of reliable and continuous navigation in indoor environments are unlikely to be achievable using a single type of layout, and developing a hybrid scheme for reliable and continuous positioning is therefore a core prerequisite for real-time indoor navigation. The aim is to overcome the drawbacks of conventional architectures at theoretical level to make it possible to improve the performance of an integrated WiFi/pseudo-odometry system.
- (2)
Integration Methodology Development. In the past, extended or unscented Kalman filter (EKF, UKF) and Particle Filter (PF) have mainly been used in data processing. However, in various cases as indicated in the introduction section, the situation is a little different. For instance, the noise dealt with by Kalman filter is assumed to be white noise, and PF algorithm requires a large amount of calculation. To overcome these constraints, a floor map can be used to further calibrate the bias and correct for unreasonable positioning results.
- (3)
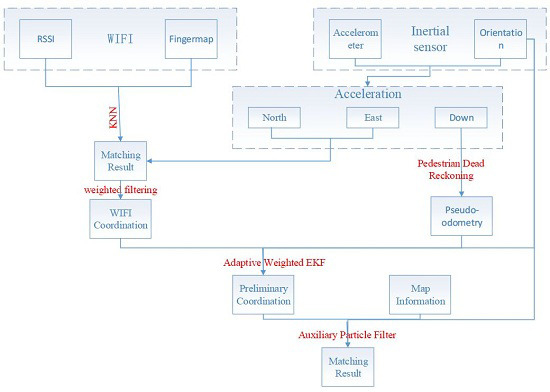
Physical System Implementation and Tests. The specific course is shown in
Figure 1 below:
Figure 1.
The general flow-chart.
Figure 1.
The general flow-chart.
In this paper, a scheme for indoor positioning by fusing floor map, WiFi and smartphone sensor data to obtain a real-time hybrid indoor navigation result is presented. Compared with the existing technology, Topology-Constrained KNN Positioning method introduced the floor map as a constraint, which could improve the accuracy and operational speed of the WiFi result. Besides, this method fits linear zones much better, such as corridors and narrow roads, which would be hard for GPS to fit, and the most useful places for WiFi localization technology. On the other hand, the multi-threshold PDR algorithm, presented in this paper, could clearly detect most steps accurately in the experiment. In addition, pseudo-odometry (P-O) is presented in this paper as a new exclusive term which means that by simulating the odometer, the step lengths are transformed to the time-domain (TD). The remainder of the paper is organized as follows: In
Section 2, a topology-constrained KNN positioning algorithm is proposed, and
Section 3 proposes a pseudo-odometry measurement simulation procedure based on a multi-threshold PDR algorithm. Subsequently, a WIFI/P-O integration scheme based on a fading-factor-based EKF is demonstrated in
Section 4. Thereafter,
Section 5 presents a scheme for floor-map-aided integration based on a PF, which is the core of the hybrid integration scheme. Finally, two experiments are analyzed in
Section 6, and
Section 7 concludes the paper.