The Effect of Personalization on Smartphone-Based Fall Detectors
Abstract
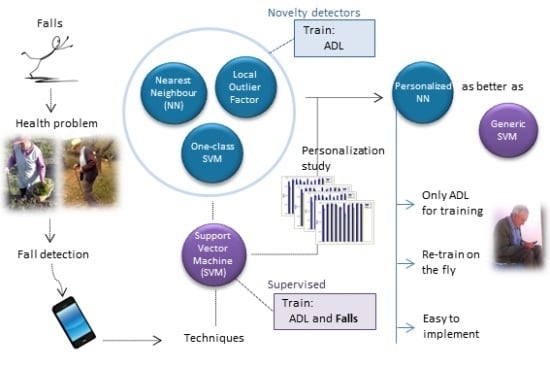
:1. Introduction
- The characteristics of sensors integrated in smartphones are not as good as their counterparts in dedicated devices. Existing fall datasets are recorded using smartphones with accelerometers of a range of only ±2 g (g = gravity acceleration). Modern devices include accelerometers with higher ranges (3–16 g), so this problem may be mitigated in the future.
- Battery life is still a limitation and unnecessary computation in the phone should be avoided.
- The lack of real-world fall data is common to many fall detector studies. Most studies are based on laboratory falls performed by young or mature healthy people. Few studies include real-life data, but the number of falls is still low and there is no public dataset.
- Instead of building a generic fall detector, it would be interesting to adapt the detector to each user, since the movements and requirements depend on the context: a fall in the construction industry, a fall from a bed in a hospital, a fall of an older person, a fall of a person suffering from movement disorders, etc.
2. Experimental Section
2.1. Dataset
2.2. Algorithms and Their Evaluation

- First, we have compared the novelty detectors between them and selected the best one using a conventional cross-validation strategy (Section 3.1).
- Then, the selected novelty detector (NN) has been compared with SVM subject by subject, thus trying to study personalization, which is the main focus of this paper (Section 3.2).

3. Results
3.1. Comparison between Novelty Detectors
| NN | LOF | OneClass-SVM |
| 0.9809 ± 0.0028 | 0.9784 ± 0.0048 | 0.9644 ± 0.0051 |
| Differences | ||
| NN-LOF | NN-OneClass-SVM | LOF-OneClass-SVM |
| 0.0025 ± 0.0066 | 0.0165 ± 0.0039 | 0.0140 ± 0.0083 |
| p-value | ||
| 0.27 | <0.01 | <0.01 |
| NN | LOF | OneClass-SVM | |
|---|---|---|---|
| SE | 0.9541 ± 0.0064 | 0.9622 ± 0.0189 | 0.9156 ± 0.0123 |
| SP | 0.9484 ± 0.0059 | 0.9364 ± 0.0199 | 0.9417 ± 0.0083 |
| 0.9512 ± 0.0046 | 0.9491 ± 0.0142 | 0.9285 ± 0.0091 |
3.2. Personalization
| User | Algorithm | |||
|---|---|---|---|---|
| PNN | GNN | PSVM | GSVM | |
| 1 | 0.9770 ± 0.0058 | 0.9463 ± 0.0097 | 0.9881 ± 0.0039 | 0.9667 ± 0.0063 |
| 2 | 0.9877 ± 0.0101 | 0.9829 ± 0.0092 | 0.9929 ± 0.0069 | 0.9905 ± 0.0079 |
| 3 | 0.9900 ± 0.0060 | 0.9713 ± 0.0059 | 0.9948 ± 0.0043 | 0.9912 ± 0.0067 |
| 4 | 0.9878 ± 0.0067 | 0.9744 ± 0.0064 | 0.9930 ± 0.0053 | 0.9845 ± 0.0046 |
| 5 | 0.9760 ± 0.0074 | 0.9720 ± 0.0069 | 0.9766 ± 0.0068 | 0.9745 ± 0.0095 |
| 6 | 0.9903 ± 0.0072 | 0.8460 ± 0.0341 | 0.9967 ± 0.0030 | 0.9405 ± 0.0127 |
| 7 | 0.9780 ± 0.0108 | 0.9554 ± 0.0140 | 0.9870 ± 0.0065 | 0.9905 ± 0.0028 |
| 8 | 0.9863 ± 0.0032 | 0.9591 ± 0.0048 | 0.9957 ± 0.0054 | 0.9724 ± 0.0037 |
| 9 | 0.9909 ± 0.0099 | 0.9894 ± 0.0087 | 0.9949 ± 0.0072 | 0.9952 ± 0.0054 |
| 10 | 0.9967 ± 0.0009 | 0.9855 ± 0.0036 | 0.9942 ± 0.0014 | 0.9892 ± 0.0023 |
| Mean | 0.9861 ± 0.0023 | 0.9582 ± 0.0042 | 0.9914 ± 0.0017 | 0.9795 ± 0.0022 |




| User | PNN | GNN | PSVM | GSVM | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SE | SP | SE | SP | SE | SP | SE | SP | |||||
| 1 | 0.9216 | 0.9817 | 0.9511 | 0.8980 | 0.9656 | 0.9311 | 0.9510 | 0.9655 | 0.9580 | 0.9333 | 0.9742 | 0.9535 |
| 2 | 0.9906 | 0.9682 | 0.9792 | 0.9774 | 0.9429 | 0.9599 | 1.0000 | 0.9627 | 0.9811 | 0.9962 | 0.9594 | 0.9776 |
| 3 | 0.9737 | 0.9740 | 0.9738 | 0.9105 | 0.9625 | 0.9360 | 0.9816 | 0.9750 | 0.9781 | 0.9763 | 0.9625 | 0.9693 |
| 4 | 0.9648 | 0.9689 | 0.9667 | 0.9500 | 0.9661 | 0.9579 | 0.9907 | 0.9605 | 0.9754 | 0.9648 | 0.9717 | 0.9681 |
| 5 | 0.9154 | 0.9316 | 0.9230 | 0.9019 | 0.9377 | 0.9186 | 0.9346 | 0.9304 | 0.9322 | 0.9212 | 0.9450 | 0.9325 |
| 6 | 0.9880 | 0.9728 | 0.9803 | 0.9560 | 0.7990 | 0.8735 | 1.0000 | 0.9852 | 0.9926 | 0.9960 | 0.8365 | 0.9126 |
| 7 | 0.9815 | 0.9577 | 0.9694 | 0.9704 | 0.9240 | 0.9467 | 0.9815 | 0.9859 | 0.9837 | 0.9759 | 0.9690 | 0.9724 |
| 8 | 0.9623 | 0.9878 | 0.9749 | 0.9113 | 0.9443 | 0.9274 | 0.9811 | 0.9895 | 0.9853 | 0.9509 | 0.9827 | 0.9667 |
| 9 | 0.9882 | 0.9772 | 0.9826 | 0.9824 | 0.9590 | 0.9703 | 0.9980 | 0.9863 | 0.9921 | 0.9863 | 0.9795 | 0.9828 |
| 10 | 0.9787 | 0.9950 | 0.9868 | 0.9574 | 0.9825 | 0.9699 | 0.9787 | 0.9925 | 0.9856 | 0.9468 | 0.9925 | 0.9693 |
| Mean | 0.9665 | 0.9715 | 0.9688 | 0.9415 | 0.9384 | 0.9391 | 0.9797 | 0.9734 | 0.9764 | 0.9648 | 0.9573 | 0.9605 |
| PNN vs. GNN | PSVM vs. GSVM | PNN vs. GSVM | PNN vs. PSVM | |||||
|---|---|---|---|---|---|---|---|---|
| SE | 10 | 0 | 10 | 0 | 4 | 6 | 0 | 10 |
| SP | 9 | 1 | 6 | 4 | 6 | 4 | 5 | 5 |
| 10 | 0 | 9 | 1 | 5 | 5 | 1 | 9 | |
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- World Health Organization (WHO). Global Report on Falls Prevention in Older Age. Available online: http://www.who.int/ageing/publications/en/ (accessed on 15 January 2016).
- The 2012 Ageing Report. European Commission 2012. Available online: http://ec.europa.eu/economy_finance/publications/european_economy/2012/pdf/ee-2012–2_en.pdf (accessed on 3 November 2015).
- Rubenstein, L.Z.; Josephson, K.R. The epidemiology of falls and syncope. Clin. Geriatr. Med. 2002, 18, 141–158. [Google Scholar] [CrossRef]
- Williams, V.; Victor, C.; McCrindle, R. It Is Always on Your Mind: Experiences and Perceptions of Falling of Older People and Their Carers and the Potential of a Mobile Falls Detection Device. Available online: http://www.hindawi.com/journals/cggr/2013/295073/ (accessed on 15 January 2016).
- Hawley-Hague, H.; Boulton, E.; Hall, A.; Pfeiffer, K.; Todd, C. Older adults’ perceptions of technologies aimed at falls prevention, detection or monitoring: A systematic review. Int. J. Med. Inform. 2014, 83, 416–426. [Google Scholar] [CrossRef] [PubMed]
- Saverino, A.; Moriarty, A.; Playford, D. The risk of falling in young adults with neurological conditions: A systematic review. Disabil. Rehabil. 2014, 36, 963–977. [Google Scholar] [CrossRef] [PubMed]
- Noury, N.; Fleury, A.; Rumeau, P.; Bourke, A.K.; Laighin, G.O.; Rialle, V.; Lundy, J.E. Fall detection-principles and methods. In Proceedings of the International Conference of IEEE EMBS, Paris, France, 22–26 August 2007.
- Yu, X. Approaches and principles of fall detection for elderly and patient. In Proceedings of the 10th International Conference on E-Health Networking, Applications and Services, Health-Com, Singapore, 7–9 July 2008; pp. 42–47.
- Igual, R.; Medrano, C.; Plaza, I. Challenges, Issues and Trends in Fall Detection Systems. Available online: http://download.springer.com/static/pdf/780/art%253A10.1186%252F1475-925X-12-66.pdf?originUrl=http%3A%2F%2Fbiomedical-engineering-online.biomedcentral.com%2Farticle%2F10.1186%2F1475-925X-12-66&token2=exp=1452831171~acl=%2Fstatic%2Fpdf%2F780%2Fart%25253A10.1186%25252F1475-925X-12-66.pdf*~hmac=a2b7c6ac9951dc86e9c8af78a2a6ea00bfbdd5e99874b8d92b36661487e7a8e5 (access on 15 January 2016).
- Schwickert, L.; Becker, C.; Lindemann, U.; Marechal, C.; Bourke, A.; Chiari, L.; Helbostad, J.L.; Zijlstra, W.; Aminian, K.; Todd, C.; et al. Fall detection with body-worn sensors: A systematic review. Z. Gerontol. Geriatr. 2013, 46, 706–719. [Google Scholar] [CrossRef] [PubMed]
- Habib, M.A.; Mohktar, M.S.; Kamaruzzaman, S.B.; Lim, K.S.; Pin, T.M.; Ibrahim, F. Smartphone-based solutions for fall detection and prevention: Challenges and open issues. Sensors 2014, 14, 7181–7208. [Google Scholar] [CrossRef] [PubMed]
- Sposaro, F.; Tyson, G. iFall: An Android application for fall monitoring and response. In Proceedings of the International Conference of IEEE EMBS, Minneapolis, MI, USA, 2–6 September 2009.
- Dai, J.; Bai, X.; Yang, Z.; Shen, Z.; Xuan, D. Mobile phone-based pervasive fall detection. Pers. Ubiquitous Comput. 2010, 14, 633–643. [Google Scholar] [CrossRef]
- Bagala, F.; Becker, C.; Cappello, A.; Chiari, L.; Aminian, K.; Hausdorff, J.M.; Zijlstra, W.; Klenk, J. Evaluation of Accelerometer-Based Fall Detection Algorithms on Real-World Falls. PLoS ONE 2012, 7, e37062. [Google Scholar] [CrossRef] [PubMed]
- Abbate, S.; Avvenuti, M.; Bonatesta, F.; Cola, G.; Corsini, P.; Vecchio, A. A smartphone-based fall detection system. Pervasive Mob. Comput. 2012, 8, 883–899. [Google Scholar] [CrossRef]
- Albert, M.V.; Kording, K.; Herrmann, M.; Jayaraman, A. Fall classification by machine learning using mobile phones. PLoS ONE 2012, 7, e36556. [Google Scholar] [CrossRef] [PubMed]
- Boulos, M.N.K.; Wheeler, S.; Tavares, C.; Jones, R. How smartphones are changing the face of mobile and participatory healthcare: an overview, with example from eCAALYX. BioMed. Eng. Online 2011, 10, 24. [Google Scholar] [CrossRef] [PubMed]
- Igual, R.; Plaza, I.; Martín, L.; Corbalan, M.; Medrano, C. Guidelines to Design Smartphone Applications for People with Intellectual Disability: A Practical Experience. Ambient Intelligence—Software and Applications. In Advances in Intelligent Systems and Computing; van Berlo, A., Hallenborg, K., Rodríguez, J.M.C., Tapia, D.I., Novais, P., Eds.; Springer International Publishing: Cham, Switzerland, 2013. [Google Scholar]
- Medrano, C.; Igual, R.; Plaza, I.; Castro, M. Detecting Falls as Novelties in Acceleration Patterns Acquired with Smartphones. PLoS ONE 2014, 9, e94811. [Google Scholar] [CrossRef] [PubMed]
- Brownsell, S.; Hawley, M.S. Automatic fall detectors and the fear of falling. J. Telemed. Telecare 2004, 10, 262–266. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Lockhart, T.E. Automatic individual calibration in fall detection—An integrative ambulatory measurement framework. Comput. Methods Biomech. Biomed. Eng. 2013, 16, 504–510. [Google Scholar] [CrossRef] [PubMed]
- Sekine, M.; Tamura, T.; Togawa, T.; Fukui, Y. Classification of waist-acceleration signals in a continuous walking record. Med. Eng. Phys. 2000, 22, 285–291. [Google Scholar]
- Weiss, G.M.; Lockhart, J.W. The Impact of Personalization on Smartphone-Based Activity Recognition. Available online: https://www.researchgate.net/profile/Gary_Weiss/publication/268188348_The_Impact_of_Personalization_on_Smartphone-Based_Activity_Recognition/links/54fefa910cf2741b69f1e044.pdf (accessed on 15 January 2016).
- Markou, M.; Singh, S. Novelty detection: A review-part 1: Statistical approaches. Signal Process. 2003, 83, 2481–2497. [Google Scholar] [CrossRef]
- Markou, M.; Singh, S. Novelty detection: A review-part 2: Neural network based approaches. Signal Process. 2003, 83, 2499–2521. [Google Scholar] [CrossRef]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection: A survey. ACM Comput. Surv. 2009, 41. [Google Scholar] [CrossRef]
- Medrano, C.; Igual, R.; Plaza, I.; Castro, M.; Fardoun, H.M. Personalizable Smartphone Application for Detecting Falls. In Proceedings of the International Conference on Biomedical and Health Informatics, Valencia, Spain, 1–4 June 2014.
- Igual, R.; Medrano, C.; Plaza, I. A comparison of public datasets for acceleration-based fall detection. Med. Eng. Phys. 2015, 37, 870–878. [Google Scholar] [CrossRef] [PubMed]
- Noury, N.; Rumeau, P.; Bourke, A.K.; OLaighin, G.; Lundy, J.E. A proposal for the classification and evaluation of fall detectors. IRBM 2008, 29, 340–349. [Google Scholar] [CrossRef]
- Breunig, M.M.; Kriegel, H.P.; Ng, R.T.; Sander, J. LOF: Identifying density-based local outliers. In Proceedings of the ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 15–18 May 2000; pp. 93–104.
- Schölkopf, B.; Platt, J.C.; Shawe-Taylor, J.C.; Smola, A.J.; Williamson, R.C. Estimating the support of a high-dimensional distribution. Neural Comput. 2001, 13, 1443–1471. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.C.; Linc, C.J. LIBSVM: A library for Support Vector Machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 27:1–27:27. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013; Available online: http://www.R-project.org/ (accessed on 15 January 2015).
- Amer, M.; Goldstein, M.; Abdennadher, S. Enhancing one-class support vector machines for unsupervised anomaly detection. In Proceedings of the ACM SIGKDD Workshop on Outlier Detection and Description, Chicago, IL, USA, 11 August 2013; pp. 8–15.
- Klenk, J.; Becker, C.; Lieken, F.; Nicolai, S.; Maetzler, W.; Alt, W.; Zijlstra, W.; Hausdorff, J.M.; van Lummel, R.C.; Chiari, L.; et al. Comparison of acceleration signals from simulated and real-world backward falls. Med. Eng. Phys. 2011, 33, 368–373. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Medrano, C.; Plaza, I.; Igual, R.; Sánchez, Á.; Castro, M. The Effect of Personalization on Smartphone-Based Fall Detectors. Sensors 2016, 16, 117. https://doi.org/10.3390/s16010117
Medrano C, Plaza I, Igual R, Sánchez Á, Castro M. The Effect of Personalization on Smartphone-Based Fall Detectors. Sensors. 2016; 16(1):117. https://doi.org/10.3390/s16010117
Chicago/Turabian StyleMedrano, Carlos, Inmaculada Plaza, Raúl Igual, Ángel Sánchez, and Manuel Castro. 2016. "The Effect of Personalization on Smartphone-Based Fall Detectors" Sensors 16, no. 1: 117. https://doi.org/10.3390/s16010117
APA StyleMedrano, C., Plaza, I., Igual, R., Sánchez, Á., & Castro, M. (2016). The Effect of Personalization on Smartphone-Based Fall Detectors. Sensors, 16(1), 117. https://doi.org/10.3390/s16010117