1. Introduction
With the exponential growth of mobile data driven by various communication applications, such as WIFI and smartphones, the traditional wireless network via macrocell base stations (BSs) can not satisfy higher communication requirements (e.g., throughput and coverage). As a new candidate technology in the fifth generation (5G) wireless communication networks, heterogeneous network is proposed to improve network coverage and data rate [
1,
2,
3]. In heterogeneous networks, many femtocells with low-cost and low-energy consumption are distributed around macro BSs randomly meanwhile femtocell users (FUs) share the same spectrum resource with macrocell users (MUs) to obtain better spectral efficiency (e.g., co-channel development) and supplement traditional single-tier cellular systems. However, the cross-tier interference from femtocell users to macrocell receivers should be controlled severely. Therefore, interference mitigation is very important for which power control-based resource allocation (i.e., power allocation) has been a feasible method for Heterogeneous wireless networks (HetNets) [
4,
5].
The design of resource allocation algorithms in HetNets has attracted much research interest owing to its importance. The main task in resource allocation of underlay femtocell networks is to reduce the interference power received at MUs and simultaneously obtain the expected performance of femtocells, such as maximize the throughput of femtocells. To achieve this objective, various resource allocation (i.e., power control) algorithms have been extensively studied for various scenarios in [
6,
7,
8]. In [
6], a resource allocation problem in both the uplink and the downlink for two-tier femtocell networks is considered for maximizing the capacity of sensitive FUs and delay-tolerant FUs under the cross-tier interference constraint of MU and the quality-of-service (QoS) constraint of delay-sensitive users. In [
7], the authors propose an interference mitigation strategy to improve the uplink throughput by setting a fixed interference threshold and adjusting the maximum transmit power of femtocell user. To enhance the energy efficiency (EE) of HetNet, in [
8], two EE resource allocation algorithms via game theory are proposed for downlink transmission in multichannel macro-femto networks. Note that all the literatures above are designed based on the assumption of perfect knowledge of channel state information (CSI) at the transmitters. Although they have generally been assumed that complete system information (i.e., perfect channel state information) are available to FUs, nevertheless, due to the random nature of wireless channels and inaccurate channel estimation, as well as channel delays, it is impossible for FUs to obtain exact values of system parameters, such as channel gains and interference power from other networks.
In fact, due to lack of cooperation between macrocell networks and femtocell networks, obtaining complete system information pertaining to MUs is difficult for FUs. For instance, uncertain channel gains between FUs and MUs’ receivers may cause the sum aggregated interference of FUs on the MUs’ receivers to exceed the tolerable threshold, which means that the QoS requirements of users in the macrocell can not be guaranteed. As a result, from the perspective of MUs, this would increase the outage probability of MUs. Additionally, uncertainties on channel gains between femtocell BS and FUs’ receivers may also reduce the minimum rate requirement or actual signal-to-interference-plus-noise-ratio (SINR) of each FU at its femtocell BS or receiver below the target threshold. Therefore, the robustness of resource allocation algorithms should be considered ahead of time.
Thanks to robust optimization theory [
9,
10], robust resource allocation algorithms under imperfect CSI have drawn considerable attentions to overcome the effect of uncertainties in HetNets. Generally, the robust resource allocation designs are developed by two types of CSI errors, i.e., worst-case model and stochastic model [
11]. The deterministic model assumes that the instantaneous value of uncertain parameter is bounded by the worst-case upper boundary (e.g., ellipsoidal uncertainty sets), which aims to obtain the worst-case robustness and guarantee. On the contrary, the stochastic approach assumes that the statistical information of CSI or channel estimation errors is known at the transmitters and seeks to a suboptimal solution for maintaining a certain outage probability on average, such as probabilistic SINR constraint. In [
12], with the consideration of ellipsoidal uncertainty sets, Vaezpour et al. propose a robust distributed resource allocation algorithm in orthogonal frequency division multiple access (OFDMA) based femtocell networks that maximizes the total rate of FUs under the constraints on the minimum data requirement of each FU and the co-tier as well as cross-tier interference. In [
13], based on a robust Stackelberg game, a downlink power control scheme under column-wise uncertainty model is proposed for maximizing the capacities of each FU and each MU, where the impact of uncertainty and Nash equilibrium point are analyzed by using variational inequality (VI) and Stackelberg game theory respectively. In [
14], taking the ellipsoidal channel uncertainties into account, Xiao et al. present a robust resource allocation algorithm in full-duplex based OFDMA femtocell HetNets considering the throughput maximization of the femtocell while avoiding harmful interference to the macrocell. In [
15], based on game theory, a robust power control scheme for heterogeneous users is proposed by taking the bounded channel uncertainties into account. In [
16], Xu et al. propose a robust resource allocation algorithm for multiuser HetNets with macrocells and microcells through geometrical programming method. However, in practice, the case of worst-case estimation error may not always exist so that the proposed algorithms sacrifice system performance in a large part.
Moreover, the upper bound of uncertainty can not be easily obtained in practical Heterogeneous systems. Nevertheless, the robust resource allocation problem with Bayesian approach (i.e., probability constraint [
17]) is more appropriate for stochastic scenario because of the stochastic nature of measurements and estimation errors in wireless networks. In [
18,
19], based on the hierarchical game theory, Liu et al. propose a robust uplink power allocation algorithm to minimize the transmit power of FUs for two-tier femtocell networks sharing the same frequency with macrocells, where the uncertainties of channel gains are formulated as the probabilistic constraints. But these algorithms aim to minimize the power consumption, and thus cannot be used for the rate maximization in HetNets under channel uncertainties. In [
20], Mokari et al. investigate the robust quantized ergodic resource allocation scheme to achieve the sum-rate maximization of femtocell network while guaranteeing the macro network interference requirements with any desired high probability. However, only channel gains of interference links subject to probability constraint are considered. They do not consider the uncertainty of signal links. In [
21], for a two-tier HetNet, a robust MISO transmit power optimization problem is considered to design a minimum power downlink beamformer under the outage-based QoS constraints. However, all the aforementioned work only focuses on the protections of MUs in outage-based form (e.g., probabilistic cross-tier interference constraint of each MU). Under channel uncertainties, both the rate requirement of each FU and the performance protection of MUs should be considered simultaneously. Furthermore, the sensitivity analysis should be given to address the robustness of the scheme. The summary of the related work about resource allocation of HetNets is listed in
Table 1.
In this paper, we consider the robust uplink resource allocation algorithm in a two-tier heterogeneous network under the stochastic model. We assume that there is a maco BS serving multiple MUs, and multiple femto BSs intending to serve their own FUs inside the macrocell network’s coverage. In our formulation, we maximize the sum data rate of all FUs under the outage probability constraints that the cross-tier interference of MU and the rate requirement of FU are considered. Our main contributions are summarized as follows:
A multiuser resource allocation model for a two-tier HetNet is built. In this paper, we consider that the perfect CSI in both interference links (i.e., from the FUs to MUs) and signal links (i.e., the signal links of femtocell network) are not obtained while the channel uncertainties of the cross-tier interference constraints of MUs and the minimum rate constraint of each FU are formulated into the probability constraints. The existing works only consider the uncertainties in interference links from FUs to MUs, which ignores the effect of channel uncertainties from inter-tier links among FUs. Due to channel uncertainties, the original problem is non-convex and computationally intractable.
Furthermore, the original non-convex optimization problem is transformed into two different problems under no CSI feedback and partial CSI. Unlike traditional Bernstein inequality approximation approach with high computational complexity, however, in this paper, both of outage-based interference and rate constraints are transformed into the closed-form approximations by some algebraic transformation. A sub-optimal algorithm is proposed to solve the robust mixed integer programming problem by using the Lagrange dual decomposition and the sub-gradient method.
Thirdly, the computational complexity and sensitivity analysis (i.e., the impacts of uncertain parameters) of the proposed algorithm are given in this paper. Simulation results demonstrate the effectiveness of the proposed algorithm in terms of converge performance by comparing with the existing robust power control algorithm.
The rest of this paper is organized as follows.
Section 2 introduces the system model.
Section 3 gives the robust resource allocation problem.
Section 4 gives the transformation of outage probability constraint and shows the robust power allocation algorithm. And, the performance analysis and Simulation results are provided in
Section 5, and conclusions are drawn in
Section 6.
2. System Model
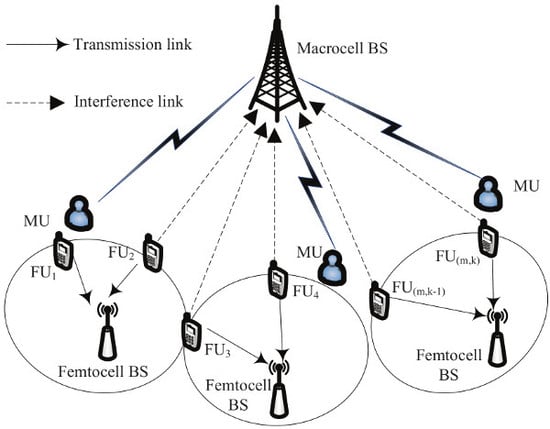
We consider a multiuser OFDM uplink HetNet comprising
M FUs communicating with their femtocell BSs over
K subcarriers. The FUs can utilize the spectrum resource of MUs by femtocell BSs opportunistically, as shown in
Figure 1. Note that both
M and
K vary based on the number of active users and available vacant subcarriers dynamically, and indexed by
and
respectively. Suppose that both of BSs and user equipments (UEs) have single antenna. Further, we assume
, and the bandwidth of each subcarrier is assumed to be
B Hz which is much less than the coherent bandwidth of wireless channel. As a result, users undergo a flat fading. The notations are summarized in
Table 2.
According to the definition of
Table 1, based on Shannon theorem, the corresponding data rate of FU
m over subcarrier
k is formulated as
where the
denotes subcarrier assignment of FU
m on subcarrier
k, which can only be either 1 or 0, indicating whether the subcarrier
k is used by the FU
m or not.
Due to the limitation of battery capacity of the
mth FU transmitter, the transmit power of each FU is not infinite, and the constraint is denoted by
where
is the maximum transmit power of FU
m.
Meanwhile, data rate should satisfy a minimum requirement to protect the QoS of FU
m, given by
where
denotes minimum rate requirement of FU
m.
The total cross-tier interference constraint from femtocell networks to MU receiver can be expressed as
where
is the interference temperature level at MU-receiver.
The sum rate maximization based Power Allocation (PA) problem for HetNets can be written as
ensures that each subcarrier
k is only assigned to one FU, where
means that the
kth subcarrier is used by FU
m. Moreover,
represents the transmission power constraint of FU
m over subcarriers.
can ensure the QoS of each FU.
denotes the total interference power to the MU receiver. The problem with integer variable
is a non-convex and mixed integer programming problem. Assume that the MU can provide the information of channel gains
feedback to the FU, which means that channel gains can be accurately estimated by FUs. Most of current power allocation in HetNets focus on optimal power control under perfect CSI [
22,
23].
In practice, however, channel uncertainties are inevitable due to estimation errors and quantization errors which cause harmful interference to the MUs [
24]. To reduce performance degradation of MUs, PA with channel uncertainties should be considered in advance. However, to the best of our knowledge, robust PA considering the QoS of both FUs and MUs has not been investigated in the existing works.
3. Robust Power Allocation Problem
Due to lack of cooperation between femtocell network and macrocell network, it is a difficult task to precisely estimate the channel gain
from FU-transmitter to MU-receiver. In this paper, our goal is to design a robust PA and subcarrier assignment scheme to ensure the communication quality of FUs and MUs under channel uncertainties. Hence, we reformulated the constraints
and
as probability form. The PA Problem (
5) with outage probability constraints is formulated as
where both of
and
ensure that the QoS of MU and FU are satisfied with a certain probability of outage event that is less than the outage probability threshold
and
, respectively. In general, Problem (
6) is a challenging optimization problem for obtaining analytical solutions because probabilistic rate and interference constraints (i.e.,
and
) are intractable and are not convex. The key step in the development of a tractable robust PA algorithm is to transform the outage probability constraints into efficiently-computable representation (e.g., convex form).
In the following part, we will transform the outage probability constraints into the deterministic and convex ones under imperfect statistical distribution model of uncertain parameter and perfect probability distributions of channel estimation errors.
3.1. Transformation without Statistical Information
In this section, the probabilistic interference constraint and probabilistic rate constraint are converted into the deterministic ones.
Due to the feature of OFDM technology, there is no mutual interference among different subcarriers, so that the data of each FU is mutually independent for all subcarriers. Define the rate set
and
According to the above definition, the set
is a subset of the intersection of
, i.e.,
According to probability theory, we have the following relationship,
If the upper bound of probabilistic rate constraint satisfies the outage probability requirement, based on the worst-case method, as we know, the stochastic constraint
is satisfied. Therefore, we have
From (
12), we have the deterministic form of outage-based probability constraint
, i.e.,
If transmission power of SU satisfies the constraint (
13), the outage probability of
can be ensured. The proof of (
13) is given in
Appendix A.
Similarly, the probabilistic interference constraint
can be transformed as
Therefore, the outage probability constraint
becomes a deterministic one. To keep the presentation concise, the proof of (
14) is given in
Appendix B.
Based on (
13) and (
14), the PA problem without knowledge of statistical model is given as
Obviously, problem (
6) becomes a deterministic one. If the inverse cumulative distribution functions (CDFs) of variables (e.g.,
and
) are well-known (i.e.,
and
), the problem (
15) can be easily solved. For example, if the channel gains are follow Rayleigh fading models, the problem can be well solved. In real communication scenario, however, due to the mobility of UEs, it is impractical to assume same fading models during different environments. Therefore, it is necessary to find a general method to solve this problem.
3.2. Transformation with Perfect Statistical Model
In order to address the above problem, it is feasible to find the solution with knowledge of perturbation part of uncertain channel gains.
If there are some errors in the estimated channel gain from feedback quantization or channel estimation [
25]. Channel uncertainties can be formulated as an additive model of uncertain parameter [
11], i.e.,
where
is the estimated channel gain between FU-transmitter and MU-receiver. And
denotes the estimated channel gains from FUs to their BS. Those parameters are perfectly known for FUs.
and
are the corresponding perturbation terms (i.e., estimation error).
It is clear that FUs can obtain the CSI by estimating the channels between FUs and MUs so that the causes of CSI errors are from channel estimation, as a result, this type of estimation error can be formulated as independent Gaussian distribution model [
25]. Therefore, uncertain parameter
is reasonably assumed to be distributed random with zero-mean and variance
, i.e.,
. However, the elements
in (
16) should be assumed to follow the independent uniform distributed random variables, i.e.,
, where
denotes the upper bound of uncertain region. The reason is that the uplink channel gain from FU’s transmitter to the BS is obtained by a quantizer to quantize CSI and feed it back to its corresponding FU’s transmitter.
To protect the performance of MUs, each FU transmits less power for avoiding harmful interference to the MU over link
k. Based on
and Model (
16), we have
where
denotes the subcarrier set of FU
m, and
represents the number of subcarrier that is chosen by FU
m. And
.
Due to uniform distribution of channel errors
, we have
and
As a result, the probabilistic rate constraint becomes a deterministic one as form of (
19).
According to the relationship of (
16) and constraint
, we have
where
is a deterministic term for FU’s transmitter. The Constraint (
20) can also be reformulated as
To satisfy the outage probability requirement, the interference constraint of left side in (
21) must hold under any channel estimation error.
Based on worst-case principle, we have
where
denotes the worst interference link between FU and MU.
denotes the number of element in set.
In other words, if the outage-based constraint can be ensured under the case of worst errors over all subcarriers, the outage performance of MU must be kept. Consequently, we have
Define
and
. Since there is
, the variable
follows the Gaussian distribution with zero mean and variance
, i.e.,
. As a result, we have
Since the sum of Gaussian random variable
is still obeying Gaussian distribution, i.e.,
and
, therefore, the expression of (
24) can be reformulated as
where
is a Gaussian Q-function with the expression of
. As a result, we have
where
denotes the inverse Gaussian Q-function. Combining with the inequality relationship
, we can use the upper bound of right side in (26) to obtain the decomposable form, i.e.,
As a result, the outage-based probability constraint
C6 becomes a deterministic form
Define
, combining (
6), (
19) and (
28), we obtain the considerable robust resource allocation problem as follows
As a result, the probabilistic optimization problem (
6) is transformed into a non-probabilistic one (
29).
4. Robust Resource Allocation Algorithm
Obviously, Problem (
29) is still not a convex problem due to the integer variable
. Since both the real variable
and integer variable
are in the optimization problem, it conducts a mixed integer programming problem. Thus, we relax the subcarrier assignment factor into continuous one and introduce a variable
for any FU and subcarrier, where
indicates a time-division multiple access (TDMA) strategy for different FUs. Therefore, the Problem (
29) becomes a convex optimization problem as follows,
where
denotes the effective data rate due to unknown channel gain
(i.e., true physical channel gain). The objective function in (
30) is concave since the corresponding hessian matrix can be proved to be negative semi-definiteness by using the Lemma 1 in [
26]. In addition, the constraints are linear so that the robust optimization Problem (
30) is a convex problem.
We can obtain the analytical solutions by using Lagrangian methods [
27]. To deal with the optimization problem (
30), we first define a Lagrangian function as
where
,
,
and
are the nonnegative Lagrangian multipliers for the corresponding constraints in (
30), respectively. The Lagrangian dual function can be defined as
And the dual problem is formulated as
The Lagrangian dual Problems (
32) and (
33) can be decomposed into a master problem and
subproblems [
27]. As a result, the Lagrangian function can be rewritten as
where
The Karush-Kuhn-Tucker (KKT) conditions of variables
and
can be obtained by calculating the derivatives of (35) with the optimal variables, i.e.,
where ⊥ denotes the orthogonality relationship of the corresponding variables. Additionally, the derivatives
and
are given as
As a result, according to KKT conditions, we obtain the optimal transmit power
where
. Moreover, the subcarrier
k is assigned to the optimal user
, i.e.,
where
The Lagrangian multipliers can be updated as follows
where
t denotes the iteration number.
,
and
are the corresponding small step sizes. When the step sizes are sufficiently small, Lagrange multipliers can converge to equilibrium points [
28]. The implementation procedure of the algorithm is given in Algorithm 1 and the algorithm flow chart is shown in
Figure 2.
| Algorithm 1: The implementation procedure. |
- 1:
Initialize maximum iteration number ; Set: iterations , , ; Lagrangian multipliers , , and ; Outage probability thresholds , ; Upper bound of channel estimation error in FU’s link is ; Variance of estimation error in FU-to-MU link is ; - 2:
Set maximum transmit power and initialize power with same initialization values among all subcarriers. Define interference , randomly generate and . - 3:
Initialize with subcarrier assignment method in [ 29], group subcarrier set and calculate . - 4:
repeat - 5:
for to do - 6:
for to M do - 7:
for to K do - 8:
Calculate transmit power according to ( 40) - 9:
Calculate by ( 42) - 10:
Calculate by using ( 41) - 11:
Calculate Lagrange multipliers , , and from ( 43– 45) - 12:
end for - 13:
end for - 14:
- 15:
end for - 16:
until or transmit power convergence
|