The Heading Weight Function: A Novel LiDAR-Based Local Planner for Nonholonomic Mobile Robots
Abstract
:1. Introduction
2. Methods
2.1. Mobile Robot Kinematics
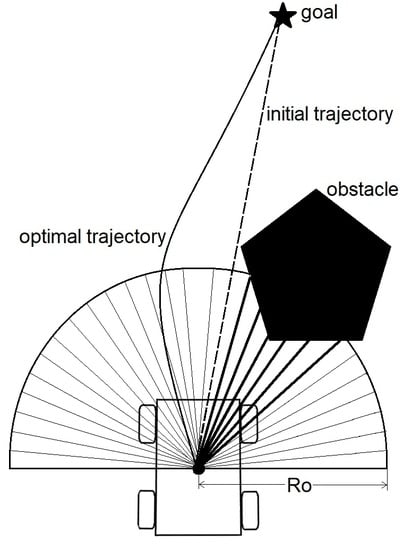
2.2. The Heading Weight Function
3. Results
3.1. Simulation Results
The Case of Nonsatisfaction of the FST Condition
3.2. Experimental Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fox, D.; Burgard, W.; Thrun, S. The dynamic window approach to collision avoidance. IEEE Rob. Autom Mag. 1997, 4, 23–33. [Google Scholar] [CrossRef]
- Brock, O.; Khatib, O. High-speed navigation using the global dynamic window approach. In Proceedings of the 1999 IEEE International Conference on Robotics and Automation, Detroit, MI, USA, 10–15 May 1999. [Google Scholar]
- Lumelsky, V.J.; Skewis, T. Incorporating range sensing in the robot navigation function. IEEE Trans. Syst. Man Cybern. 1990, 20, 1058–1069. [Google Scholar] [CrossRef] [Green Version]
- Kamon, I.; Rivlin, E.; Rimon, E. A new range-sensor based globally convergent navigation algorithm for mobile robots. In Proceedings of the IEEE International Conference on Robotics and Automation, Minneapolis, MN, USA, 22–28 April 1996. [Google Scholar]
- Siegwart, R.; Nourbakhsh, I.R.; Scaramuzza, D.; Arkin, R.C. Introduction to Autonomous Mobile Robots; MIT Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Borenstein, J.; Koren, Y. The vector field histogram-fast obstacle avoidance for mobile robots. IEEE Trans. Rob. Autom. 1991, 7, 278–288. [Google Scholar] [CrossRef] [Green Version]
- Bertozzi, M.; Broggi, A. GOLD: A parallel real-time stereo vision system for generic obstacle and lane detection. IEEE Trans. Image Process. 1998, 7, 62–81. [Google Scholar] [CrossRef] [PubMed]
- Holz, D.; Holzer, S.; Rusu, R.B.; Behnke, S. Real-time plane segmentation using RGB-D cameras. In Robot Soccer World Cup; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Sabatini, R.; Gardi, A.; Richardson, M. LIDAR obstacle warning and avoidance system for unmanned aircraft. Int. J. Mech. Aerosp. Ind. Mechatron. Eng. 2014, 8, 718–729. [Google Scholar]
- Michels, J.; Saxena, A.; Ng, A.Y. High speed obstacle avoidance using monocular vision and reinforcement learning. In Proceedings of the 22nd International Conference on Machine Learning, Bonn, Germany, 7–11 August 2005. [Google Scholar]
- Nguyen, V.; Gächter, S.; Martinelli, A.; Tomatis, N.; Siegwart, R. A comparison of line extraction algorithms using 2D range data for indoor mobile robotics. Auton. Robots 2007, 23, 97–111. [Google Scholar] [CrossRef] [Green Version]
- Pang, C.; Zhong, X.; Hu, H.; Tian, J.; Peng, X.; Zeng, J. Adaptive obstacle detection for mobile robots in urban environments using downward-looking 2D LiDAR. Sensors 2018, 18, 1749. [Google Scholar] [CrossRef] [PubMed]
- Peng, Y.; Qu, D.; Zhong, Y.; Xie, S.; Luo, J.; Gu, J. The obstacle detection and obstacle avoidance algorithm based on 2-d lidar. In Proceedings of the 2015 IEEE International Conference on Information and Automation, Lijiang, China, 8–10 August 2015. [Google Scholar]
- Lundell, J.; Verdoja, F.; Kyrki, V. Hallucinating robots: Inferring obstacle distances from partial laser measurements. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018. [Google Scholar]
- Wu, P.; Xie, S.; Liu, H.; Luo, J.; Li, Q. A novel algorithm of autonomous obstacle-avoidance for mobile robot based on lidar data. In Proceedings of the 2015 IEEE International Conference on Robotics and Biomimetics (ROBIO), Zhuhai, China, 6–9 December 2015. [Google Scholar]
- Takahashi, M.; Kobayashi, K.; Watanabe, K.; Kinoshita, T. Development of prediction based emergency obstacle avoidance module by using LIDAR for mobile robot. In Proceedings of the 2014 Joint 7th International Conference on Soft Computing and Intelligent Systems (SCIS) and 15th International Symposium on Advanced Intelligent Systems (ISIS), Kitakyushu, Japan, 3–6 December 2014. [Google Scholar]
- Padgett, S.T.; Browne, A.F. Vector-based robot obstacle avoidance using LIDAR and mecanum drive. In Proceedings of the SoutheastCon, Charlotte, NC, USA, 30 March–2 April 2017. [Google Scholar]
- Harik, E.H.C.; Guérin, F.; Guinand, F.; Brethé, J.-F.; Pelvillain, H. UAV-UGV cooperation for objects transportation in an industrial area. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015. [Google Scholar]
- EHarik, H.C.; Korsaeth, A. Combining Hector SLAM and Artificial Potential Field for Autonomous Navigation Inside a Greenhouse. Robotics 2018, 7, 22. [Google Scholar] [Green Version]
- Gazebo, Gazebosim, 2019. Available online: http://gazebosim.org/ (accessed on 7 June 2019).
- ROS, Robot Operating System, 2019. Available online: http://www.ros.org/ (accessed on 7 June 2019).
- Marvelmind, Marvelmind Robotics. Available online: https://marvelmind.com/ (accessed on 7 June 2019).
















| Parameter | Significance | Value |
|---|---|---|
| Initial x position of the robot in the global frame | 1.92 m | |
| Initial y position of the robot in the global frame | 6.93 m | |
| Initial orientation of the robot in the global frame | −2.84 rad | |
| Distance tolerance to the waypoint | 0.3 m | |
| Positive gain for the linear velocity | 0.4 | |
| Positive gain for the angular velocity | 1.8 | |
| Positive gain 1 for the HWF | 0.01 | |
| Positive gain 2 for the HWF | 0.04 | |
| Obstacle threshold radius | 1.2 m | |
| LiDAR resolution | 0.004914 rad | |
| Predefined angle of the FST | 0.5838 rad | |
| Positive gain for the HWF | 5.0 |
| Parameter | Significance | Value |
|---|---|---|
| Initial x position of the robot in the global frame | 0.08 m | |
| Initial y position of the robot in the global frame | 7.18 m | |
| x position of the parking location in the global frame | −0.5 m | |
| y position of the parking location in the global frame | 1.92 m | |
| Initial orientation of the robot in the global frame | −0.08 rad | |
| Distance tolerance to the waypoint | 0.15 m | |
| Positive gain for the linear velocity | 0.5 | |
| Positive gain for the angular velocity | 2.2 | |
| Positive gain 1 for the HWF | 0.001 | |
| Positive gain 2 for the HWF | 0.04 | |
| Obstacle threshold radius | 0.95 m | |
| LiDAR resolution | 0.005817 rad | |
| Predefined angle of the FST | 0.5838 rad | |
| Positive gain for the HWF | 1.2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harik, E.H.C.; Korsaeth, A. The Heading Weight Function: A Novel LiDAR-Based Local Planner for Nonholonomic Mobile Robots. Sensors 2019, 19, 3606. https://doi.org/10.3390/s19163606
Harik EHC, Korsaeth A. The Heading Weight Function: A Novel LiDAR-Based Local Planner for Nonholonomic Mobile Robots. Sensors. 2019; 19(16):3606. https://doi.org/10.3390/s19163606
Chicago/Turabian StyleHarik, El Houssein Chouaib, and Audun Korsaeth. 2019. "The Heading Weight Function: A Novel LiDAR-Based Local Planner for Nonholonomic Mobile Robots" Sensors 19, no. 16: 3606. https://doi.org/10.3390/s19163606
APA StyleHarik, E. H. C., & Korsaeth, A. (2019). The Heading Weight Function: A Novel LiDAR-Based Local Planner for Nonholonomic Mobile Robots. Sensors, 19(16), 3606. https://doi.org/10.3390/s19163606