A Fast Linearly Wavelength Step-Swept Light Source Based on Recirculating Frequency Shifter and Its Application to FBG Sensor Interrogation
Abstract
:1. Introduction
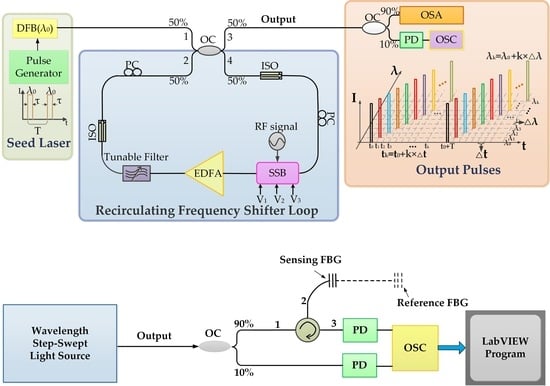
2. Experimental Setup and the Performance of WSSL
3. Wavelength Interrogation of FBG Based on the WSSL
3.1. Wavelength Interrogation of Static Strain and Temperature Sensing
3.2. Wavelength Interrogation of Dynamic Strain Sensing
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kersey, A.D.; Davis, M.A.; Patrick, H.J.; LeBlanc, M.; Koo, K.P.; Askins, C.G.; Putnam, M.A.; Friebele, E.J. Fiber grating sensors. J. Lightw. Technol. 1997, 15, 1442–1463. [Google Scholar] [CrossRef]
- Rao, Y.J. In-fibre Bragg grating sensors. Meas. Sci. Technol. 1997, 8, 355–375. [Google Scholar] [CrossRef]
- Campanella, C.E.; Cuccovillo, A.; Campanella, C.; Yurt, A.; Passaro, V.M.N. Fibre Bragg Grating Based Strain Sensors: Review of Technology and Applications. Sensors 2018, 18, 3115. [Google Scholar] [CrossRef] [PubMed]
- Lee, B. Review of the present status of optical fiber sensors. Opt. Fiber Technol. 2003, 9, 57–79. [Google Scholar] [CrossRef]
- Hill, K.O.; Meltz, G. Fiber Bragg Grating Technology Fundamentals and Overview. J. Lightw. Technol. 1997, 15, 1263–1276. [Google Scholar] [CrossRef]
- Kersey, A.D.; Berkoff, T.A.; Morey, W.W. High-Resolution Fiber-Grating Based Strain Sensor with Interferometric Wavelength-Shift Detection. Electron. Lett. 1992, 28, 236–238. [Google Scholar] [CrossRef]
- Melle, S.M.; Liu, K.; Measures, R.M. A Passive Wavelength Demodulation System for Guided-Wave Bragg Grating Sensors. IEEE Photonics Technol. Lett. 1992, 4, 516–518. [Google Scholar] [CrossRef]
- Xiao, G.Z.; Zhao, P.; Sun, F.G.; Lu, Z.G.; Zhang, Z.; Grover, C.P. Interrogating fiber Bragg grating sensors by thermally scanning a demultiplexer based on arrayed waveguide gratings. Opt. Lett. 2004, 29, 2222–2224. [Google Scholar] [CrossRef] [PubMed]
- Lobo Ribeiro, A.B.; Ferreira, L.A.; Tsvetkov, M.; Santos, J.L. All-fibre interrogation technique for fibre Bragg sensors using a biconical fibre filter. Electron. Lett. 1996, 32, 382–383. [Google Scholar] [CrossRef]
- Arie, A.; Lissak, B.; Tur, M. Static Fiber-Bragg Grating Strain Sensing Using Frequency-Locked Lasers. J. Lightw. Technol. 1999, 17, 1849–1855. [Google Scholar] [CrossRef]
- Davis, M.A.; Kersey, A.D. All-fibre Bragg grating strain-sensor demodulation technique using a wavelength division coupler. Electron. Lett. 1994, 30, 75–77. [Google Scholar] [CrossRef]
- Yu, S.H.; Richardson, D.J.; Kim, B.Y. Interrogation of fiber grating sensor arrays with a wavelength-swept fiber laser. Opt. Lett. 1998, 23, 843–845. [Google Scholar]
- Ryu, C.Y.; Hong, C.S. Development of fiber Bragg grating sensor system using wavelength-swept fiber laser. Smart Mater. Struct. 2002, 11, 468–473. [Google Scholar] [CrossRef]
- Wang, Y.; Cui, Y.; Yun, B. A Fiber Bragg Grating Sensor System for Simultaneously Static and Dynamic Measurements with a Wavelength-Swept Fiber Laser. IEEE Photonics Technol. Lett. 2006, 18, 1539–1541. [Google Scholar] [CrossRef]
- Lin, G.R.; Chang, J.Y.; Liao, Y.S.; Lu, H.H. L-band Erbium-doped fiber laser with coupling ratio controlled wavelength tenability. Opt. Express 2006, 14, 9743–9749. [Google Scholar] [CrossRef] [PubMed]
- Kwon, Y.S.; Ko, M.O.; Jung, M.S.; Park, I.G.; Kim, N.; Han, S.P.; Ryu, H.C.; Park, K.H.; Jeon, M.Y. Dynamic Sensor Interrogation Using Wavelength-Swept Laser with a Polygon-Scanner-Based Wavelength Filter. Sensors 2013, 13, 9669–9678. [Google Scholar] [CrossRef] [Green Version]
- Jung, E.J.; Kim, C.S.; Jeong, M.Y.; Kim, M.K.; Jeon, M.Y.; Jung, W.; Chen, Z. Characterization of FBG sensor interrogation based on a FDML wavelength swept laser. Opt. Express 2008, 16, 16552–16560. [Google Scholar]
- Lee, H.D.; Jung, E.J.; Jeong, M.Y.; Chen, Z.; Kim, C.S. Uniform spacing interrogation of a Fourier domain mode-locked fiber Bragg grating sensor system using a polarization-maintaining fiber Sagnac interferometer. Meas. Sci. Technol. 2013, 24, 065101. [Google Scholar] [CrossRef] [Green Version]
- Nakazaki, Y.; Yamashita, S. Fast and wide tuning range wavelength-swept fiber laser based on dispersion tuning and its application to dynamic FBG sensing. Opt. Express 2009, 17, 8310–8318. [Google Scholar] [CrossRef]
- Lee, H.D.; Kim, G.H.; Eom, T.J.; Jeong, M.Y.; Kim, C.S. Linearized Wavelength Interrogation System of Fiber Bragg Grating Strain Sensor Based on Wavelength-Swept Active Mode Locking Fiber Laser. J. Lightw. Technol. 2015, 33, 2617–2622. [Google Scholar] [CrossRef]
- Huang, Y.H.; Lu, C.; Wai, P.K.A.; Tam, H.Y. Fast FBG Sensor Interrogation System Using Vertical Cavity Surface Emitting Laser Source. In Proceedings of the 14th OptoElectronics and Communications Conference, Hong Kong, China, 13–17 July 2009. [Google Scholar]
- Njegovec, M.; Donlagic, D. Interrogation of FBGs and FBGs Arrays Using Standard Telecom DFB Diode. J. Lightw. Technol. 2016, 34, 5340–5348. [Google Scholar] [CrossRef]
- Lee, H.S.; Lee, H.D.; Kim, H.J.; Cho, J.D.; Jeong, M.Y.; Kim, C.S. A Fiber Bragg Grating Sensor Interrogation System Based on a Linearly Wavelength-Swept Thermo-Optic Laser Chip. Sensors 2014, 14, 16109–16116. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, W.; Zhang, W.; Li, F. Swept optical SSB-SC modulation technique for high-resolution large-dynamic-range static strain measurement using FBG-FP sensors. Opt. Lett. 2015, 40, 1406–1409. [Google Scholar] [CrossRef]
- Shimizu, K.; Horiguchi, T.; Koyamada, Y. Frequency translation of light waves by propagation around an optical ring circuit containing a frequency shifter: I. Experiment. Appl. Opt. 1993, 32, 6718–6726. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, K.; Horiguchi, T.; Koyamada, Y. Frequency translation of light waves by propagation around an optical ring circuit containing a frequency shifter: II. Theoretical analysis. Appl. Opt. 1994, 33, 3209–3219. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Liu, S.; Luo, S.; Yuan, Q.; Ma, R.; Ge, C.; Yang, T. Broadband lightwave synthesized frequency sweeper using self-induced auto-tracking filter. Opt. Express 2015, 23, 22134–22140. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Qin, X.; Gao, C.; Wang, T.; Jia, D.; Sang, M.; Yang, T. Precise Simultaneous Multiwavelength Tuning by Electrical RF Signals. IEEE Photonics Technol. Lett. 2013, 25, 914–916. [Google Scholar] [CrossRef]
- Lu, Z.; Yang, T.; Li, Z.; Guo, C.; Wang, Z.; Jia, D.; Ge, C. Broadband linearly chirped light source with narrow linewidth based on external modulation. Opt. Lett. 2018, 43, 4144–4147. [Google Scholar] [CrossRef] [PubMed]












© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, Q.; Wang, Z.; Song, L.; Lu, Z.; Hu, D.; Qin, J.; Yang, T. A Fast Linearly Wavelength Step-Swept Light Source Based on Recirculating Frequency Shifter and Its Application to FBG Sensor Interrogation. Sensors 2019, 19, 593. https://doi.org/10.3390/s19030593
Yuan Q, Wang Z, Song L, Lu Z, Hu D, Qin J, Yang T. A Fast Linearly Wavelength Step-Swept Light Source Based on Recirculating Frequency Shifter and Its Application to FBG Sensor Interrogation. Sensors. 2019; 19(3):593. https://doi.org/10.3390/s19030593
Chicago/Turabian StyleYuan, Quan, Zhaoying Wang, Lipei Song, Zhaoyu Lu, Diannan Hu, Jiaqi Qin, and Tianxin Yang. 2019. "A Fast Linearly Wavelength Step-Swept Light Source Based on Recirculating Frequency Shifter and Its Application to FBG Sensor Interrogation" Sensors 19, no. 3: 593. https://doi.org/10.3390/s19030593
APA StyleYuan, Q., Wang, Z., Song, L., Lu, Z., Hu, D., Qin, J., & Yang, T. (2019). A Fast Linearly Wavelength Step-Swept Light Source Based on Recirculating Frequency Shifter and Its Application to FBG Sensor Interrogation. Sensors, 19(3), 593. https://doi.org/10.3390/s19030593