Continuous-Flow Separation of Magnetic Particles from Biofluids: How Does the Microdevice Geometry Determine the Separation Performance?
Abstract
:1. Introduction
2. Theoretical Methods
2.1. CFD Model
2.2. Geometric Configurations and Simulation Setup
2.3. Dimensionless Analysis
3. Results and Discussion
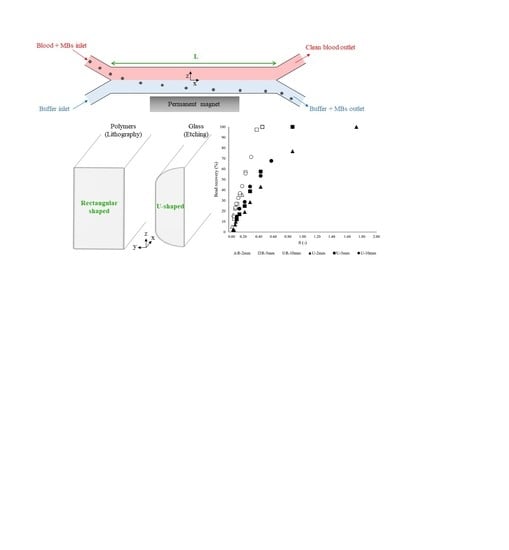
3.1. Influence of Microchannel Cross Section Shape
3.2. Influence of Microchannel Length
3.3. Dimensionless Channel Design
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Gómez-Pastora, J.; Xue, X.; Karampelas, I.H.; Bringas, E.; Furlani, E.P.; Ortiz, I. Analysis of separators for magnetic beads recovery: From large systems to multifunctional microdevices. Sep. Purif. Technol. 2017, 172, 16–31. [Google Scholar] [CrossRef]
- Wise, N.; Grob, T.; Morten, K.; Thompson, I.; Sheard, S. Magnetophoretic velocities of superparamagnetic particles, agglomerates and complexes. J. Magn. Magn. Mater. 2015, 384, 328–334. [Google Scholar] [CrossRef]
- Khashan, S.A.; Elnajjar, E.; Haik, Y. CFD simulation of the magnetophoretic separation in a microchannel. J. Magn. Magn. Mater. 2011, 323, 2960–2967. [Google Scholar] [CrossRef]
- Khashan, S.A.; Furlani, E.P. Scalability analysis of magnetic bead separation in a microchannel with an array of soft magnetic elements in a uniform magnetic field. Sep. Purif. Technol. 2014, 125, 311–318. [Google Scholar] [CrossRef]
- Furlani, E.P. Magnetic biotransport: Analysis and applications. Materials 2010, 3, 2412–2446. [Google Scholar] [CrossRef] [Green Version]
- Gómez-Pastora, J.; Bringas, E.; Ortiz, I. Design of novel adsorption processes for the removal of arsenic from polluted groundwater employing functionalized magnetic nanoparticles. Chem. Eng. Trans. 2016, 47, 241–246. [Google Scholar]
- Gómez-Pastora, J.; Bringas, E.; Lázaro-Díez, M.; Ramos-Vivas, J.; Ortiz, I. The reverse of controlled release: Controlled sequestration of species and biotoxins into nanoparticles (NPs). In Drug Delivery Systems; Stroeve, P., Mahmoudi, M., Eds.; World Scientific: Hackensack, NJ, USA, 2017; pp. 207–244. ISBN 9789813201057. [Google Scholar]
- Ruffert, C. Magnetic bead-magic bullet. Micromachines 2016, 7, 21. [Google Scholar] [CrossRef] [Green Version]
- Yáñez-Sedeño, P.; Campuzano, S.; Pingarrón, J.M. Magnetic particles coupled to disposable screen printed transducers for electrochemical biosensing. Sensors 2016, 16, 1585. [Google Scholar] [CrossRef] [Green Version]
- Schrittwieser, S.; Pelaz, B.; Parak, W.J.; Lentijo-Mozo, S.; Soulantica, K.; Dieckhoff, J.; Ludwig, F.; Guenther, A.; Tschöpe, A.; Schotter, J. Homogeneous biosensing based on magnetic particle labels. Sensors 2016, 16, 828. [Google Scholar] [CrossRef] [Green Version]
- He, J.; Huang, M.; Wang, D.; Zhang, Z.; Li, G. Magnetic separation techniques in sample preparation for biological analysis: A review. J. Pharm. Biomed. Anal. 2014, 101, 84–101. [Google Scholar] [CrossRef]
- Ha, Y.; Ko, S.; Kim, I.; Huang, Y.; Mohanty, K.; Huh, C.; Maynard, J.A. Recent advances incorporating superparamagnetic nanoparticles into immunoassays. ACS Appl. Nano Mater. 2018, 1, 512–521. [Google Scholar] [CrossRef] [Green Version]
- Gómez-Pastora, J.; González-Fernández, C.; Fallanza, M.; Bringas, E.; Ortiz, I. Flow patterns and mass transfer performance of miscible liquid-liquid flows in various microchannels: Numerical and experimental studies. Chem. Eng. J. 2018, 344, 487–497. [Google Scholar] [CrossRef]
- Gale, B.K.; Jafek, A.R.; Lambert, C.J.; Goenner, B.L.; Moghimifam, H.; Nze, U.C.; Kamarapu, S.K. A review of current methods in microfluidic device fabrication and future commercialization prospects. Inventions 2018, 3, 60. [Google Scholar] [CrossRef] [Green Version]
- Nanobiotechnology; Concepts, Applications and Perspectives; Niemeyer, C.M.; Mirkin, C.A. (Eds.) Wiley-VCH: Weinheim, Germany, 2004; ISBN 3527305068. [Google Scholar]
- Khashan, S.A.; Dagher, S.; Alazzam, A.; Mathew, B.; Hilal-Alnaqbi, A. Microdevice for continuous flow magnetic separation for bioengineering applications. J. Micromech. Microeng. 2017, 27, 055016. [Google Scholar] [CrossRef] [Green Version]
- Basauri, A.; Gomez-Pastora, J.; Fallanza, M.; Bringas, E.; Ortiz, I. Predictive model for the design of reactive micro-separations. Sep. Purif. Technol. 2019, 209, 900–907. [Google Scholar] [CrossRef]
- Abdollahi, P.; Karimi-Sabet, J.; Moosavian, M.A.; Amini, Y. Microfluidic solvent extraction of calcium: Modeling and optimization of the process variables. Sep. Purif. Technol. 2020, 231, 115875. [Google Scholar] [CrossRef]
- Khashan, S.A.; Alazzam, A.; Furlani, E. A novel design for a microfluidic magnetophoresis system: Computational study. In Proceedings of the 12th International Symposium on Fluid Control, Measurement and Visualization (FLUCOME2013), Nara, Japan, 18–23 November 2013. [Google Scholar]
- Pamme, N. Magnetism and microfluidics. Lab Chip 2006, 6, 24–38. [Google Scholar] [CrossRef]
- Gómez-Pastora, J.; Amiri Roodan, V.; Karampelas, I.H.; Alorabi, A.Q.; Tarn, M.D.; Iles, A.; Bringas, E.; Paunov, V.N.; Pamme, N.; Furlani, E.P.; et al. Two-step numerical approach to predict ferrofluid droplet generation and manipulation inside multilaminar flow chambers. J. Phys. Chem. C 2019, 123, 10065–10080. [Google Scholar] [CrossRef]
- Gómez-Pastora, J.; Karampelas, I.H.; Bringas, E.; Furlani, E.P.; Ortiz, I. Numerical analysis of bead magnetophoresis from flowing blood in a continuous-flow microchannel: Implications to the bead-fluid interactions. Sci. Rep. 2019, 9, 7265. [Google Scholar] [CrossRef] [Green Version]
- Tarn, M.D.; Pamme, N. On-Chip Magnetic Particle-Based Immunoassays Using Multilaminar Flow for Clinical Diagnostics. In Microchip Diagnostics Methods and Protocols; Taly, V., Viovy, J.L., Descroix, S., Eds.; Humana Press: New York, NY, USA, 2017; pp. 69–83. [Google Scholar]
- Phurimsak, C.; Tarn, M.D.; Peyman, S.A.; Greenman, J.; Pamme, N. On-chip determination of c-reactive protein using magnetic particles in continuous flow. Anal. Chem. 2014, 86, 10552–10559. [Google Scholar] [CrossRef]
- Wu, X.; Wu, H.; Hu, Y. Enhancement of separation efficiency on continuous magnetophoresis by utilizing L/T-shaped microchannels. Microfluid. Nanofluid. 2011, 11, 11–24. [Google Scholar] [CrossRef]
- Vojtíšek, M.; Tarn, M.D.; Hirota, N.; Pamme, N. Microfluidic devices in superconducting magnets: On-chip free-flow diamagnetophoresis of polymer particles and bubbles. Microfluid. Nanofluid. 2012, 13, 625–635. [Google Scholar] [CrossRef]
- Gómez-Pastora, J.; González-Fernández, C.; Real, E.; Iles, A.; Bringas, E.; Furlani, E.P.; Ortiz, I. Computational modeling and fluorescence microscopy characterization of a two-phase magnetophoretic microsystem for continuous-flow blood detoxification. Lab Chip 2018, 18, 1593–1606. [Google Scholar] [CrossRef] [PubMed]
- Forbes, T.P.; Forry, S.P. Microfluidic magnetophoretic separations of immunomagnetically labeled rare mammalian cells. Lab Chip 2012, 12, 1471–1479. [Google Scholar] [CrossRef]
- Nandy, K.; Chaudhuri, S.; Ganguly, R.; Puri, I.K. Analytical model for the magnetophoretic capture of magnetic microspheres in microfluidic devices. J. Magn. Magn. Mater. 2008, 320, 1398–1405. [Google Scholar] [CrossRef]
- Plouffe, B.D.; Lewis, L.H.; Murthy, S.K. Computational design optimization for microfluidic magnetophoresis. Biomicrofluidics 2011, 5, 013413. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hale, C.; Darabi, J. Magnetophoretic-based microfluidic device for DNA isolation. Biomicrofluidics 2014, 8, 044118. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Becker, H.; Gärtner, C. Polymer microfabrication methods for microfluidic analytical applications. Electrophoresis 2000, 21, 12–26. [Google Scholar] [CrossRef]
- Pekas, N.; Zhang, Q.; Nannini, M.; Juncker, D. Wet-etching of structures with straight facets and adjustable taper into glass substrates. Lab Chip 2010, 10, 494–498. [Google Scholar] [CrossRef]
- Wang, T.; Chen, J.; Zhou, T.; Song, L. Fabricating microstructures on glass for microfluidic chips by glass molding process. Micromachines 2018, 9, 269. [Google Scholar] [CrossRef] [Green Version]
- Castaño-Álvarez, M.; Pozo Ayuso, D.F.; García Granda, M.; Fernández-Abedul, M.T.; Rodríguez García, J.; Costa-García, A. Critical points in the fabrication of microfluidic devices on glass substrates. Sens. Actuators B Chem. 2008, 130, 436–448. [Google Scholar] [CrossRef]
- Prakash, S.; Kumar, S. Fabrication of microchannels: A review. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2015, 229, 1273–1288. [Google Scholar] [CrossRef]
- Leester-Schädel, M.; Lorenz, T.; Jürgens, F.; Ritcher, C. Fabrication of Microfluidic Devices. In Microsystems for Pharmatechnology: Manipulation of Fluids, Particles, Droplets, and Cells; Dietzel, A., Ed.; Springer: Basel, Switzerland, 2016; pp. 23–57. ISBN 9783319269207. [Google Scholar]
- Bartlett, N.W.; Wood, R.J. Comparative analysis of fabrication methods for achieving rounded microchannels in PDMS. J. Micromech. Microeng. 2016, 26, 115013. [Google Scholar] [CrossRef] [Green Version]
- Ng, P.F.; Lee, K.I.; Yang, M.; Fei, B. Fabrication of 3D PDMS microchannels of adjustable cross-sections via versatile gel templates. Polymers 2019, 11, 64. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Furlani, E.P.; Sahoo, Y.; Ng, K.C.; Wortman, J.C.; Monk, T.E. A model for predicting magnetic particle capture in a microfluidic bioseparator. Biomed. Microdevices 2007, 9, 451–463. [Google Scholar] [CrossRef] [Green Version]
- Tarn, M.D.; Peyman, S.A.; Robert, D.; Iles, A.; Wilhelm, C.; Pamme, N. The importance of particle type selection and temperature control for on-chip free-flow magnetophoresis. J. Magn. Magn. Mater. 2009, 321, 4115–4122. [Google Scholar] [CrossRef]
- Furlani, E.P. Permanent Magnet and Electromechanical Devices; Materials, Analysis and Applications; Academic Press: Waltham, MA, USA, 2001. [Google Scholar]
- White, F.M. Viscous Fluid Flow; McGraw-Hill: New York, NY, USA, 1974. [Google Scholar]
- Mathew, B.; Alazzam, A.; El-Khasawneh, B.; Maalouf, M.; Destgeer, G.; Sung, H.J. Model for tracing the path of microparticles in continuous flow microfluidic devices for 2D focusing via standing acoustic waves. Sep. Purif. Technol. 2015, 153, 99–107. [Google Scholar] [CrossRef]
- Furlani, E.J.; Furlani, E.P. A model for predicting magnetic targeting of multifunctional particles in the microvasculature. J. Magn. Magn. Mater. 2007, 312, 187–193. [Google Scholar] [CrossRef] [Green Version]
- Furlani, E.P.; Ng, K.C. Analytical model of magnetic nanoparticle transport and capture in the microvasculature. Phys. Rev. E 2006, 73, 061919. [Google Scholar] [CrossRef] [Green Version]
- Eibl, R.; Eibl, D.; Pörtner, R.; Catapano, G.; Czermak, P. Cell and Tissue Reaction Engineering; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Pamme, N.; Eijkel, J.C.T.; Manz, A. On-chip free-flow magnetophoresis: Separation and detection of mixtures of magnetic particles in continuous flow. J. Magn. Magn. Mater. 2006, 307, 237–244. [Google Scholar] [CrossRef]
- Alorabi, A.Q.; Tarn, M.D.; Gómez-Pastora, J.; Bringas, E.; Ortiz, I.; Paunov, V.N.; Pamme, N. On-chip polyelectrolyte coating onto magnetic droplets-Towards continuous flow assembly of drug delivery capsules. Lab Chip 2017, 17, 3785–3795. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Guo, H.; Chen, Z.; Zhang, G.; Li, Z. Application of PECVD SiC in glass micromachining. J. Micromech. Microeng. 2007, 17, 775–780. [Google Scholar] [CrossRef]
- Mourzina, Y.; Steffen, A.; Offenhäusser, A. The evaporated metal masks for chemical glass etching for BioMEMS. Microsyst. Technol. 2005, 11, 135–140. [Google Scholar] [CrossRef]
- Mata, A.; Fleischman, A.J.; Roy, S. Fabrication of multi-layer SU-8 microstructures. J. Micromech. Microeng. 2006, 16, 276–284. [Google Scholar] [CrossRef]
- Su, N. 8 2000 Negative Tone Photoresist Formulations 2002–2025; MicroChem Corporation: Newton, MA, USA, 2002. [Google Scholar]
- Su, N. 8 2000 Negative Tone Photoresist Formulations 2035–2100; MicroChem Corporation: Newton, MA, USA, 2002. [Google Scholar]
- Fu, C.; Hung, C.; Huang, H. A novel and simple fabrication method of embedded SU-8 micro channels by direct UV lithography. J. Phys. Conf. Ser. 2006, 34, 330–335. [Google Scholar] [CrossRef] [Green Version]
- Kazoe, Y.; Yamashiro, I.; Mawatari, K.; Kitamori, T. High-pressure acceleration of nanoliter droplets in the gas phase in a microchannel. Micromachines 2016, 7, 142. [Google Scholar] [CrossRef] [Green Version]
- Sharp, K.V.; Adrian, R.J.; Santiago, J.G.; Molho, J.I. Liquid flows in microchannels. In MEMS: Introduction and Fundamentals; Gad-el-Hak, M., Ed.; CRC Press: Boca Raton, FL, USA, 2006; pp. 10-1–10-46. ISBN 9781420036572. [Google Scholar]
- Oh, K.W.; Lee, K.; Ahn, B.; Furlani, E.P. Design of pressure-driven microfluidic networks using electric circuit analogy. Lab Chip 2012, 12, 515–545. [Google Scholar] [CrossRef]
- Bruus, H. Theoretical Microfluidics; Oxford University Press: New York, NY, USA, 2008; ISBN 9788578110796. [Google Scholar]
- Beebe, D.J.; Mensing, G.A.; Walker, G.M. Physics and applications of microfluidics in biology. Annu. Rev. Biomed. Eng. 2002, 4, 261–286. [Google Scholar] [CrossRef] [PubMed]
- Yalikun, Y.; Tanaka, Y. Large-scale integration of all-glass valves on a microfluidic device. Micromachines 2016, 7, 83. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Van Heeren, H.; Verhoeven, D.; Atkins, T.; Tzannis, A.; Becker, H.; Beusink, W.; Chen, P. Design Guideline for Microfluidic Device and Component Interfaces (Part 2), Version 3; Available online: http://www.makefluidics.com/en/design-guideline?id=7 (accessed on 9 March 2020).
- Scheuble, N.; Iles, A.; Wootton, R.C.R.; Windhab, E.J.; Fischer, P.; Elvira, K.S. Microfluidic technique for the simultaneous quantification of emulsion instabilities and lipid digestion kinetics. Anal. Chem. 2017, 89, 9116–9123. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lynch, E.C. Red blood cell damage by shear stress. Biophys. J. 1972, 12, 257–273. [Google Scholar]
- Paul, R.; Apel, J.; Klaus, S.; Schügner, F.; Schwindke, P.; Reul, H. Shear stress related blood damage in laminar Couette flow. Artif. Organs 2003, 27, 517–529. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Pastora, J.; Karampelas, I.H.; Xue, X.; Bringas, E.; Furlani, E.P.; Ortiz, I. Magnetic bead separation from flowing blood in a two-phase continuous-flow magnetophoretic microdevice: Theoretical analysis through computational fluid dynamics simulation. J. Phys. Chem. C 2017, 121, 7466–7477. [Google Scholar] [CrossRef]
- Lim, J.; Yeap, S.P.; Leow, C.H.; Toh, P.Y.; Low, S.C. Magnetophoresis of iron oxide nanoparticles at low field gradient: The role of shape anisotropy. J. Colloid Interface Sci. 2014, 421, 170–177. [Google Scholar] [CrossRef] [PubMed]
- Culbertson, C.T.; Sibbitts, J.; Sellens, K.; Jia, S. Fabrication of Glass Microfluidic Devices. In Microfluidic Electrophoresis: Methods and Protocols; Dutta, D., Ed.; Humana Press: New York, NY, USA, 2019; pp. 1–12. ISBN 978-1-4939-8963-8. [Google Scholar]







| Rectangular Shape (R) | U Shape (U) | |||||
|---|---|---|---|---|---|---|
| L (mm) | 2 | 5 | 10 | 2 | 5 | 10 |
| W (µm) | 300 | 300 | 300 | 280 | 280 | 280 |
| H (µm) | 200 | 200 | 200 | 60 | 60 | 60 |
| Dh (µm) | 240 | 240 | 240 | 97 | 97 | 97 |
| L/Dh | 8 | 21 | 42 | 21 | 51 | 103 |
| Volume (mm3) | 0.12 | 0.3 | 0.6 | 0.03 | 0.08 | 0.15 |
| Rf (1012 Pa·s·m−3) | 0.33 | 0.83 | 1.65 | 6.46 | 16.14 | 32.29 |
| Particle Recovery (%) | Throughput (µL·s−1) | J (-) | Θ (-) | tres (s) | |
|---|---|---|---|---|---|
| U-2 mm | 7.09 | 0.1 | 0.004 | 0.086 | 0.1 |
| U-5 mm | 24.78 | 0.1 | 0.004 | 0.216 | 0.26 |
| U-10 mm | 53.5 | 0.1 | 0.004 | 0.432 | 0.52 |
| R-2 mm | 21.57 | 0.44 | 0.012 | 0.103 | 0.11 |
| R-5 mm | 63.02 | 0.44 | 0.012 | 0.258 | 0.26 |
| R-10 mm | 100 | 0.44 | 0.012 | 0.516 | 0.53 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
González Fernández, C.; Gómez Pastora, J.; Basauri, A.; Fallanza, M.; Bringas, E.; Chalmers, J.J.; Ortiz, I. Continuous-Flow Separation of Magnetic Particles from Biofluids: How Does the Microdevice Geometry Determine the Separation Performance? Sensors 2020, 20, 3030. https://doi.org/10.3390/s20113030
González Fernández C, Gómez Pastora J, Basauri A, Fallanza M, Bringas E, Chalmers JJ, Ortiz I. Continuous-Flow Separation of Magnetic Particles from Biofluids: How Does the Microdevice Geometry Determine the Separation Performance? Sensors. 2020; 20(11):3030. https://doi.org/10.3390/s20113030
Chicago/Turabian StyleGonzález Fernández, Cristina, Jenifer Gómez Pastora, Arantza Basauri, Marcos Fallanza, Eugenio Bringas, Jeffrey J. Chalmers, and Inmaculada Ortiz. 2020. "Continuous-Flow Separation of Magnetic Particles from Biofluids: How Does the Microdevice Geometry Determine the Separation Performance?" Sensors 20, no. 11: 3030. https://doi.org/10.3390/s20113030
APA StyleGonzález Fernández, C., Gómez Pastora, J., Basauri, A., Fallanza, M., Bringas, E., Chalmers, J. J., & Ortiz, I. (2020). Continuous-Flow Separation of Magnetic Particles from Biofluids: How Does the Microdevice Geometry Determine the Separation Performance? Sensors, 20(11), 3030. https://doi.org/10.3390/s20113030