Robust ℋ∞-Fuzzy Logic Control for Enhanced Tracking Performance of a Wheeled Mobile Robot in the Presence of Uncertain Nonlinear Perturbations
Abstract
:1. Introduction
2. Problem Formulation
3. Methodology
3.1. Robust Control Strategy for Treating
3.2. Robust Control Strategy for Treating
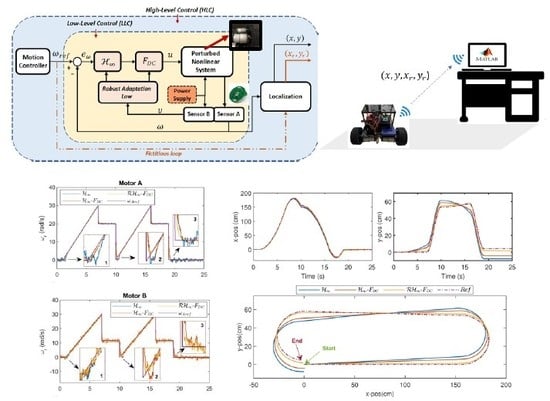
4. Experimental Results
4.1. Speed Tracking
4.2. Path Tracking
4.3. Robust Stability Analysis
5. Discussions and Conclusions
Funding
Acknowledgments
Conflicts of Interest
Notations and Abbreviations
| Notations/ Abbreviations | Descriptions |
| FL, FLC | fuzzy logic, fuzzy logic compensator |
| LMI | linear matrix inequality |
| WMR | wheeled mobile robot |
| LLC | low-level control |
| HLC | high-level-control |
| PWM | pulse-width modulation |
| LFT | linear fractional transformation |
| generalized plant, internally stabilizing controller | |
| compensator designed for Motor A, Motor B | |
| u | control action (input to the perturbed plant) |
| output to the ,FL controller | |
| supply voltage, nominal operating voltage, minimum, maximum supply voltage | |
| deadzone nonlinearity | |
| deadzone bounds (lower, upper, minimum, maximum, best lower, best upper) | |
| perturbed, nominal plant | |
| gain uncertainty of the perturbed plant | |
| midpoint, minimum bound, maximum bound of | |
| , | class of the deadzone, perturbed plant |
| W () | weight that characterizes the spatial structure of the uncertainty (for Motor A, Motor B) |
| actual, desired rotational speed | |
| rotational speed of Motor A, Motor B | |
| rotational speed error of Motor A, Motor B | |
| actual, reference coordinates of the WMR | |
| WMR’s linear, angular velocities | |
| sampling time, final time of execution (in seconds) | |
| , , , | integral of absolute error, instantaneous distance error, total position error, steady-state position error |
| fields of real numbers | |
| fields of positive real numbers | |
| fields of negative real numbers | |
| fields of real matrices |
References
- Yen, S.H.; Tang, P.C.; Lin, Y.C.; Lin, C.Y. A Sensorless and Low-Gain Brushless DC Motor Controller Using a Simplified Dynamic Force Compensator for Robot Arm Application. Sensors 2019, 19, 3171. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alexandridis, A.; Stogiannos, M.; Papaioannou, N.; Zois, E.; Sarimveis, H. An Inverse Neural Controller Based on the Applicability Domain of RBF Network Models. Sensors 2018, 18, 315. [Google Scholar] [CrossRef] [Green Version]
- Shanmugasundram, R.; Zakaraiah, K.; Narri, Y. Effect of parameter variations on the performance of direct current (DC) servomotor drives. J. Vib. Control 2013, 19, 1575–1586. [Google Scholar] [CrossRef]
- Zhang, D.; Lin, L.; Zheng, Q. Error Analysis and Modeling for an Absolute Capacitive Displacement Measuring System with High Accuracy and Long Range. Sensors 2019, 19, 5339. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Yu, F.; Chin, K. Recursive identification of Hammerstein systems with dead-zone nonlinearity in the presence of bounded noise. Int. J. Syst. Sci. 2017, 48, 2394–2404. [Google Scholar] [CrossRef]
- Nemati, A.; Faieghi, M. The Performance Comparison of ANFIS and Hammerstein-Wiener Models for BLDC Motors. In Electronics and Signal Processing; Hu, W., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 29–37. [Google Scholar]
- Peng, J.; Dubay, R. Identification and adaptive neural network control of a DC motor system with dead-zone characteristics. ISA Trans. 2011, 50, 588–598. [Google Scholar] [CrossRef]
- He, W.; Dong, Y.; Sun, C. Adaptive neural network control of unknown nonlinear affine systems with input deadzone and output constraint. ISA Trans. 2015, 58, 96–104. [Google Scholar] [CrossRef]
- Ahmad, N.; Alnaser, M.; Sultan, E.; Alhendi, K. Robust Adaptive Control for a Class of Systems with Deadzone Nonlinearity. Intell. Control Autom. 2015, 6, 10–19. [Google Scholar] [CrossRef] [Green Version]
- Farahani, M.; Bidaki, A.R.Z.; Enshaeieh, M. Intelligent control of a DC motor using a self-constructing wavelet neural network. Syst. Sci. Control Eng. 2014, 2, 261–267. [Google Scholar] [CrossRef]
- Deng, W.; Yao, J. Adaptive integral robust control and application to electromechanical servo systems. ISA Trans. 2017, 67, 256–265. [Google Scholar] [CrossRef]
- El-Nagar, A. Embedded intelligent adaptive PI controller for an electromechanical system. ISA Trans. 2016, 64, 314–327. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.H.; Park, J.H.; Lee, S.W.; Chong, E.K.P. A two-layered fuzzy logic controller for systems with deadzones. IEEE Trans. Ind. Electron. 1994, 41, 155–162. [Google Scholar] [CrossRef]
- Torres Salomao, L.A.; Gámez Cuatzin, H.; Anzurez Marín, J.; Lázaro Castillo, I.I. Fuzzy Logic Control Versus Traditional PI Control Applied to a Fixed Speed Horizontal Axis Wind Turbine. In IAENG Transactions on Engineering Technologies: Special Issue of the World Congress on Engineering and Computer Science 2012; Kim, H.K., Ao, S.I., Amouzegar, M.A., Rieger, B.B., Eds.; Springer: Dordrecht, The Netherlands, 2014; pp. 167–181. [Google Scholar]
- Zhao, Z.Y.; Tomizuka, M.; Isaka, S. Fuzzy gain scheduling of PID controllers. IEEE Trans. Syst. Man Cybern. 1993, 23, 1392–1398. [Google Scholar] [CrossRef] [Green Version]
- Kumar, V.; Mittal, A.P. Parallel fuzzy P+fuzzy I+fuzzy D controller: Design and performance evaluation. Int. J. Autom. Comput. 2010, 7, 463–471. [Google Scholar] [CrossRef]
- Pitalúa-Díaz, N.; Herrera-López, E.J.; Valencia-Palomo, G.; González-Angeles, A.; Rodríguez-Carvajal, R.A.; Cazarez-Castro, N.R. Comparative Analysis between Conventional PI and Fuzzy Logic PI Controllers for Indoor Benzene Concentrations. Sustainability 2015, 7, 5398–5412. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.X.; Hang, C.C.; Liu, C. Parallel structure and tuning of a fuzzy PID controller. Automatica 2000, 36, 673–684. [Google Scholar] [CrossRef]
- Lewis, F.L.; Tim, W.K.; Wang, L.Z.; Li, Z.X. Deadzone compensation in motion control systems using adaptive fuzzy logic control. IEEE Trans. Control Syst. Technol. 1999, 7, 731–742. [Google Scholar] [CrossRef]
- Jang, J.O. A deadzone compensator of a DC motor system using fuzzy logic control. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2001, 31, 42–48. [Google Scholar] [CrossRef]
- Jang, J.O.; Chung, H.T.; Jeon, G.J. Saturation and deadzone compensation of systems using neural network and fuzzy logic. In Proceedings of the 2005 American Control Conference, Portland, OR, USA, 8–10 June 2005; Volume 3, pp. 1715–1720. [Google Scholar]
- Sharma, R.; Gaur, P.; Mittal, A. Design of Two-Layered Fractional Order Fuzzy Logic Controllers Applied to Robotic Manipulator with Variable Payload. Appl. Soft Comput. 2016, 47, 565–576. [Google Scholar] [CrossRef]
- Krjanc, I.; Blazic, S. Predictive Functional Control Based on Fuzzy Model: Design and Stability Study. J. Intell. Robot. Syst. 2005, 43, 283–299. [Google Scholar] [CrossRef]
- Liu, S.; Liu, Y.; Wang, N. Robust adaptive self-organizing neuro-fuzzy tracking control of UUV with system uncertainties and unknown dead-zone nonlinearity. Nonlinear Dyn. 2017, 89, 1397–1414. [Google Scholar] [CrossRef]
- Precup, R.E.; Preitl, S. Development of fuzzy controllers with non-homogeneous dynamics for integral-type plants. Electr. Eng. (Archiv Fur Elektrotechnik) 2003, 85, 155–168. [Google Scholar] [CrossRef]
- Haidegger, T.; Kovács, L.; Preitl, S.; Precup, R.E.; Benyó, B.; Benyó, Z. Controller Design Solutions for Long Distance Telesurgical Applications. Int. J. Artif. Intell. 2011, 6, 48–71. [Google Scholar]
- Yao, J.; Jiao, Z.; Ma, D. Output Feedback Robust Control of Direct Current Motors With Nonlinear Friction Compensation and Disturbance Rejection. J. Dyn. Syst. Meas. Control 2015, 137. [Google Scholar] [CrossRef] [Green Version]
- Zhou, K.; Doyle, J.; Glover, K. Robust and Optimal Control; Prentice Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Park, H.G.; Ahn, K.K.; Park, M.K.; Lee, S.H. Study on Robust Lateral Controller for Differential GPS-Based Autonomous Vehicles. Int. J. Precis. Eng. And Manuf. 2018, 19, 367–376. [Google Scholar] [CrossRef]
- Gillard, J. An overview of linear structural models in errors in variables regression. REVSTAT Stat. J. 2010, 8, 57–80. [Google Scholar]
- Schoukens, J.; Ljung, L. Nonlinear System Identification: A User-Oriented Road Map. IEEE Control Syst. Mag. 2019, 39, 28–99. [Google Scholar]
- Jang, T.; Kim, Y.; Kim, H. Comparison of PID Controllers by Using Linear and Nonlinear Models for Control of Mobile Robot Driving System. J. Korean Soc. Precis. Eng. 2016, 33, 183–190. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, Z. Improvements of direct current motor control and motion trajectory algorithm development for automated guided vehicle. Adv. Mech. Eng. 2019, 11, 1687814018824937. [Google Scholar] [CrossRef] [Green Version]
- Angelina, S.; Afifah, S.; Susamti, P.; Priramadhi, R.; Darlis, D. Efficient energy consumption for indoor mobile robot prototype under illumination. MATEC Web Conf. 2018, 197, 11016. [Google Scholar] [CrossRef]
- Palmieri, N.; Yang, X.S.; De Rango, F.; Marano, S. Comparison of bio-inspired algorithms applied to the coordination of mobile robots considering the energy consumption. Neural Comput. Appl. 2019, 31, 263–286. [Google Scholar] [CrossRef]
- Mei, Y.; Lu, Y.-H.; Hu, Y.C.; Lee, C.S.G. A case study of mobile robot’s energy consumption and conservation techniques. In Proceedings of the 12th International Conference on Advanced Robotics, Seattle, WA, USA, 18–20 July 2005; pp. 492–497. [Google Scholar]
- Tsung, T.T.; Chuang, Y.J.; Chang, H.; Shen, C.L.; Sun, Y.T. Measurement of power and energy consumption of a competition-mobile-robot. MATEC Web Conf. 2017, 119, 01002. [Google Scholar] [CrossRef]
- Hou, L.; Zhang, L.; Kim, J. Energy Modeling and Power Measurement for Mobile Robots. Energies 2019, 12, 27. [Google Scholar] [CrossRef] [Green Version]
- Abukhalil, T.; Al-Mahafzah, H.; Alksasbeh, M.; Alqaralleh, B. Power Optimization in Mobile Robots Using a Real-Time Heuristic. J. Robot. 2020, 2020, 1–8. [Google Scholar] [CrossRef]
















| Type | Frequency | Amplitude | Type | Frequency | Amplitude | ||
|---|---|---|---|---|---|---|---|
| (rad/s) | (PWM) | (rad/s) | (PWM) | ||||
| Step | 0 | 10 | Ramp | 80 | |||
| Step | 20 | Ramp | 50 | ||||
| Step | 5 | Sine | 50 | ||||
| Step | 15 | Sine | 40 | ||||
| Ramp | 0 | 70 | Sine | 60 |
| Hardware | Descriptions |
|---|---|
| Microcontroller unit | ATmega2560; Sampling time = s |
| Motors A and B | Brushed type; Load speed: rad/s; |
| Rated voltage: 12 V; Rated current mA; | |
| Weight g; Motor Driver: TB6612FNG | |
| Hall effect sensors | Quadrature encoding; 390 lines per resolution |
| Voltage sensor | Input voltage range, to 25 V |
| Output voltage range, : 0 to 5 V | |
| (acts as a voltage divider with k, and k) | |
| Wireless Modules | Digi Xbee-S2C 2.4 GHz RF transceiver modules |
| >WMR | Azimuth length between wheels (D): 0.17 m |
| Wheel’s radius (r): 0.07 m; Weight kg | |
| Size () ≈ 0.19 m × 0.17 m × 0.11 m |
| Experiment | Controller | ||
|---|---|---|---|
| - | - | ||
| Exp. 1.1 | 9.5805 | 9.2610 | 6.8687 |
| Exp. 1.2 | 8.4911 | 8.1733 | 6.8213 |
| Exp. 1.3 | 7.5606 | 7.2178 | 4.4691 |
| Average | 8.5441 | 8.2174 | 6.0530 |
| Performance Index | Controller | ||
|---|---|---|---|
| - | - | ||
| for (rad) | 15.08 | 12.38 | 11.50 |
| for (rad) | 15.80 | 15.74 | 13.01 |
| (cm) | 13.16 | 9.053 | 4.162 |
| (cm s) | 207.1 | 138.1 | 52.19 |
| (cm) | 12.33 | 9.002 | 2.729 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, N.S. Robust ℋ∞-Fuzzy Logic Control for Enhanced Tracking Performance of a Wheeled Mobile Robot in the Presence of Uncertain Nonlinear Perturbations. Sensors 2020, 20, 3673. https://doi.org/10.3390/s20133673
Ahmad NS. Robust ℋ∞-Fuzzy Logic Control for Enhanced Tracking Performance of a Wheeled Mobile Robot in the Presence of Uncertain Nonlinear Perturbations. Sensors. 2020; 20(13):3673. https://doi.org/10.3390/s20133673
Chicago/Turabian StyleAhmad, Nur Syazreen. 2020. "Robust ℋ∞-Fuzzy Logic Control for Enhanced Tracking Performance of a Wheeled Mobile Robot in the Presence of Uncertain Nonlinear Perturbations" Sensors 20, no. 13: 3673. https://doi.org/10.3390/s20133673
APA StyleAhmad, N. S. (2020). Robust ℋ∞-Fuzzy Logic Control for Enhanced Tracking Performance of a Wheeled Mobile Robot in the Presence of Uncertain Nonlinear Perturbations. Sensors, 20(13), 3673. https://doi.org/10.3390/s20133673