Theoretical and Experimental Investigations of a Pseudo-Magnetic Levitation System for Energy Harvesting
Abstract
:1. Introduction
1.1. Energy Harvesting
1.2. Pseudo-Magnetic Levitation Harvesters
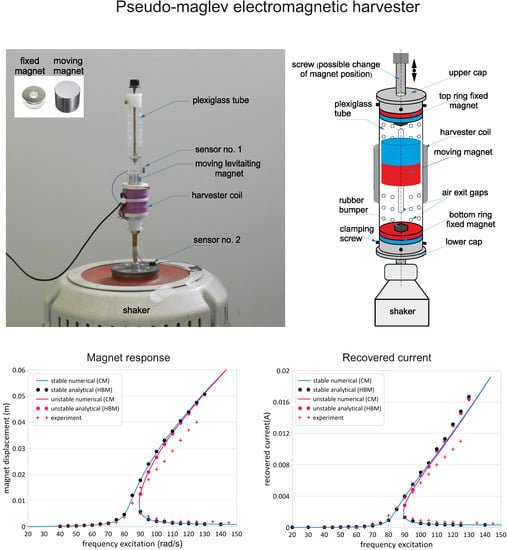
2. Energy Harvesting System Design
2.1. Magnetic Levitation Architectures
2.2. Mathematical Model
2.3. Shaker Test
3. Harmonic Balance Method (HBM)
3.1. Stability Analysis
3.2. Approximate Analytical Solutions
4. Methods
5. Results and Discussion
5.1. Single Pseudo-Levitating Magnet Vibration Centre Shift
5.2. Analytical Results
5.3. Experimental Verification
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| HBM | harmonic balance method |
| EH | energy harvesting |
| maglev | magnetic levitation |
| CM | continuation method |
| emf | electromotive force |
| edf | electrodynamic (Lorentz) force |
References
- European Center for Power Electronics (ECPE). Position Paper on Energy Efficiency—The Role of Power Electronics. March 2007. Available online: https://www.ecpe.org (accessed on 20 January 2020).
- Kilner, J.A.; Skinner, S.J.; Irvine, S.J.C.; Edwards, P.P. (Eds.) Functional Materials for Sustainable Energy Applications; Woodhead Publishing: Cambridge, UK, 2012. [Google Scholar]
- Slabov, V.; Kopyl, S.; Dos Santos, M.P.S.; Kholkin, A.L. Natural and eco-friendly materials for triboelectric energy harvesting. Nano-Micro Lett. 2020, 12, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Tarelho, J.P.G.; Dos Santos, M.P.S.; Ferreira, J.A.F.; Ramos, A.; Kopyl, S.; Kim, S.O.; Hong, S.; Kholkin, A. Graphene-based materials and structures for energy harvesting with fluids—A review. Mater. Today 2018, 21, 1019–1041. [Google Scholar] [CrossRef]
- Spreemann, D.; Manoli, Y. (Eds.) Electromagnetic Vibration Energy Harvesting Devices: Architectures, Designs, Modeling and Optimization, Advanced Microelectronics; Springer: New York, NY, USA, 2012. [Google Scholar]
- Shaikh, F.K.; Zeadally, S. Energy harvesting in wireless sensor networks: A comprehensive review. Renew. Sustain. Energy Rev. 2016, 55, 1041–1054. [Google Scholar] [CrossRef]
- Qing, X.; Li, W.; Wang, Y.; Sun, H. Piezoelectric transducer-based structural health monitoring for aircraft in applications. Sensors 2019, 19, 545. [Google Scholar] [CrossRef] [PubMed]
- Korosak, Z.; Suhadolnik, N.; Pletersek, A. The implementation of a low power environmental monitoring and soil moisture measurement system based on UHF RFID. Sensors 2019, 19, 5527. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bernardo, R.; Rodrigues, A.; Dos Santos, M.P.S.; Carneiro, P.; Lopes, A.; Amaral, J.S.; Amaral, V.S.; Morais, R. Novel magnetic stimulation methodology for low-current implantable medical devices. Med. Eng. Phys. 2019, 73, 77–84. [Google Scholar] [CrossRef] [PubMed]
- Dos Santos, M.P.; Ferreira, J.A.F.; Simões, J.A.O.; Pascoal, R.; Torrao, J.; Xue, X.; Furlani, E.P. Magnetic levitation-based electromagnetic energy harvesting: A semi-analytical non-linear model for energy transduction. Sci. Rep. 2016, 6, 18579. [Google Scholar] [CrossRef]
- Kaleta, J.; Mech, R.; Wiewiorski, P. Energy harvester based on magnetomechanical effect as a power source for multi-node wireless network. Small-scale energy harvesting. In A Guide to Small-Scale Energy Harvesting Techniques; Lallart, M., Ed.; IntechOpen: London, UK, 2012. [Google Scholar]
- Liu, X.; Zhang, X.; Jia, M.; Fan, L.; Lu, W.; Zhai, Z. 5G-based green broadband communication system design with simultaneous wireless information and power transfer. Phys. Commun. 2018, 28, 130–137. [Google Scholar] [CrossRef]
- Liu, X.; Li, F.; Na, Z. Optimal resource allocation in simultaneous cooperative spectrum sensing and energy harvesting for multichannel cognitive radio. IEEE Access 2017, 5, 3801–3812. [Google Scholar] [CrossRef]
- Cepnik, C.; Lausecker, R.; Wallrabe, U. Review on electrodynamic energy harvestersa classification approach. Micromachines 2013, 5, 168–196. [Google Scholar] [CrossRef] [Green Version]
- Williams, C.B.; Yates, R.B. Analysis of a micro-electric generator for microsystems. Sens. Actuators A Phys. 1996, 52, 8–11. [Google Scholar] [CrossRef]
- Mitcheson, P.D.; Green, T.C.; Yeatman, E.M.; Holmes, A.S. Architectures for vibration-driven micropower generators. J. Miecroelectromech. Syst. 2004, 13, 429–440. [Google Scholar] [CrossRef] [Green Version]
- Stephen, N.G. On energy harvesting from ambient vibration. J. Sound Vib. 2006, 293, 409–425. [Google Scholar] [CrossRef] [Green Version]
- Beeby, S.P.; Tudor, M.J.; White, N.M. Energy harvesting vibration sources for microsystems applications. Meas. Sci. Technol. 2006, 17, R175. [Google Scholar] [CrossRef]
- Jiang, W.A.; Chen, L.Q. Energy harvesting of monostable Duffing oscillator under Gaussian white noise excitation. Mech. Res. Commun. 2013, 53, 85–91. [Google Scholar] [CrossRef]
- Zhou, S.; Cao, J.; Inman, D.J.; Lin, J.; Liu, S.; Wang, Z. Broadband tri-stable energy harvester: Modelling and experiment verification. Appl. Energy 2014, 133, 33–39. [Google Scholar] [CrossRef]
- Jiang, W.A.; Chen, L.Q. A piezoelectric energy harvester based on internal resonance. Acta Mech. Sin. 2015, 31, 223–228. [Google Scholar]
- Sun, K.; Liu, G.Q.; Xu, X.Y. A piezoelectric energy harvester based on internal resonance. Appl. Mech. Mater. 2011, 128–129, 923–927. [Google Scholar] [CrossRef]
- Saha, C.; O’Donnell, T.; Wang, N.; McCloskey, P. Electromagnetic generator for harvesting energy from human motion. Sens. Actuators A Phys. 2008, 147, 248–253. [Google Scholar] [CrossRef]
- Dallago, E.; Marchesi, M.; Venchi, G. Analytical model of a vibrating electromagnetic harvester considering nonlinear effects. IEEE Trans. Power Electron. 2010, 25, 1989–1997. [Google Scholar] [CrossRef]
- Bernal, A.; Garcia, L. The modelling of an electromagnetic energy harvesting architecture. Appl. Math. Model. 2012, 36, 4728–4741. [Google Scholar] [CrossRef]
- Mann, B.; Sims, N. Energy harvesting from the nonlinear oscillations of magnetic levitation. J. Sound Vib. 2009, 319, 515–530. [Google Scholar] [CrossRef] [Green Version]
- Mann, B.; Sims, N. On the performance and resonant frequency of electromagnetic induction energy harvesters. J. Sound Vib. 2010, 329, 1348–1361. [Google Scholar] [CrossRef] [Green Version]
- Dos Santos, M.P.S.; Coutinho, J.; Marote, A.; Sousa, B.; Ramos, A.; Ferreira, J.A.F.; Bernardo, R.; Rodrigues, A.; Marques, A.T.; Da Cruz e Silva, O.A.B.; et al. Capacitive technologies for highly controlled and personalized electrical stimulation by implantable biomedical systems. Sci. Rep. 2019, 9, 5001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berdy, D.F.; Valentino, D.J.; Peroulis, D. Kinetic energy harvesting from human walking and running using a magnetic levitation energy harvester. Sens. Actuators A Phys. 2015, 222, 262–271. [Google Scholar] [CrossRef]
- Carneiro, P.; Dos Santos, M.P.S.; Rodrigues, A.; Ferreira, J.A.F.; Simoes, J.A.O.; Marques, A.T.; Kholkin, A.L. Electromagnetic energy harvesting using magnetic levitation architectures: A review. Sens. Actuators A Phys. 2020, 260, 114191. [Google Scholar] [CrossRef]
- Kecik, K. Assessment of energy harvesting and vibration mitigation of a pendulum dynamic absorber. Mech. Syst. Signal Process. 2018, 106, 198–209. [Google Scholar] [CrossRef]
- Kecik, K.; Mitura, A.; Lenci, S.; Warminski, J. Energy harvesting from a magnetic levitation system. Int. J. Nonliner Mech. 2017, 94, 200–206. [Google Scholar] [CrossRef]
- Gieras, J.; Kucharski, A.; Piechowski, J. Performance characteristics of a shake flashlight. In Proceedings of the 2017 IEEE International Electric Machines and Drives Conference (IEMDC), Miami, FL, USA, 21–24 May 2017. [Google Scholar]
- Kecik, K. Architecture and optimization of a low-frequency maglev energy harvester. Int. J. Struct. Stab. Dyn. 2019, 8, 1–13. [Google Scholar] [CrossRef]
- Munaz, A.; Lee, B.; Chung, G. A study of an electromagnetic energy harvester using multi-pole magnet. Sens. Actuators A Phys. 2013, 201, 134–140. [Google Scholar] [CrossRef]
- Yurchenko, D.; Alevras, P. Parametric pendulum based wave energy converter. Mech. Syst. Signal Process 2018, 99, 504–515. [Google Scholar] [CrossRef] [Green Version]
- Doedel, E.; Oldeman, B. Auto-07p: Continuation and Bifurcation Software; Concordia Univ. Canada: Montreal, QC, Canada, 2012; Available online: http://indy.cs.concordia.ca/auto/ (accessed on 20 January 2020).
- Medina, N.; Vicente, J.; Robles, J. Magnetic fields influence on sensors with electrical output under sinusoidal excitations. Acta IMEKO 2016, 5, 51–58. [Google Scholar] [CrossRef] [Green Version]














© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kecik, K.; Mitura, A. Theoretical and Experimental Investigations of a Pseudo-Magnetic Levitation System for Energy Harvesting. Sensors 2020, 20, 1623. https://doi.org/10.3390/s20061623
Kecik K, Mitura A. Theoretical and Experimental Investigations of a Pseudo-Magnetic Levitation System for Energy Harvesting. Sensors. 2020; 20(6):1623. https://doi.org/10.3390/s20061623
Chicago/Turabian StyleKecik, Krzysztof, and Andrzej Mitura. 2020. "Theoretical and Experimental Investigations of a Pseudo-Magnetic Levitation System for Energy Harvesting" Sensors 20, no. 6: 1623. https://doi.org/10.3390/s20061623
APA StyleKecik, K., & Mitura, A. (2020). Theoretical and Experimental Investigations of a Pseudo-Magnetic Levitation System for Energy Harvesting. Sensors, 20(6), 1623. https://doi.org/10.3390/s20061623