Straight Long-Range Surface Plasmon Polariton Waveguide Sensor Operating at λ0 = 850 nm
Abstract
:1. Introduction
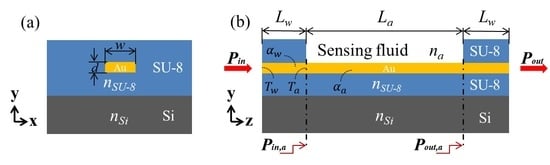
2. Sensor Structure
3. Design and Optimization
3.1. Single-Mode LRSPP Waveguide
3.2. Attenuation
3.3. Coupling Loss
3.4. Sensing Length
4. Results and Discussion
5. Experiment
5.1. Sensor Fabrication
5.2. Characterization
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fan, H.; Buckley, R.; Berini, P. Passive long-range surface plasmon-polariton devices in Cytop. Appl. Opt. 2012, 51, 1459–1467. [Google Scholar] [CrossRef]
- Berini, P. Bulk and surface sensitivities of surface plasmon waveguides. New J. Phys. 2008, 10, 105010. [Google Scholar] [CrossRef]
- Breukelaar, I.; Charbonneau, R.; Berini, P. Long-range surface plasmon-polariton mode cutoff and radiation in embedded strip waveguides. J. Appl. Phys. 2006, 100, 043104. [Google Scholar] [CrossRef]
- Wong, W.; Adikan, F.; Berini, P. Long-range surface plasmon Y-junctions for referenced biosensing. Opt. Express 2015, 23, 31098. [Google Scholar] [CrossRef] [PubMed]
- Fan, H.; Berini, P. Bulk sensing using a long-range surface-plasmon triple-output Mach-Zehnder interferometer. IEEE J. Lightwave Technol. 2018, 34, 2631–2638. [Google Scholar] [CrossRef]
- Khan, A.; Krupin, O.; Lisicka-Skrzek, E.; Berini, P. Mach-Zehnder refractometric sensor using long-range surface plasmon waveguides. Appl. Phys. Lett. 2013, 103, 111108. [Google Scholar] [CrossRef]
- Wong, W.; Berini, P.; Fan, H.; Adikan, F.R.M. Multichannel long-range surface plasmon waveguides for parallel biosensing. IEEE J. Lightwave Technol. 2018, 36, 5536–5546. [Google Scholar] [CrossRef]
- Oleksiy, K.; Hamoudi, A.; Chen, W.; Tait, R.N.; Berini, P. Biosensing using straight long-range surface plasmon waveguides. Opt. Express 2013, 21, 698–709. [Google Scholar]
- Schmidt, S.; Flueckiger, J.; Wu, W.; Grist, S.M.; Fard, S.T.; Donzella, V.; Khumwan, P.; Thompson, E.R.; Wang, Q.; Kulik, P.; et al. Improving the performance of silicon photonic rings, disks, and bragg gratings for use in label-free biosensing. SPIE 2014, 9166, 1–38. [Google Scholar]
- Salleh, M.; Glidle, A.; Sorel, M.; Reboud, J.; Cooper, J. Polymer dual ring resonators for label-free optical biosensing using microfluidics. Chem. Commun. 2013, 49, 3095–3097. [Google Scholar] [CrossRef] [Green Version]
- Halldorsson, J.; Arnfinnsdottir, N.; Jonsdottir, A.; Agnarsson, B.; Leosson, K. High index contrast polymer waveguide platform for integrated biophotonics. Opt. Express 2010, 18, 16217–16226. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Sun, J.; Liu, Y.; Sun, J.-W.; Chen, C.-M.; Sun, X.-Q.; Wang, F.; Zhang, D.-M. 650-nm 1 × 2 polymeric thermo-optic switch with low power consumption. Opt. Express 2014, 22, 11119–11128. [Google Scholar] [CrossRef] [PubMed]
- Kou, L.; Labrie, D.; Chylek, P. Refractive indices of water and ice in the 0.65-to 2.5-µm spectral range. Appl. Opt. 1993, 32, 3531–3540. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Slavik, R.; Homola, J. Ultrahigh resolution long range surface plasmon-based sensor. Sens. Actuators B Chem. 2008, B123, 10–12. [Google Scholar] [CrossRef]
- Joo, Y.; Song, S.; Magnusson, R. Demonstration of long-range surface plasmon-polariton waveguide sensors with asymmetric double electrode structures. Appl. Phys. Lett. 2010, 97, 201105. [Google Scholar] [CrossRef]
- Wark, A.; Lee, H.; Corn, R. Long-range surface plasmon resonance imaging for bioaffinity sensors. Anal. Chem. 2005, 77, 3904–3907. [Google Scholar] [CrossRef]
- Ji, L.; Sun, X.; He, G.; Liu, Y.; Wang, X.; Yi, Y.; Chen, C.; Wang, F.; Zhang, D. Surface plasmon resonance refractive index sensor based on ultraviolet bleached polymer waveguide. Sens. Actuators B Chem. 2017, 244, 373–379. [Google Scholar] [CrossRef]
- Ji, L.; Sun, X.; Yang, G.; Sun, X.; Yi, Y.; Wang, X.; Chen, C.; Zhang, D. SU-8 grating assisted intermodal interference in surface plasmon polariton waveguide. Opt. Mater. Express 2017, 7, 2560–2570. [Google Scholar] [CrossRef]
- Huang, S.; Lai, C.; Sheu, F.; Tsai, W.-S. Characterization of long-range plasmonic waveguides at visible to near-infrared regime. AIP Adv. 2017, 7, 125221. [Google Scholar] [CrossRef]
- Prajzler, V.; Nekvindova, P.; Hyps, P.; Lyutakov, O.; Jeřábek, V. Flexible polymer planar optical waveguides. Radio Eng. 2014, 23, 776–782. [Google Scholar]
- Yakubovsky, D.; Arsenin, A.; Stebunov, Y.; Fedyanin, D.Y.; Volkov, V.S. Optical constants and structural properties of thin gold films. Opt. Express 2017, 25, 25574–25587. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berini, P. Long-range surface plasmon-polariton waveguides in silica. J. Appl. Phys. 2007, 102, 053105. [Google Scholar] [CrossRef]
- Liu, W.; Yan, J.; Shi, Y. High sensitivity visible light refractive index sensor based on high order mode Si3N4 photonic crystal nanobeam cavity. Opt. Express 2017, 25, 31739. [Google Scholar] [CrossRef] [PubMed]
- Cai, H.; Yang, Y.; Chen, X.; AliMohammad, M.; Ye, T.-X.; Guo, C.-R.; Yi, L.-T.; Zhou, C.-J.; Liu, J.; Ren, T.-L. A third-order mode high frequency biosensor with atomic resolution. Biosens. Bioelectron. 2015, 71, 261–268. [Google Scholar] [CrossRef]
- Jhonattan, C.; Gabrielli, L.H.; Lechuga, L.M.; Figueroa, H.E.H. Trimodal waveguide demonstration and its implementation as a high order mode interferometer for sensing application. Sensors 2019, 19, 2821. [Google Scholar]
- Charbonneau, R.; Scales, C.; Breukelaar, I.; Fafard, S.; Lahoud, N.; Mattiussi, G.; Berini, P. Passive integrated optics elements based on long-range surface plasmon polaritons. IEEE J. Lightwave Technol. 2006, 24, 477–494. [Google Scholar] [CrossRef]
- Wong, W.; Krupin, O.; Mahamd, A.; Berini, P. Optimization of long-range surface plasmon waveguides for attenuation-based biosensing. IEEE J. Lightwave Technol. 2015, 33, 3234–3242. [Google Scholar] [CrossRef]
- Wong, W.; Mahamd, A.; Berini, P. Surface sensitivity of straight long-range surface plasmon waveguides for attenuation-based biosensing. Appl. Phys. A 2014, 117, 527–535. [Google Scholar] [CrossRef]
- Tai, Y.; Wei, P. Sensitive liquid refractive index sensors using tapered optical fiber tips. Opt. Lett. 2010, 35, 944–946. [Google Scholar] [CrossRef]
- Mallik, A. High sensitivity refractive index sensor based on a tapered small core single-mode fiber structure. Opt. Lett. 2015, 40, 4166–4169. [Google Scholar]
- Feng, D.; Liu, G.; Liu, X.; Jiang, M.-S.; Sui, Q.-M. Refractive index sensor based on plastic optical fiber with tapered structure. Appl. Opt. 2014, 53, 2007–2011. [Google Scholar]
- Madaan, D.; Kapoor, A.; Sharma, V. Ultrahigh sensitivity plasmonic refractive-index sensor for aqueous environment. IEEE Photon. Technol. Lett. 2018, 30, 149–152. [Google Scholar] [CrossRef]
- Sun, X.; Dai, D.; Thylén, L.; Wosinski, L. High-sensitivity liquid refractive-index sensor based on a Mach-Zehnder interferometer with a double-slot hybrid plasmonic waveguide. Opt. Express 2015, 23, 25688–25699. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Liu, B.; Zhu, X.; Tang, X.-L.; Shi, Y.-W. Long-range surface plasmon resonance sensor based on dielectric/silver coated hollow fiber with enhanced figure of merit. Opt. Lett. 2015, 40, 744–747. [Google Scholar] [CrossRef]
- Vernoux, C.; Chen, Y.; Markey, L.; Spârchez, C.; Arocas, J.; Felder, T.; Neitz, M.; Brusberg, L.; Weeber, J.; Bozhevolnyi, S.I.; et al. Flexible long-range surface plasmon polariton single-mode waveguide for optical interconnects. Opt. Mater. Express 2018, 8, 469–484. [Google Scholar] [CrossRef]
- Tang, J.; Liu, Y.; Zhang, L.; Fu, X.-C.; Xue, X.-M.; Qian, G.; Zhao, N.; Zhang, T. Flexible thermo-optic variable attenuator based on long-range surface plasmon-polariton waveguides. Micromachines 2018, 9, 369. [Google Scholar] [CrossRef] [Green Version]













| na | Power in Au (%) | Power in SU-8 (%) | Power in Analyte (%) | MPA (dB/mm) | Sensitivity (dB/RIU/mm) |
|---|---|---|---|---|---|
| 1.562 | 0.048 | 58.795 | 41.181 | 14.36 | 196 |
| 1.566 | 0.044 | 55.089 | 44.862 | 13.00 | |
| 1.570 | 0.042 | 52.331 | 47.597 | 12.21 | |
| 1.574 | 0.041 | 49.992 | 49.992 | 12.01 | |
| 1.578 | 0.042 | 47.637 | 52.290 | 12.35 | 188 |
| 1.582 | 0.045 | 45.058 | 54.917 | 13.15 | |
| 1.586 | 0.048 | 41.737 | 58.221 | 14.25 |
| Platform | Structure | RI Range | Sensitivity | Wavelength | Size | Ref |
|---|---|---|---|---|---|---|
| Fiber | Tapered core | 1.3–1.4 | 8000%/RIU | 632 nm | NA | [29] |
| Fiber | Tapered core | 1.4304–1.4320 | 19,212.5 nm/RIU | 1474–1615 nm | NA | [30] |
| POF | Tapered core | 1.33–1.41 | 950 μW/RIU @633 nm | 532, 633, and 780 nm | NA | [31] |
| Hybrid-plasmonic | Straight waveguide | 1.3306–1.3326 | 2 × 105 dB/RIU | 632.8 nm | 75 μm | [32] |
| Hybrid-plasmonic | Dual slot waveguide | 10–100% IPA | 1061 nm/RIU | 1550 nm | 40 μm | [33] |
| LRSPR | Prism | 1.518–1.576 | 2000–6600 nm/RIU | 400–800 nm | NA | [34] |
| This work | Straight waveguide | 1.562–1.586 | 196 dB/RIU/mm | 850 nm | <3 mm |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Wang, F.; Gao, Y.; Zhang, D.; Sun, X.; Berini, P. Straight Long-Range Surface Plasmon Polariton Waveguide Sensor Operating at λ0 = 850 nm. Sensors 2020, 20, 2507. https://doi.org/10.3390/s20092507
Xu Y, Wang F, Gao Y, Zhang D, Sun X, Berini P. Straight Long-Range Surface Plasmon Polariton Waveguide Sensor Operating at λ0 = 850 nm. Sensors. 2020; 20(9):2507. https://doi.org/10.3390/s20092507
Chicago/Turabian StyleXu, Yan, Fei Wang, Yang Gao, Daming Zhang, Xiaoqiang Sun, and Pierre Berini. 2020. "Straight Long-Range Surface Plasmon Polariton Waveguide Sensor Operating at λ0 = 850 nm" Sensors 20, no. 9: 2507. https://doi.org/10.3390/s20092507
APA StyleXu, Y., Wang, F., Gao, Y., Zhang, D., Sun, X., & Berini, P. (2020). Straight Long-Range Surface Plasmon Polariton Waveguide Sensor Operating at λ0 = 850 nm. Sensors, 20(9), 2507. https://doi.org/10.3390/s20092507