1. Introduction
Edge computing refers to the deployment of computation closer to data sources (edge) [
1], rather than more centrally as is the case with cloud computing. It can address latency, privacy and scalability issues faced by cloud-based systems [
2,
3]. In terms of latency, moving computation closer to the data sources decreases end-to-end network latency. In terms of privacy, computation performed at the edge or at a local trusted edge server prevents data from leaving the device, potentially reducing the chance for cyber-attacks. In terms of scalability, edge computing can avoid network bottlenecks at central servers by enabling a hierarchical architecture of edge nodes [
4]. Moreover, edge computing can address energy-aware and bandwidth saving applications [
5].
For data processing and information inference, it is also possible to embed intelligence at edge devices, which can be enabled by machine learning (ML) algorithms [
6,
7]. Deep learning [
8], a subset of Machine Learning, can be implemented on edge devices, such as mobile phones, wearables and the Internet of Things (IoT) nodes [
9,
10]. Deep learning is more resilient to noise and able to deal with non-linearity. Instead of relying on hand-crafted features, deep learning automatically extracts the best possible features during its training phase. During training, the deep neural network architecture can extract very coarse low-level features in its first layer, recognise finer and higher-level features in its intermediate layers and achieve the targeted values in the final layer [
11].
Efficient deep learning design (e.g., deep neural networks) for embedded devices can be achieved by optimising both algorithmic (software) and hardware aspects [
11]. At the algorithmic level, two methods can be implemented, namely model design and model compression [
4]. In model design, researchers focus on designing deep learning models with a reduced number of parameters. This results in reduced memory size and latency, while trying to maintain high accuracy. In model compression, models are adapted for edge deployment by applying a number of different techniques on a trained model, such as parameter quantisation, parameter pruning and knowledge distillation. Parameter quantisation is a conversion technique to reduce model size with minimal degradation in model accuracy. Parameter pruning eliminates the least essential values in weight tensors. This method is related to the dropout technique [
12]. Knowledge distillation [
13] creates a smaller deep learning model by mimicking the behaviour of a larger model. It can be realised by training the smaller model using the outputs obtained from the larger model. At the hardware level, the training and inferencing processes of deep learning models can be accelerated by the computation power of server-class central processing units (CPUs), graphics processing unit (GPUs), tensor processing units (TPUs), neural processing units (NPUs), application-specific circuits (ASICs) and field-programmable gate arrays (FPGAs). Deep learning accelerators with diversity of layers and kernels built from custom low density FPGAs can provide high-speed computation while maintaining reconfigurability [
14]. Both ASICs and FPGAs are generally more energy-efficient than conventional CPUs and GPUs [
4].
Deep learning at the edge can be applied for air pollution prediction. Air pollution exposure causes negative impacts on human health [
15,
16] and economic activities [
17]. Among many air pollutants, particulate matter (PM) harms the human respiratory system, as it may enter into the human respiratory tract or even the lungs through inhalation [
18,
19]. Particulate matter can be in the form of PM
2.5 (particulate matter with diameter less than 2.5 μm, or fine particles) and PM
10 (diameter less than 10 μm, or inhalable particles) [
20]. It may lead to lung cancer [
20], affect cardiovascular diseases [
21] and even result in death [
22]. Particulate matter causes premature death, and it is considered as responsible for 16% of global deaths [
23]. The complex mixture of particulate matter and other gases like ozone was recorded to be associated with an all-cause death rate of up to 9 million in 2015 [
24]. In this connection, building a forecasting system based on hourly air quality prediction plays an important role in health alerts [
25].
Many works on PM2.5 prediction considered only the performance evaluation by comparing predicted values to the dataset for accuracy. Our work aims to extend this body of work around deep learning models for air quality monitoring by analysing the deployment of these models to edge devices. In this work, our main contributions are:
- (1)
designing a novel hybrid deep learning model for PM2.5 pollutant level prediction based on an available dataset;
- (2)
optimising the obtained model to a lightweight version suitable for edge devices; and
- (3)
examining model performance when running on the edge devices.
We implement post-training quantisation as a part of the algorithmic-level optimisation. This technique compresses model parameters by converting floating-point numbers to reduced precision numbers. Quantisation can improve CPU and hardware accelerator latencies and potentially reduce the original deep learning model size.
The remainder of this paper is structured as follows.
Section 2 summarises the related work and clarifies our originality.
Section 3 explains some of the basic theories related to this research.
Section 4 describes the dataset and the required preprocessing, as well as defining our proposed deep learning model and gives a brief overview of the edge devices used in this work.
Section 5 presents the results of our proposed model in terms of prediction accuracy and explains the model optimisation results for the selected edge devices.
Section 6 offers conclusions and discusses future work.
2. Related Work
Various work been published in the last few years around the use of deep learning for air quality prediction. Navares and Aznarte [
26] implemented Long Short-Term Memory (LSTM) to predict PM
10 and other air pollutants. They demonstrated a Recurrent Neural Network (RNN) that can map input sequences to output sequences by including the past context into its internal state, making it suitable for time-series problems. However, as the time series grows, relevant information occurs further in the past making RNNs unable to connect suitable information. Moreover, RNNs suffer from the vanishing gradient problem due to cyclic loops.
LSTMs, a variation of RNNs, are capable of learning long-term dependencies and are able to deal with vanishing gradients. Li et al. [
27] predicted hourly PM
2.5 concentration by using an LSTM model. The authors combined historical air pollutant data, meteorological data, and time stamp data. For one-hour predictions, the proposed LSTM model outperformed other models such as the spatiotemporal deep learning (STDL), time-delay neural network (TDNN), autoregressive moving average (ARMA) and support vector regression (SVR) models. Xayasouk et al. [
28] implemented LSTM and Deep Autoencoder to predict 10-day of PM
2.5 and PM
10 concentrations. By varying the input batch size and recording the total average of the model performances, the proposed LSTM model was more accurate than the DAE model. Seng et al. [
29] used LSTM model to predict air pollutant data (PM
2.5, CO, NO
2, O
3, SO
2) at 35 monitoring stations in Beijing. They proposed a comprehensive model called multi-output and multi-index of supervised learning (MMSL) based on spatiotemporal data of present and surrounding stations. The effectiveness of the proposed model was compared to the existing time series model (Linear Regression, SVR, Random Forest and ARMA) and baseline models (CNN-LSTM and CNN-Bidirectional RNN). Xu et al. [
30] proposed a framework called HighAir. This framework used hierarchical graph neural network based on encoder-decoder architecture. Both encoder and decoder consist of LSTM network. Other works based on LSTMs are also reported in [
31,
32].
Other researchers have also proposed hybrid deep learning models. Zhao et al. [
33] compared ANN, LSTM and LSTM-Fully Connected (LSTM-FC) models to predict PM
2.5 concentrations. They found that LSTM-FC produced better predictive performance. Their model consists of two parts. In the first, the LSTM was applied to model the local PM
2.5 concentrations. In the second, the fully connected network was used to capture the spatial dependencies between the central station and neighbour stations. The combination of CNN and LSTM models have also been actively explored [
18,
34,
35,
36]. CNN-LSTM may improve the accuracy for PM
2.5 prediction, as reported by Li et al. [
37], where the authors implemented a 1D CNN to extract features from sequence data and used LSTM to predict future values. In many real problems, input data may come from many resources, constructing spatiotemporal dependencies as explained by Qi et al. [
34]. Gated Recurrent Units (GRUs), another variant of RNNs, have also been applied to PM
2.5 prediction. Tao et al. [
38] combined a one-dimensional CNN with bi-directional GRU to forecast PM
2.5 concentration. They examined attributes in the dataset to find the best input features for the proposed model and evaluated the model performance based on mean absolute error (MAE), root mean square error (RMSE) and symmetric mean absolute percentage error (SMAPE). Powered by AI cloud computing to interpret multimode data, a new framework based on CNN-RNN was proposed by Chen et al. [
39] to predict PM
2.5 values. The framework consists of input preprocessing stages, CNN encoder, RNN-based learning network and CNN Decoder. The input model considered the spatiotemporal factor in the form of 4D sequence data of heat maps.
Various deep learning optimisation techniques have been proposed recently. Even though the selected case studies in these works might not be related to air quality prediction, we review some of them as follows. Post-trained model size can be reduced by quantising weights and activation function, without retraining the model. This method is called the
post-training quantisation [
40]. Banner et al. [
40] proposed 4-bit post-training quantisation for CNNs. They designed an efficient quantisation method by minimising mean-squared quantization error at the tensor level and avoiding retraining the model. Moreover, a mathematical background review for integer quantisation and its implementation on many existing pre-trained neural network models was presented by Wu et al. [
41]. With 8-bit integer quantisation, the obtained accuracy either matches or is within 1% of the floating-point model. Intended for mobile edge devices, Peng et al. [
42] proposed a fully-integer based quantisation method tested on an ARMv8 CPU. The proposed method achieved comparable accuracy to other state-of-the-art methods. Li and Alvarez [
43] specifically proposed the integer-only quantisation method for LSTM neural network. The obtained result is accurate, efficient and fast to execute. Moreover, the proposed method has been deployed to a variety of target hardware.
To the best of our knowledge, previous work on air quality prediction has not specifically explored optimisation of models for resource-constrained edge devices. Our work aims to extend this body of work around deep learning models for air quality monitoring by analysing the deployment of these models to edge device. We implement post-training quantisation techniques to the baseline model using tools provided by TensorFlow framework [
44] and evaluate the optimised model performance on Raspberry Pi boards.
Table 1 summarises the aforementioned research related to air quality prediction, alongside our contribution.
4. Materials and Methods
4.1. Dataset and Preprocessing
In this study, we use a dataset provided by Zhang et al. [
47], which can be downloaded from the University of California, Irvine (UCI) Machine Learning Repository page. The dataset captures Beijing air quality, collected from 12 different Guokong (state controlled) monitoring sites in Beijing and its surroundings [
47]. These 12 monitoring sites are Aotizhongxin, Changping, Dingling, Dongsi, Guanyuan, Gucheng, Huairou, Nongzhanguan, Shunyi, Tiantan, Wanliu and Wanshouxigong.
Regardless of the real geographical location and the ability for each monitoring site to gather both pollutant and meteorological data, we consider every monitoring site merely as a node. Therefore, we model a complex monitoring site as a simple node. The term node is closely associated with the end device, where the edge computing is usually executed. We are interested only in the data obtained by each node and its correlation with other nodes. We number the 12 monitoring sites as mentioned above, from Aotizhongxin as Node 1, Changping as Node 2, Dingling as Node 3, Dongsi as Node 4, etc.
There are 12 columns (features) and 36,064 rows in the dataset, collected from 1 March 2013 to 28 February 2017. Each row in the dataset is hourly data, composed of pollutant data (PM
2.5, PM
10, SO
2, CO, NO
2, and O
3) and meteorological data (temperature, air pressure, dew point, rain, wind direction and wind speed). We split data into training data and test data. Data from 1 March 2013 to 20 March 2016 are used as training data, whereas data from 21 March 2016 to 28 February 2017 are used as test data. By using this division, there are a total of 26,784 training data and 8280 test data. In this work, we focus on predicting the PM
2.5 concentrations. We evaluated the best model for a short-term prediction, that is 1-h particulate matter concentrations.
Figure 4 shows the PM
2.5 concentrations obtained from Node 1 (Aotizhongxin monitoring site).
Data can be numerical or categorical. The attribute of wind direction in the dataset, which is categorical data, admits 16 values: N, NNE, NE, ENE, E, ESE, SE, SSE, S, SSW, SW, WSW, W, WNW, NW and NNW. These features are label encoded. Dividing 360 degrees by 16 (number of wind directions) and applying floor rounding, we found a label for N is 360, NNE is 22, NE is 45, ENE is 67, etc. Instead of labelling N as 0, we assign it as 360. For missing values in the dataset, we filled them with the last timestamp data.
Besides labelling the categorical data and filling in missing values, we scaled the input features during the training and testing phases. Feature scaling is a method used to normalise the range of independent variables or features of data. In data processing, it is also known as data normalisation and is generally performed during the data preprocessing step. In this work, all inputs are normalised to the range of 0 and 1 (min-max scaler). The general formula for a min-max of [0, 1] is given as:
4.2. Feature Selection
Our work aims to predict PM
2.5. As shown in
Table 2, PM
2.5 are strongly correlated to PM
2.5, NO
2 and CO (with
); moderately correlated to SO
2 (with
); and weakly correlated to O
3 (with
). It is also found that rain (RAIN), air pressure (PRES) and temperature (TEMP) have the weakest correlation with PM
2.5. To obtain the optimum number of input features, only RAIN, PRES and TEMP are varied. Thus, four different combinations are obtained and the values of RMSE and MAE for each combination are recorded, as shown in
Table 3.
Table 3 reports the feature selection process only for Node 1. The results obtained from this step can be applied to all other nodes.
As shown in
Table 3, removing rain during training (11 attributes) yielded the best performance. Thus, PM
2.5, PM
10, SO
2, CO, NO
2, O
3, temperature, air pressure, dew point, wind direction and wind speed were selected as the input features for our model. We use the same input features for all monitoring sites.
To obtain the RMSE and MAE values shown in
Table 3, we used a simple LSTM network as a baseline model before implementing our proposed hybrid model (see
Section 4.3). A one-layer LSTM with 15 neurons was selected as a model predictor. The lookback length of the input is determined by calculating the autocorrelation coefficient among the lagged time series of PM
2.5 data. We set 0.7 as a minimum requirement for high temporal correlation among the lagged data. As shown in
Figure 5, eight samples (including time lag = 0) are selected as the length of the input model. At this time lag, all autocorrelation coefficients have values higher than 0.7 for all monitoring sites. Thus, we used the current sample (time lag = 0) and the previous seven samples to predict one sample in the future.
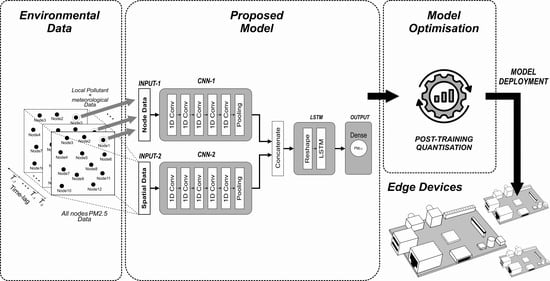
4.3. Proposed Model
In
Section 4.2, we implemented a simple, single-layer LSTM model composed of 15 neurons to evaluate model performance based on different input attributes. From this experiment, we can determine which attributes should be fed to the model. In this section, we propose a hybrid model by combining one-dimensional convolutional neural networks (1D CNN) as feature extractors and feeding the output of these CNNs to an LSTM network, as shown in
Figure 6.
The proposed model is composed of two inputs, both are formed in a parallel structure. In the first input (INPUT-1), only local (present) node data are collected, whereas, in the second input (INPUT-2), all PM
2.5 data obtained from local and surrounding nodes are fed. Local node refers to the node where PM
2.5 is being predicted. Data for INPUT-1 are PM
2.5, PM
10, SO
2, CO, NO
2, O
3, temperature, air pressure, dew point, wind direction and wind speed (11 features in total). Eight timesteps (lookback) of these inputs are used to predict one hour of PM
2.5 in the future. Each batch of inputs is fed to the CNN network, which acts as a feature extractor before entering the LSTM network. After various experiments, we determined the properties of the CNN networks. Both CNN networks (block CNN-1 and CNN-2 in
Figure 6) are composed of five convolutional layers and a single average pooling layer. The reshape layer configures the outputs produced by the CNN layers before entering the LSTM network. The same number of neurons are maintained from the previous experiment (15 neurons) with the rectified linear unit (ReLU) activation function. A dense layer with one neuron yields the final prediction. During the training process, the Adam optimiser was used. The properties of each layer are summarised in
Table 4.
As explained in
Section 4.2, we use eight samples to predict one future sample. To implement deeper convolutional layers as feature extractors to a relatively short data length (in our case, eight samples), we should set small kernel sizes. The length of the next convolutional layer can be calculated using Equation (
2). By setting a small value of kernel size
k, we can get higher output size
o. Thus, a small kernel size will give more possibilities to operate another convolutional layer in the next step. In our work, we use kernel size equal to 3 for the first and second convolutional layers and kernel size equal to 2 for remaining three convolutional layers. The selected kernel sizes and filters shown in
Table 4 are obtained based on our various experiments. Choosing a smaller filter size for each layer will produce a smaller final model size. Thus, it will benefit to our edge device. We found that the filter sizes of 50, 30, 15, 10 and 5 for each convolutional layer in our model produce the best result. We also discovered that the same properties of CNN-1 and CNN-2 yield optimum solutions as feature extractors while maintaining work balance for each input during training and inferencing stages.
4.4. Spatiotemporal Dependencies
In this study, both spatial and temporal qualities are studied. The temporal factor is taken into account by selecting time-lag data (lookbacks) as a model input, as discussed in
Section 4.2. A time lag equal to zero indicates the current sample. When the time-lag is less than 8, the autocorrelation coefficient is higher than 0.7 for all nodes. This autocorrelation value indicates a high temporal correlation. Therefore, we use eight values for the input length (current measured value plus seven past values).
As mentioned in
Section 4.3, in the first input of the model (INPUT-1), temporal dependency of the local node data is covered. The attributes involved for the first input are eight timesteps of PM
2.5, PM
10, SO
2, CO, NO
2, O
3, temperature, air pressure, dew point, wind direction and wind speed. We can consider that in INPUT-1, only temporal data are covered. However, in the second input of the model (INPUT-2), both temporal and spatial data of the local and pairing nodes are included. In the second input, we collect only eight timesteps of all PM
2.5 data (from local and surrounding nodes) and neglect all other environmental and meteorological data. All PM
2.5 samples from 12 nodes are analysed and the PM
2.5 correlation coefficients between nodes are calculated. Evaluating the correlation coefficient can indicate the effect of spatial dependency. As shown in
Table 5, PM
2.5 concentrations have a strong correlation (
) among nodes. A strong correlation implies that there is a high spatial dependency for PM
2.5 among nodes. Therefore, in this experiment, we include a feature extraction process for the PM
2.5 concentrations at all neighbouring nodes (data INPUT-2).
Figure 7 depicts the kinds of input data required to forecast the value of PM
2.5 at a certain node. If we want to forecast the next 1-h value of PM
2.5 concentration at Node 1, we need to use current pollutant and meteorological samples plus seven previous samples collected by that node (the first input of the proposed model) and collect all PM
2.5 values from all other nodes (the second input of the proposed model). This scenario also applies to all other nodes.
4.5. Deep Learning Data Processing
The properties of our proposed deep learning model are summarised in
Table 4. In this section, we discuss the internal inference process in our deep learning model. In CNN-1, the eight timesteps of 11 input features form an
matrix. These 11 features are composed of pollutant and meteorological data (PM
2.5, PM
10, SO
2, CO, NO
2, O
3, temperature, air pressure, dew point, wind direction and wind speed). In CNN-2, the eight timesteps of 12 input features form an
matrix. These 12 features consist of PM
2.5 concentrations at 12 nodes. According to Equation (
2), with a kernel (or feature detector) size of 3 and a stride step of 1, the kernel slides through the input matrix for six steps
. With a filter size of 50, the first convolutional layer yields a
matrix. In the second convolutional layer, the input is now a
matrix. With a size of 3, the kernel slides along the window for four steps
and produces a
matrix (since the filter size is 30). The same process applies to all convolutional layers. Thus, the fifth convolutional layer yields a
matrix. A global average pooling layer behaves as a flattening process. By concatenating both CNN layer outputs, the tensor is ready to enter the LSTM network. The LSTM network consists of 15 cells (or units). Details of the data processing inside an LSTM cell are discussed in
Section 3.2. Finally, a single dense layer produces the final result, i.e. our PM
2.5 prediction.
Figure 8 summarises this process.
4.6. The Selected Edge Devices
Having evaluated the proposed deep learning model, we now optimise and deploy that model to edge devices. In this work, we utilised the Raspberry Pi, a popular, credit card-sized yet powerful single-board computer developed by the Raspberry Pi Foundation. In recent years, there have been considerable varieties of applications developed using Raspberry Pi boards [
48]. We chose two different Raspberry Pi boards: Raspberry Pi 3 Model B+ (RPi3B+) and Raspberry Pi 4 Model B (RPi4B) to show the variation in model performance. The RPi4B is more computationally capable than the RPi3B+.
Table 6 shows a feature comparisons between the two boards.
We selected Raspberry Pis since these boards support both TensorFlow and TensorFlow Lite frameworks. Therefore, we can explore wide-range functionalities related to post-training quantisation provided by TensorFlow and demonstrate the performance of both original and quantised models by calculating the model accuracy, the obtained model file sizes and the execution time directly at the edge. Moreover, the Raspberry Pi’s rapid use for research and hobbyist purposes gave rise to many online forums and communities.
6. Conclusions
Edge computing brings computation closer to data sources (edge) and can be a solution for latency, privacy and scalability issues faced by a cloud-based system. It is also possible to embed intelligence at the edge, which can be enabled by Machine Learning algorithms. Deep Learning, a subset of ML, can be implemented at the edge. In this work, we propose a hybrid deep learning model composed of 1D Convolutional Neural Network and Long-Short Term Memory (CNN-LSTM) networks to predict a short-term hourly PM2.5 concentration at 12 different nodes. The results showed that our proposed model outperformed other possible deep learning models, evaluated by calculating RMSE and MAE errors at each node. To implement an efficient model for edge devices, we applied four different post-quantisation techniques provided by TensorFlow Lite framework: dynamic range quantisation, float16 quantisation, integer with float fallback quantisation and full integer-only quantisation. Dynamic range and float16 quantisations maintain model accuracy but did not improve latency significantly. Meanwhile, full integer quantisation outperformed other TFLite models in terms of model size and latency but slightly reduced model accuracy. The targeted edge devices in our work are the Raspberry Pi 3 Model B+ and Raspberry Pi 4 Model B boards. Technically, the Raspberry Pi 4 demonstrated lower latency due to the more capable processor.
In the future, we plan to develop this work further by offloading model computation for multiple nodes to a gateway device, thereby allowing the sensor nodes to be extremely lightweight. We would also like to explore methods for efficient sharing of a gateway deep learning model by multiple nodes. Finally, we would like to explore how models can be evolved on these edge devices.