A Multivariate Model for Coastal Water Quality Mapping Using Satellite Remote Sensing Images
Abstract
:1. Introduction
2. Study area and data collection
3. Remote sensing image analysis
- Lsλ= solar radiance reaching the sensor
- = the exoatmospheric solar irradiance
- Edλ = the downwelled irradiance from the sky dome onto the target
- Luλ= upwelled solar radiance
- θ = the view angle in the sensor-target direction
- σ = the sun angle in the sun-target direction
- ϕs = the azimuth angle in the sun-target direction
- ϕd = the azimuth angle in the sensor-target direction
- τ1(λ) = the atmospheric transmittance along the sun-target path
- τ2(λ) = atmospheric transmittance along the target-sensor path.
- λ = spectral wavelength of solar radiation
- ρ = spectral reflectance of the target surface
- F = the obstruction factor.
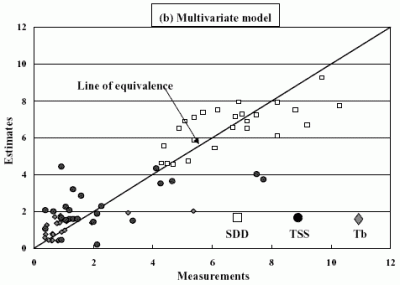
4. Water quality estimation
5. Water quality mapping
6. Conclusions
- (1)
- A surface reflectance estimation scheme which involves choosing a radiometric control area was proposed in this study. The scheme is applicable for local-scale environmental monitoring applications.
- (2)
- The three water quality variables (TSS, Tb and SDD) are found to be most related to the red band surface reflectance. High values of the sea surface reflectance generally correspond to high TSS and Tb concentrations and low SDD values.
- (3)
- The water body is a mixture of the seawater and other constituents including the suspended solids, the dissolved organic matters, the zooplankton, etc. The proposed multivariate water quality estimation model takes into consideration the wavelength-dependent combined effect of individual constituents on the sea surface reflectance and yields more accurate water quality estimation results.
- (4)
- Water quality mapping using remote sensing images shows a general pattern of increasing SDD and decreasing Tb and TSS outward from the coast. Under higher wave condition, water quality in the Yin-Yang Sea area may have more significant influence on the spatial distribution of water quality in the nearby area.
- (5)
- Until present, no significant effect of the diverted flow on coastal water quality has been observed due to few cases of flow diversion. However, a routine operation of coastal water quality mapping utilizing satellite images is recommended for assessment of the long term effect of the diverted flow.
Acknowledgments
References
- Lillesand, T.M.; Johnson, W.L.; Deuell, R.L.; Lindstorm, O.M.; Meisner, D.E. Use of Landsat data to predict the trophic state of Minnesota lakes. Photogramm. Eng. Remote S. 1983, 49, 219–229. [Google Scholar]
- Han, L. Spectral reflectance with varying suspended sediment concentrations in clear and algae-laden Waters. Photogramm. Eng. Remote S. 1997, 63, 701–705. [Google Scholar]
- Han, L.; Rundquist, D.C. Comparison of NIR/Red Ratio and First Derivative of Reflectance in Estimating Algal-Chlorophyll Concentration: A Case Study in a Turbid Reservoir. Remote Sens. Environ. 1997, 62, 253–261. [Google Scholar]
- Thiemann, S.; Kaufmann, H. Determination of chlorophyll content and trophic state of lakes using field spectrometer and IRS-1C satellite data in the Mecklenburg Lake District, Germany. Remote Sens. Environ 2000, 73, 227–235. [Google Scholar]
- Cheng, K.S.; Lei, T.C. Reservoir trophic state evaluation using Landsat TM images. J. Am. Water Res. Assoc. 2001, 37(5), 1321–1334. [Google Scholar]
- Giardino, C.; Pepe, M.; Brivio, P.A.; Ghezzi, P.; Zilioli, E. Detecting chlorophyll, Secchi disk depth and surface temperature in a sub-alpine lake using Landsat imagery. Sci. Total Environ. 2001, 268, 19–29. [Google Scholar]
- Kloiber, S.M.; Brezonik, P.L.; Olmanson, L.G.; Bauer, M.E. A procedure for regional lake water clarity assessment using Landsat multispectral data. Remote Sens. Environ 2002, 82, 38–47. [Google Scholar]
- Wang, Y.; Xia, H.; Fu, J.; Sheng, G. Water quality change in reservoirs of Shenzhen, China: detection using Landsat/TM data. Sci. total environ 2004, 328, 195–206. [Google Scholar]
- Tang, D.L.; Kester, D.R.; Ni, I.H.; Qi, Y.Z.; Kawamura, H. In situ and satellite observations of a harmful algal bloom and water condition at the Pearl River estuary in late autumn 1998. Harmful Algae 2003, 2, 89–99. [Google Scholar]
- Tang, D.L.; Kawamura, H.; Oh, I.S.; Baker, J. Satellite evidence of harmful algal blooms and related oceanographic features in the Bohai Sea during autumn 1998. Adv. Space Res. 2006, 37, 681–689. [Google Scholar]
- Shanmugam, P.; Ahn, Y.H.; Ram, P.S. SeaWiFS sensing of hazardous algal blooms and their underlying mechanisms in shelf-slope waters of the Northwest Pacific during summer. Remote Sens. Environ. 2008, 112, 3248–3270. [Google Scholar]
- Wei, G.F.; Tang, D.L.; Wang, S. Distribution of chlorophyll and harmful algal blooms (HABs): A review on space based studies in the coastal environments of Chinese marginal seas. Adv. Space Res. 2008, 41, 12–19. [Google Scholar]
- Bagheri, S.; Dios, R.A. Chlorophyll-a estimation in New Jersey's coastal waters using Thematic Mapper data. Int. J. Remote Sens. 1990, 11, 289–299. [Google Scholar]
- Khorram, S.; Cheshire, H.; Geraci, A.L.; Rosa, G.L. Water quality mapping of Augusta Bay, Italy from Landsat_TM data. Int. J. Remote Sens. 1991, 12, 803–808. [Google Scholar]
- Ekstrand, S. Landsat TM based quantification of chlorophyll-a during algae blooms in coastal waters. Int. J. Remote Sens 1992, 13, 1913–1926. [Google Scholar]
- Lavery, P.; Pattiaratchi, C.; Wyllie, A.; Hick, P. Water quality monitoring in estuarine waters using the Landsat Thematic Mapper. Remote Sens. Environ. 1993, 46, 268–280. [Google Scholar]
- Tassan, S. An improved in-water algorithm for the determination of chlorophyll and suspended sediment concentration from Thematic Mapper Data in coastal waters. Int. J. Remote Sens. 1993, 14(6), 1221–1229. [Google Scholar]
- Pattiaratchi, C.; Lavery, P.; Wyllie, A.; Hick, P. Estimates of water quality in coastal waters using multi-date Landsat Thematic Mapper data. Int. J. Remote Sens. 1994, 15, 1571–1584. [Google Scholar]
- Lin, I.I.; Wen, L.S.; Liu, G.R.; Liu, K.K. Retrieval of suspended particulate matter and chlorophyll-a concentration in a highly turbid tropical river by in situ bio-optical data – a case study. Photogramm. Eng. Remote S. 2002, 7, 75–85. [Google Scholar]
- Gin, K.Y.H.; Koh, S.T.; Lin, I.I. Spectral irradiance profiles of suspended marine clay for the estimation of suspended sediment concentration in tropical waters. Int. J. Remote Sens. 2003, 24(16), 3235–3245. [Google Scholar]
- Oyama, Y; Matsushita, B.; Fukushima, T.; Nagai, T.; Imai, A. A new algorithm for estimating chlorophyll-a concentration from multi-spectral satellite data in case II waters: a simulation based on a controlled laboratory experiment. Int. J. Remote Sens. 2007, 28(7), 1437–1453. [Google Scholar]
- Tomascik, T.; Sander, F. Effects of eutrophication on reef-building corals. I. Growth rate of the building coral Montastrea annularis. Mar. Biol. 1985, 87, 143–155. [Google Scholar]
- Hoegh-Guldberg, O.; Muscatine, L.; Goiran, C.; Siggaard, D.; Marion, G. Nutrient-induced perturbations to δ13C and δ15N in symbiotic dinoflagellates and their coral hosts. Mar. Ecol. Prog. Ser. 2004, 280, 105–114. [Google Scholar]
- Koponen, S.; Pulliainen, J.; Kallio, K.; Hallikainen, M. Lake water quality classification with airborne hyperspectral spectrometer and simulated MERIS data. Remote Sens. Environ. 2002, 79, 51–59. [Google Scholar]
- Schott, J.R. Remote Sensing; Oxford University Press: New York, USA, 1997; p. 394. [Google Scholar]
- Teng, S.P.; Chen, Y.K.; Cheng, K.S.; Lo, H.C. Hypothesis-test-based landcover change detection using multitemporal satellite images. Adv. Space Res. 2008, 41, 1744–1754. [Google Scholar]
- Chavez, P.S., Jr. An improved dark-object subtraction technique for atmospheric scattering correction of multispectral data. Remote Sens. Eenviron. 1988, 24, 459–479. [Google Scholar]
- Khorram, S. Water quality mapping from Landsat digital data. Int. J. Remote Sens. 1981, 2, 145–153. [Google Scholar]
- Khorram, S. Remote sensing of water quality in the Neuse River Estuary, North Carolina. Photogramm. Eng. Remote S. 1985, 51, 329–341. [Google Scholar]
- Rimmer, J.C.; Collins, M.B.; Pattiaratchi, C.B. Mapping of water quality in coastal waters using airborne thematic mapper data. Int. J. Remote Sens. 1987, 8, 85–102. [Google Scholar]
- Tassan, S. Evaluation of the potential of the thematic mapper for marine application. Int. J. Remote Sens. 1987, 8, 1455–1478. [Google Scholar]
- Ritchie, J.C.; Cooper, C.M. Comparison of measured suspended sediment concentrations with suspended sediment concentrations estimated from Landsat MSS data. Int. J. Remote Sens. 1988, 9(3), 379–387. [Google Scholar]
- Prangsma, G.J.; Roozekrans, J.N. Using NOAA AVHRR imagery in assessing water quality parameters. Int. J. Remote Sens. 1989, 10, 811–818. [Google Scholar]
- Populus, J.; Hastuti, W.; Martin, J.L.M.; Guelorget, O.; Sumartono, B.; Wibowo, A. Remote sensing as a tool for diagnosis of water quality in Indonesian seas. Ocean Coast. Manag. 1995, 27, 197–215. [Google Scholar]
- Härmä, P.; Vepsäläinen, J.; Hannonen, T.; Pyhälahti, T.; Kämäri, J.; Kallio, K.; Eloheimo, K.; Koponen, S. Detection of water quality using simulated satellite data and semi-empirical algorithms in Finland. Sci. Total Environ. 2001, 268, 107–121. [Google Scholar]
- Doxaran, D.; Froidefond, J.M.; Lavender, S.; Castaing, P. Spectral signature of highly turbid waters – Application with SPOT data to quantify suspended particulate matter concentrations. Remote Sens. Environ 2002, 81, 149–161. [Google Scholar]
- Cannizzaro, J.P.; Carder, K.L. Estimating chlorophyll a concentrations from remote-sensing reflectance in optically shallow waters. Remote Sens. Environ 2006, 101, 13–24. [Google Scholar]
- Dunteman, G.H. Introduction to Multivariate Analysis; Sage Publications: Beverly Hills, CA, 1984; p. 237. [Google Scholar]











| Sampling date | SPOT image acquisition date | Relevant storm events | Volume of diverted flow (m3) |
|---|---|---|---|
| 7/02/2007 | 7/04/2007 (SPOT-4) | No storm | 0 |
| 7/18/2007 | 7/19/2007 (SPOT-4) | No storm | 0 |
| 8/15/2007 | NAa | No storm | 0 |
| 8/23/2007 | 8/23/2007 (SPOT-5) | Typhoon Sepat (8/16∼8/19) | 0 |
| 9/07/2007 | 9/03/2007 (SPOT-5) | No storm | 0 |
| 9/20/2007 | NAa | Typhoon Wiphab (9/17∼9/19) | 1,051,200 |
| 10/08/2007 | NA | Typhoon Krosab (10/4∼10/7) | 16,133,400 |
| 11/14/2007 | NA | No storm | 0 |
| Mean | Standard deviation | Maximum | Minimum | |
|---|---|---|---|---|
| Secchi disk depth (m) | 5.39 | 2.11 | 10.30 | 0.50 |
| Turbidity (NTU) | 2.19 | 4.19 | 29.50 | 0.38 |
| Total suspended solid (mg/L) | 4.79 | 5.95 | 30.61 | 0 |
| Image acquisition date | Reflectance calibration ratio | ||
|---|---|---|---|
| Green | Red | Near infrared | |
| 7/04/2007 | 0.00282 | 0.00313 | 0.00420 |
| 7/19/2007 | 0.00232 | 0.00249 | 0.00410 |
| 8/23/2007 | 0.00331 | 0.00336 | 0.00532 |
| 9/03/2007 | 0.00345 | 0.00342 | 0.00500 |
© 2008 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Su, Y.-F.; Liou, J.-J.; Hou, J.-C.; Hung, W.-C.; Hsu, S.-M.; Lien, Y.-T.; Su, M.-D.; Cheng, K.-S.; Wang, Y.-F. A Multivariate Model for Coastal Water Quality Mapping Using Satellite Remote Sensing Images. Sensors 2008, 8, 6321-6339. https://doi.org/10.3390/s8106321
Su Y-F, Liou J-J, Hou J-C, Hung W-C, Hsu S-M, Lien Y-T, Su M-D, Cheng K-S, Wang Y-F. A Multivariate Model for Coastal Water Quality Mapping Using Satellite Remote Sensing Images. Sensors. 2008; 8(10):6321-6339. https://doi.org/10.3390/s8106321
Chicago/Turabian StyleSu, Yuan-Fong, Jun-Jih Liou, Ju-Chen Hou, Wei-Chun Hung, Shu-Mei Hsu, Yi-Ting Lien, Ming-Daw Su, Ke-Sheng Cheng, and Yeng-Fung Wang. 2008. "A Multivariate Model for Coastal Water Quality Mapping Using Satellite Remote Sensing Images" Sensors 8, no. 10: 6321-6339. https://doi.org/10.3390/s8106321
APA StyleSu, Y. -F., Liou, J. -J., Hou, J. -C., Hung, W. -C., Hsu, S. -M., Lien, Y. -T., Su, M. -D., Cheng, K. -S., & Wang, Y. -F. (2008). A Multivariate Model for Coastal Water Quality Mapping Using Satellite Remote Sensing Images. Sensors, 8(10), 6321-6339. https://doi.org/10.3390/s8106321