Take Profit and Stop Loss Trading Strategies Comparison in Combination with an MACD Trading System

Abstract

A lot of strategies for Take Profit and Stop Loss functionalities have been propounded and scrutinized over the years. In this paper, we examine various strategies added to a simple MACD automated trading system and used on selected assets from Forex, Metals, Energy, and Cryptocurrencies categories and afterwards, we compare and contrast their results. We conclude that Take Profit strategies based on faster take profit signals on MACD are not better than a simple MACD strategy and of the different Stop Loss strategies based on ATR, the sliding and variable ATR window has the best results for a period of 12 and a multiplier of 6. For the first time, to the best of our knowledge, we implement a combination of an adaptive MACD Expert Advisor that uses back-tested optimized parameters per asset with price levels defined by the ATR indicator, used to set limits for Stop Loss.

1. Introduction

When trading on an asset, investors are exposed to a potentially high risk if the price moves towards a direction which is the opposite from the one they had anticipated. This could result in considerable losses in the investment capital, unless immediate action is taken to exit the non-profitable position as soon as possible. On the other hand, if the price moves towards a direction that makes the current position profitable, an investor might want to close the position and cash in the profits gained so far, as there is always the possibility that winning trades could turn into losing positions and lead to catastrophic losses.

Different strategies of securing profits (Take Profit) and averting losses (Stop Loss) have been proposed and examined, usually involving the prices at which a position was opened, and are frequently used by traders, as well as automated trading systems. In this research, we tested and compared six different Take Profit and Stop Loss strategies used in combination with an algorithmic trading system, based on the MACD indicator on eleven different assets over a six-month period. With the results of these comparisons, we aim to provide some practical insights into every day traders about which Take Profit and Stop Loss technics to incorporate with an existing MACD strategy and which to avoid. There have been numerous studies about MACD, which is a 30-year-old tool, such as those by Chong and Ng (2008) and Yazdi and Lashkari (2013), focused on MACD’s performance in various markets and timeframes, or such as that by Ni and Yin (2009), who examined, among others, Take Profit and Stop Loss technics in MACD using neural networks. But there has not yet been a study of MACD combined with the Take Profit/Stop Loss strategies we examined based on ATR and in a faster timeframe.

2. Materials and Methods

2.1. Trading Systems

2.1.1. Automated Trading

Nowadays, trading is almost exclusively conducted electronically through a computer (Jain 2005). In addition to that, investors have replaced the broker with a platform of automated trading (algorithmic trading), as was postulated by Hendershott and Moulton (2007).

The decrease in the cost of this technology has led to its fast-paced adoption by the financial industry. The resulting technological change has brought about a revolution in the financial markets and the way the assets are traded. Many institutions today trade through algorithms and algorithmic trades improve liquidity. It has been proven that the increased algorithmic trades limit wrong price choices and decrease the proportion of offer risk over different price levels of an asset associated with the trades. These results show that algorithmic trading lowers the cost of trades and enhances the informativeness of quotes, as demonstrated by Hendershott et al. (2011).

On the other hand, it seems that Forex manual trading outweighs automated trading systems. Humans are more informed than systems (Chaboud et al. 2014). However, on closer inspection, we realize that there are some indications pointing to the fact that algorithmic trading contributes to an efficient price discovering process (Brogaard et al. 2014) through the elimination of opportunities for triangular arbitrage and faster “integration” of macroeconomic news into the price (Foucault et al. 2011). Also, in the same paper, it was established that algorithmic trades tend to correlate, demonstrating that automated strategies are not that different from those used by a human. Despite that correlation, there are no indications that algorithmic trading causes excess variability. In addition, the volume of algorithmic trading in the market has a small, but positive, impact on the liquidity of the market.

In this research, only algorithmic trades are executed without human intervention, with an automated high frequency trading system. Consequently, commissions and the cost of position swap are kept to a minimum, in contrast with using human intermediaries, and are subsequently presented. But the main element is the fact that they are automatically included in the results by the trading terminal we used. Consequently, the profit rate presented in this paper is pure, after the deduction of commissions.

2.1.2. Private Investors

As more brokers adopt electronic trading platforms, more private investors opt for automated algorithmic trading. It is estimated that private investors lose 2% in the USA market and 3.8% in Taiwan annually (Barber et al. 2008). It has also been calculated that institutional profits are enhanced by 1.5% annually as a result of the small transactions’ cost and corresponding profits of the same actions.

The feeling of the individual investors in relation to weekly and monthly profits and the variability of NYSE stocks was studied by Kaniel et al. (2004). Private investors who are more aware of the risk may force them to provide liquidity to other market participants who seek an instant service. The buying orders from bigger, stock-accumulating investors can cause a coercion of sales by increasing the prices. In the same way, individual buyers are attracted to lower prices caused when these larger investors choose to sell their stocks. Liquidity is actually provided by both professional traders (e.g., specialists) and individuals. If we assume that market liquidity is only provided by individual investors and they are more active in relation to the demand for immediacy, then there would be an excess supply of liquidity. In this case, individual investors that have contracts and are silent liquidity providers will amount losses, while more terms-informed investors will perform trades in adverse conditions. If, on the other hand, there are fewer investors than the market immediacy demands, the silent liquidity providers will amount profits. Understanding the predictability of the short-term profits calls for an understanding of the silent liquidity provision to individuals, as well as the explicit liquidity provision to professional investors. Specifically, the provision of liquidity can be regarded as the interaction between different types of investors that trade on the same market.

A lot of individuals, in parallel with these systems, adopt long-term positions, instead of strategic buying and holding, strategies whose trends are reflected on Google Trends, an analysis by Preis et al. (2013) quantifying the behavior of the market. In this research, there is no liquidity problem, especially for the $10,000 of initial capital, as the automated systems tested in this research can be implemented by institutes, as well as by private investors. On the other hand, it has been proven through back-testing that whether or not data from the profits of an asset or data from Google Trends are used for the same asset, the results are the same. The results have been tested on a non-linear machine learning system by Challet and Ayed (2014). In the current work, the problem of back-testing period selection is evident.

2.2. Take Profit & Stop Loss

Returns can be either absolute or relative. As a rule, we avoid absolute numbers because they will have to be calculated for each asset individually. Leung and Li (2015) proved that the stop loss function has to be calculated at every moment because it is related to the price of an asset at every tick since that price is within the price range x ∈ (L, b × L), or the investor, if x is the entering price, can simply set a constant I (proportional to the fluctuation we add), where x−I is the stop loss price. In addition, returns change over seasons and periods, according to the influences an asset undergoes as a result of outside or inside factors. It is obvious that orders with stop loss and take profit, when activated, oppose the market trend (take profit) or intensify the movement (stop loss), with great influence even over the liquidity during a flash crash (Easley et al. 2011). In all these adoptive trading systems, special consideration should be given to the use of these functions, as shown by Austin et al. (2004). In addition, the use of cut-loss orders and take profit orders and the range of these orders reflect the risk-taking desire of the investor (Au et al. 2003).

With regard to absolute numbers, we see a 3% take profit and a 2% stop loss in the work by Bolgün et al. (2010) on stocks of the Istanbul Stock Exchange. Constant take profit was used by Krishnan and Menon (2009), defined at 20 pips, in an interesting work that examined the influence that rate, closing price times, and indicators participating in trading systems (RSI, BB, Stoch, SAR, MACD, ADX, CCI, Williams %R, Mom, A/D) have on profit. Take profit was also set at 20 pips by Barbosa and Belo (2010). Even in systems that are based on the flow of buy and sell orders and not on the price itself, as postulated by Bates et al. (2003), stop loss and take profit were used as a function of returns 0–0.5%, 0.5–1%, etc. Similarly, Azzini and Tettamanzi (2008b) set staggering take profit signals on returns of 0.33%, 0.67%, etc., while in another work, Azzini and Tettamanzi (2008a) took three returns as take profit, logarithmically setting the constant at rTP = 0.006, 0.008, or 0.0046. Martinez et al. (2009) conducted experiments that converted the percentage of loss break from 0.1% to 2.0%. A small loss break percentage could impede profitable transactions, while a high one could cause bigger losses. The system executes more profitable transactions with the stop loss rules and the 0.5% percent yielded the best results.

As for the fluctuation range, we consider that take profit and stop loss functions display flexibility of profitability adjusted on each asset. In this way, with the range (R), stop loss = 0,5R and take profit = 1R were set by Cervelló-Royo et al. (2015). It is obvious that profit>stop loss is the only fair deal. Consequently, we make sure that 1R > 0.5R. Klement (2013) set the stop loss (c) in combination with a reentry condition (d), where (c) as the stop loss level is expressed in units of annual standard deviation of the return of an asset. The same applies for (d). Similarly, Chevallier and Ielpo (2012) set a dynamic stop loss and reduced the losses on S&P500, for which the rule is as follows: if the proposed rate of return against the variability reaches a lower limit (n), that is, the number of fluctuation days of the market that will activate the stop loss rule, then this is a signal for the selling of the investment.

We prove here that the addition of take profit and stop loss could considerably improve the results, to the point that they become profitable, in contrast to the claim laid by Clare et al. (2013). More specifically, this became more evident after the proof put forward by Han et al. (2016), who, with a stop loss at 10% of the monthly returns of a strategy based on the momentum, achieved a reduction of losses from −49.79% to −11.36%. Likewise, for monthly data from 1950 to 2004 setting stop loss on American long-term bonds investment, Kaminski and Lo (2014), improved the return over the buying and holding strategy by 50–100 basis points.

Lei and Li (2009) applied a constant price stop loss, as well as trailing stop loss, for stocks of NYSE and AMEX from 1970 to 2005. They concluded that the stop loss function shields investors from holding a non-profitable position for a long period of time, which could result in big losses of capital. On the other hand, they found a distinction between the profits’ enhancement and the risk reduction. The analysis of exchange rates of high frequency by Osler (2005) yields facts that provide support for the idea that orders of stop loss have an influence on the fall of prices. First of all, the change in exchange rates is faster when the prices reach levels at which stop loss orders are usually placed. Secondly, the effect of stop loss orders is greater than the effect of the take profit orders, which also helps the fast changes in prices by creating an opposite trend. Thirdly, the effect of stop loss orders has a broader time duration than that of take profit orders.

All of the above stop loss and take profit rules and conditions can be evaluated and sorted with regard to the profitability of the investment through a number of ways, where the aggregate profit would be the ultimate result, but with an evaluation framework proposed by Chan and Ma (2015).

The take profit and stop loss functions we use and analyze below are dynamic, follow the average fluctuation and the current price for every tick, and are activated instantaneously.

2.3. Automated Trading Strategy Development and Combinations

For this research, we used an automated trading system (Expert Advisor) based on the MACD indicator. We started with a simple system and progressively added more complex features, implementing Take Profit and Stop Loss functionalities.

2.3.1. The MACD Indicator and Expert Advisor

The MACD (Moving Average Convergence/Divergence) is a well-known indicator created in 1979 by Appel (2005). It calculates the difference of two exponential moving averages of different periods over a time-series. The moving average with the smaller period is called the fast moving average and the moving average with the bigger period is called the slow moving average.

$$\mathrm{MACD} \mathrm{line}={\mathrm{EMA}}_{p_{fast}}\left(\mathrm{Timeseries}\right)-{\mathrm{EMA}}_{p_{slow}}\left(\mathrm{Timeseries}\right),p_{fast}<p_{slow}$$

(1)

Another exponential moving average is calculated on the MACD line, called the Signal line:

$$\mathrm{Signal}\mathrm{line}={\mathrm{EMA}}_{p_{signal}}\left(\mathrm{MACD}\mathrm{line}\right)$$

(2)

When the MACD line is above the Signal line, this is an indication of an upward trend momentum in the time-series and when the MACD line is below the Signal line, this is an indication of a downward trend momentum in the time-series.

The default values of the three periods used in the calculations of the MACD indicator are usually $p_{fast}=12$, $p_{slow}=26$, and $p_{signal}=9$ in the daily timeframe. An example of the MACD indicator can be seen in Figure 1.

An automated trading system (Expert Advisor) can be formulated on the basis of the MACD indicator following the rules below:

When the MACD line crosses above the Signal line, this constitutes a buy signal and any short positions are closed and a long position is opened.

When the MACD line crosses below the Signal line, this constitutes a sell signal and any long positions are closed and a short position is opened.

The abovementioned trading strategy in the form of a pseudocode can be found in Appendix A.

2.3.2. The MACD Expert Advisor with a quicker Take Profit Signal

Sometimes, the rate of change of a time-series can be more rapid than the rate at which the MACD indicator can provide us with a signal. If a position was open during that time, even if it was a successful one up until that moment, potential profits could be diminished and never materialize or even turn into losses.

A potential solution to that problem is the use of a different Signal line to judge when to exit a position, with a faster (smaller) period than that of the normal Signal line:

$$\mathrm{Take}\mathrm{Profit}\mathrm{Signal}\mathrm{line}={\mathrm{EMA}}_{p_{take profit signal}}\left(\mathrm{MACD}\mathrm{line}\right)$$

(3)

where

$$p_{take profit signal}=\frac{p_{signal}}{\mathrm{N}},\mathrm{N}=2, 3, \dots$$

(4)

An example of the MACD indicator with a Take Profit Signal Line can be seen in Figure 2.

Now, the Expert Advisor, in addition to the two previous rules, closes any long positions when the MACD line crosses below the Take Profit Signal line and any short positions when the MACD line crosses above the Take Profit Signal line. After that and until the next time, the MACD line crosses the Signal line, and no position is open, in contrast with the previous strategy, where there was always a long or a short position open. The abovementioned trading strategy in the form of a pseudocode can be found in Appendix A.

2.3.3. The MACD Expert Advisor with Signal Lines’ Hierarchy

There can be time periods when the time-series of an asset does not follow a clear upward or downward trend, but instead oscillates around a value. During these periods, the previous strategies produce a lot of signals and change positions frequently, which can potentially lead to losses, because there is not enough time for the price to move to profitable levels and every transaction and position change comes at a cost. A more effective option might involve staying out of the market during these periods and only opening a new position when clear upward or downward trends occur.

The clarity of a trend can be judged by means of the MACD, Signal, and Take Profit Signal lines. When the prevailing trend is bullish, then we have the MACD line above the Take Profit Signal line and the Take Profit Signal line above the Signal line. Likewise, when the trend is bearish, we have the MACD line below the Take Profit Signal line and the Take Profit Signal line below the Signal line.

The Expert Advisor still closes positions using the Take Profit Signal line in the same way as in the previous case, but only opens new positions if the hierarchy of the MACD, Take Profit Signal, and Signal lines matches the one outlined in the above paragraph. The abovementioned trading strategy in the form of a pseudocode can also be found in Appendix A.

2.3.4. The Average True Range Indicator

The Average True Range or ATR indicator is a measure of volatility introduced in 1978 by Wilder (1978). The True Range for a specific interval is defined as

$$\mathrm{TR}=\max \left[\left(\mathrm{high}-\mathrm{low}\right),\mathrm{abs}\left(\mathrm{high}-{\mathrm{close}}_{\mathrm{prev}}\right),\mathrm{abs}\left(\mathrm{low}-{\mathrm{close}}_{\mathrm{prev}}\right)\right]$$

(5)

The ATR of period N is calculated as

$$\mathrm{ATR}=\frac{1}{\mathrm{N}}{\displaystyle \sum }_{i=1}^{\mathrm{N}}{\mathrm{TR}}_i$$

(6)

for the first instance and after that as

$${\mathrm{ATR}}_t=\frac{{\mathrm{ATR}}_{t-1}\times \left(\mathrm{N}-1\right)+{\mathrm{TR}}_t}{\mathrm{N}}$$

(7)

2.3.5. The MACD Expert Advisor combined with the ATR Indicator for Stop Loss Strategies

The ATR indicator can be used to set a Stop Loss barrier when a new position is opened following an MACD Expert Advisor signal. When the MACD Expert Advisor opens a new long position, a Stop Loss barrier can be set at

$$\mathrm{Stop}\mathrm{Loss}\mathrm{Barrier}=\mathrm{Opening}\mathrm{Price}-x\times \mathrm{ATR}\left(\mathrm{N}\right)$$

(8)

where Opening Price is the price the long position was opened at, ATR(N) is the value of the ATR indicator of period N at that moment, and x is a constant multiplier used to adjust the barrier’s width. When the asset’s price moves below that barrier, the long position is closed.

Likewise, when a short position is opened, a Stop Loss barrier can be set at

$$\mathrm{Stop}\mathrm{Loss}\mathrm{Barrier}=\mathrm{Opening}\mathrm{Price}+x\times \mathrm{ATR}\left(\mathrm{N}\right)$$

(9)

When the asset’s price moves above this barrier, then the short position is closed.

After a Stop Loss is triggered and a position closed, it is possible that the MACD indicator keeps signaling for the same type of position to be opened. To avoid the immediate reopening of the same type of position after a Stop Loss, a new barrier can be created in the same way. Until the price moves above

$$\mathrm{New}\mathrm{Position}\mathrm{Barrier}=\mathrm{Closing}\mathrm{Price}+y\times \mathrm{ATR}\left(\mathrm{N}\right)$$

(10)

a long signal will not result in a new long position after a Stop Loss, and until the price moves below

$$\mathrm{New}\mathrm{Position}\mathrm{Barrier}=\mathrm{Closing}\mathrm{Price}-y\times \mathrm{ATR}\left(\mathrm{N}\right)$$

(11)

a short signal will not result in a new short position after a Stop Loss. The y parameter is a constant multiplier used to adjust the barrier’s width, as is the case with x. Examples of Stop Loss Barriers and New Position Barriers can be seen in Figure 3. The abovementioned trading strategy in the form of a pseudocode can also be found in Appendix A.

2.3.6. The MACD Expert Advisor with sliding ATR barrier zone

The ATR Stop Loss barriers described in the above section are drawn around the price at which a new position is opened and stay fixed, even if the price follows an upward, profitable trend, until there is a new MACD signal or the price moves back to the barrier.

In the second case, when the price moves back to the Stop Loss barrier, the potential gains from the previous profitable movements are never materialized. To prevent this, the ±x × ATR(N) zone can be redrawn each time the price moves out of it and follows a profitable direction. This slides the Stop Loss barrier to values that secure some of the profits gained so far.

On the other hand, the position prevention barrier should stay at the same level and not slide, as it could prevent the Expert Advisor from opening a new position for a long time. An example of this strategy can be seen in Figure 4.

2.3.7. The MACD Expert Advisor with sliding and variable ATR barrier zone

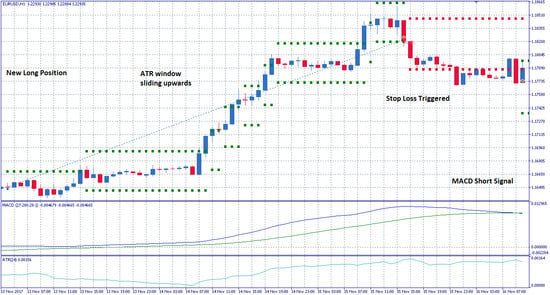
An asset’s price can show large or small variability as it changes over time, which reflects the value of ATR. In the previous cases, ATR barriers were of a constant range, calculated with the ATR value at the moment when a position opened. Using the latest ATR value to form an ATR window with a variable range through time, could prevent the expert advisor from exiting a position prematurely in periods when variability spikes and help him follow the price trends, as seen in Figure 5.

2.4. Data and Implementation

We conducted our experiments on the different Take Profit – Stop Loss strategies for nine assets from the Forex, Metals, Commodities, Energy, and Cryptocurrencies categories: AUDUSD, EURGBP, EURUSD, GBPUSD, USDCHF, USDJPY, XAUUSD, OIL, and BTCUSD. This choice mainly came from the need for assets that are traded on global markets on a 24 h base (or close to 24 h), as we wanted to examine the automated trading systems in a High Frequency Trading mode (hourly timeframe). The MACD Indicator has mainly been used for stock trading, but we opted to not trade stocks as the relatively big time intervals that exist between their trade sessions, in combination with the multinational activities of most of these corporations, can cause a lot of gaps and noise in their prices. The period we examined was from 3 September 2017 to 24 February 2018 with historical data from FXTM, GEBINVEST, and OctaFX. Because our systems were used in High Frequency Trading mode, we determined that a six-month period would be enough to draw conclusions about their performance.

For the testing, we used the Metatrader 5 trading terminal from Metaquotes, and Microsoft SQL Server for the initial data processing.

We set the initial test amount at $10,000 at a 1:100 leverage ratio for all assets except for BTCUSD, whose high price and spread required an equally high margin on the broker we used, so we set the initial amount at $10,000,000 and adjusted the results in such a way as to be comparable to the other assets. For each new position the automated trading system opens, it risks 20% of its current balance and no capital is deposited or withdrawn for the six-month period apart from the initial capital. The spreads for every asset (in pips) as reported by the brokers used were AUDUSD:0.7, EURGBP:0.6, EURUSD:0.4, GBPUSD:0.7, USDCHF:0.9, USDJPY:0.5, XAUUSD:21.0, OIL:5.0, and BTCUSD:11.5. The Metatrader 5 trading terminal also automatically adds the cost of each transaction to the Gross Losses so the Net Profits represent the actual pure number a trader has won or lost at the end.

2.4.1. Back testing Limitations

The Metatrader 5 terminal offers the ability to test an automated trading system over a past time period with various methods for simulating the price changes, such as every tick, every open-high-low-close value, every open value for a specific timeframe, etc. It also offers the ability to test a rage of the parameters used by the Expert Advisor in order to identify the best combination of parameters for a back testing period. In order to speed up back-tests, Metatrader 5 also offers the ability to use distributed testing agents utilizing the resources of a local network of computers. We used this ability to form a local cluster of computers, mainly with i5, i7, and Xeon Intel CPUs for a total capacity of 130 distributed agents, in order to run our backtesting experiments. We also used a Microsoft SQL Server in order to save and process the results of our experiments during the stage of parameter selection.

It should be noted that the wider the parameters’ ranges, the greater the number of combinations of parameters. Also, back testing with an every tick simulation is far more time- and resource-consuming than back testing with open-high-low-close value, which is in turn more time-consuming than an open value only simulation.

The values of the MACD and ATR indicators are calculated over one-hour timeframes, but during an hourly timeframe, the price of an asset can reach levels that would trigger a Take Profit/Stop Loss in some strategies or an automatic Stop Loss from the broker, so we chose to run our experiments with every tick simulations.

2.4.2. Parameter Selection

For our tests, we had to choose a set of parameters for each asset that would allow for the demonstration of an improvement or worsening in the MACD Expert Advisor’s behavior with the introduction of each Take Profit/Stop Loss strategy.

Since the different periods in the MACD averages can generate widely different results and in order to render the role of these parameters less significant for our tests, we decided to choose sets of parameters that are centered on neighborhoods (±2) of similar results, with the results indicating there is room for both improvement and worsening.

The simple MACD Expert Advisor has three parameters, the periods of its moving averages, which means that even for small parameter ranges, the number of combinations is significant. Performing a back test for every asset with full parameter sweeping on an every tick simulation would be prohibitive because of the time and electrical energy it would require. We circumvented this firstly by running the simulations on open-high-low-close prices ticks, which produces results close enough to the real tick simulation, and secondly by incrementing each parameter by a step of 2 instead of 1, which reduces the combinations to 1/8, allowing us to check a wider range. Potentially suitable neighborhoods can still be identified as a step of 2 still hits a ±2 neighborhood in eight or 27 of its 125 members.

Next, we defined some requirements for a suitable neighborhood, such as a minimum amount of trades and profit range, and chose the best 100 neighborhoods that fulfilled them, sorted by the smallest relative range defined as

$$\mathrm{Relative}\mathrm{Range}=\frac{\max \left(\mathrm{Profits}\right)-\min \left(\mathrm{Profits}\right)}{\mathrm{average}\left(\mathrm{Profits}\right)}$$

(12)

The specific requirements for each asset can be seen in

Table 1. Requirements set for neighborhood selection for each asset.

	Profits ∈	Trades≥	Central Value
AUDUSD	[0, 22500]	59
EURGBP	[−2800, 10800]	75
EURUSD	[1500, 6500]	75	MinProfit < 4000 < MaxProfit
GBPUSD	[0, 8500]	75	MinProfit < 4000 < MaxProfit
USDCHF	[400, 7600]	75	MinProfit < 4000 < MaxProfit
USDJPY	[200, 7800]	75	MinProfit < 4000 < MaxProfit
XAUUSD	[0, 1300]	75	MinProfit < 400 < MaxProfit
OIL	[0, 30000]	70
BTCUSD	[0, 220]	75

.

To be more certain, we ran back tests with every tick value for these 100 neighborhoods of each asset, with range ±2 around their center with step 1. The missing combinations changed the min, max and average profits of the neighborhoods, which resulted in changes in their order of classification. Finally, we conducted a supervisory review of the best options and chose a neighborhood for each asset that seemed the most fitting one and served our purposes. The final parameters are presented in

Table 2. Final parameters chosen for each asset and characteristics of their neighborhoods.

	Fast	Slow	Signal	MinProfit	MaxProfit	AvgProfit	Relative Range	MinTrades
AUDUSD	57	284	34	3693.40	8969.10	5918.32	0.8914	59
EURGBP	27	118	6	−672.23	4324.72	1274.10	3.9220	135
EURUSD	27	280	28	2403.46	6166.85	4210.10	0.8939	79
GBPUSD	15	82	14	1063.08	8268.69	4648.14	1.5502	129
USDCHF	29	132	22	736.39	6780.59	4161.61	1.4524	80
USDJPY	33	64	32	1702.63	5914.10	3545.61	1.1878	86
XAUUSD	17	160	16	240.32	1230.11	792.88	1.2484	108
OIL	51	60	34	5537.31	21058.19	12217.25	1.2704	76
BTCUSD	53	210	14	48.46	219.93	143.53	1.1946	77

.

3. Results and Discussion

3.1. Default/Selected Parameters and Weekends

Firstly, we compared the results for a) the simple MACD Expert Advisor with the default parameters $p_{fast}=12$, $p_{slow}=26,$ and $p_{signal}=9$ and without holding positions over weekends; b) the simple MACD Expert Advisor with our selected parameters and without holding positions over weekends; and c) the simple MACD Expert Advisor with our selected parameters with holding open positions over the weekends. Although the default MACD parameters refer to the daily timeframe, attempting to express two weeks, one month, and 1.5 weeks, respectively, we opted to keep them the same in the hourly timeframe instead of using the equivalent $p_{fast}=288$, $p_{slow}=624$, and $p_{signal}=216$ of days expressed in hours since that would move the scale outside the HFT. By porting the default parameters to the hourly timeframe, they then expressed ½ of a day, one day, and one work-day, which is closer to the timeframe of a daily trader doing HFT. The results of these three experiments can be seen in

Table A1. Results of experiments (a), (b), and (c).

	Gross Profits			Gross Losses			Net Profits
	a	b	c	a	b	c	a	b	c
AUDUSD	13,966.24	37,297.78	31,166.56	−23,816.08	−30,282.34	−24,627.67	−9849.84	7015.44	6538.89
EURGBP	22,526.94	54,321.39	49,798.47	−31,113.62	−55,099.62	−50,929.09	−8586.68	−778.23	−1130.62
EURUSD	45,671.48	36,106.59	32,522.98	−52,901.34	−31,757.62	−27,630.16	−7229.86	4348.97	4892.82
GBPUSD	56,474.11	48,025.86	44,737.63	−64,529.80	−45,705.37	−43,091.59	−8055.69	2320.49	1646.04
USDCHF	18,662.64	27,822.32	19,855.93	−28,019.51	−24,060.67	−18,962.81	−9356.87	3761.65	893.12
USDJPY	20,697.02	27,060.23	14,940.23	−30,106.48	−22,931.07	−17,282.76	−9409.46	4129.16	−2342.53
XAUUSD	17,208.71	9107.39	9749.19	−16,773.68	−8800.84	−8564.85	435.03	306.55	1184.34
OIL	9098.18	81,584.58	57,452.95	−19,058.36	−73,261.17	−55,665.34	−9960.18	8323.41	1787.61
BTCUSD	3297.66	2410.97	2462.69	−4681.72	−2404.57	−2175.06	−1384.05	6.40	287.62

and

Table A2. Additional results of experiments (a), (b), and (c).

	Drawdown			Trades
	a	b	c	a	b	c
AUDUSD	98.79	52.90	48.82	266	59	40
EURGBP	91.62	66.82	67.88	242	162	141
EURUSD	82.51	47.95	42.18	243	81	60
GBPUSD	90.03	55.78	59.42	248	152	133
USDCHF	94.56	73.40	72.92	254	83	64
USDJPY	96.80	73.36	79.95	240	86	69
XAUUSD	27.32	16.40	16.04	228	119	99
OIL	99.60	98.43	98.07	188	80	59
BTCUSD	14.45	9.44	9.50	221	84	64

and Figure 6 and Figure 7.

It can be concluded that holding open positions over the weekends helps cut one’s losses, but it also takes away a proportion of the profits for all the examined assets. Figure 6 makes clear that the net profits in most cases are diminished and Figure 7 shows the usually higher drawdown when holding positions open over the weekend. Also, using the default parameters almost always results in losses. Because of differences in contract sizes, trading hours, variability, etc., the XAUUSD, OIL, and BTCUSD show different numbers compared with the FOREX pairs (a behavior that also presents itself to the rest of the experiments) but, in the relativity of the experiments’ comparisons, their numbers still support the conclusions. The Net Profits in Table A1 and, by extension, for all later experiments, are a result of the parameter selection described in Section 2.4.2., which is a posteriori process. The actual amount of returns and the profitability of the MACD Expert Advisor are not something we actually concern ourselves with in this research, but rather how these returns change by adding each Take Profit and Stop Loss strategy.

From now on, in our experiments, we will be using our selected parameters for each asset and open positions will be closed for the weekends.

3.2. Fast Take Profit Signal and Signals’ Hierarchy

Next, we compared the (b) simple MACD Expert Advisor with the (d) MACD Expert Advisor, with the addition of a faster take profit signal, as described in Section 2.3.2. The determined value of the divisor N of the Fast Signal period was set as follows: N = {2,3,4}. With N = 1, the (d) Expert Advisor effectively becomes the same as (b), as the Fast Signal line becomes identical to the Signal line. Their results can be seen in

Table A3. Results of experiment (d) for various values of N.

	Gross Profits				Gross Losses				Net Profits
	b (N = 1)	d, N = 2	d, N = 3	d, N = 4	b (N = 1)	d, N = 2	d, N = 3	d, N = 4	b (N = 1)	d, N = 2	d, N = 3	d, N = 4
AUDUSD	37,294	25,474	24,725	544	−30,278	−25,896	−24,269	−29	7015	−422	456	515
EURGBP	54,415	59,520	55,503	55,503	−55,194	−60,383	−58,596	−58,596	−778	−863	−3094	−3094
EURUSD	36,116	37,642	38,389	40,268	−31,767	−32,361	−33,461	−37,011	4349	5281	4929	3257
GBPUSD	47,999	48,220	54,566	47,588	−45,679	−47,279	−54,533	−49,227	2320	941	33	−1639
USDCHF	27,829	20,634	18,821	20,256	−24,067	−22,316	−21,671	−22,752	3762	−1683	−2850	−2496
USDJPY	27,056	21,233	26,475	26,142	−22,927	−23,304	−26,338	−27,942	4129	−2072	137	−1799
XAUUSD	9115	9048	9864	9928	−8809	−8618	−8476	−8912	307	430	1388	1016
OIL	81,593	71,421	51,236	51,994	−73,269	−66,204	−56,279	−58,578	8323	5217	−5043	−6584
BTCUSD	2377	2247	2284	2265	−2371	−2554	−2586	−2576	6	−307	−302	−311

and

Table A4. Additional results of experiment (d) for various values of N.

	Drawdown				Trades
	b (N = 1)	d, N = 2	d, N = 3	d, N = 4	b (N = 1)	d, N = 2	d, N = 3	d, N = 4
AUDUSD	59.84	73.92	69.72	65.13	59	67	68	74
EURGBP	70.03	73.49	76.14	76.14	162	186	210	210
EURUSD	55.44	57.48	56.33	57.82	81	88	96	104
GBPUSD	52.13	63.16	58.47	61.14	152	171	192	216
USDCHF	74.98	75.60	78.35	75.70	83	101	112	118
USDJPY	77.06	83.04	78.24	78.21	86	101	104	112
XAUUSD	18.73	13.47	10.78	11.96	119	136	152	161
OIL	98.80	97.80	98.14	97.35	80	87	93	99
BTCUSD	11.30	13.81	13.42	12.84	84	89	96	105

and Figure 8 and Figure 9.

The simple MACD yields better results in most cases, both in terms of net profits and drawdown, especially on Forex pairs. Even when assets which are traded using the MACD do not yield the most profitable results, it is postulated that the MACD ranks second after a neck-and-neck round, with a fast Take Profit signal of N = 2.

Next, we compared the (b) simple MACD Expert Advisor with the (e) MACD Expert Advisor that only opens new positions when the hierarchy of the MACD and Signal lines is right, as described in Section 2.3.3. The divisor N of the Fast Signal period assumed values of N = {2,3,4}. With N = 1, the e) Expert Advisor becomes the same as (b). Their results can be seen in

Table A5. Results of experiment (e) for various values of N.

	Gross Profits				Gross Losses				Net Profits
	b (N = 1)	e, N = 2	e, N = 3	e, N = 4	b (N = 1)	e, N = 2	e, N = 3	e, N = 4	b (N = 1)	e, N = 2	e, N = 3	e, N = 4
AUDUSD	37,294	24,838	26,666	29,074	−30,278	−23,346	−22,296	−26,120	7015	1492	4370	2954
EURGBP	54,415	36,836	44,974	44,974	−55,194	−41,263	−49,168	−49,168	−778	−4428	−4194	−4194
EURUSD	36,116	28,172	35,252	37,813	−31,767	−25,534	−30,184	−33,621	4349	2638	5068	4192
GBPUSD	47,999	39,274	49,657	51,052	−45,679	−40,010	−48,985	−51,998	2320	−736	671	−946
USDCHF	27,829	15,949	16,941	17,136	−24,067	−20,830	−21,086	−21,171	3762	−4880	−4146	−4035
USDJPY	27,056	17,328	23,076	25,002	−22,927	−20,258	−24,040	−27,339	4129	−2929	−964	−2338
XAUUSD	9115	7220	7882	8678	−8809	−7950	−7623	−8112	307	−730	259	566
OIL	81,593	84,182	74,125	59,685	−73,269	−72,111	−72,253	−65,487	8323	12,071	1871	−5802
BTCUSD	2377	2085	2208	2179	−2371	−2171	−2476	−2512	6	−86	−267	−333

and

Table A6. Additional results of experiment (e) for various values of N.

	Drawdown				Trades
	b (N = 1)	e, N = 2	e, N = 3	e, N = 4	b (N = 1)	e, N = 2	e, N = 3	e, N = 4
AUDUSD	59.84	68.68	60.71	57.72	59	63	65	71
EURGBP	70.03	72.45	75.01	75.01	162	175	205	205
EURUSD	55.44	51.98	47.68	52.07	81	77	91	100
GBPUSD	52.13	62.45	57.63	63.58	152	153	178	206
USDCHF	74.98	80.71	79.28	78.96	83	97	109	115
USDJPY	77.06	84.73	79.44	77.03	86	92	97	105
XAUUSD	18.73	22.35	19.39	15.90	119	124	143	153
OIL	98.80	95.67	95.32	97.05	80	76	85	91
BTCUSD	11.30	12.00	12.85	13.20	84	80	91	102

and Figure 10 and Figure 11.

Again, it is evident that the simple MACD Expert Advisor generally produces better results than the MACD, which opens positions with the hierarchy of lines.

3.3. Constant ATR Zone, Sliding ATR Zone, Sliding and Variable ATR Zone

The first Stop Loss strategy we examined was f) a MACD Expert Advisor that creates a Stop Loss zone at ±x × ATR(N) when it opens a new position and a new position prevention zone at ±y × ATR(N), after a position has to be closed due to a Stop Loss that has been triggered. We tested every combination of parameters for N:{12,24,36,48}, x:{1,2,3,4,5,6,7}, and y:{1,2,3,4}. The Net Profits for each asset for every combination of N, x, y have been outlined in Figure 12 and Drawdown in Figure 13.

The periodicity that can be seen in Figure 12 indicates that the x multiplier plays a significant role in this strategy. For small values of x (=1), net profits are diminished for all assets, while with larger values of x (5,6,7), profits are more constant and approach those of the simple MACD, as the big ATR zone does not trigger a Stop Loss very often. Values of x (2,3,4) yield the best results compared to the others. In the drawdown diagram, there also seems to be periodicity for y, with bigger values (y = 3,4) having lower drawdown.

Next, we examined g) an MACD Expert Advisor with a sliding Stop Loss zone ±x × ATR(N) as described in Section 2.3.6 and a constant new position prevention zone at ±y × ATR(N). We tested every combination of parameters for N:{12,24,36,48}, x:{1,2,3,4,5,6,7}, and y:{1,2,3,4}. The Net Profits for each asset for every combination of N, x, y are displayed in Figure 14 and Drawdown in Figure 15.

The general picture is the same as the case of (f). For small values of x, the profits are diminished, while for larger values of x, they tend to stay constant and approach the Simple MACD’s results. Additionally, large values of y tend to have lower drawdown.

Finally, we examined (h) an MACD Expert Advisor with a sliding and variable Stop Loss zone ±x × ATR(N), with a new value of ATR used at hourly intervals as described in Section 2.3.7 and a constant new position prevention zone at ±y × ATR(N). We tested every combination of parameters for N:{12,24,36,48}, x:{1,2,3,4,5,6,7}, and y:{1,2,3,4}. The Net Profits for each asset for every combination of N, x, y have been outlined in Figure 16 and Drawdown in Figure 17.

In this case, apart from the same conclusions that can be reached in the two previous tests, we can observe a clear peak in the profits in the neighborhood of (12,6,2), even when accounting for the big spikes from the OIL profits (the drawdown is also below total average in this area). This becomes more evident when we draw the diagram, Figure 18, of average profits for the (b) Simple MACD, (f) MACD with a constant ATR zone, (g) MACD with a sliding ATR zone, and (h) MACD with a sliding and variable ATR zone.

A neighborhood around 12,6,2 of MACD with sliding and variable ATR windows clearly stands out, consistently having the edge over the simple MACD, as well as the other Stop Loss strategies. Apart from some solitary peaks, the other strategies do not outperform the simple MACD system.

4. Conclusions

In the present research, we examined various Take Profit and Stop Loss strategies added to a simple MACD automated trading system used in trading 10 assets from the Forex, Metals, Energy, and Cryptocurrencies categories. In order to make the MACD parameters less important in our research, we chose parameters based on the characteristics of their neighborhoods of ±2 and used them for all our experiments.

In our research, we first of all concluded that it is generally less profitable to keep positions open during weekends. Another conclusion we reached is that Take Profit strategies based on faster take profit signals on MACD are not far better than a simple MACD strategy. We also showed that among the different Stop Loss strategies based on ATR windows, the best and safest results come from a sliding and variable ±x × ATR(N) window with period N = 12 and multiplier x = 6 after opening a position and a constant ±y × ATR(N) with period N = 12 and multiplier y = 2 after stop loss closing.

Since the MACD Indicator is used quite prevalently by a lot of traders and our results are general enough, a trader could incorporate them in their technical analysis/trading strategy for Stop Loss and Take Profit without interfering with the rest of their strategy (portfolio management, capital allocation, MACD parameter selection, etc.)