Multi-Objective Optimal Charging Method for Lithium-Ion Batteries
Abstract
:1. Introduction
2. Lithium-Ion Battery Testing and Modeling
2.1. Charging Principle and Model Selection
2.2. Parameter Identification and Verification of Battery Model
3. Multi-Objective Optimal Charging Method
3.1. Determination of the Boundary Condition of Charging Current
3.2. Establishment of Optimization Objective Function
3.3. Solution of Charging Current using a Dynamic Programming Algorithm
4. Analysis of Simulation and Experimental Results
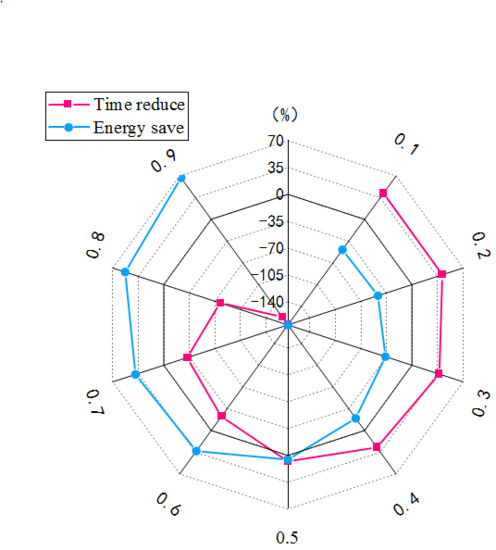
4.1. Optimization Results for Different Weighting Factors
4.2. Analysis of the Weighting Factors
4.3. Attenuation Comparison of Battery Capacity
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
| List of symbols. |
| Symbol | Significance | Symbol | Significance |
| R0 | Ohmic resistance | Maximum charging current | |
| R1 | polarization resistance | percentage of maximum charge capacity | |
| C1 | polarization capacitance | energy loss | |
| UOC | open-circuit voltage | I | Charging current |
| voltage error | W1 | energy loss of the polarization resistance | |
| actual value of the battery terminal voltage | Cap | battery rated capacity | |
| simulation value of the battery terminal voltage | η | Coulomb efficiency | |
| SOC | State of charge | charging time of each charging phase | |
| sampling time | Time reduce | ||
| charging time | Energy save | ||
| objective function | x | throughput capacity | |
| α | weighting factor | percentage of battery capacity attenuation | |
| M | compensating coefficient | relative capacity decay rate | |
| j | charging stage |
References
- Du, J.; Ouyang, M.; Chen, J. Prospects for Chinese electric vehicle technologies in 2016–2020: Ambition and rationality. Energy 2017, 120, 584–596. [Google Scholar] [CrossRef]
- Pattipati, B.; Sankavaram, C.; Pattipati, K. System Identification and Estimation Framework for Pivotal Automotive Battery Management System Characteristics. IEEE Trans. Syst. Man Cybern. Part C 2011, 41, 869–884. [Google Scholar] [CrossRef]
- Xiong, R.; Zhang, Y.; He, H.; Zhou, X.; Pecht, M.G. A double-scale, particle-filtering, energy state prediction algorithm for lithium-ion batteries. IEEE Trans. Ind. Electron. 2017, PP, 1. [Google Scholar] [CrossRef]
- Sun, X.; Yamamoto, T.; Morikawa, T. Charge timing choice behavior of battery electric vehicle users. Transp. Res. Part D 2015, 37, 97–107. [Google Scholar] [CrossRef]
- Du, J.; Chen, J.; Song, Z.; Ouyang, M. Design method of a power management strategy for variable battery capacities range-extended electric vehicles to improve energy efficiency and cost-effectiveness. Energy 2017, 121, 32–42. [Google Scholar] [CrossRef]
- Wang, J.; Liu, P.; Hicks-Garner, J.; Sherman, E.; Soukiazian, S.; Verbrugge, M.; Tataria, H.; Musser, J.; Finamore, P. Cycle-life model for graphite-LiFePO4 cells. J. Power Sources 2011, 196, 3942–3948. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, J.; Gao, Y.; Zhang, W.; Liu, Q. Charging optimization in lithium-ion batteries based on temperature rise and charge time. Appl. Energy 2017, 194, 569–577. [Google Scholar] [CrossRef]
- Nafisi, H.; Askarian Abyaneh, H.; Abedi, M. Energy loss minimization using PHEVs as distributed active and reactive power resources: A convex quadratic local optimal solution. Int. Trans. Electr. Energy Syst. 2016, 26, 1287–1302. [Google Scholar] [CrossRef]
- Du, J.; Ouyang, D. Progress of Chinese electric vehicles industrialization in 2015: A review. Appl. Energy 2017, 188, 529–546. [Google Scholar] [CrossRef]
- Han, X.; Ouyang, M.; Lu, L.; Li, J. A comparative study of commercial lithium ion battery cycle life in electric vehicle: Capacity loss estimation. J. Power Sources 2014, 268, 658–669. [Google Scholar] [CrossRef]
- Ikeya, T.; Sawada, N.; Murakami, J.; Kobayashi, K.; Hattori, M.; Murotani, N.; Ujiie, S.; Kajiyama, K.; Nasu, H.; Narisoko, H.; et al. Multi-step constant-current charging method for an electric vehicle nickel/metal hydride battery with high-energy efficiency and long cycle life. J. Power Sources 2002, 105, 6–12. [Google Scholar] [CrossRef]
- Vo, T.T.; Chen, X.; Shen, W.; Kapoor, A. New charging strategy for lithium-ion batteries based on the integration of Taguchi method and state of charge estimation. J. Power Sources 2015, 273, 413–422. [Google Scholar] [CrossRef]
- Notten, P.H.L.; Veld, J.H.G.O.; Beek, J.R.G.V. Boostcharging Li-ion batteries: A challenging new charging concept. J. Power Sources 2005, 145, 89–94. [Google Scholar] [CrossRef]
- An, S.J.; Li, J.; Du, Z.; Daniel, C.; Wood, D.L. Fast formation cycling for lithium ion batteries. J. Power Sources 2017, 342, 846–852. [Google Scholar] [CrossRef]
- An, S.J.; Li, J.; Daniel, C.; Mohanty, D.; Nagpure, S.; Wood, D.L. The state of understanding of the lithium-ion-battery graphite solid electrolyte interphase (SEI) and its relationship to formation cycling. CARBON 2016, 105, 52–76. [Google Scholar] [CrossRef]
- Li, J.; Du, Z.; Ruther, R.E.; AN, S.J.; David, L.A.; Hays, K.; Wood, M.; Phillip, N.D.; Sheng, Y.; Mao, C.; et al. Toward Low-Cost, High-Energy Density, and High-Power Density Lithium-Ion Batteries. JOM-US 2017, 69, 1484–1496. [Google Scholar] [CrossRef]
- James, M.; Grummett, J.; Rowan, M.; Newman, J. Application of pulse charging techniques to submarine lead-acid batteries. J. Power Sources 2006, 62, 878–883. [Google Scholar] [CrossRef]
- Chen, L.R. Design of Duty-Varied Voltage Pulse Charger for Improving Li-Ion Battery-Charging Response. IEEE Trans. Ind. Electron. 2012, 56, 480–487. [Google Scholar] [CrossRef]
- Kalla, U.K.; Suthar, R.; Singh, B.; Sharma, K.; Singhal, J. Generalized electronic controller for multi-pulse battery charging systems. In Proceedings of the 6th IEEE International Conference on Power Systems, New Delhi, India, 4–6 March 2016. [Google Scholar]
- Savoye, F.; Venet, P.; Millet, M.; Groot, J. Impact of Periodic Current Pulses on Li-Ion Battery Performance. IEEE Trans. Ind. Electron. 2012, 59, 3481–3488. [Google Scholar] [CrossRef]
- Guo, Z.; Liaw, B.Y.; Qiu, X.; Gao, L.; Zhang, C. Optimal charging method for lithium ion batteries using a universal voltage protocol accommodating aging. J. Power Sources 2015, 274, 957–964. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H.; Sun, F. Charging time and loss optimization for LiNMC and LiFePO4 batteries based on equivalent circuit models. J. Power Sources 2013, 239, 449–457. [Google Scholar] [CrossRef]
- Abdollahi, A.; Han, X.; Avvari, G.V.; Raghunathan, N.; Balasingam, B.; Pattipati, K.R.; Bar-Shalom, Y. Optimal battery charging, Part I: Minimizing time-to-charge, energy loss, and temperature rise for OCV-resistance battery model. J. Power Sources 2016, 303, 388–398. [Google Scholar] [CrossRef]
- Liu, W.; Wu, C.; He, Z.; Sun, X.; Yang, G. A Multi—Stage Constant Current Charging Method Considering Internal Energy Loss and Charging Speed of Lithium Batteries. Trans. China Electrotech. Soc. 2017, 32, 112–120. [Google Scholar]
- He, H.; Xiong, R.; Guo, H.; Li, S. Comparison study on the battery models used for the energy management of batteries in electric vehicles. Energy Convers Manag. 2012, 64, 113–121. [Google Scholar] [CrossRef]
- Sun, F.; Xiong, R.; He, H. A systematic state-of-charge estimation framework for multi-cell battery pack in electric vehicles using bias correction technique. Appl. Energy 2016, 162, 1399–1409. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Xiong, R.; Yu, Q.; Wang, L.Y.; Lin, C. A novel method to obtain the open circuit voltage for the state of charge of lithium ion batteries in electric vehicles by using H infinity filter. Appl. Energy 2017. [Google Scholar] [CrossRef]
- Tsang, K.M.; Sun, L.; Chan, W.L. Identification and modelling of Lithium ion battery. Energy Convers Manag. 2010, 51, 2857–2862. [Google Scholar] [CrossRef]
- Zahid, T.; Li, W. A Comparative Study Based on the Least Square Parameter Identification Method for State of Charge Estimation of a LiFePO4 Battery Pack Using Three Model-Based Algorithms for Electric Vehicles. Energies 2016, 9, 720. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, C.; Xiong, R.; Zhou, W. Study on the Optimal Charging Strategy for Lithium-Ion Batteries Used in Electric Vehicles. Energies 2014, 7, 6783–6797. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, M.; Yang, D. Investigation of the polarization effect in lithium iron phosphate battery for electric vehicles. In Proceedings of the 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 31 August–3 September 2014. [Google Scholar]
- Groot, J.; Swierczynski, M.; Stan, A.I.; Kær, S.K. On the complex ageing characteristics of high-power LiFePO 4/graphite battery cells cycled with high charge and discharge currents. J. Power Sources 2015, 286, 475–487. [Google Scholar] [CrossRef]
- Xiong, R.; Tian, J.; Mu, H.; Wang, C. A systematic model-based degradation behavior recognition and health monitoring method for lithium-ion batteries. Appl. Energy 2017. [Google Scholar] [CrossRef]
- Gao, Y.; Jiang, J.; Zhang, C.; Zhang, W.; Ma, Z. Lithium-ion battery aging mechanisms and life model under different charging stresses. J. Power Sources 2017, 356, 103–114. [Google Scholar] [CrossRef]
- Huang, L.; Li, T.; Liu, C.; Quan, X.; Chen, L. Synergetic interactions improve cobalt leaching from lithium cobalt oxide in microbial fuel cells. Bioresour. Technol. 2013, 128, 539–546. [Google Scholar] [CrossRef] [PubMed]













| Item | Specification |
|---|---|
| Cathode material | LiCoO2 |
| Anode material | Graphite |
| Rated capacity | 2.6 Ah |
| Maximum charging current | 1C |
| Maximum discharging current | 2C |
| Charging cut-off voltage | 4.2 V |
| Discharging cut-off voltage | 3.75 V |
| Phase variables | The charge stage is divided according to ∆SOC; each charging stage is denoted by j = 1, 2, ..., N. |
| State variables | U1,j is the over-voltage at the initial moment of the jth charging phase. |
| Decision variable | Ij is the charging current during the jth charging phase. |
| Enable decision collection | Dj(Ij) = {0 ≤ Ij ≤ Imax(∆SOC) × j} |
| State transfer equation | |
| Reward function | |
| Objective value function |
| Charging Method | Time (s) | Energy Loss (J) | ||
|---|---|---|---|---|
| Proposed charging method | Weigh-ting factor | 0.1 | 4111 | 2760 |
| 0.2 | 4119 | 2715 | ||
| 0.3 | 4433 | 2527 | ||
| 0.4 | 5143 | 2216 | ||
| 0.5 | 6534 | 1752 | ||
| 0.6 | 8670 | 1239 | ||
| 0.7 | 9330 | 1146 | ||
| 0.8 | 12,510 | 871 | ||
| 0.9 | 18,180 | 615 | ||
| CCCV | 7076 | 1853 | ||
| Charge-Discharge Rate | 0.5C | 0.8C | 1C |
|---|---|---|---|
| 0.0121 | 0.0116 | 0.0141 | |
| 1.152 | 1.183 | 1.17 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Shi, W.; Du, J. Multi-Objective Optimal Charging Method for Lithium-Ion Batteries. Energies 2017, 10, 1271. https://doi.org/10.3390/en10091271
Wu X, Shi W, Du J. Multi-Objective Optimal Charging Method for Lithium-Ion Batteries. Energies. 2017; 10(9):1271. https://doi.org/10.3390/en10091271
Chicago/Turabian StyleWu, Xiaogang, Wenwen Shi, and Jiuyu Du. 2017. "Multi-Objective Optimal Charging Method for Lithium-Ion Batteries" Energies 10, no. 9: 1271. https://doi.org/10.3390/en10091271
APA StyleWu, X., Shi, W., & Du, J. (2017). Multi-Objective Optimal Charging Method for Lithium-Ion Batteries. Energies, 10(9), 1271. https://doi.org/10.3390/en10091271