1. Introduction
Apart from improving the in-cylinder design technology and favorable internal engine combustion, the exhaust gas flow increasingly gains importance in the context of exhaust after-treatment as the emission regulations are becoming more and more stringent. The injection of urea–water solution (UWS) commercially known as adBlue
® inside the exhaust port of automotive engines is one of the promising methods. Once UWS is sprayed inside the hot exhaust, the heat and mass transfer process occurs between the UWS droplets and the hot gas leaving urea that experiences thermal decomposition to form ammonia (NH
3). The gaseous NH
3 then reacts with NO
x (nitrogen oxides) and converts into harmless compound that can be finally released into the environment. The reaction and conversion efficiency mostly depends upon the evaporation and subsequent mixing into the exhaust gas. The evaporation dynamic is largely dependent on the nozzle flow properties. In most cases, complete evaporation and thermal decomposition of urea cannot be accomplished in the gas phase and UWS droplets are then deposited on the system walls leading to a reduction of the NO
x conversion efficiency of the selective catalytic reduction (SCR) system. Therefore, the SCR process requires precise control of the ammonia injection rate. An insufficient injection may result in an unacceptably low NO
x conversion. An injection rate that is too high results in the release of undesirable ammonia into the atmosphere known as ammonia-slip. This increases at higher NH
3/NO
x ratios. Due to this reason, designing an efficient reactor for such a catalytic process is a challenging task that requires a careful consideration of various physical phenomena involved during the catalytic process, such as exhaust gas flow, UWS spray dynamics, evaporation, thermal decomposition, and chemical reaction (e.g., [
1,
2]).
In this respect, extensive research and development activities are going on in both experimental and numerical areas to improve the performance of SCR systems. A recent review of the state-of-the-art technologies of selective catalytic reduction of NO
x from diesel engine exhaust can be found in [
3]. In particular, computational fluid dynamics (CFD) modeling and simulations have become established techniques to carry out detailed analysis of individual ongoing processes in SCR systems and subsequently to perform design optimization and modification in catalytic chamber. It turns out that a comprehensive CFD analysis requires a complete mathematical description of all the relevant processes involved right from the engine exhaust to the final release into the ambient as mentioned above [
4,
5,
6,
7,
8,
9,
10,
11,
12,
13].
Regarding the evaporation dynamics of UWS, two different scenarios may happen for the urea depending on the rapidity of the water evaporation [
8]. When the droplet size is small and/or the vaporization of water is slow, the concentration of urea throughout the droplet increases uniformly, which finally leads to the formation of a solid particle. However, when a rapid water vaporization occurs on the droplet surface, the urea concentration increases at the droplet surface, which builds up a urea shell around the droplet. This may lead to the boiling of water inside the urea shell and even to the explosion and fragmentation of the droplet as it has been observed experimentally. In fact, the droplet sizes are relatively large (2.4–3.0 mm) in the experiments carried out by Musa et al. [
14] who reported about extreme behavior of urea solid-crust formation, subsequent evaporation and entrapment of gaseous phase, which ultimately explode the droplets. Such a behavior can be interpreted as a combined effect of droplet heating, evaporation rate, segregation of urea composition at the droplet surface, which ultimately results in solidification of urea and formation of solid crust at the droplet surface and micro-explosion of droplets. In [
14], the authors concluded that this behavior is predominant for larger droplets due to longer evaporation time-scale.
Focusing on the numerical modeling, the adBlue droplet depletion can be modeled by three different scenarios [
2,
5,
6,
7,
9,
10,
15]: an overall evaporation process, an Arrhenius expression, or a conversion efficiency factor. In particular, a two-stage model is suggested in [
5,
6], in which it is assumed that urea decays after water is evaporated completely, while, in [
2,
12], the urea decomposition is modeled as a heat transfer limited process at a constant temperature of 152 °C. In [
7,
9], the UWS depletion is not separated in two distinct and consecutive processes, rather it is described by a multicomponent evaporation model. Thereby, the influence of various body forces on the overall droplet dynamics has been investigated, especially in [
2]. The reported CFD analysis showed that the drag and gravity forces only are important to be taken into account.
To describe the urea decomposition, the ways of heat reaction are provided [
16] play a great role in the overall mass transfer dynamics. The first way (W1) consists of an evaporation of molten/solid urea to the gaseous urea, which decomposes in the gas phase in ammonia and isocyanic acid (HNCO). The second (W2) models the urea depletion as an overall evaporation model that includes both the enthalpy of evaporation and that of the reaction in the gaseous urea. The third (W3) considers a direct decomposition from molten/solid urea to gaseous ammonia and isocyanic acid. In most contributions dealing with a single UWS droplet, e.g., [
5,
6,
12], a detailed analysis was performed. The evaporation model used usually consisted of a random mixing (RM) or a diffusion limit (DL) model for the liquid phase description and in a film based model for the gas phase. It was found out that the RM model could provide a good compromise between accuracy and simulation time. However, it should be noted that the heat/mass diffusion resistance within the droplet is zero for the RM approach, making the model capable of providing reasonable results only for slow evaporation processes in situations where the heat conduction and diffusion within the droplet do not affect significantly the internal concentration and temperature distribution [
17].
With respect to multi-component evaporation approaches, Sazhin et al. [
18,
19] recently reviewed the state-of-the-art evaporation model for hydrocarbon fuel droplets. For adBlue applications, ref. [
4,
8,
9] extend either the Sirignano’s model or the Renksizbulut et al. [
20] evaporation formulation, and mostly assume the droplet surface to be equal to the mean droplet temperature. For the liquid phase analysis, the RM model is favored. In [
4], two possible approaches (multi-component droplet and a wet-solid particle) for the representation of UWS in a CFD simulation have been evaluated. It was concluded that the wet-solid approach provides greater accuracy. In all these studies, the diffusion of species that plays a determinant role in evaporation dynamics was widely described relying on a prescribed correlation, among them the Wilke et al. formulation [
21]. While [
8] employed the Hirschfelder law instead of the Fick’s ansatz, the impact of these diffusion coefficient correlations on adBlue depletion has not yet been numerically addressed. Furthermore, in most studies, material properties in the film are evaluated usually using the 1/3 film rule and the Herning and Zipperer model as the mixing rule [
2,
7]. The effect of other film rules has not yet been evaluated on evaporation process predictions in SCR systems.
The objective of the present paper is therefore fourfold. First, a reliable multi-component evaporation model that includes a reliable binary diffusion coefficient will be developed for the first time in the Eulerian–Lagrangian CFD framework to account properly for the distinct evaporation regimes of adBlue droplets under various operating conditions. It is based on a 1D heat and mass transport equation along the droplet radius to describe the droplet heating and species diffusion inside the droplet, and on a film modelling approach according to [
22,
23] to capture the droplet evaporation and species mass fraction at and around the droplet surface. Second, this model will be extended for thermal decomposition of urea in the gaseous phase, where, depending on how the heat of thermal decomposition of urea is provided, different scenarios are considered. Third, since the evaporation model at and around the droplet surface is based on a film approach, how the material properties in the gas film along with the minimum and maximum temperatures expected at the drop surface are evaluated and influences the process results will be investigated. Fourth, the effect of ambient temperature as well as the impact of gravity on the UWS droplet depletion will be pointed out. The prediction capability of the model variants will be assessed by comparing the achieved results to each other and with experimental data. Since the droplet sizes in actual SCR scenarios are much smaller (droplet size 20–200 μm), the available experimental data by Wang et al. [
24], who considered relatively smaller droplet size among other experiments [
14,
25,
26], will be considered for model validation.
In the next section, the multicomponent evaporation modeling is provided. Thereby, a description of various binary diffusion coefficients to be used within the formulated evaporation model is outlined. To complete this section, various scenarios for thermal decompositions are introduced. In
Section 3, the numerical configurations for the respective experiments are presented. The achieved results are reported and discussed in
Section 4 in terms of model validation and various sensitivity analysis with respect to diffusion coefficient correlations, scenarios for thermal decomposition and gas film rule. The last section is devoted to conclusions.
6. Conclusions
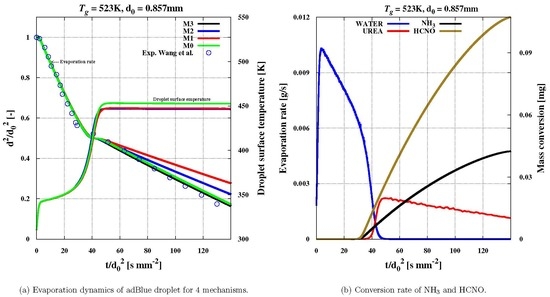
In this work, various scenarios for thermal decomposition have been investigated and assessed under SCR operating conditions relying on an appropriate multi-component evaporation model that includes a reliable binary diffusion coefficient. Such a model has been designed for the first time in the Eulerian–Lagrangian CFD framework to account properly for the distinct evaporation regimes of adBlue droplets under various operating conditions. First, the effect of diffusion coefficient correlations on the droplet thermal dynamics has been especially pointed out. It turned out that satisfactory agreement between experiment and numerical predictions was achieved for a wide range of operating temperatures by using the correlations by “Wilke and Lee” for urea and by Fuller et al. for water. The results are especially sensitive to gravity effect.
This model has been extended for thermal decomposition of urea in the gaseous phase. Depending on how the heat of thermal decomposition of urea is provided, four scenarios have been considered. The predictions of the resulting model variants have been assessed in terms of droplet evaporation rate, water and urea mass fraction inside and outside the droplet, conversion rate of isocyanic acid and ammonia as well as of droplet temperature evolution, whereby available experimental data by Wang et al. [
24] have been used for validation.
For the case of single adBlue droplet investigated in the present work, the following conclusions can be drawn:
Two evaporation regimes of urea have been observed as usual, while four stages for the thermal droplet evolution and three for the urea mass fraction inside the droplet have been pointed out.
The mass transfer rate for water is only influenced by the gas phase temperature, but not by the scenario mechanisms of thermal decomposition of urea. The urea mass transfer is significantly influenced by both ambient temperatures and reaction mechanisms. The total converted mass of NH
3 and HNCO is comparable in the mechanisms implying gas reaction, “M2” and “M3”, while a noticeable delay in the case “M2” owing to lower urea evaporation rate is initially observed. The conversions are considerably small for low gas phase temperature. In particular, at higher temperature, the simulated results with “M3”, which includes the scenario “M0” for evaporation (see
Table 7) compared well against experiments.
The impact of material properties evaluation has been highlighted: the “1/3” film rule provides acceptable results compared to the zero-film rule, even though the difference in overall prediction is very small.
Under natural convection operating conditions, the suitable model should include the effect of gravity that has been found to be significant.
The model set “M3” together with the “1/3” film rule and the gravity effect emerges as the best scenario for thermal decomposition below 600 K.
Above this value, some deviations to experiments have been observed due probably to the radiation which can be significant. This effect has not been considered in the heat transfer description in this work.
At low gas temperature, crystallization or solidification of urea can be observed due to its higher sublimation temperature. However, in SCR context, urea particle solidification should be avoided as it blocks the SCR circuit. In the context of numerical simulation, it is therefore of great interest to include the formation of solid particles together with deposition processes in a complete modeling. This requires extra effort that is not addressed here. This is left for future work.