Development of a Multi-Well Pairing System for Groundwater Heat Pump Systems
Abstract
:1. Introduction
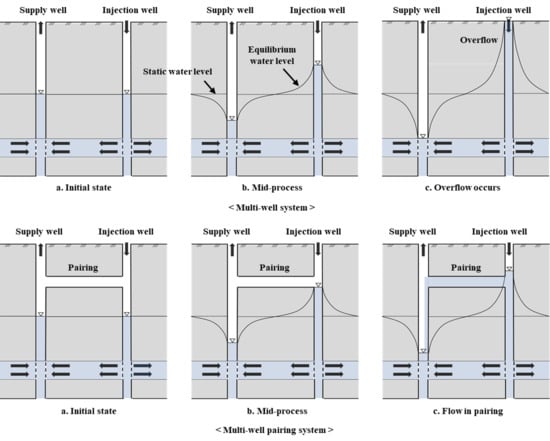
2. Summary of the Developed System
3. Real-Scale Experiment
3.1. The Experimental Site and the Analysis of Hydro-Geological Characteristics of Site
3.2. Experiment Overview
3.3. Calculation Method of System Performance
3.4. Experimental Results
4. Multi-Well Pairing Heat Exchange Model
4.1. Numerical Multi-Well Pairing Model
4.2. Analysis Method of Spill-Way
4.3. Comparison of Simulation Results and Experimental Measures
5. Case Study by Simulation
5.1. Case Condition
5.2. Results
6. Conclusions
- (1)
- The cooling and heating performance of the multi-well pairing system was compared to that of a SCW system under identical load conditions in a field-scale experiment. The cooling performance of the multi-well pairing system was 29% better than that of the SCW system, while its heating performance was 10% lower than that of the SCW system. Total power consumption in the multi-well pairing system for heating and cooling was 4% lower than in the SCW system. When annual operating costs are considered, the multi-well pairing system can be more economical than a SCW system. However, the field experiment only lasted for 18 days, therefore, data from long-term operation of the multi-well pairing system should be analyzed to assess the reliability of these results.
- (2)
- The numerical simulation was conducted to analyze the effect of hydraulic conductivity and pumping rate conditions on groundwater level at the injection well. The results of the numerical simulation showed that the impact of hydraulic conductivity on groundwater level was greater than that of pumping rate. Overflow of the injection well did not occur when the hydraulic conductivity equaled or exceeded 4 × 10−7 m/s. We consider sustainable operation of the multi-well system to be possible under these conditions.
- (3)
- At a hydraulic conductivity of 2 × 10−7 m/s without pairing, the groundwater level rose to 18.71 m at the injection well, resulting in overflow. In contrast, the multi-well pairing system raised the groundwater level to just −3.14 m. Based on the simulation results, pairing installation made sustainable operation possible even under conditions of low hydraulic conductivity. The groundwater level at the supply well was increased by pairing installation. Pairing installation is therefore expected to reduce power consumption by the supply well pump. However, the heat source temperature changes when groundwater moves from the injection well to the supply well via the spill-way. Therefore, heat source temperature and groundwater level should be considered simultaneously for the establishment of a pairing system design method.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Hahn, J.-S.; Han, H.-S.; Hahn, C. Geothermal Energy; Hanrimwon: Seoul, Korea, 2010; pp. 1–43. ISBN 978-899-351-221-2. [Google Scholar]
- Rafferty, K.D. Design issues in commercial open-loop heat pump systems. ASHRAE Trans. 2000, 114, 6–10. [Google Scholar]
- Kwon, K.-S.; Lee, J.-Y.; Mok, J.-K. Update of current on ground source heat pumps in Korea (2008–2011). J. Geol. Soc. Korea 2012, 48, 193–199. [Google Scholar]
- Zhou, X.; Gao, Q.; Chen, X.; Yu, M.; Zhao, X. Numerically simulating the thermal behaviors in groundwater wells of groundwater heat pump. Energy 2013, 61, 240–247. [Google Scholar] [CrossRef]
- Lo Russo, S.; Taddia, G.; Verda, V. Development of the thermally affected zone(TAZ) around a groundwater heat pump(GWHP) system: A sensitivity analysis. Geothermics 2012, 43, 66–74. [Google Scholar] [CrossRef]
- Lo Russo, S.; Gnavi, L.; Roccia, E.; Taddia, G.; Verda, V. Groundwater Heat Pump (GWHP) system modeling and Thermal Affected Zone (TAZ) prediction reliability: Influence of temporal variations in flow discharge and injection temperature. Geothermics 2014, 51, 103–112. [Google Scholar] [CrossRef]
- Kim, J.; Nam, Y. A Numerical Study on System Performance of Groundwater Heat Pumps. Energies 2016, 9, 4. [Google Scholar] [CrossRef]
- Al-Habaibeh, A.; Atheresh, A.P.; Parker, K. Performance analysis of using mine water from an abandoned coal mine for heating of buildings using an opern loop based single shaft GSHP system. Appl. Energy 2018, 211, 393–402. [Google Scholar] [CrossRef]
- Zhen, J.; Lu, J.; Huang, G.; Zhang, H. Groundwater source heat pump application in the heating system of Tibet Plateau airport. Energy Build. 2017, 136, 33–42. [Google Scholar] [CrossRef]
- Park, B.-H.; Lee, B.-H.; Lee, K.-K. Experimental investigation of the thermal dispersion coefficient under forced groundwater flow for designing an optimal groundwater heat pump (GWHP) system. J. Hydrol. 2018, 562, 385–396. [Google Scholar] [CrossRef]
- Park, B.-H.; Bae, G.-O.; Lee, K.-K. Importance of thermal dispersivity in designing groundwater heat pump (GWHP) system: Field and numerical study. Renew. Energy 2015, 83, 270–279. [Google Scholar] [CrossRef]
- Park, Y.; Kim, N.; Lee, J.Y. Geochemical properties of groundwater affected by open loop geothermal heat pump systems in Korea. Assoc. Korea Geosci. Soc. Springer 2015, 19, 515–526. [Google Scholar] [CrossRef]
- Bae, S.; Kim, H.; Kim, H.-W.; Nam, Y. Study on the Underground Thermal Environment around Wells for a Design Method of Open-Loop Geothermal System. Trans. Korea Soc. Geotherm. Energy Eng. 2017, 13, 14–20. [Google Scholar] [CrossRef] [Green Version]
- Theis, C.V. The relation between the lowering of the piezometric surface and the rate and duration of discharge of a well using ground-water storage. Am. Soc. Civ. Eng. 1935, 2, 519–524. [Google Scholar] [CrossRef]
- Cooper, H.H.; Jacob, C.E. A generalized graphical method of evaluating formation constants and summarizing well-field history. Am. Geophys. Union Trans. 1946, 27, 526–534. [Google Scholar] [CrossRef]
- Diersch, H.-J.G. FEFLOW Reference Manual; WASY GmbH: Berlin, Germany, 2009. [Google Scholar]
- Nam, Y.; Ooka, R. Numerical simulation of ground heat and water transfer for groundwater heat pump system based on real-scale experiment. Energy Build. 2010, 42, 69–75. [Google Scholar] [CrossRef]
- Sarkar, B.K. Fluid Mechanics and Hydraulic Machines through Practice and Solved Problems; Sunil Sachdev: New Delhi, India, 1999; Chapter 6; pp. 110–121. ISBN 81-7023-977-110-064. [Google Scholar]













| Well No. | Well Depth (m) | Well Diameter (mm) | Measure Point (m) |
|---|---|---|---|
| Well 1 | 500 | 250 | 0.06 |
| Well 2 | 250 | 250 | 0.25 |
| Well 3 | 250 | 250 | 0.43 |
| Well 4 | 250 | 250 | 0.23 |
| Well 5 | 250 | 250 | 0.24 |
| Well | Pumping Rate (Q, m3/d) | Drawdown Water Level (Sw, m) | Optimal Pumping Rate (Q, m3/d) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1st | 2nd | 3rd | 4th | 5th | 1st | 2nd | 3rd | 4th | 5th | ||
| Well 1 | 150 | 200 | 250 | 300 | - | - | 7.05 | 7.48 | 7.92 | - | 300 < |
| Well 2 | 40 | 50 | 60 | 70 | - | 13.2 | 18.09 | 24.62 | 41.47 | - | 60 = |
| Well 3 | 70 | 80 | 90 | 100 | - | 10.59 | 12.7 | 15.26 | 18.09 | - | 100 < |
| Well 4 | 150 | 200 | 250 | 300 | 350 | 1.15 | 1.86 | 2.48 | 2.99 | 4.07 | 350 < |
| Well 5 | 100 | 200 | 300 | 400 | - | 0.65 | 1.1 | 1.91 | 2.64 | - | 400 < |
| Well No. | Pumping Rate (Q, m3/d) | Hydraulic Conductivity (m/s) |
|---|---|---|
| Well 1 | 300 | 2.88 × 10−6 |
| Well 2 | 50 | 5.82 × 10−8 |
| Well 3 | 90 | 5.69 × 10−6 |
| Well 4 | 300 | 6.89 × 10−6 |
| Well 5 | 400 | 5.28 × 10−6 |
| System Parts | Specifications | ||
|---|---|---|---|
| SCW | Multi-Well | ||
| Well | Number of well | 1 | 2 |
| Well diameter | 250 mm | 250 mm | |
| Depth | 500 m | 250 m | |
| Spill-way | Spill-way diameter | - | 125 mm |
| Spill-way length | - | 15 m | |
| Heat exchanger | Heat exchanger capacity | 104.6 kW | |
| Heat pump | Heating capacity | 88.2 kW | |
| Cooling capacity | 84.5 kW | ||
| Heat Storage tank | Capacity | 3.09 m3 | |
| Circulation pump | Power | 1.5 kW | |
| Submersible pump | Power | 3.7 kW | |
| Element | Condition |
|---|---|
| Building type | Library |
| Temperature set | 45 °C |
| Dead bend set | 3 °C |
| Maximum heat exchanger flow set | 432 m3/d |
| Maximum heat pump flow set | 346 m3/d |
| Maximum load flow set | 360 m3/d |
| Element | Supply Well | Injection Well |
|---|---|---|
| Groundwater Level (m) | 9.01 | 9.09 |
| Hydraulic conductivity (m/s) | 6.89 × 10−6 | 5.28 × 10−6 |
| Ground temperature (°C) | 15 | 15 |
| Thermal conductivity (W/m·K) | 2.944 | 2.944 |
| Case | Hydraulic Conductivity (10−4 m/s) | Pumping Rate (m3/Day) | Pairing (Installed/Not Installed) |
|---|---|---|---|
| Case N1 | 0.008 | 300 | Not installed |
| Case N2 | 0.008 | 400 | Not installed |
| Case N3 | 0.008 | 500 | Not installed |
| Case N4 | 0.006 | 300 | Not installed |
| Case N5 | 0.006 | 400 | Not installed |
| Case N6 | 0.006 | 500 | Not installed |
| Case N7 | 0.004 | 300 | Not installed |
| Case N8 | 0.004 | 400 | Not installed |
| Case N9 | 0.004 | 500 | Not installed |
| Case N10 | 0.002 | 300 | Not installed |
| Case N11 | 0.002 | 400 | Not installed |
| Case N12 | 0.002 | 500 | Not installed |
| Case P10 | 0.002 | 300 | Installed |
| Case P11 | 0.002 | 400 | Installed |
| Case P12 | 0.002 | 500 | Installed |
| Case | Min. GWL of Supply Well (m) | Max. GWL of Injection Well (m) | Difference in GWL between Supply and Injection Well (m) | Overflow (Occurred/Not Occurred) |
|---|---|---|---|---|
| Case N1 | −9.26 | −8.71 | 0.55 | Not occurred |
| Case N2 | −9.35 | −8.62 | 0.73 | Not occurred |
| Case N3 | −9.43 | −8.52 | 0.91 | Not occurred |
| Case N4 | −10.21 | −7.69 | 2.52 | Not occurred |
| Case N5 | −10.62 | −7.27 | 3.35 | Not occurred |
| Case N6 | −11.04 | −6.85 | 4.19 | Not occurred |
| Case N7 | −13.17 | −4.73 | 8.44 | Not occurred |
| Case N8 | −14.57 | −3.07 | 11.50 | Not occurred |
| Case N9 | −16.20 | −0.86 | 15.34 | Not occurred |
| Case N10 | −15.24 | 8.17 | 23.41 | Occurred |
| Case N11 | −15.41 | 13.32 | 28.73 | Occurred |
| Case N12 | −15.50 | 18.71 | 34.21 | Occurred |
| Case P10 | −9.00 | −3.22 | 5.78 | Not occurred |
| Case P11 | −9.00 | −3.14 | 5.86 | Not occurred |
| Case P12 | −9.06 | −3.16 | 5.90 | Not occurred |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.; Nam, Y.; Bae, S.m.; Jeoun, O. Development of a Multi-Well Pairing System for Groundwater Heat Pump Systems. Energies 2018, 11, 3485. https://doi.org/10.3390/en11123485
Kim H, Nam Y, Bae Sm, Jeoun O. Development of a Multi-Well Pairing System for Groundwater Heat Pump Systems. Energies. 2018; 11(12):3485. https://doi.org/10.3390/en11123485
Chicago/Turabian StyleKim, Hongkyo, Yujin Nam, Sang mu Bae, and Oun Jeoun. 2018. "Development of a Multi-Well Pairing System for Groundwater Heat Pump Systems" Energies 11, no. 12: 3485. https://doi.org/10.3390/en11123485
APA StyleKim, H., Nam, Y., Bae, S. m., & Jeoun, O. (2018). Development of a Multi-Well Pairing System for Groundwater Heat Pump Systems. Energies, 11(12), 3485. https://doi.org/10.3390/en11123485