Assessment of Measurement Accuracy of a Micro-PIV Technique for Quantitative Visualization of Al2O3 and MWCNT Nanofluid Flows
Abstract
:1. Introduction
2. Materials and Methods
2.1. Nanofluid Preparation
2.2. Microscopic Imaging
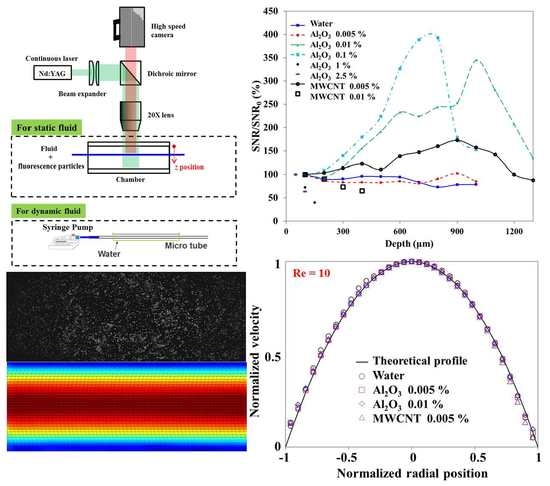
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bergles, A.E. Recent developments in enhanced heat transfer. Heat Mass Transf. 2011, 47, 1001. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Gorji-Bandpy, M.; Ganji, D.D. Review of heat transfer enhancement methods: Focus on passive methods using swirl flow devices. Renew. Sustain. Energy Rev. 2015, 49, 444–469. [Google Scholar] [CrossRef]
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Lab.: Lemont, IL, USA, 1995. [Google Scholar]
- Hwang, Y.; Lee, J.; Lee, C.; Jung, Y.; Cheong, S.; Lee, C.; Ku, B.; Jang, S. Stability and thermal conductivity characteristics of nanofluids. Thermochim. Acta 2007, 455, 70–74. [Google Scholar] [CrossRef]
- Lee, J.H.; Hwang, K.S.; Jang, S.P.; Lee, B.H.; Kim, J.H.; Choi, S.U.; Choi, C.J. Effective viscosities and thermal conductivities of aqueous nanofluids containing low volume concentrations of Al2O3 nanoparticles. Int. J. Heat Mass Transf. 2008, 51, 2651–2656. [Google Scholar] [CrossRef]
- Eastman, J.A.; Choi, S.; Li, S.; Yu, W.; Thompson, L. Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles. Appl. Phys. Lett. 2001, 78, 718–720. [Google Scholar] [CrossRef]
- Murshed, S.; Leong, K.; Yang, C. Investigations of thermal conductivity and viscosity of nanofluids. Int. J. Therm. Sci. 2008, 47, 560–568. [Google Scholar] [CrossRef]
- Buongiorno, J.; Venerus, D.C.; Prabhat, N.; McKrell, T.; Townsend, J.; Christianson, R.; Tolmachev, Y.V.; Keblinski, P.; Hu, L.; Alvarado, J.L. A benchmark study on the thermal conductivity of nanofluids. J. Appl. Phys. 2009, 106, 094312. [Google Scholar] [CrossRef] [Green Version]
- Vafaei, S.; Wen, D. Convective heat transfer of aqueous alumina nanosuspensions in a horizontal mini-channel. Heat Mass Transf. 2012, 48, 349–357. [Google Scholar] [CrossRef]
- Vafaei, S.; Purkayastha, A.; Jain, A.; Ramanath, G.; Borca-Tasciuc, T. The effect of nanoparticles on the liquid-gas surface tension of Bi2Te3nanofluids. Nanotechnology 2009, 20, 185702. [Google Scholar] [CrossRef]
- Park, H.; Lee, S.J.; Jung, S.Y. X-ray imaging analysis on behaviors of boiling bubbles in nanofluids. Int. J. Heat Mass Transf. 2019, 128, 443–449. [Google Scholar] [CrossRef]
- Park, H.; Lee, S.J.; Jung, S.Y. Effect of nanofluid formation methods on behaviors of boiling bubbles. Int. J. Heat Mass Transf. 2019, 135, 1312–1318. [Google Scholar] [CrossRef]
- Sajid, M.U.; Ali, H.M. Recent advances in application of nanofluids in heat transfer devices: A critical review. Renew. Sustain. Energy Rev. 2019, 103, 556–592. [Google Scholar] [CrossRef]
- Ebrahimi, M.; Farhadi, M.; Sedighi, K.; Akbarzade, S. Experimental investigation of force convection heat transfer in a car radiator filled with SiO2-water nanofluid. Int. J. Eng. 2014, 27, 333–340. [Google Scholar] [CrossRef]
- Ghozatloo, A.; Rashidi, A.; Shariaty-Niassar, M. Convective heat transfer enhancement of graphene nanofluids in shell and tube heat exchanger. Exp. Therm. Fluid Sci. 2013, 53, 136–141. [Google Scholar] [CrossRef]
- Selvakumar, P.; Suresh, S. Convective performance of CuO/water nanofluid in an electronic heat sink. Exp. Therm. Fluid Sci. 2012, 40, 57–63. [Google Scholar] [CrossRef]
- Xuan, Y.; Li, Q. Investigation on Convective Heat Transfer and Flow Features of Nanofluids. J. Heat Transf. 2003, 125, 151–155. [Google Scholar] [CrossRef] [Green Version]
- Khaled, A.R.A.; Vafai, K. Heat transfer enhancement through control of thermal dispersion effects. Int. J. Heat Mass Transf. 2005, 48, 2172–2185. [Google Scholar] [CrossRef]
- Nabavi, M.; Siddiqui, K. A critical review on advanced velocity measurement techniques in pulsating flows. Meas. Sci. Technol. 2010, 21, 042002. [Google Scholar] [CrossRef]
- Adrian, R.J. Particle-Imaging Techniques for Experimental Fluid Mechanics. Annu. Rev. Fluid Mech. 1991, 23, 261–304. [Google Scholar] [CrossRef]
- Santiago, J.G.; Wereley, S.T.; Meinhart, C.D.; Beebe, D.J.; Adrian, R.J. A particle image velocimetry system for microfluidics. Exp. Fluid. 1998, 25, 316–319. [Google Scholar] [CrossRef]
- Walsh, P.; Egan, V.; Walsh, E.J. Novel micro-PIV study enables a greater understanding of nanoparticle suspension flows. Microfluid. Nanofluid. 2009, 8, 837–842. [Google Scholar] [CrossRef]
- Kwek, D.; Crivoi, A.; Duan, F. Effects of Temperature and Particle Size on the Thermal Property Measurements of Al2O3−Water Nanofluids. J. Chem. Eng. Data 2010, 55, 5690–5695. [Google Scholar] [CrossRef]
- Sakamoto, M.; Kanda, Y.; Miyahara, M.; Higashitani, K. Origin of Long-Range Attractive Force between Surfaces Hydrophobized by Surfactant Adsorption. Langmuir 2002, 18, 5713–5719. [Google Scholar] [CrossRef]
- Nguyen, C.V.; Fouras, A.; Carberry, J. Improvement of measurement accuracy in micro PIV by image overlapping. Exp. Fluids 2010, 49, 701–712. [Google Scholar] [CrossRef]
- Olsen, M.; Adrian, R. Out-of-focus effects on particle image visibility and correlation in microscopic particle image velocimetry. Exp. Fluids 2000, 29, S166–S174. [Google Scholar] [CrossRef]
- Xue, Z.; Charonko, J.J.; Vlachos, P.P. Particle image velocimetry correlation signal-to-noise ratio metrics and measurement uncertainty quantification. Meas. Sci. Technol. 2014, 25, 115301. [Google Scholar] [CrossRef]
- Thielicke, W.; Stamhuis, E. PIVlab-towards user-friendly, affordable and accurate digital particle image velocimetry in MATLAB. J. Open Res. Softw. 2014, 2, e30. [Google Scholar] [CrossRef]
- Anoop, K.; Sadr, R. nPIV velocity measurement of nanofluids in the near-wall region of a microchannel. Nanoscale Res. Lett. 2012, 31, 284. [Google Scholar] [CrossRef]







| Fluids (vol%) | SNR0 | Uncertainty Lower Limit | Uncertainty Upper Limit | |
|---|---|---|---|---|
| Water | 77.3 | 0.039 | 0.298 | |
| Al2O3 | 0.005 | 209.1 | 0.018 | 0.203 |
| 0.01 | 100.2 | 0.032 | 0.269 | |
| 0.1 | 92.4 | 0.033 | 0.275 | |
| 1 | 253.7 | 0.017 | 0.192 | |
| 2.5 | 63.0 | 0.050 | 0.335 | |
| MWCNT | 0.005 | 94.8 | 0.033 | 0.273 |
| 0.01 | 102.5 | 0.035 | 0.322 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, H.; Ham, J.; Cho, H.; Jung, S.Y. Assessment of Measurement Accuracy of a Micro-PIV Technique for Quantitative Visualization of Al2O3 and MWCNT Nanofluid Flows. Energies 2019, 12, 2777. https://doi.org/10.3390/en12142777
Park H, Ham J, Cho H, Jung SY. Assessment of Measurement Accuracy of a Micro-PIV Technique for Quantitative Visualization of Al2O3 and MWCNT Nanofluid Flows. Energies. 2019; 12(14):2777. https://doi.org/10.3390/en12142777
Chicago/Turabian StylePark, Hanwook, Jeonggyun Ham, Honghyun Cho, and Sung Yong Jung. 2019. "Assessment of Measurement Accuracy of a Micro-PIV Technique for Quantitative Visualization of Al2O3 and MWCNT Nanofluid Flows" Energies 12, no. 14: 2777. https://doi.org/10.3390/en12142777
APA StylePark, H., Ham, J., Cho, H., & Jung, S. Y. (2019). Assessment of Measurement Accuracy of a Micro-PIV Technique for Quantitative Visualization of Al2O3 and MWCNT Nanofluid Flows. Energies, 12(14), 2777. https://doi.org/10.3390/en12142777