Endoreversible Trigeneration Cycle Design Based on Finite Physical Dimensions Thermodynamics
Abstract
:1. Introduction
- Equilibrium thermodynamics (ET) involves the reversible Carnot cycle and Carnot energy efficiency. Besides, they developed the methods of optimization of real cycles by using mean thermodynamic temperature, exergy, and irreversible entropy generation concepts. These additional concepts can evaluate the irreversibility of real cycles by comparison with the Carnot one. The use of the Carnot cycle does not take into account the time, respectively it has maximum–maximorum energy efficiency but zero power because it asks infinitesimal temperature differences, i.e., infinite time to fulfill the heat transfers between the working fluid and external heat reservoirs.
- Finite time thermodynamics (FTT) based on Curzon–Ahlborn–Novikov maximum power and energy efficiency at maximum power criteria. FTT considers the externally irreversible Carnot cycle that requires finite time to complete the heat transfers between the working fluid and external heat reservoirs. The main drawback of approaches based on FTT is the fact that it cannot be applied entirely for non-Carnot irreversible cycles, see for instance [1], where they concluded: “Things are not so straightforward that a simple formula may account for a variety of situations”.
- Finite physical dimensions thermodynamics (FTPD) allows various approaches based on energy/entropy, like in ET or on energy/entropy rates close to FTT. FTPD assessments are entropic approaches because they define and use the dependences between the reference entropy and the control operational parameters characterizing the external energy interactions of thermal systems. The particular influences of reference entropy variations of the working fluids are substituted with influences of operational finite dimensions control parameters, i.e., finite temperature differences, finite thermal conductance inventory of heat exchangers, and finite energy rates. The internal irreversibility of cycles can be quantified through extra irreversible entropy generation models depending on the working fluid nature and the type/geometry of thermal system. The FPDT restrictive design prerequisites of basic energy systems might consider constant reference entropy, constant heat input, constant power, or constant energy efficiency.
- Finite speed thermodynamics (FST) studies the interactions between moving solids and fluids. FST has a narrow domain of application, i.e., reciprocating thermal machines.
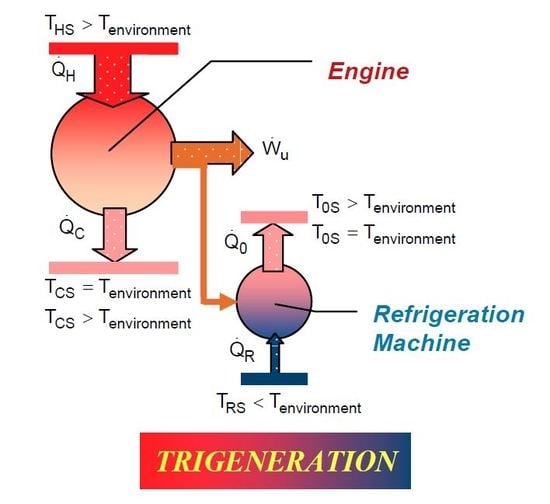
2. FPDT-Based Design Statements
- Supplying power and refrigeration rate, the summer season;
- Supplying power and heat rate by engine cycle, and refrigeration rate by reverse cycle, the winter season;
- Supplying power by engine cycle, and heat and refrigeration rates by reverse cycle, the winter season; and
- Supplying power and heat rate by engine cycle, and heat and refrigeration rates by reverse cycle, the winter season.
- TCS = Tenvironment, T0S = Tenvironment;
- TCS > Tenvironment, T0S = Tenvironment;
- TCS = Tenvironment, T0S > Tenvironment;
- TCS > Tenvironment, T0S > Tenvironment.
- Two mean log temperature differences between the working fluids and external heat sources (ΔTH–the mean log temperature difference of the heat exchanger thermally linking the engine working fluid with the engine hot heat source; and ΔTR–the mean log temperature difference of the heat exchanger thermally linking the refrigeration working fluid with the refrigeration machine cold heat source); and
- Two dimensionless thermal conductance inventory:for the engine cycle, andfor the refrigeration cycle.
3. Basic Mathematical Model
3.1. Engine
- -
- External heat reservoirs temperature ratio , and
- -
- Variable mean log temperature difference ΔTH [K], inside the heat exchanger working at the hot side of engine.
- Thermal conductance inventory:where U [kW·m−2·K−1] is the overall heat transfer coefficient and A [m2] is the heat transfer area.
- Energy balance Equations:
- Energy efficiency Equation:
- Exergy efficiency equation, related to exergy contents of :
- -
- [kg·s−1] is the mass flow rate of the working fluid through engine;
- -
- [kW] is the engine cycle input heat rate;
- -
- [K] is the mean thermodynamic temperature of the working fluid at the hot side;
- -
- [K] is, by definition, the fitting mean temperature of the hot heat source, complying with Equation (4);
- -
- [kW] is the engine cycle exhaust heat rate;
- -
- TC [K] is the mean thermodynamic temperature of the working fluid at the cold side; and
- -
- [K] is, by definition, the fitting mean temperature of the cold heat sink, complying with Equation (6).
3.2. Refrigeration Machine
- -
- The reference entropy rate of working fluid for the endoreversible reverse cycle is :The finite physical dimension control parameters are:
- -
- External heat reservoirs temperatures ratio , and
- -
- Variable mean log temperature difference ΔTC [K], inside the heat exchanger at the cold heat source of refrigeration machine.
- Thermal conductance inventory:where U [kW·m−2·K−1] is the overall heat transfer coefficient and A [m2] is the heat transfer area.
- Energy balance Equations:
- Energy efficiency Equation:
- Exergy efficiency Equation, related to exergy contents of :
- -
- [kg·s−1] is the mass flow rate of the working fluid through the refrigeration machine;
- -
- [kW] is the refrigeration heat rate;
- -
- [K] is the mean thermodynamic temperature of the working fluid at the cycle cold side;
- -
- [K] is, by definition, the fitting mean temperature of the cold heat source, complying with Equation (14);
- -
- [kW] is the absolute heat rate at the hot heat sink;
- -
- [K] is mean thermodynamic temperature of the working fluid at the cycle hot side; and
- -
- T0S is, by definition, the fitting mean temperature of the hot heat sink, complying with Equation (16).
3.3. Endoreversible Trigeneration System
- Case “a”—energy efficiency:
- Case “b”—energy efficiency:
- Case “c”—energy efficiency:
- Case “d”—energy efficiency:
4. Numerical Results
5. Design of Endoreversible Trigeneration Systems
- Imposed useful minimum power, , that implies
- Imposed consumed power by refrigeration machine, ,
- Imposed ratio of engine power to refrigeration rate, ,
- Imposed refrigeration rate, , and
- Imposed cogeneration energy efficiency, ; thus it assumes that there are existing consumers of all the useful heat rates (DHW and heating customers).
6. Discussion
- Defining the reference complete reversible trigeneration models for all possible schemes of providing imposed useful energies. This stage was well performed by considering the Carnot cycle.
- Defining the reference endoreversible trigeneration models for all possible schemes of providing imposed useful energies. This stage might be well achieved through FPDT mathematical models. These models allow the generalization of design results, not depending on the working fluid nature.
- The limitations of endoreversibility have to be assessed for cases when the reversible model cannot be applied entirely for all possible cycles, see for instance [1]. The limitations of the Carnot cycle are exceeded through mean thermodynamic temperature concepts. Thus, the Carnot model remains as the reference for all types of irreversible cycles. The comparison, reversible–irreversible, is performed through lost exergy, irreversible entropy generation, and second law efficiency concepts. The Curzon–Ahlborn–Novikov approach has limitations related to the efficiency at maximum power because it does not imply the entropy/entropy balance in its mathematical model. In this paper, the basic endoreversible trigeneration mathematical models considering all endoreversible non-Carnot cycles were generalized through the mean thermodynamic concept and the new defined mean temperature of external heat reservoirs complying with coupled energy conservation and linear heat transfer equations. These mathematical models would be the reference ones to compare reversibility–irreversibility, either by lost exergy/second law efficiency or by an overall number of internal irreversibility, see [38].
- Defining the reference models assessing the irreversibility influence. The equilibrium thermodynamics were completed through the means of thermodynamic temperature, exergy, and irreversible entropy generation concepts. The FPDT assessments might be completed either defining a single concept evaluating priori the overall internal irreversibility, see for instance the short communication [38], or making a sensitivity analysis of each operational trigeneration scheme depending on the working fluid nature and on the type of thermal system.
- Defining the optimization methods of reference reversible and irreversible cycles. The optimization methods consider either pure thermodynamic criteria, CAPEX criteria, operational costs criteria (see for instance [24]), environmental criteria (see LCA method), or improvement of a specific defined efficiency of thermal systems. The more elaborated methods combine different criteria.
- Defining the reference models for possible interconnected trigeneration grids and the evaluation of performances, energy interactions, investments, operational costs, environmental effects, preservation of natural resources.
- Defining the optimization methods for possible interconnected trigeneration grids. One good method might use MILP models, see reference [37].
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ouerdane, H.; Apertet, Y.; Goupil, C.; Lecoeur, P. Continuity and boundary conditions in thermodynamics: From Carnot’s efficiency to efficiencies at maximum power. Eur. Phys. J. Spec. Top. 2015, 224, 862. [Google Scholar] [CrossRef]
- Isa, N.M.; Tan, C.W.; Yatim, A. A comprehensive review of cogeneration system in a microgrid: A perspective from architecture and operating system. Renew. Sustain. Energy Rev. 2018, 81, 2236–2263. [Google Scholar] [CrossRef]
- Badami, M.; Gerboni, R.; Portoraro, A. Determination and assessment of indices for the energy performance of district heating with cogeneration plants. Energy 2017, 127, 697–703. [Google Scholar] [CrossRef]
- Khaliq, A.; Dincer, I. Energetic and exergetic performance analyses of a combined heat and power plant with absorption inlet cooling and evaporative aftercooling. Energy 2011, 36, 2662–2670. [Google Scholar] [CrossRef]
- Pina, E.A.; Lozano, M.A.; Serra, L.M. Optimal operation and marginal costs in simple trigeneration systems including thermal energy storage. Energy 2017, 135, 788–798. [Google Scholar] [CrossRef] [Green Version]
- Santo, D.B.D.E.; Gallo, W.L.R. Utilizing primary energy savings and exergy destruction to compare centralized thermal plants and cogeneration/trigeneration systems. Energy 2017, 120, 785–795. [Google Scholar] [CrossRef]
- Memon, A.G.; Memon, R.A. Thermodynamic analysis of a trigeneration system proposed for residential application. Energy Convers. Manag. 2017, 145, 182–203. [Google Scholar] [CrossRef]
- Mohammadi, A.; Kasaeian, A.; Pourfayaz, F.; Ahmadi, M.H. Thermodynamic analysis of a combined gas turbine, ORC cycle and absorption refrigeration for a CCHP system. Appl. Therm. Eng. 2017, 111, 397–406. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Ahmadi, M.A.; Pourfayaz, F. Thermodynamic analysis and evolutionary algorithm based on multi-objective optimization performance of actual power generating thermal cycles. Appl. Therm. Eng. 2016, 99, 996–1005. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C.; Antonopoulos, K.A. Parametric investigation and optimization of an innovative trigeneration system. Energy Convers. Manag. 2016, 127, 515–525. [Google Scholar] [CrossRef]
- Baghernejad, A.; Yaghoubi, M.; Jafarpur, K. Exergoeconomic optimization and environmental analysis of a novel solar-trigeneration system for heating, cooling and power production purpose. Sol. Energy 2016, 134, 165–179. [Google Scholar] [CrossRef]
- Ghaebi, H.; Saidi, M.; Ahmadi, P. Exergoeconomic optimization of a trigeneration system for heating, cooling and power production purpose based on TRR method and using evolutionary algorithm. Appl. Therm. Eng. 2012, 36, 113–125. [Google Scholar] [CrossRef]
- Ahmadi, P.; Dincer, I. Exergoenvironmental analysis and optimization of a cogeneration plant system using Multimodal Genetic Algorithm (MGA). Energy 2010, 35, 5161–5172. [Google Scholar] [CrossRef]
- Kanoglu, M.; Dincer, I.; Rosen, M.A. Understanding energy and exergy efficiencies for improved energy management in power plants. Energy Policy 2007, 35, 3967–3978. [Google Scholar] [CrossRef]
- Mustafa, M.F.; Nord, N.; Calay, R.K.; Mustafa, M.Y. A Hybrid Biomass Hydrothermal Gasification- Solid Oxide Fuel Cell System Combined with Improved CHP Plant for Sustainable Power Generation. Energy Procedia 2017, 112, 467–472. [Google Scholar] [CrossRef]
- Rohde, D.; Andresen, T.; Nord, N. Analysis of an integrated heating and cooling system for a building complex with focus on long–term thermal storage. Appl. Therm. Eng. 2018, 145, 791–803. [Google Scholar] [CrossRef]
- Colmenar-Santos, A.; Zarzuelo-Puch, G.; Borge-Diez, D.; García-Diéguez, C. Thermodynamic and exergoeconomic analysis of energy recovery system of biogas from a wastewater treatment plant and use in a Stirling engine. Renew. Energy 2016, 88, 171–184. [Google Scholar] [CrossRef]
- Blazqueza, C.S.; Borge-Diezb, D.; Nietoa, I.M.; Martina, A.F.; Gonzalez-Aguileraa, D. Technical optimization of the energy supply in geothermal heat pumps. Geothermics 2019, 81, 133–142. [Google Scholar] [CrossRef]
- Tereshchenko, T.; Nord, N. Implementation of CCPP for energy supply of future building stock. Appl. Energy 2015, 155, 753–765. [Google Scholar] [CrossRef] [Green Version]
- Colmenar-Santos, A.; Rosales-Asensio, E.; Borge-Diez, D.; Mur-Perez, F. Cogeneration and district heating networks: Measures to remove institutional and financial barriers that restrict their joint use in the EU-28. Energy 2015, 85, 403–414. [Google Scholar] [CrossRef]
- Colantoni, A.; Villarini, M.; Marcantonio, V.; Gallucci, F.; Cecchini, M. Performance Analysis of a Small-Scale ORC Trigeneration System Powered by the Combustion of Olive Pomace. Energies 2019, 12, 2279. [Google Scholar] [CrossRef]
- Jamaluddin, K.; Alwi, S.R.W.; Manan, Z.A.; Hamzah, K.; Klemeš, J.J. A Process Integration Method for Total Site Cooling, Heating and Power Optimisation with Trigeneration Systems. Energies 2019, 12, 1030. [Google Scholar] [CrossRef]
- Salem, R.; Bahadori-Jahromi, A.; Mylona, A.; Godfrey, P.; Cook, D. Comparison and Evaluation of the Potential Energy, Carbon Emissions, and Financial Impacts from the Incorporation of CHP and CCHP Systems in Existing UK Hotel Buildings. Energies 2018, 11, 1219. [Google Scholar] [CrossRef]
- Cozzolino, R. Thermodynamic Performance Assessment of a Novel Micro-CCHP System Based on a Low Temperature PEMFC Power Unit and a Half-Effect Li/Br Absorption Chiller. Energies 2018, 11, 315. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C. Optimization of a Solar-Driven Trigeneration System with Nanofluid-Based Parabolic Trough Collectors. Energies 2017, 10, 848. [Google Scholar] [CrossRef]
- Gopisetty, S.; Treffinger, P. Generic Combined Heat and Power (CHP) Model for the Concept Phase of Energy Planning Process. Energies 2017, 10, 11. [Google Scholar] [CrossRef]
- Piacentino, A.; Gallea, R.; Catrini, P.; Cardona, F.; Panno, D. On the Reliability of Optimization Results for Trigeneration Systems in Buildings, in the Presence of Price Uncertainties and Erroneous Load Estimation. Energies 2016, 9, 1049. [Google Scholar] [CrossRef]
- Acevedo, L.; Uche, J.; Del Almo, A.; Círez, F.; Usón, S.; Martínez, A.; Guedea, I. Dynamic Simulation of a Trigeneration Scheme for Domestic Purposes Based on Hybrid Techniques. Energies 2016, 9, 1013. [Google Scholar] [CrossRef]
- Kang, E.-C.; Lee, E.-J.; Ghorab, M.; Yang, L.; Entchev, E.; Lee, K.-S.; Lyu, N.-J. Investigation of Energy and Environmental Potentials of a Renewable Trigeneration System in a Residential Application. Energies 2016, 9, 760. [Google Scholar] [CrossRef]
- Marrasso, E.; Roselli, C.; Sasso, M.; Tariello, F. Analysis of a Hybrid Solar-Assisted Trigeneration System. Energies 2016, 9, 705. [Google Scholar] [CrossRef]
- Mathkor, R.Z.; Agnew, B.; Al-Weshahi, M.A.; Latrsh, F. Exergetic Analysis of an Integrated Tri-Generation Organic Rankine Cycle. Energies 2015, 8, 8835–8856. [Google Scholar] [CrossRef]
- Stojiljković, M.M.; Stojiljković, M.M.; Blagojević, B.D. Multi-Objective Combinatorial Optimization of Trigeneration Plants Based on Metaheuristics. Energies 2014, 7, 8554–8581. [Google Scholar] [CrossRef] [Green Version]
- Mohan, G.; Dahal, S.; Kumar, U.; Martin, A.; Kayal, H. Development of Natural Gas Fired Combined Cycle Plant for Tri-Generation of Power, Cooling and Clean Water Using Waste Heat Recovery: Techno-Economic Analysis. Energies 2014, 7, 6358–6381. [Google Scholar] [CrossRef] [Green Version]
- Feidt, M. Finite Physical Dimensions Optimal Thermodynamics 1; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Feidt, M. Finite Physical Dimensions Optimal Thermodynamics 2; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Feidt, M.; Dumitraşcu, G.; Horbaniuc, B. Sensitivity Analysis of an Endoreversible CARNOT Energy Converter Using Finite Physical Dimensions Thermodynamics, Colloque Francophone en Energie, Environnement, Economie et Thermodynamique, June 28–29, 2018; INSA: Strasbourg, France, 2018. [Google Scholar]
- Bischi, A.; Taccari, L.; Martelli, E.; Amaldi, E.; Manzolini, G.; Silva, P.; Campanari, S.; Macchi, E. A detailed MILP optimization model for combined cooling, heat and power system operation planning. Energy 2014, 74, 12–26. [Google Scholar] [CrossRef]
- Dumitrașcu, G. The way to optimize the irreversible cycles. Rev. Termotehnica 2008, 2, 18–22. [Google Scholar]





















| θHS | TCS [K] | T0S [K] | TRS [K] | Te [K] | gH and gR | ΔTH [K] | ΔTR [K] | EE | COP | |
|---|---|---|---|---|---|---|---|---|---|---|
| Case “a” | 4 | 308 | 308 | 253 | 308 | 50 ÷ 300 | 3 ÷ 10 | 0.6 | 3.5 | |
| Case “b” | 4 | 343 | 273 | 253 | 273 | 50 ÷ 300 | 3 ÷ 10 | 0.6 | 7.0 | |
| Case “c” | 4 | 273 | 343 | 253 | 273 | 50 ÷ 300 | 3 ÷ 10 | 0.6 | 2.25 | |
| Case “d” | 4 | 343 | 343 | 253 | 273 | 50 ÷ 300 | 3 ÷ 10 | 0.6 | 2.25 |
| EEE | EEcog | COP | EE | ExE | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| - | - | - | [kW] | [kW] | [kW] | [kW] | [kW] | [kW] | [kW] | [kW] | [kW] | |
| Case a | 0.6 | 1 | 3.5 | 100 | 166.67 | 66.67 | 10 | −12.86 | −2.86 | 97.14 | 0.643 | 0.794 |
| Case b | 0.6 | 1 | 7 | 100 | 166.67 | 66.67 | 10 | −11.43 | −1.43 | 98.57 | 1.051 | fb |
| Case c | 0.6 | 1 | 2.25 | 100 | 166.67 | 66.67 | 10 | −14.44 | −4.44 | 95.56 | 0.72 | fc |
| Case d | 0.6 | 1 | 2.25 | 100 | 166.67 | 66.67 | 10 | −14.44 | −4.44 | 95.56 | 1.12 | fd |
| Case “a” | Case “b” | Case “c” | Case “d” | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| θHS | 2 | 3 | 4 | 2 | 3 | 4 | 2 | 3 | 4 | 2 | 3 | 4 |
| TCS [K] | 308 | 308 | 308 | 343 | 343 | 343 | 273 | 273 | 273 | 343 | 343 | 343 |
| TRS [K] | 253 | 253 | 253 | 253 | 253 | 253 | 253 | 253 | 253 | 253 | 253 | 253 |
| T0S [K] | 308 | 308 | 308 | 273 | 273 | 273 | 343 | 343 | 343 | 343 | 343 | 343 |
| ΔTH [K] | 90.2 | 195.3 | 308 | 100.5 | 217.5 | 343 | 79.9 | 173.1 | 273 | 100.5 | 217.5 | 343 |
| ΔTC [K] | 63.8 | 112.2 | 134 | 71 | 125.5 | 171.5 | 56.5 | 99.9 | 136.5 | 71.1 | 125.5 | 171.5 |
| ΔTR [K] | 13.5 | 13.5 | 13.5 | 6.1 | 6.1 | 6.1 | 12.2 | 12.2 | 12.2 | 12.2 | 12.2 | 12.2 |
| ΔT0 [K] | 18.3 | 18.3 | 18.3 | 6.9 | 6.9 | 6.9 | 18.3 | 18.3 | 18.3 | 18.3 | 18.3 | 18.3 |
| x | 1.38 | 1.38 | 1.38 | 3.75 | 3.75 | 3.75 | 1 | 1 | 1 | 1 | 1 | 1 |
| GTE [kW/K] | 7.57 | 2.42 | 1.3 | 6.8 | 2.176 | 1.67 | 8.54 | 2.734 | 1.456 | 6.82 | 2.182 | 1.67 |
| GTR [kW/K] | 20.51 | 20.51 | 20.51 | 123.78 | 123.78 | 123.78 | 16.44 | 16.44 | 16.44 | 16.44 | 16.44 | 16.44 |
| COP | 2.76 | 2.76 | 2.76 | 7.5 | 7.5 | 7.5 | 2 | 2 | 2 | 2 | 2 | 2 |
| EEE | 0.292 | 0.421 | 0.5 | 0.292 | 0.421 | 0.5 | 0.292 | 0.421 | 0.5 | 0.292 | 0.421 | 0.5 |
| EE | 0.55 | 0.795 | 0.94 | 1.95 | 2.37 | 2.625 | 0.878 | 1.268 | 1.5 | 1.584 | 1.843 | 2.0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gheorghe, D.; Michel, F.; Aristotel, P.; Stefan, G. Endoreversible Trigeneration Cycle Design Based on Finite Physical Dimensions Thermodynamics. Energies 2019, 12, 3165. https://doi.org/10.3390/en12163165
Gheorghe D, Michel F, Aristotel P, Stefan G. Endoreversible Trigeneration Cycle Design Based on Finite Physical Dimensions Thermodynamics. Energies. 2019; 12(16):3165. https://doi.org/10.3390/en12163165
Chicago/Turabian StyleGheorghe, Dumitrascu, Feidt Michel, Popescu Aristotel, and Grigorean Stefan. 2019. "Endoreversible Trigeneration Cycle Design Based on Finite Physical Dimensions Thermodynamics" Energies 12, no. 16: 3165. https://doi.org/10.3390/en12163165
APA StyleGheorghe, D., Michel, F., Aristotel, P., & Stefan, G. (2019). Endoreversible Trigeneration Cycle Design Based on Finite Physical Dimensions Thermodynamics. Energies, 12(16), 3165. https://doi.org/10.3390/en12163165